математика. РАЗДЕЛ 2 Случайные величины doc. Определение Величина, которая в зависимости от случая может принимать те или другие числовые значения, называется случайной
 Скачать 1.49 Mb. Скачать 1.49 Mb.
|
|
Пример 2.4. Случайная величина принимает значения только на сегменте Решение. Так как p(x)=0 при 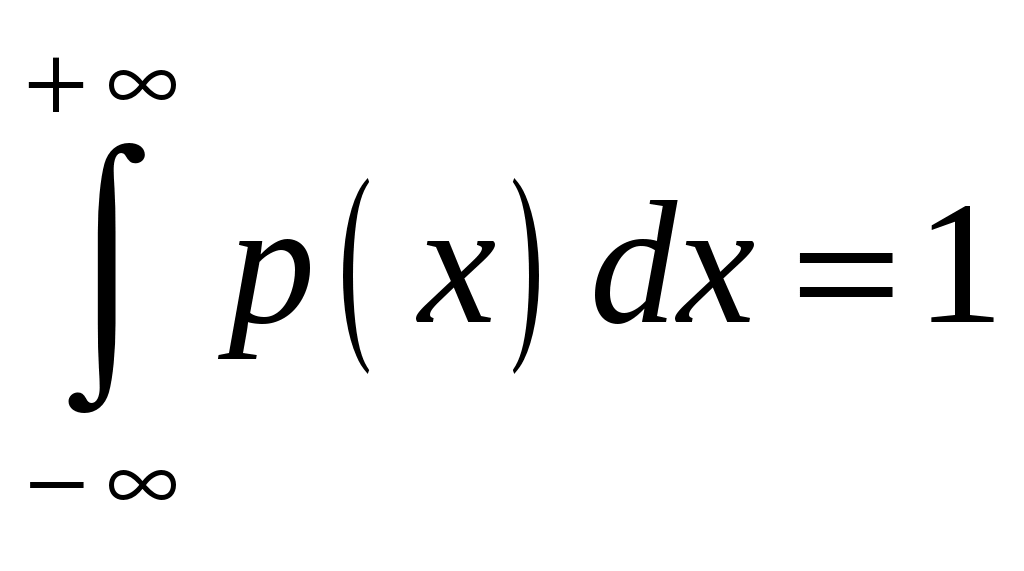 следует, что следует, что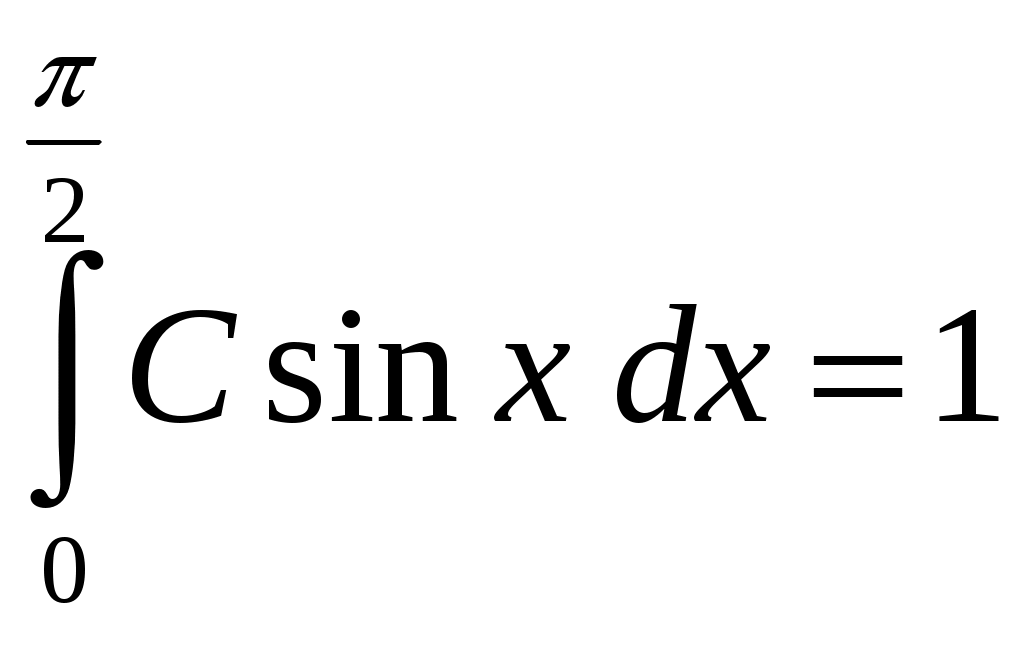 , ,Значит, C=1. Найдем числовые характеристики: математическое ожидание, дисперсию, среднее квадратическое отклонение, моду и медиану. 1) По формуле математического ожидания получаем 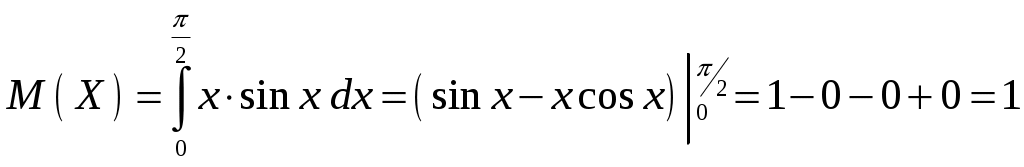 . .2) По формуле дисперсии имеем 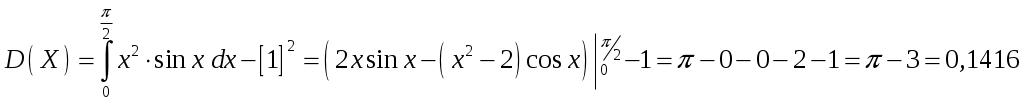 . .3) 4) Найдем моду случайной величины. Для этого сначала продифференцируем функцию плотности вероятности. В точке 5) Найдем медиану случайной величины, используя формулу 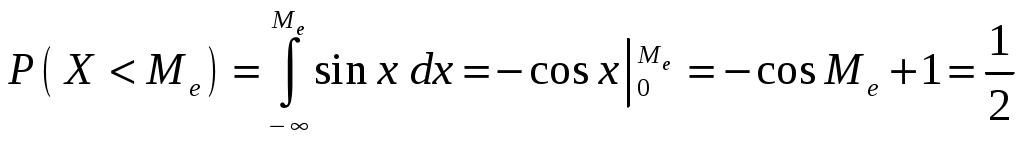 . .6) Найдем вероятность того, что случайная величина X попадет в промежуток 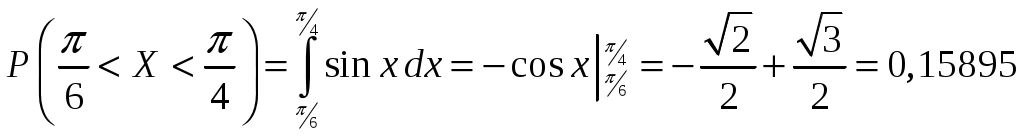 . . Законы распределения НСВ Рассмотрим часто встречающиеся законы распределения НСВ: равномерный, показательный и нормальный. 2.3.1. Равномерное распределение Непрерывная случайная величина Таким образом, плотность распределения имеет вид: 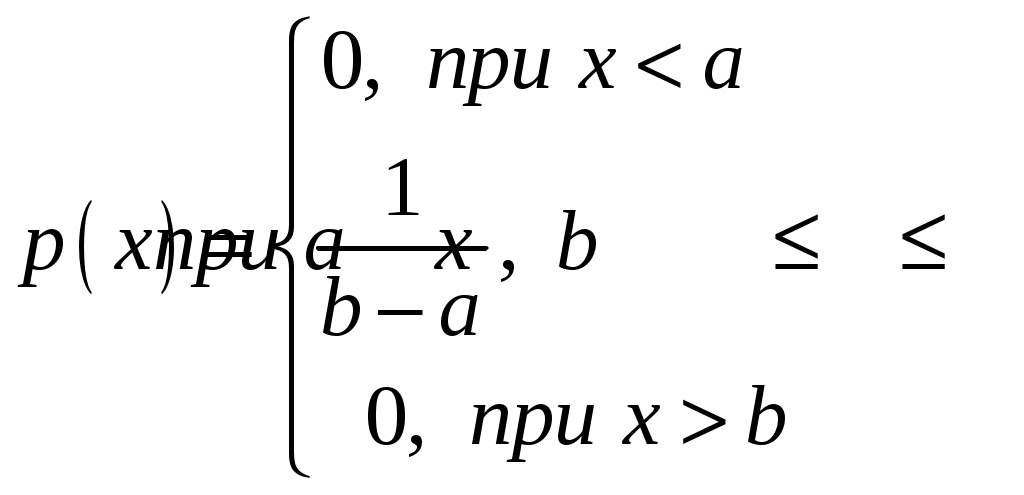 . .График дифференциальной функции равномерного закона НСВ X имеет вид: 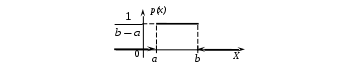 Интегральная функция распределения НСВ X, которая распределена по равномерному закону, имеет вид: 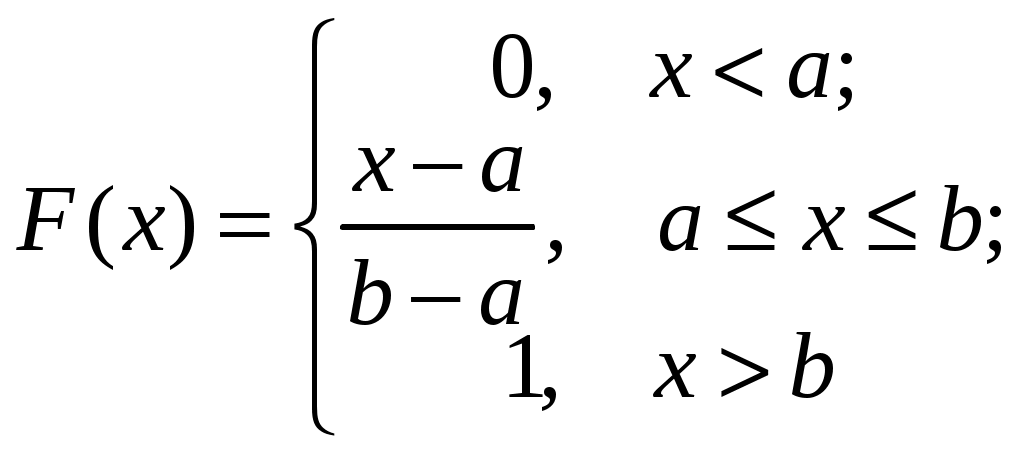 . .График интегральной функции равномерного закона НСВ X имеет вид:  Математическое ожидание и дисперсия равномерной СВ: 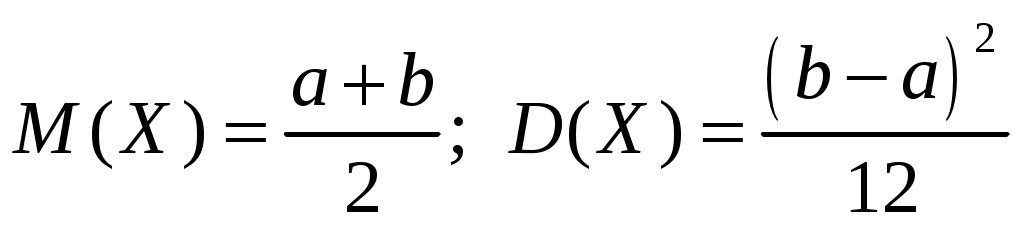 . .Применение: Надо отметить, что равномерный закон распределения применяется при работе с округленными числами, измерение каких-либо величин по шкале измерительного прибора. Пример 2.5. Цена деления шкалы измерительного прибора равна 0,2. Показания прибора округляются до ближайшего деления. Определить закон распределения ошибки округления. Найти среднеквадратическую ошибку округления . Найти вероятность того, что при отсчете будет сделана ошибка менее 0,04. Решение. Ошибку округления отсчета можно рассматривать как случайную величину 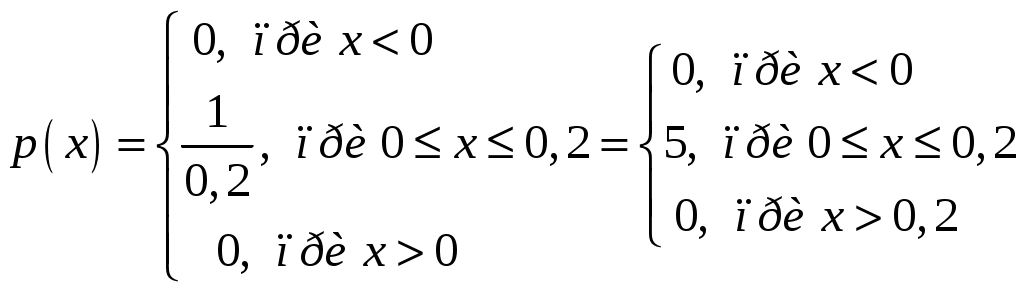 . .Сначала найдем дисперсию равномерной СВ 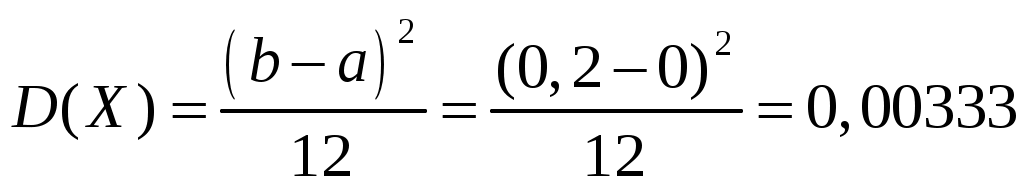 . .Используем формулу (2.11) и находим среднеквадратическую ошибку округления. Ошибка отсчета будет менее 0,04, если случайная величина заключена в интервале 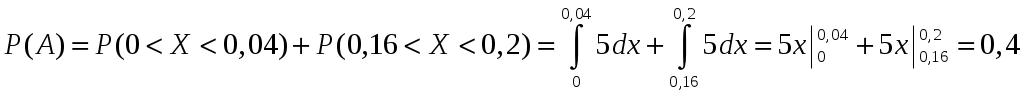 2.3.2. Показательное (экспоненциальное) распределение Непрерывная случайная величина X, которая принимает только неотрицательные значения с плотностью распределения, 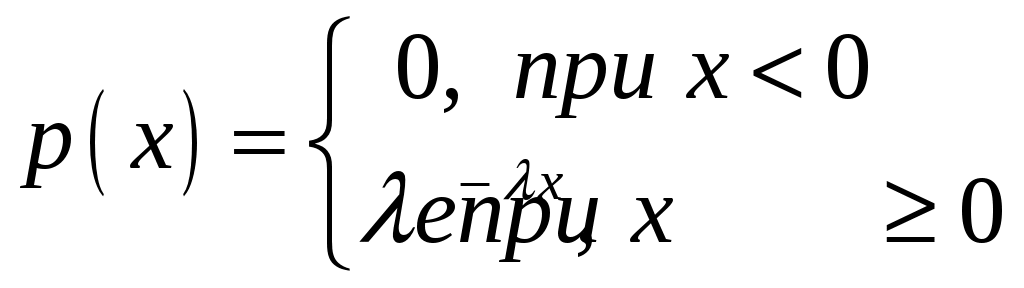 называется распределенной по показательному закону с параметром , где >0. График дифференциальной функции показательного закона НСВ X имеет вид: 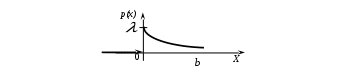 Интегральная функция распределения НСВ, распределенной по показательному закону, имеет вид: 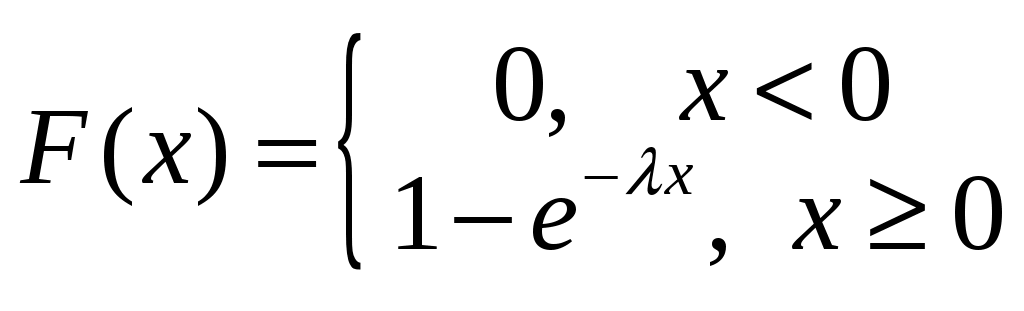 График интегральной функции показательного закона НСВ X имеет вид: 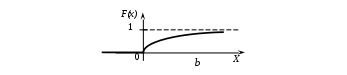 Математическое ожидание и дисперсия показательно распределенной СВ X: Применение: Надо отметить, что показательный закон распределения применяется в теории массового обслуживания; время ремонта, время простоя в очереди, время обслуживания. Пример 2.6. Технический осмотр и обслуживание машин продолжается в среднем 2 часа. Составить закон распределения, если СВ X время техосмотра машины, которое распределено по показательному закону. Найти среднее квадратическое отклонение. Найти вероятность того, что машина пройдет техосмотр менее чем за 1 час. Решение. Среднее время техосмотра равно 2 часа, а это математическое ожидание 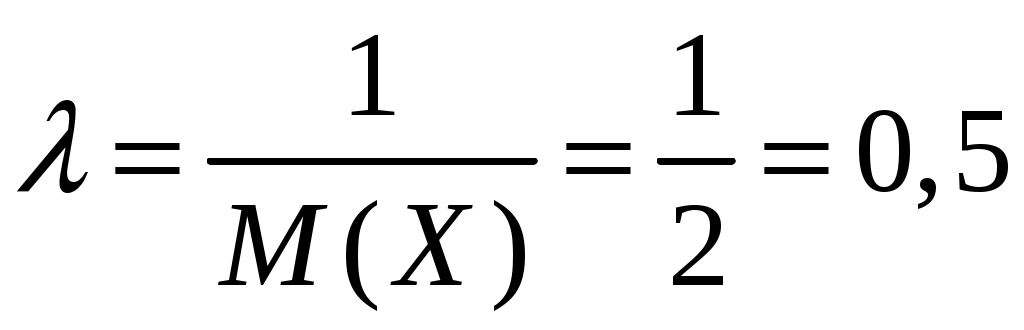 . Плотность распределения вероятностей СВ X имеет следующий вид: . Плотность распределения вероятностей СВ X имеет следующий вид: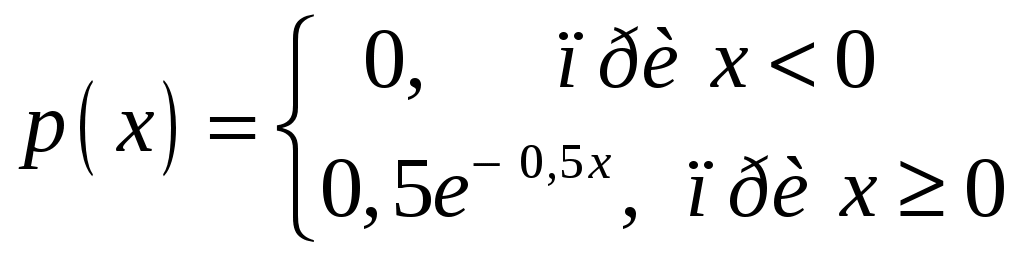 . .Интегральная функция распределения СВ X имеет следующий вид: 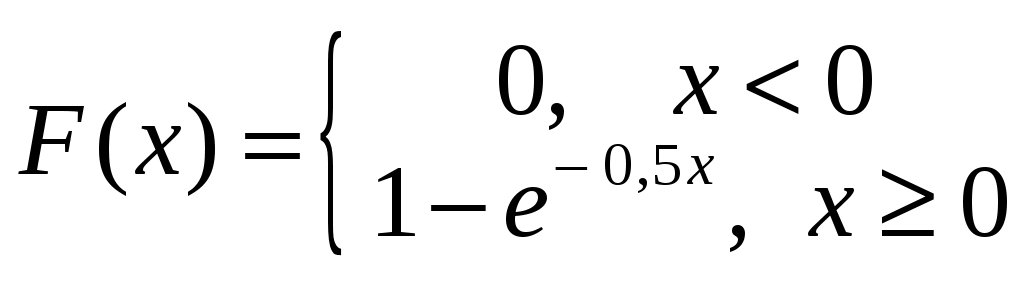 . .Для показательного закона распределения 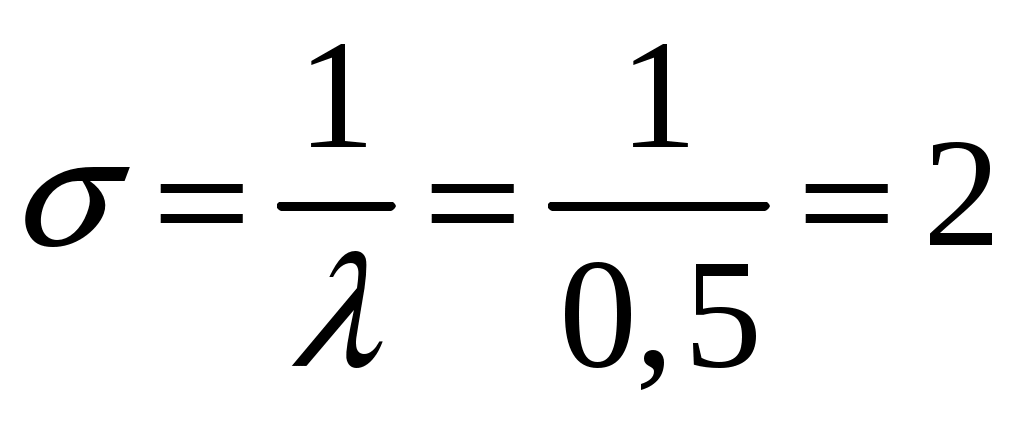 . .Чтобы найти вероятность того, что машина пройдет техосмотр менее чем на 1 час, воспользуемся формулой (2.1): 2.3.3. Элементы теории надежности Показательное распределение широко применяется в приложениях, в частности, в теории надежности, одним из основных понятий которой является функция надежности. 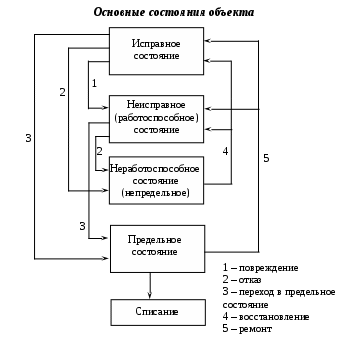 Термины и их определения в области надежности регламентирует ГОСТ 27.00289 «Надежность в технике», который содержит 85 терминов. Надежность – свойство объекта сохранять во времени в установленных пределах значения всех параметров, характеризующих способность выполнять требуемые функции в заданных режимах и условиях применения, технического обслуживания, ремонта, хранения и транспортирования. Объект (машина, станок, прибор, датчик и т.д.) может находиться в следующих состояниях (см. рисунок): исправном, неисправном (работоспособном), неработоспособном (непредельном), предельном. Работоспособное состояние – состояние объекта, при котором значения всех параметров, характеризующих способность выполнять заданные функции, соответствуют требованиям нормативно-технической и (или) конструкторской документации. Объект может находиться в работоспособном, но неисправном состоянии (например, из-за повреждения в виде вмятин или царапин на корпусе) Повреждение – некоторое событие, которое заключается в нарушении исправного состояния при сохранении работоспособного состояния. Переход объекта из работоспособного состояния в неработоспособное происходит в результате отказа. Отказы следует отличать от повреждений, при которых изделие становится не соответствующим хотя бы одному из требований технических условий, но сохраняет свою работоспособность. Отказ – событие, заключающееся в нарушении работоспособности объекта. Существует 8 видов отказов: внезапный, постепенный, независимый, зависимый, перемежающийся, конструкционный, производственный, эксплуатационный. По физическому смыслу, последствиям и специфике проявления особо значимыми являются внезапный и постепенный отказы. Дадим характеристику свойства безотказности. Безотказность – свойство объекта непрерывно сохранять работоспособное состояние до наступления предельного состояния при установленной системе технического обслуживания и ремонта в течение некоторого времени или наработки. Следует учитывать четыре важных специфических аспекта надежности: комплексный характер, т.е. связь надежности со всеми этапами жизненного цикла изделий (проектирование, изготовление, эксплуатация); фактор времени, так как оценивается изменение начальных параметров в процессе эксплуатации изделия. Рассматривать проблему надежности абстрактно (вне времени) не имеет смысла; прогнозирование поведения изделия с точки зрения сохранения его выходных параметров (показателей надежности); вероятностный характер отказов, процессов, параметров и показателей, определяемой некоторой случайной функцией (или событиями). Эта специфика отражена в показателях надежности. Основной показатель надежности изделия – вероятность безотказной работы Допустимые значения в авиации в машиностроении у станков с ЧПУ, оснащенных системами диагностики В электронной промышленности надежность датчика должна рассматриваться в двух аспектах: 1) механическая надежность – механическая прочность конструкции датчика, целостность его конфигурации, целостность его электрических цепей, безусловная герметичность узла уплотнения в условиях эксплуатации датчика; 2) метрологическая надежность Метрологическая надежность является одной из важнейших характеристик датчиков. Можно условно установить следующие уровни метрологической надежности: Будем называть элементом некоторое устройство, независимо от того «простое» оно, или «сложное». Пусть элемент начинает работать в момент времени Таким образом, интегральная функция определяет вероятность отказа за время длительностью Вероятность отказа Следовательно, вероятность безотказной работы за это же время, длительностью Определение 2.9. Функцией надежности Часто длительность времени безотказной работы элемента имеет показательное распределение. Тогда для определения вероятности отказа используется интегральная функция, которая имеет вид: Следовательно, функция надежности, в случае показательного распределения времени безотказной работы элемента, имеет вид |
