математика. РАЗДЕЛ 2 Случайные величины doc. Определение Величина, которая в зависимости от случая может принимать те или другие числовые значения, называется случайной
 Скачать 1.49 Mb.
|
|
Определение 1.7. Дисперсией (рассеянием) дискретной СВ называют математическое ожидание квадрата отклонения СВ от ее математического ожидания:  . (1.3)Для вычисления дисперсии часто бывает удобно пользоваться следующей теоремой. Теорема 1.1. Дисперсия равна разности между математическим ожиданием квадрата СВ X и квадратом ее математического ожидания:  . (1.4)Свойства дисперсии Свойство 1. Дисперсия постоянной величины  равна нулю: .Свойство становится ясным, если учесть, что постоянная величина сохраняет одно и то же значение и рассеяние, конечно, не имеет. Свойство 2. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат:  .Свойство 3. Дисперсия суммы двух независимых СВ равна сумме дисперсий этих величин:  .Свойство 4. Дисперсия разности двух независимых СВ равна сумме дисперсий этих величин:  .Свойства примем без доказательства. Дисперсия как мера рассеивания значений СВ обладает тем недостатком, что ее размерность не совпадает с размерностью СВ (размерность дисперсии – это квадрат размерности СВ). Поэтому вводится еще одна мера рассеивания с размерностью, совпадающей с размерностью СВ. Это так называемое среднее квадратическое отклонение. Определение 1.8. Средним квадратическим отклонением СВ X называют квадратный корень из дисперсии:  . (1.5)Дадим определение еще одной числовой характеристики, как мода ДСВ. Определение 1.9. Модой MoДСВXназывается ее наиболее вероятное значение. Пример 1.3. СВ X задана законом распределения: 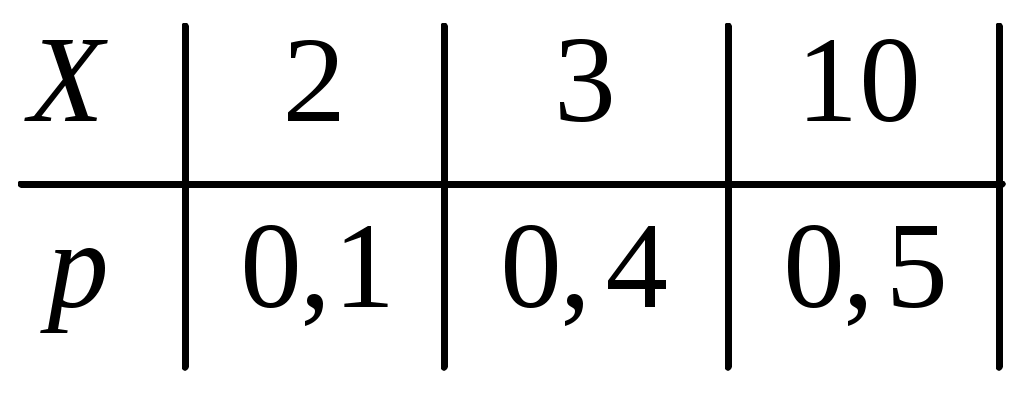 .Построить функцию распределения и ее график. Найти числовые характеристики заданного закона распределения. Решение. 1) Найдем функцию распределения ДСВ X. Значения СВ X:  разбивают числовую прямую на четыре промежутка  .Если  , то  .Если  , то  .Если  , то  .Если  , то  .Таким образом, получаем следующую функцию распределения: 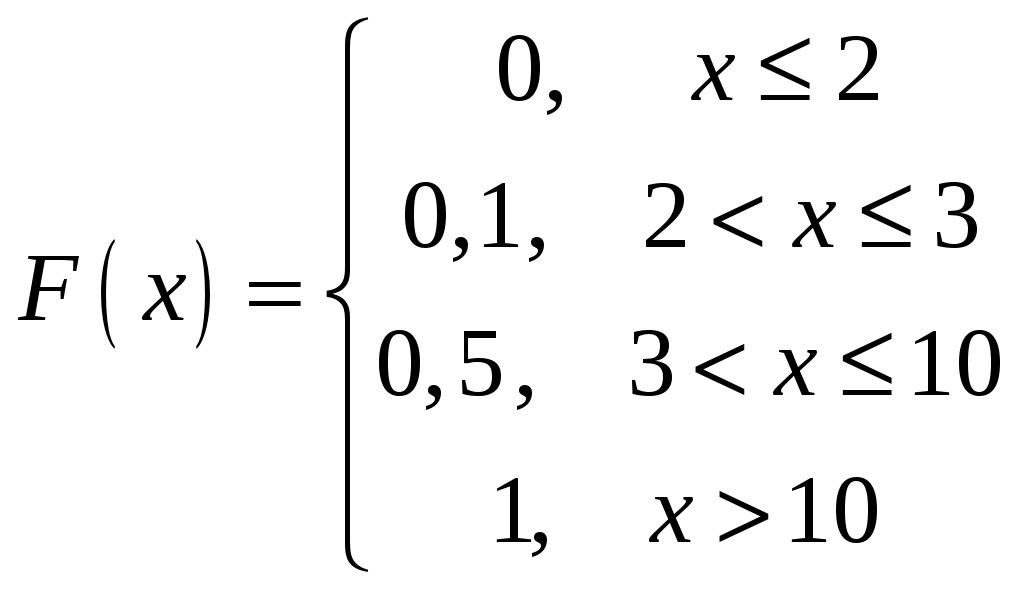 .График данной функции имеет вид: 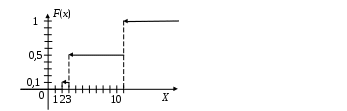 2) Найдем числовые характеристики ДСВ X. Найдем математическое ожидание:  .Найдем дисперсию:  .Найдем среднее квадратическое отклонение:  .Мода соответственно равна Mo=10. Пример 1.4. Найти закон распределения ДСВ  , которая может принимать только два значения  с вероятностью  и  (причем  ), если известны математическое ожидание  и дисперсия  .Решение. Поскольку 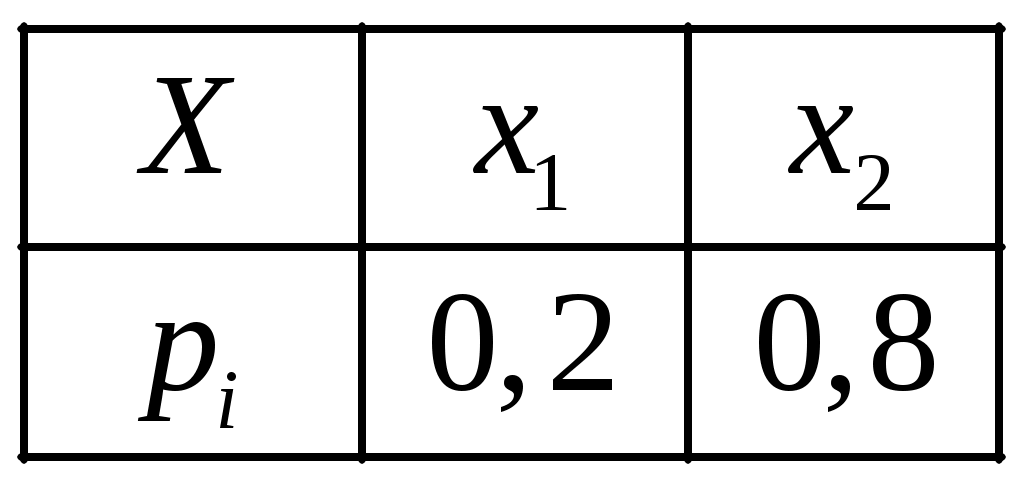, а  , то  . Тогда имеем следующий закон распределения: .По формулам (1.2) и (1.4) получаем:  ; .Составляем систему уравнений 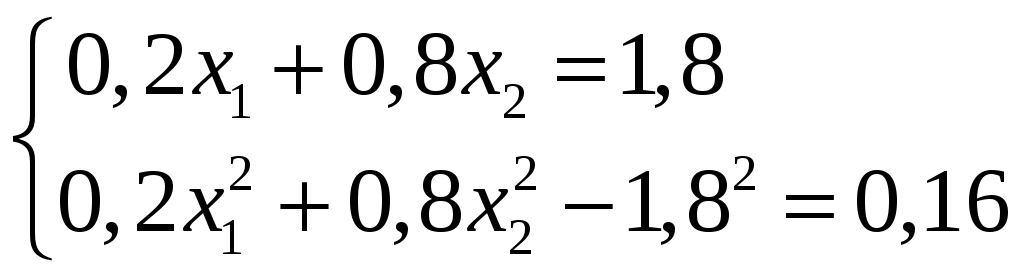 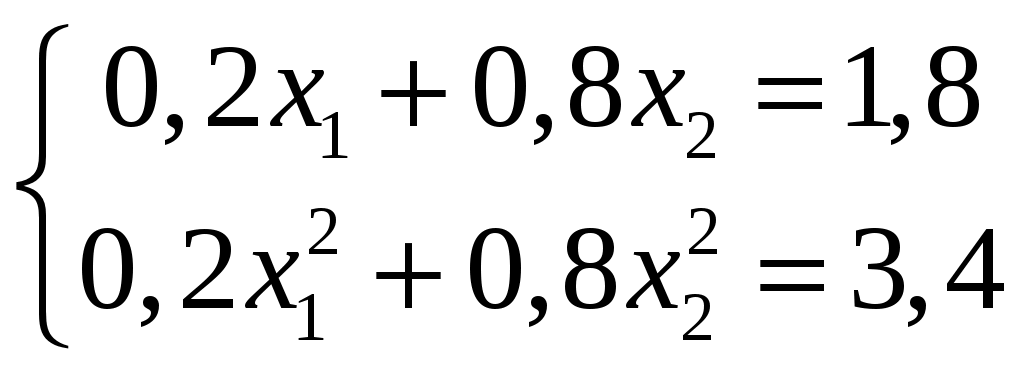 .Решив систему уравнений, получаем два решения:  ,  или  ,  . По условию задачи подходит первое решение.Итак, , . 1.3. Законы распределения ДСВ Рассмотрим некоторые законы распределения дискретной СВ. Биномиальное распределение Пусть имеется  испытаний Бернулли с вероятностью успеха  и неуспеха  ,  . Дискретная СВ X – число успехов имеет распределение Это распределение называется биномиальным с параметрами p и q. Математическое ожидание и дисперсия СВ X:  ,  .Геометрическое распределение Дискретная СВ X имеет геометрическое распределение, если она принимает значения  (счетное множество значений) с вероятностью где  ,  Случайная величина , имеющая геометрическое распределение, представляет собой число Бернулли до первого успеха.Математическое ожидание и дисперсия 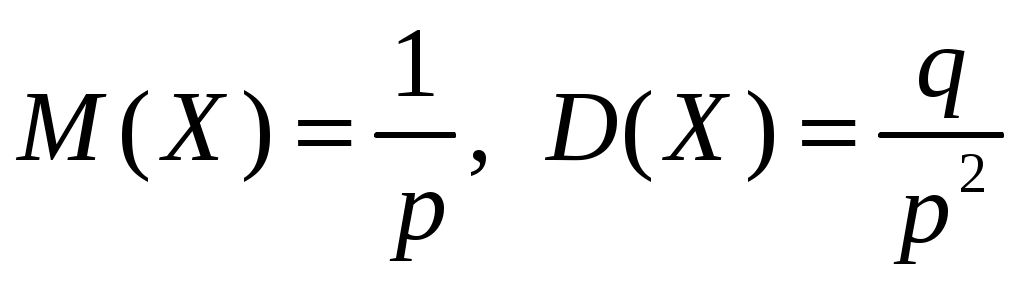: .Гипергеометрическое распределение Дискретная СВ X имеет гипергеометрическое распределение, если она принимает значения 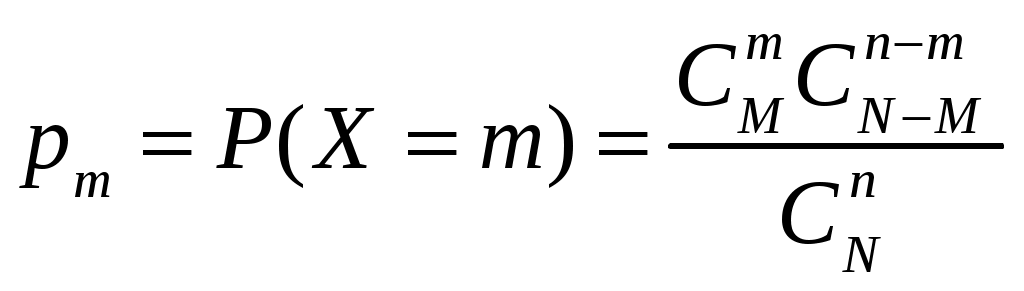 с вероятностями где  ;  . Вероятность  является вероятностью выбора объектов, обладающих заданным свойством, из множества n объектов, случайно извлеченных (без возврата) из совокупности  объектов, среди которых  объектов обладают заданным свойством.Математическое ожидание и дисперсия СВ, имеющей гипергеометрическое распределение с параметрами 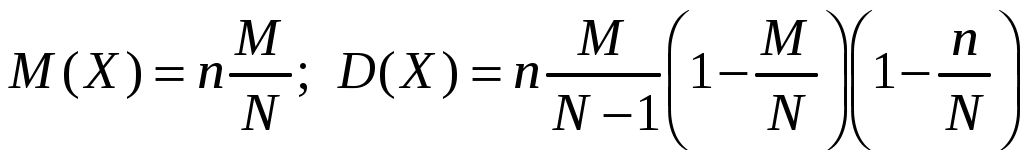, , : .Закон Пуассона Говорят, что СВ X распределена по закону Пуассона, если она принимает целые значения 0, 1, 2, … с вероятностями 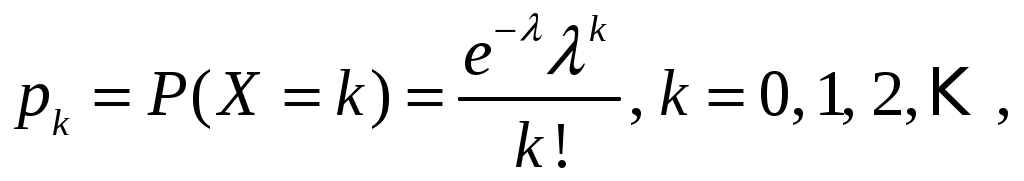 где  – параметр распределения,  ,  - число появления события  в независимых испытаниях.Математическое ожидание и дисперсия пуассоновской СВ равны параметру распределения:  .Закону распределения Пуассона обычно подчинена СВ, задающая простейший поток событий (число вызовов скорой помощи, число вызовов на АТС, число заказов на предприятии бытовых услуг, и т.д.) Если интенсивность потока 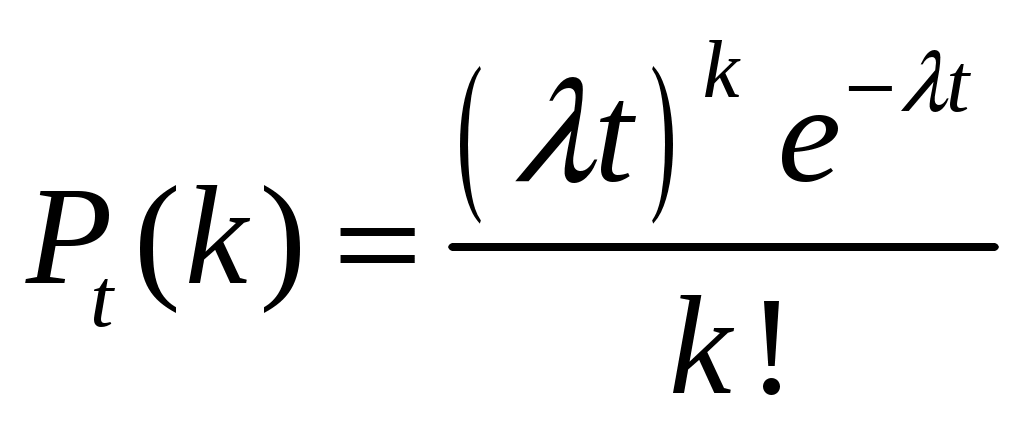 выражает число появлений события за единицу времени, то вероятность наступления событий за время  определяется формулой Пуассона  .Пример 1.5. Из 25 подписчиков на газеты 16 человек подписались на местные газеты, остальные – на республиканские. Наудачу выбрали 3 подписчиков. СВ X – количество подписчиков на местные газеты среди выбранных. Записать закон распределения СВ X. Составить функцию распределения и построить ее график. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение. Найти  .Решение. 1) Среди трех отобранных подписчиков количество человек, подписавшиеся на местные газеты может принимать следующие значения: 0, 1, 2, 3. Значит, СВ X имеет значения 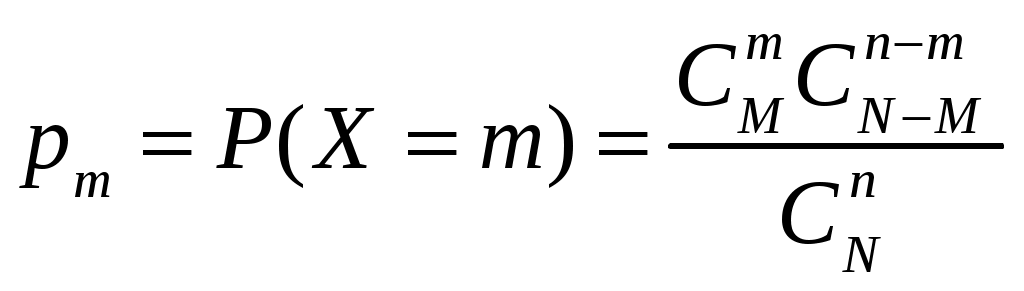 . 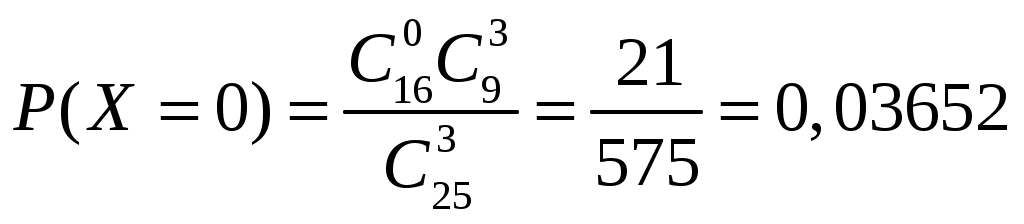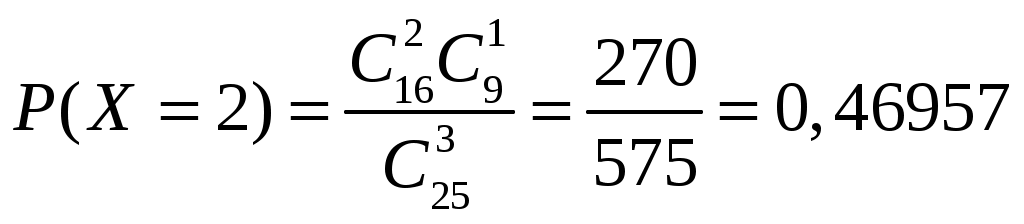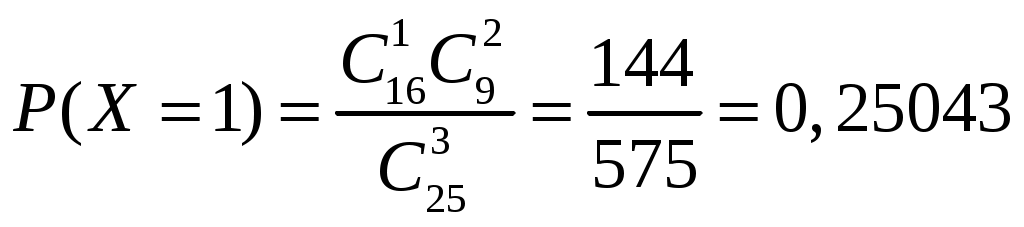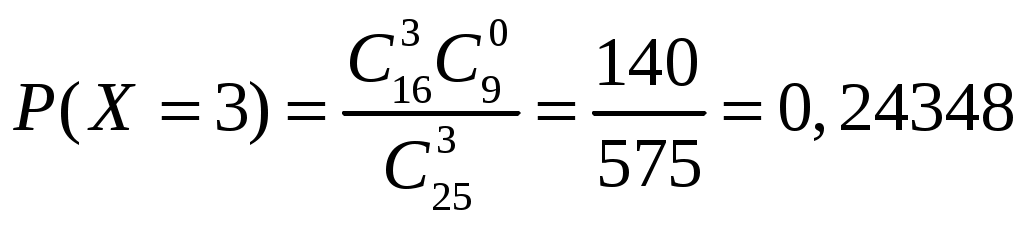Данная СВ X распределена по гипергеометрическому закону. Поэтому вероятности появления каждой СВ X находим по формуле: . ;  ; ;  .Для контроля  +0,46957+0,24348=1. Записываем закон распределения ДСВ X в виде таблицы:
2) Данные значения СВ X разбивают числовую прямую на пять промежутков. Если  , то ;Если  , то  ;Если  , то  ;Если  , то  +0,46957=0,75652; Если  , то  +0,25043+0,46957+0,24348=1. Таким образом, получаем следующую функцию распределения 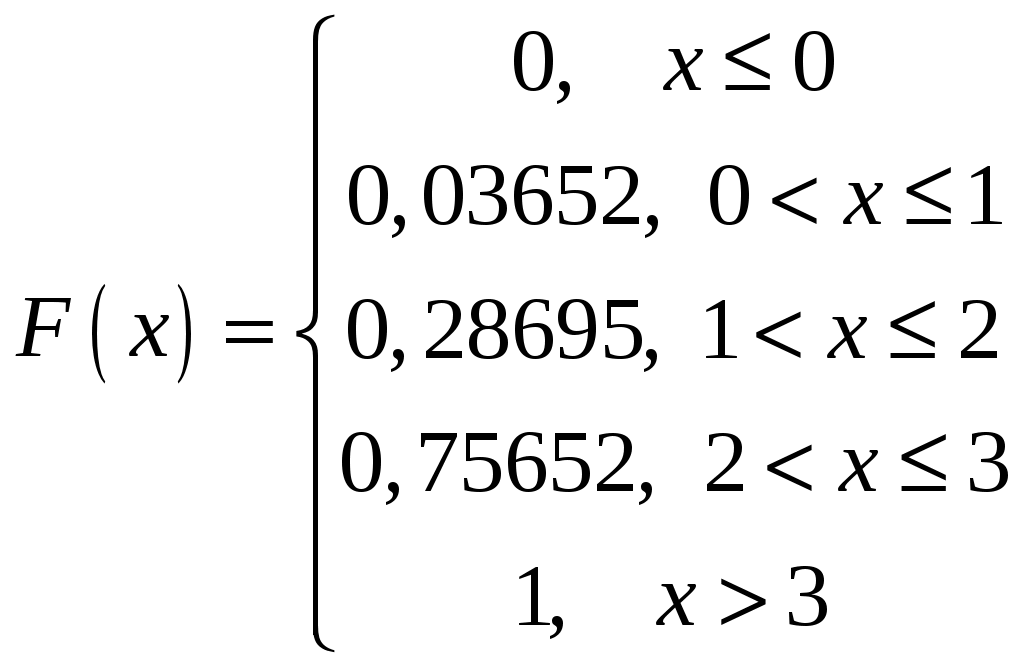 .Строим график функции распределения: 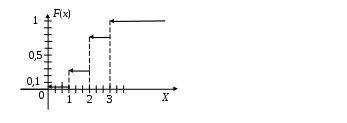 3) Находим математическое ожидание СВ X:  .Найдем дисперсию:  =0,63363≈0,634 Найдем среднее квадратическое отклонение:  . ; . 2. НЕПРЕРЫВНЫЕ ОДНОМЕРНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ |