математика. РАЗДЕЛ 2 Случайные величины doc. Определение Величина, которая в зависимости от случая может принимать те или другие числовые значения, называется случайной
 Скачать 1.49 Mb. Скачать 1.49 Mb.
|
|
Пример 2.10. Случайная величина Xраспределена по нормальному закону. Математическое ожидание и дисперсия этой величины соответственно равны 20 и 100. Найти вероятность того, что отклонение по абсолютной величине будет меньше трех. Решение. По условию Значение функции (0,3) находим по таблице значений интегральной функции Лапласа. Далее мы рассмотрим так называемое правило «трех сигм». Преобразуем формулу 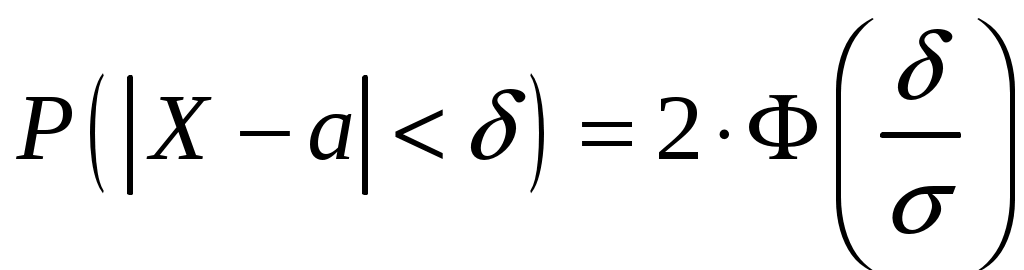 , ,положив 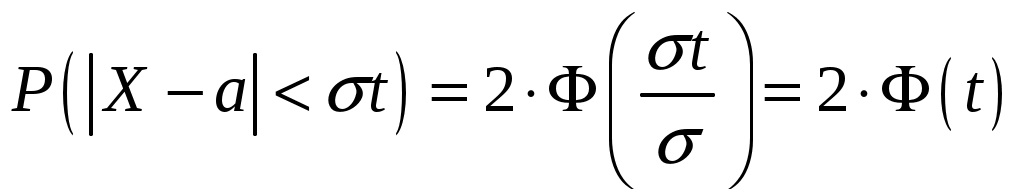 . .Если т.е. вероятность того, что отклонение по абсолютной величине будет меньше утроенного среднего квадратического отклонения, равна 0,9973. Другими словами, вероятность того, что абсолютная величина отклонения превысит утроенное среднее квадратическое отклонение, очень мала, а именно равна 0,0027. Это означает, что лишь в 0,27 % случаев так может произойти. Такие события, исходя из принципа невозможности маловероятных событий, можно считать практически невозможными. В этом и состоит сущность правила трех сигм: если случайная величина распределена нормально, то абсолютная величина ее отклонения от математического ожидания не превосходит утроенного среднего квадратического отклонения. На практике правило трех сигм применяется так: если распределение изучаемой случайной величины неизвестно, но условие, указанное в приведенном правиле, выполняется, то имеются основания предполагать, что изучаемая величина распределена нормально; в противном случае она не распределена нормально. 3. МОМЕНТЫ СЛУЧАЙНОЙ ВЕЛИЧИНЫ Выше были рассмотрены числовые характеристики СВ: математическое ожидание, дисперсия и среднее квадратическое отклонение. Рассмотрим ДСВ X, заданную законом распределения: 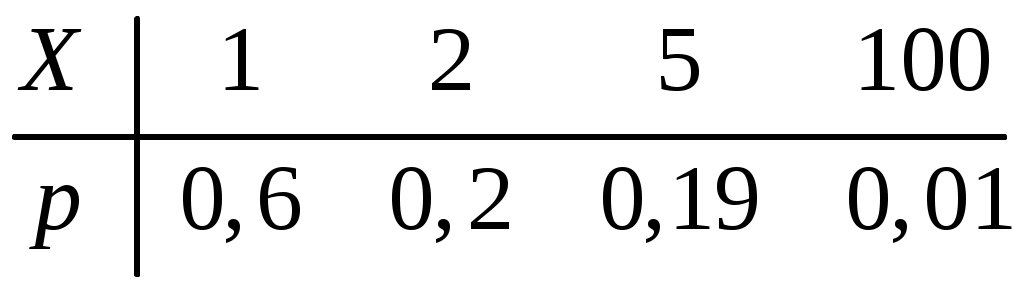 Найдем математическое ожидание X: Напишем закон распределения X2: 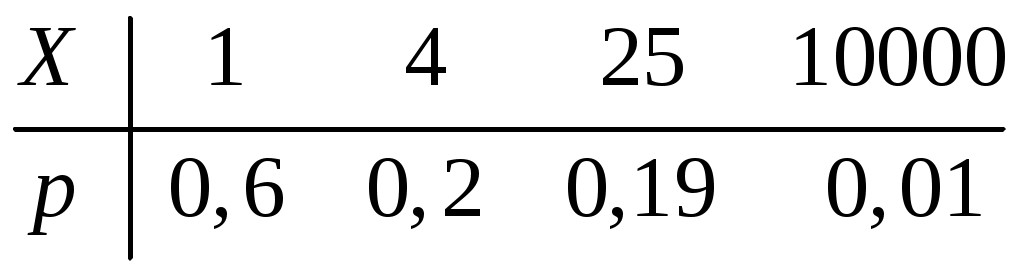 . .Найдем математическое ожидание X2: Мы видим, что Таким образом, переход от Определение 3.1. Начальным моментом k-го порядка СВ X называют математическое ожидание величины Для ДСВ X и НСВ X начальные моменты можно находить по следующим формулам: 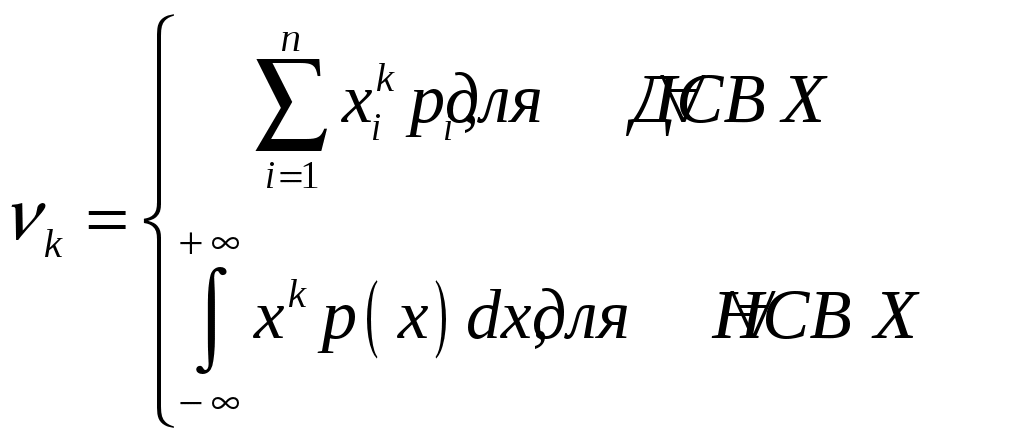 . (3.2) . (3.2)В частности, Кроме моментов СВ X, целесообразно рассматривать моменты отклонения Определение 3.2. Центральным моментом k-го порядка СВ X называют математическое ожидание величины Для ДСВ X и НСВ X центральные моменты можно находить по следующим формулам: 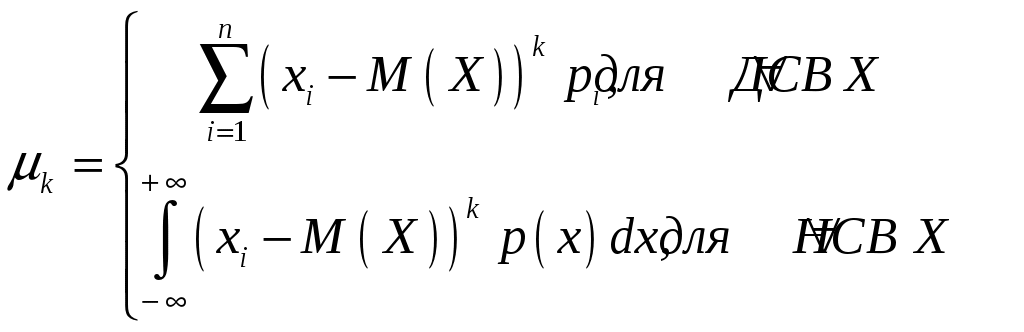 . (3.4) . (3.4)В частности, Моменты более высоких порядков применяются редко. Пример 3.1. Дискретная случайная величина X задана законом распределения: 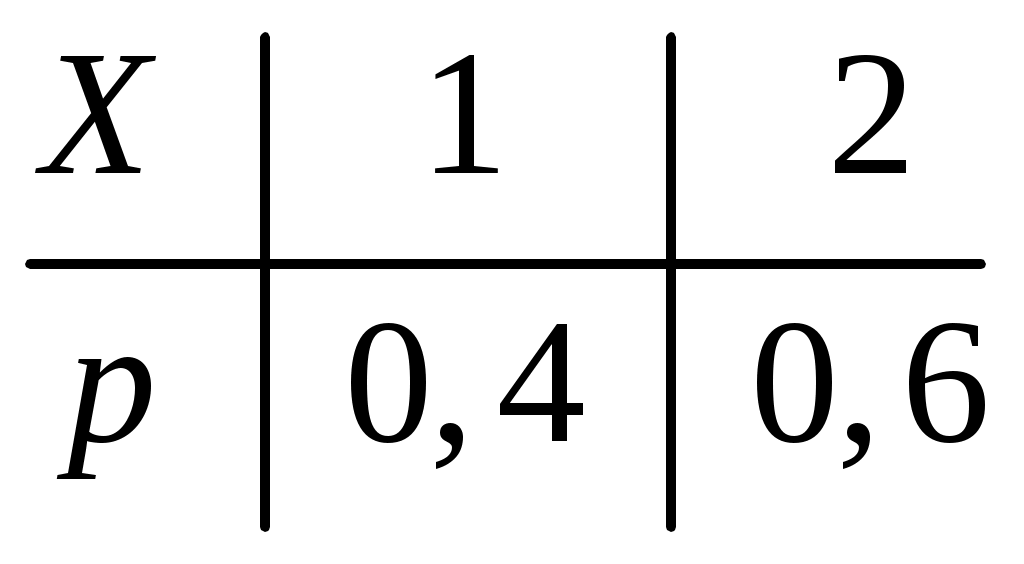 . .Найти начальные и центральные моменты первого, второго и третьего порядков СВX. Решение. В соответствии с формулой (3.2) находим сначала начальные моменты: Вычислим центральные моменты, согласно формуле (3.4): Эмпирическим распределением называют распределение относительных частот. Такие распределения изучает математическая статистика. Теоретическим распределением называют распределение вероятностей. Такие распределения изучает теория вероятностей. При изучении распределений, отличных от нормального, возникает необходимость количественно оценить это различие. С этой целью вводят специальные характеристики, в частности, ассиметрию и эксцесс. Для нормального распределения эти характеристики равны нулю. Поэтому, если ассиметрия и эксцесс изучаемого распределения имеют небольшие значения, отличные от нуля, то можно предположить близость этого распределения к нормальному. Большие же значения ассиметрии и эксцесса указывают на значительное отклонение от нормального. Можно доказать, что для симметричного распределения плотности вероятностей (график такого распределения симметричен относительно прямой Определение 3.3. Ассиметрией теоретического распределения называют отношение центрального момента третьего порядка к кубу среднего квадратического отклонения: 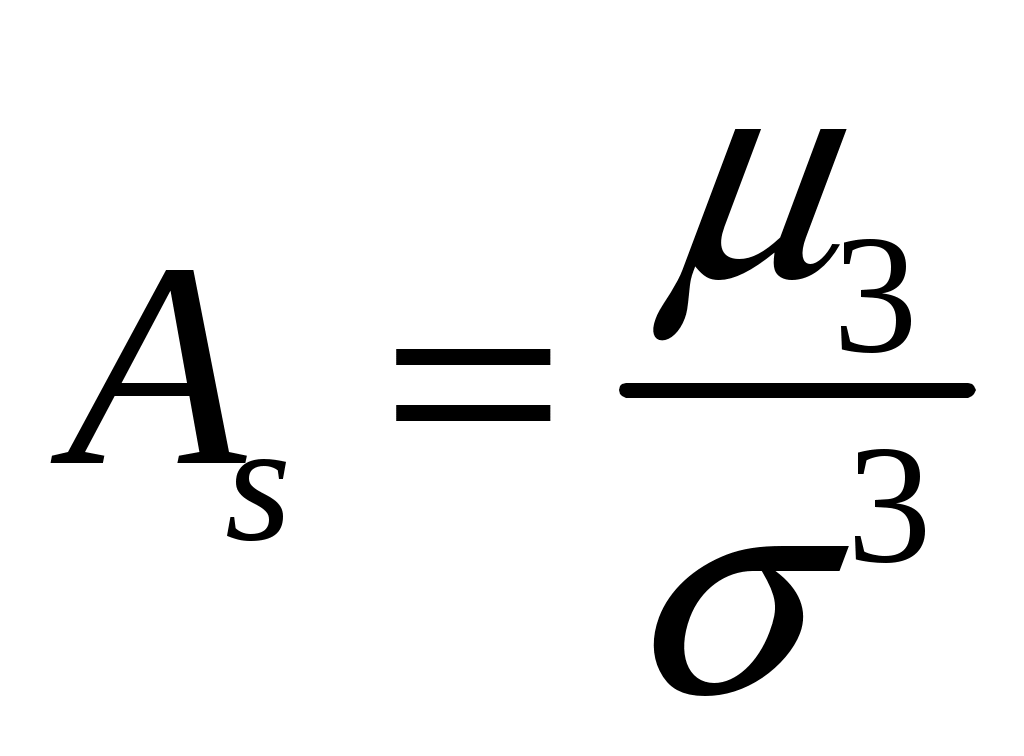 . (3.5) . (3.5)Ассиметрия положительна, если «длинная часть» кривой распределения расположена справа от математического ожидания; ассиметрия отрицательна, если «длинная часть» кривой расположена слева от математического ожидания. Практически определяют знак ассиметрии по расположению кривой относительно моды. Для оценки «крутости», т.е. большего или меньшего подъема кривой теоретического распределения по сравнению с нормальной кривой, пользуются характеристикой - эксцессом. Четвертый центральный момент служит для характеристики крутости распределения X по сравнению с крутостью распределения нормальной СВ. Определение 3.4. Эксцессом теоретического распределения называют характеристику, которая определяется равенством Для нормального распределения Если эксцесс некоторого распределения отличается от нуля, то кривая этого распределения отличается от нормальной кривой: если эксцесс положительный, то кривая имеет более высокую и «острую» вершину, чем нормальная кривая; если эксцесс отрицательный, то сравниваемая кривая имеет более низкую и «плоскую» вершину, чем нормальная кривая. 4. ЗАКОН БОЛЬШИХ ЧИСЕЛ Нельзя заранее уверенно предвидеть, какое из возможных значений примет случайная величина в итоге испытания; это зависит от многих причин, учесть которые мы не в состоянии. Казалось бы, что о каждой случайной величине мы располагаем в этом смысле весьма скромные сведения, то вряд ли можно установить закономерности поведения и суммы достаточно большого числа случайных величин. На самом деле это не так. Оказывается, что при некоторых сравнительно широких условиях суммарное поведение достаточно большого числа случайных величин почти утрачивает случайный характер и становится закономерным. Для практики очень важно знание условий, при выполнении которых совокупное действие очень многих случайных причин приводит к результату, почти не зависящему от случая, так как позволяет предвидеть ход явлений. Эти условия и указываются в теоремах, носящих общее название закона больших чисел. К ним относятся теоремы Чебышева и Бернулли. Теорема Чебышева является наиболее общим законом больших чисел, теорема Бернулли – простейшей. Прежде, чем перейти к рассмотрению этих теорем, мы введем сначала неравенство Маркова и неравенство Чебышева, которые примем без доказательства. Теорема 4.1 (неравенство Маркова). Если случайная величина X может принимать только неотрицательные значения и у нее есть математическое ожидание, то каково бы не было положительное число 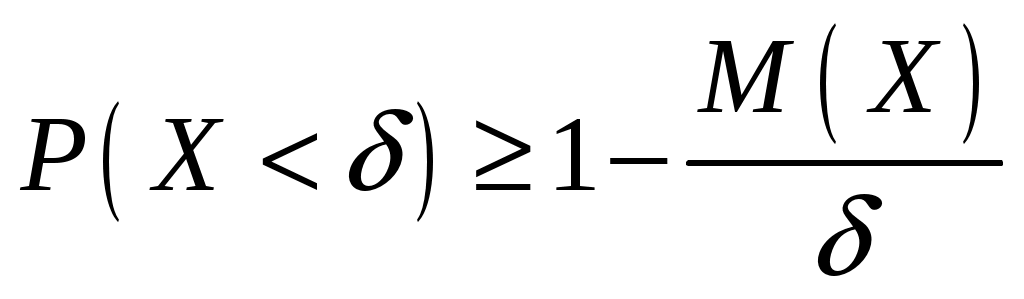 . (4.1) . (4.1)В этом случае выполняется и неравенство 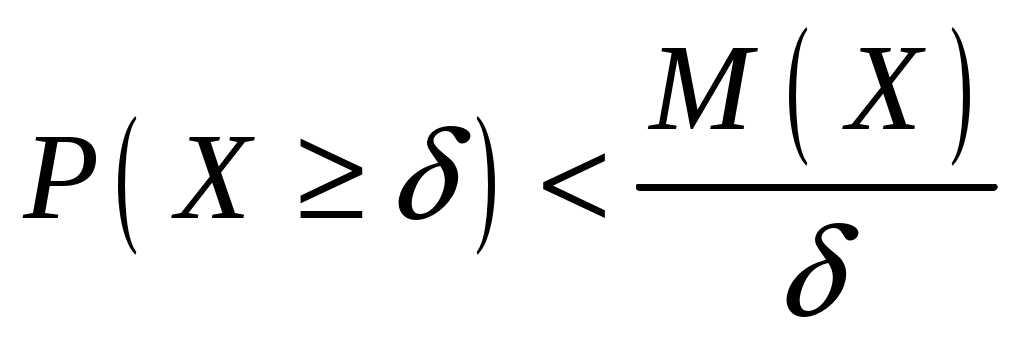 . (4.2) . (4.2)Теорема 4.2 (неравенство Чебышева). Каково бы ни было 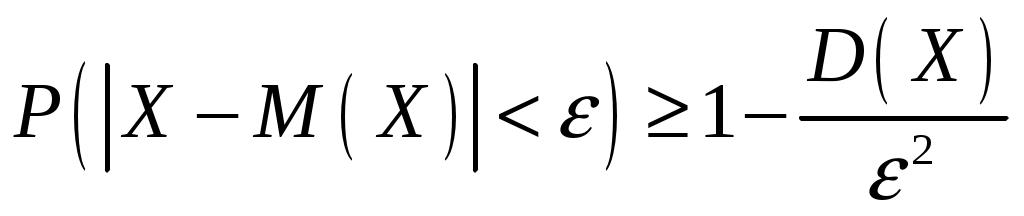 . (4.3) . (4.3)В этом случае выполняется и неравенство Пример 4.1. Средний срок службы мотора 4 года. Оценить вероятность того, что данный мотор не прослужит более 20 лет. Решение. Пусть случайная величина X – срок службы мотора. Из условия задачи следует, что Пример 4.2. Электростанция обслуживает сеть из 18000 ламп, вероятность включения каждой из которых в зимний вечер равна 0,9. Оценить вероятность того, что число ламп, включенных в сеть зимним вечером, отличается от своего математического ожидания по абсолютной величине менее чем на 200. Решение. Пусть случайная величина X – число включенных рамп. Случайная величина распределена по биноминальному закону с математическим ожиданием Точное значение можно было бы определить, используя формулу 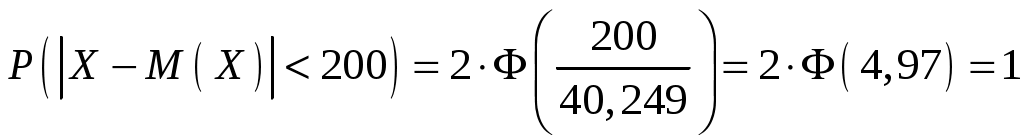 . . Замечание: Неравенство Чебышева имеет для практики ограниченное значение, поскольку часто дает грубую, а иногда и тривиальную (не представляющую интереса) оценку. Теоретическое же значение неравенства Чебышева весьма велико, поскольку с помощью этого неравенства доказывается теорема Чебышева. Теорема 4.3 (теорема Чебышева). Если 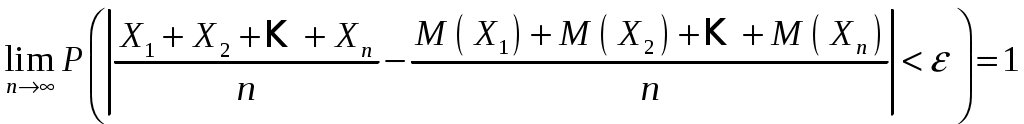 . (4.5) . (4.5)Следствие. Если 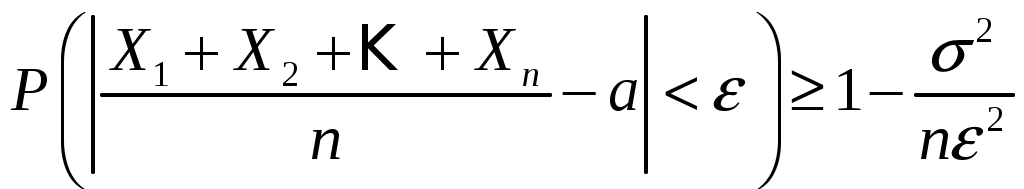 , (4.6) , (4.6)и 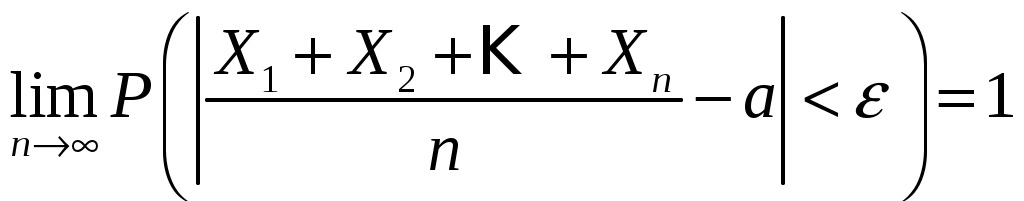 . (4.7) . (4.7)Отсюда видно, что среднее арифметическое значение величин Сущность доказанной теоремы Чебышева и следствия из этой теоремы такова: хотя отдельные независимые случайные величины могут принимать значения далекие от своих математических ожиданий, среднее арифметическое достаточно большого числа случайных величин с большой вероятностью принимает значения, близкие к определенному постоянному числу, а именно к числу Итак, среднее арифметическое достаточно большого числа независимых случайных величин (дисперсия которых равномерно ограничены) утрачивает характер случайной величины. Объясняется это тем, что отклонение каждой из величин от своих математических ожиданий могут быть как положительными, так и отрицательными, а в среднем арифметическом они взаимно погашаются. Теорема Чебышева справедлива не только для дискретных, но и для непрерывных случайных величин. Доказанная теорема Чебышева и следствие из нее имеют большое практическое применение. Обычно для измерения некоторой физической величины производят несколько измерений и их среднее арифметическое принимают в качестве искомого размера. При каких условиях этот способ измерения можно считать правильным? Ответ на этот вопрос дает теорема Чебышева (ее частный случай). Действительно, рассмотрим результаты каждого измерения как случайные величины Первое требование выполняется, если результат каждого измерения не зависит от результатов остальных. Второе требование выполняется, если измерения произведены без систематических (одного знака) ошибок. В этом случае математическое ожидание всех случайных величин одинаковы и равны истинному размеру a. Третье требование выполняется, если прибор обеспечивает определенную точность измерений. Хотя при этом результаты отдельных измерений различны, но рассеяние их ограниченно. Если все указанные требования выполнены, то вправе применить к результатам измерений теорему Чебышева или следствие из нее. Среднее арифметическое значение результатов измерений с ростом Однако ошибочно думать, что, увеличивая число измерений можно достичь сколь угодно большой точности. Дело в том, что сам прибор дает показания лишь с точностью На теореме Чебышева основан широко применимый в статистике выборочный метод, суть которого состоит в том, что по сравнительно небольшой случайной выборке судят обо всей совокупности (генеральной совокупности) исследуемых объектов. |
