математика. РАЗДЕЛ 2 Случайные величины doc. Определение Величина, которая в зависимости от случая может принимать те или другие числовые значения, называется случайной
 Скачать 1.49 Mb. Скачать 1.49 Mb.
|
|
Определение 2.10. Показательным законом надежности называют функцию надежности, определяемую равенством где интенсивность отказа. Эта формула позволяет найти вероятность безотказной работы элемента на интервале времени, длительностью Пример 2.7. Время безотказной работы элемента распределено по показательному закону с плотностью распределения Решение. По условию постоянная интенсивность отказа =0,02. Используя формулу, получаем вероятность того, что элемент проработает безотказно 100 часов. Показательный закон надежности весьма прост и удобен для решения задач, возникающих на практике. Очень многие формулы теории надежности значительно упрощаются. Объясняется это тем, что этот закон обладает следующим важным свойством: вероятность безотказной работы элемента на интервале длительностью Пример 2.8. Длительность времени безотказной работы каждого из трех элементов, входящих в техническое устройство, имеет показательное распределение. Среднее время безотказной работы для каждого элемента равно 500 ч. Техническое устройство работает при условии безотказной работы всех трех элементов. Определить вероятность безотказной работы устройства в течение не менее 800 ч, если время безотказной работы каждого элемента не зависит от времени работы двух других элементов. Решение. Искомая вероятность равна вероятности того, что в течение не менее 800 ч будут безотказно работать все три элемента устройства. Пусть событие Найдем теперь вероятность события Тогда вероятность события Таким образом, 2.3.4. Нормальное распределение Непрерывная случайная величина X имеет нормальное распределение (закон Гаусса) с параметрами a и , если её плотность вероятности имеет вид: 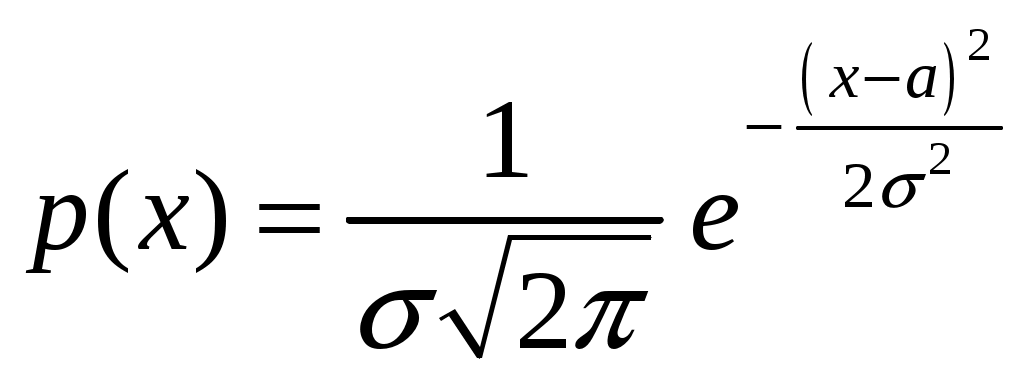 , где >0. , где >0.График дифференциальной функции нормального закона НСВ X имеет вид: 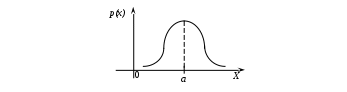 Обозначим через 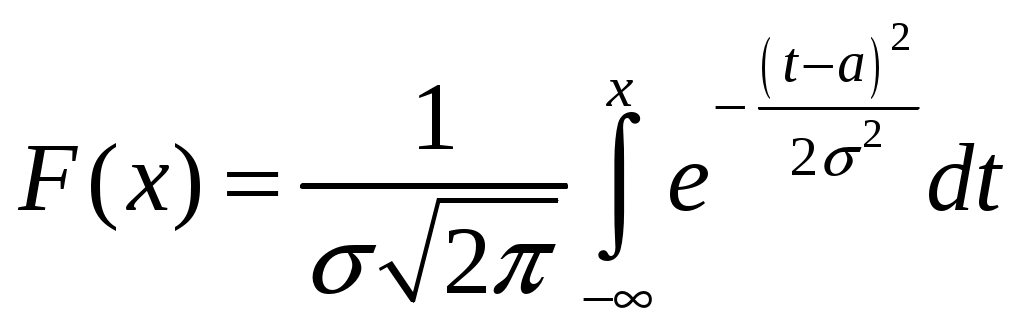 . .График интегральной функции нормального закона НСВ X имеет вид: 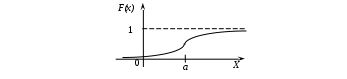 Мы видим, что нормальное распределение определяется двумя параметрами: a и . Достаточно задать эти параметры, чтобы задать нормальное распределение. Выясним вероятностный смысл этих параметров. 1) По определению математического ожидания непрерывной случайной величины 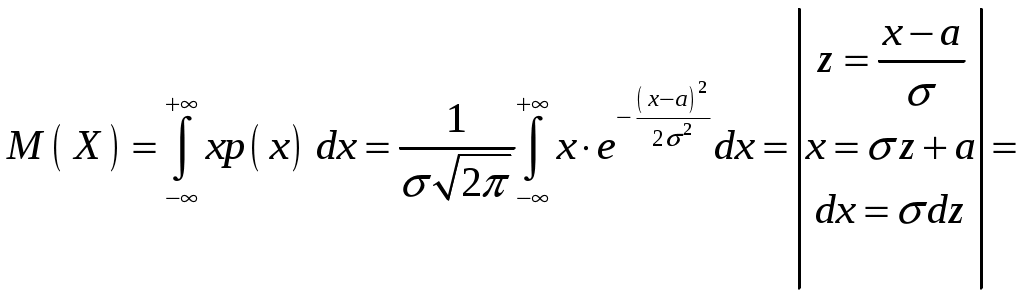 =(Приняв по внимание, что новые пределы интегрирования равны старым)= 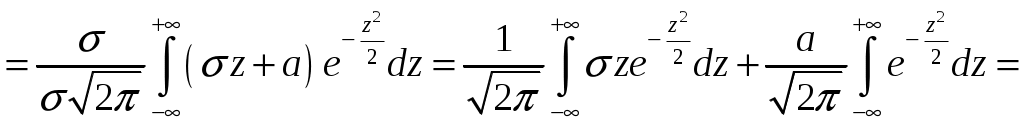 =(Первый интеграл: под знаком интеграла нечетная функция; пределы интегрирования симметричны относительно начала координат. Второй интеграл: интеграл Пуассона 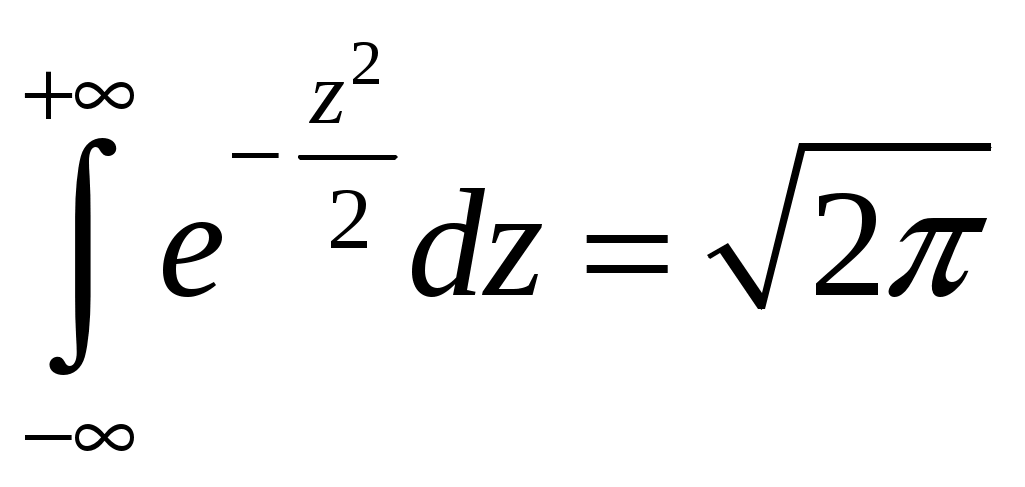 .) .)Итак, 2) По аналогии можно показать, что дисперсия непрерывной случайной величины, которая распределена по нормальному закону распределения, равна Следовательно, Итак, среднее квадратическое отклонение нормального распределения равно параметру . Применение: Надо отметить, что по нормальному закону распределено большое количество случайных величин. Этому закону подчиняется распределение роста двадцатилетнего мужчины; вес женщины, рост которой равен 170 см; дальность полета снаряда; результат измерения длины, массы, времени и т.д. Нормированным (стандартным) называют нормальное распределение с параметрами a=0 и =1. Например, если X – нормальная величина с параметрами a и , то Дифференциальная функция нормированного распределения 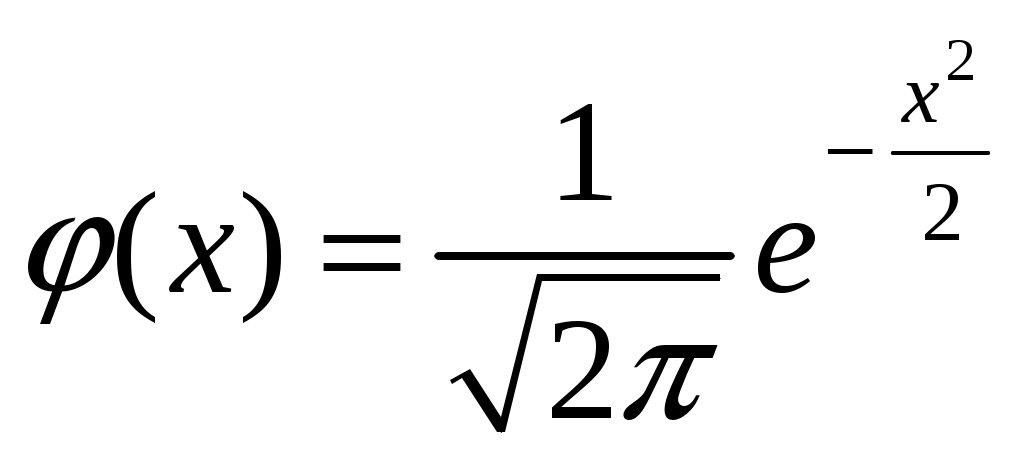 . .Эта функция табулирована (таблица локальной функции Лапласа). Интегральная функция нормированного распределения имеет вид: 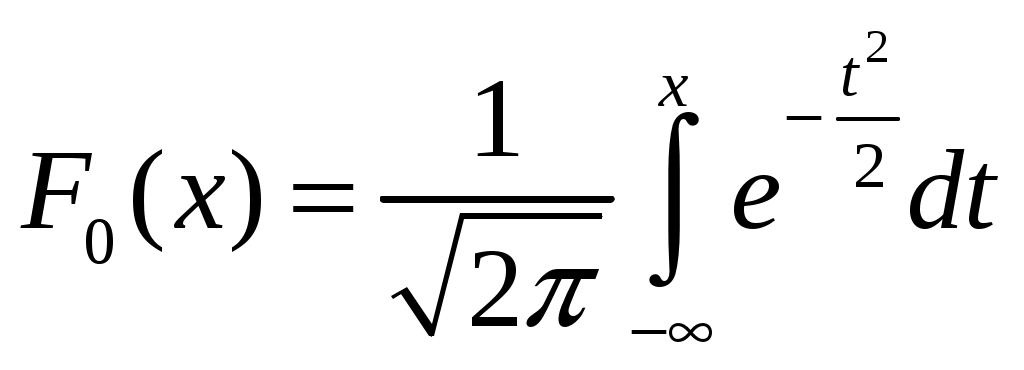 . .Эта функция тоже табулирована. Вероятность попадания нормированной нормальной величины X в интервал (0; x) можно найти, используя функцию Лапласа 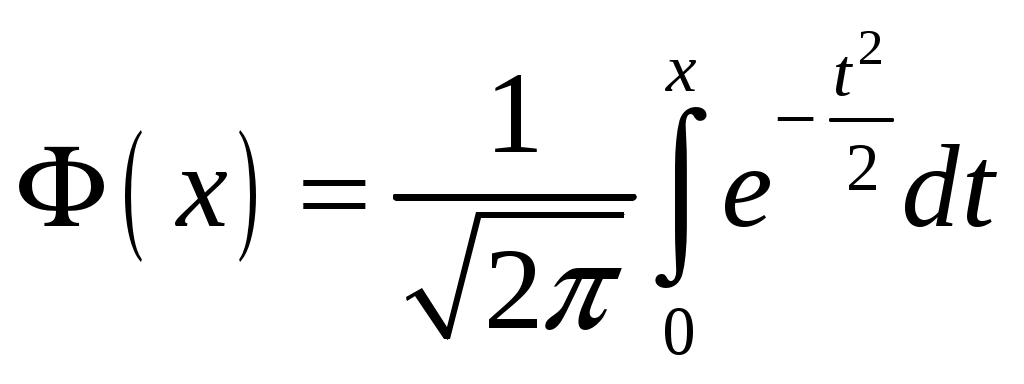 , т.е. покажем, как взаимосвязаны интегральная функция Лапласа и интегральная функция нормированного распределения. , т.е. покажем, как взаимосвязаны интегральная функция Лапласа и интегральная функция нормированного распределения.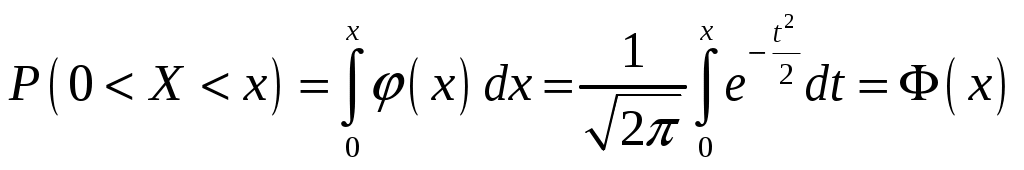 . .Учитывая, что 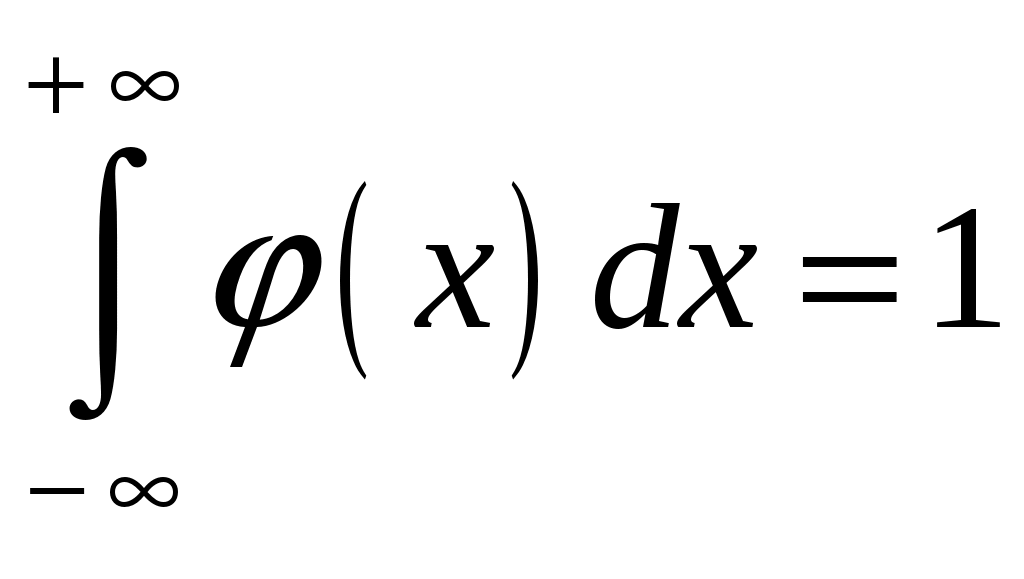 и, следовательно, в силу симметрии (x) относительно нуля, и, следовательно, в силу симметрии (x) относительно нуля, 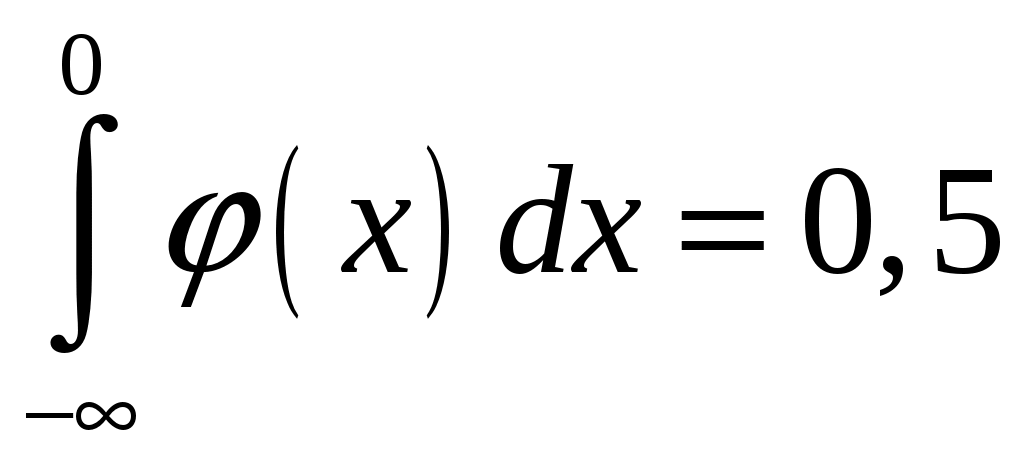 . Значит, . Значит, Тогда Итак, Мы уже знаем, что если случайная величина Xзадана дифференциальной функцией p(x), то вероятность того, что X примет значение, принадлежащее интервалу (a;b), такова: Пусть случайная величина X распределена по нормальному закону. Тогда вероятность того, что X примет значение, принадлежащее интервалу (x1; x2), равна 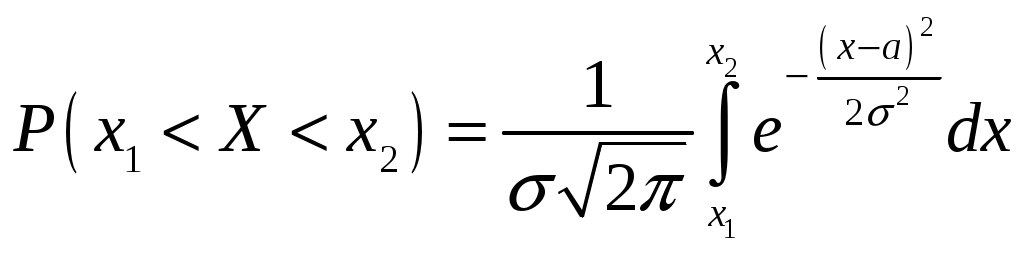 . .Преобразуем эту формулу так, чтобы можно было пользоваться готовыми таблицами. Введем новую переменную Таким образом, имеем 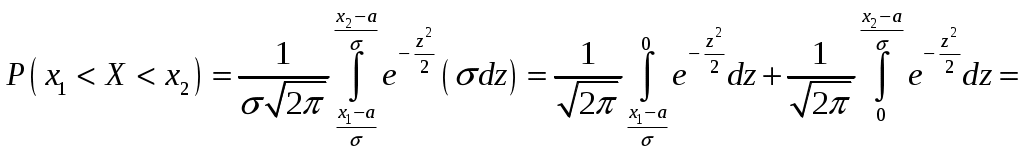 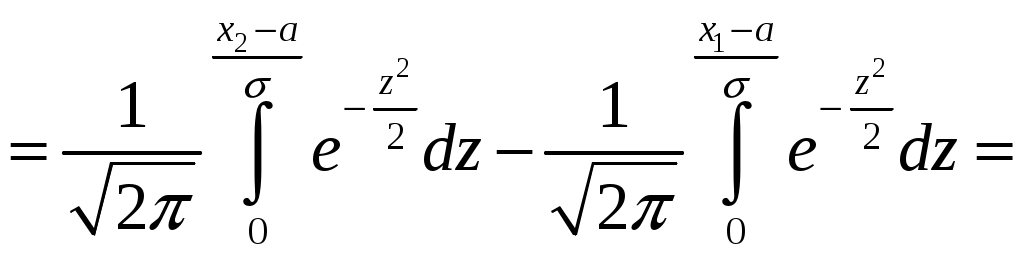 (Воспользуемся функцией Лапласа)= (Воспользуемся функцией Лапласа)=Итак, получаем 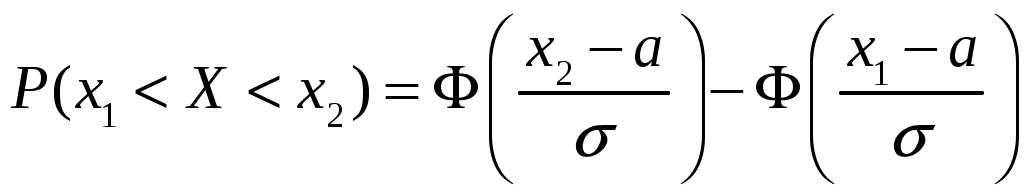 . (2.15) . (2.15)Пример 2.9. Случайная величина Xраспределена по нормальному закону. Математическое ожидание и среднее квадратическое отклонение этой величины соответственно равны 30 и 10. Найти вероятность того, что X примет значение, принадлежащее интервалу (16; 52). Решение. По условию По таблице значений интегральной функции Лапласа определяем Свойства плотности вероятности нормального распределения Рассмотрим свойства плотности вероятности СВ X, распределенных по нормаль-ному закону с параметрами a и . График дифференциальной функции нормального распределения называют нормальной кривой (кривой Гаусса). Исследуем функцию 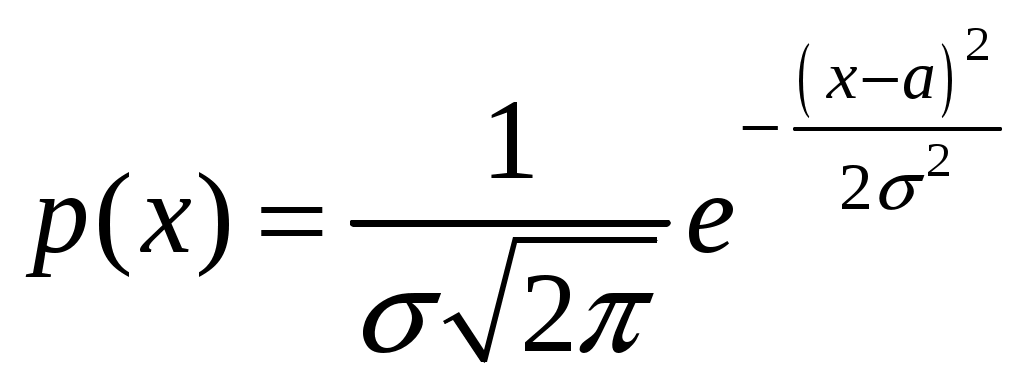 , где >0. , где >0.методом дифференциального исчисления. 1). Функция определена на всей числовой оси Ox., т.е. 2). При всех значениях x функция принимает положительные значения, т.е. нормальная кривая расположена выше оси Ox. 3). 4). Исследуем функцию на экстремум. Найдем первую производную: 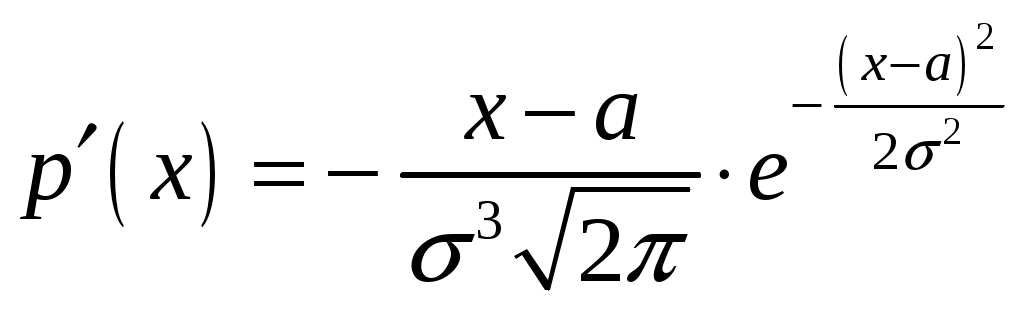 . .Легко видеть, что Следовательно, при x=a функция имеет максимум 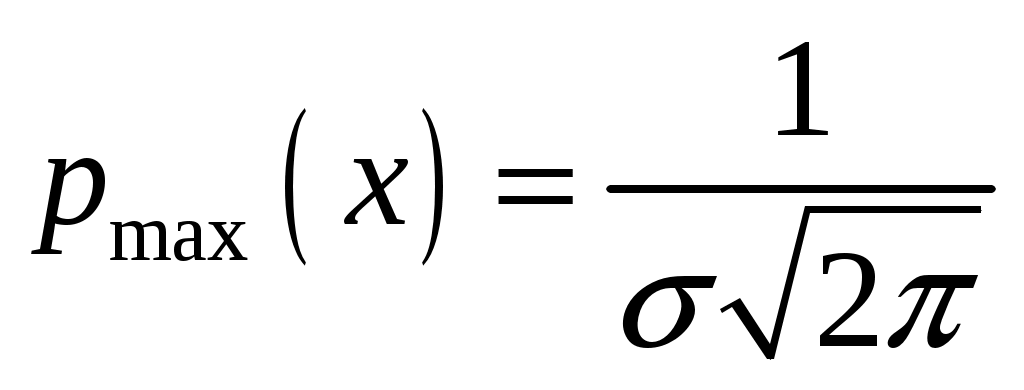 . .5). Разность xa содержится в аналитическом выражении в квадрате, т.е. график функции симметричен относительно прямой x=a. 6). Исследуем функцию на точки перегиба. Найдем вторую производную: 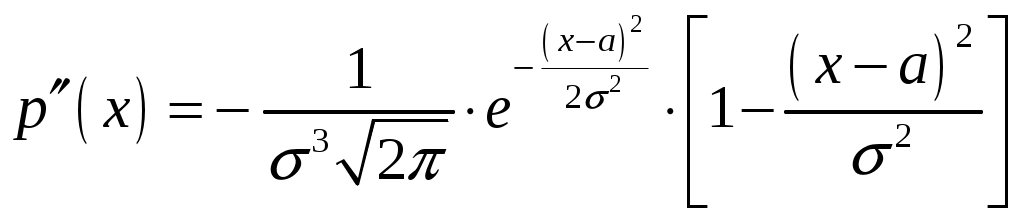 . .Легко видеть, что при x1=a и x2=a+ вторая производная равна нулю, а при переходе через эти точки она меняет знак. Причем значения функции в обеих точках равны 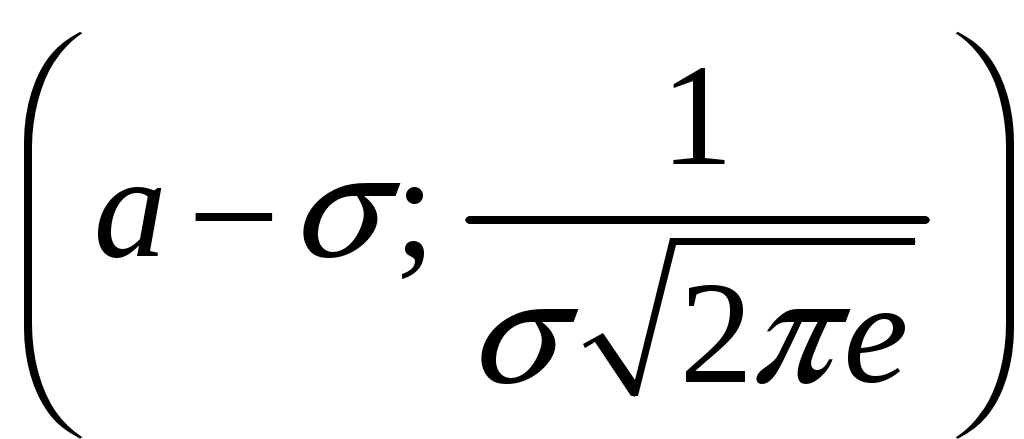 и и 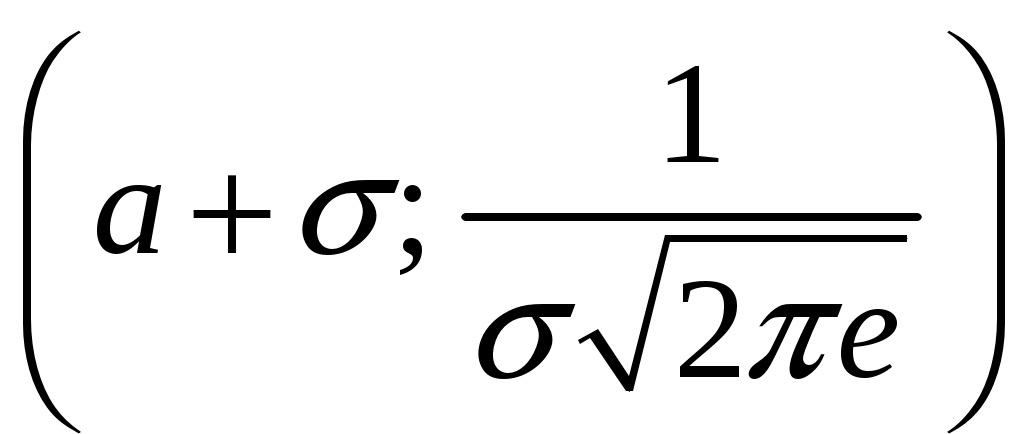 являются точками перегиба. Значит, график функции принимает вид 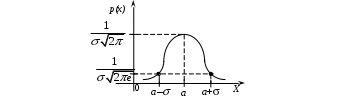 Как видно, на форму и расположение нормальной кривой влияют значения параметров a и . Изменение величины параметра a (математического ожидания) не изменяет формы нормальной кривой, а приводит лишь к ее сдвигу вдоль оси Ox: вправо, если a возрастает и влево, если a убывает. С возрастанием максимальная ордината нормальной кривой убывает, а сама кривая становится более пологой, т.е. сжимается к оси Ox; при убывании нормальная кривая становится более «островершинной» и растягивается в положительном направлении оси Oy. Выше было рассмотрено, как можно найти вероятность того, что СВ X, которая распределена по нормальному закону примет значение, принадлежащее интервалу (x1; x2), и связь с интегральной функцией Лапласа: 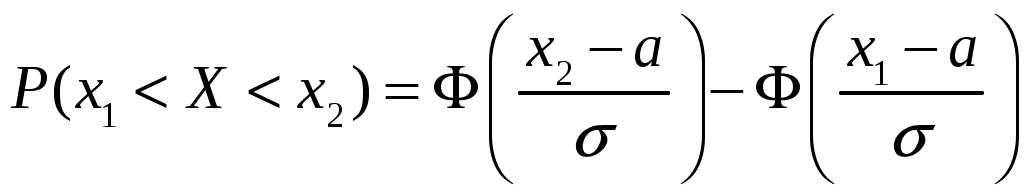 . (*) . (*)Часто на практике требуется вычислить вероятность того, что отклонение нормально распределенной СВ X по абсолютной величине меньше заданного положительного числа , т.е. требуется найти вероятность осуществления неравенства Заменим это неравенство равносильным ему двойным неравенством или Используя формулу (*), получаем 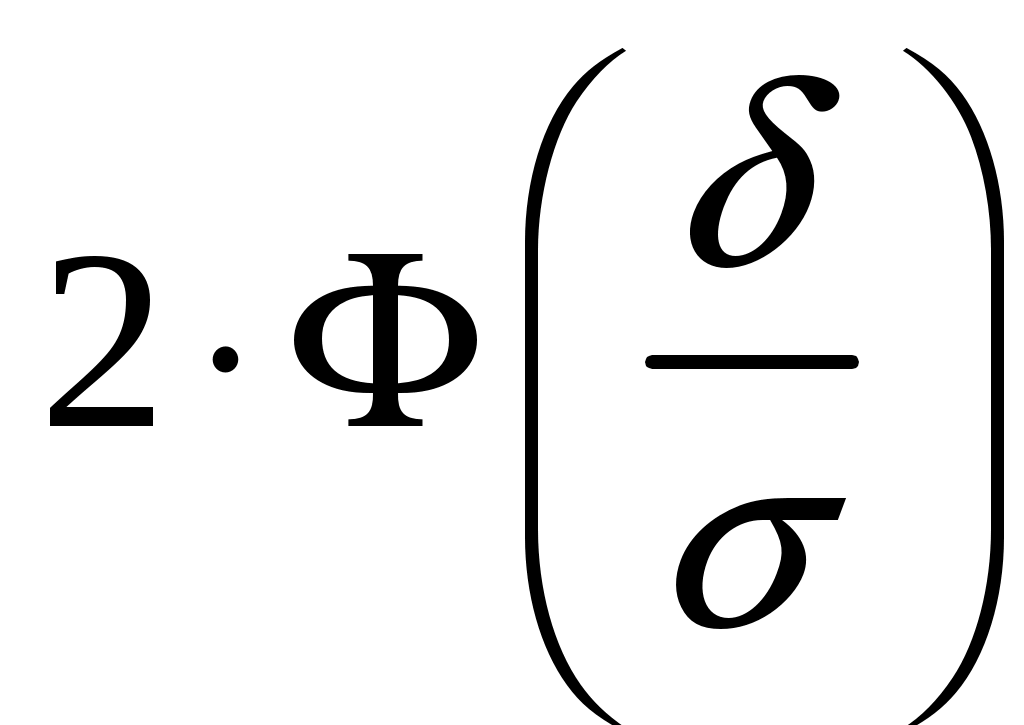 . .Итак, окончательно получаем 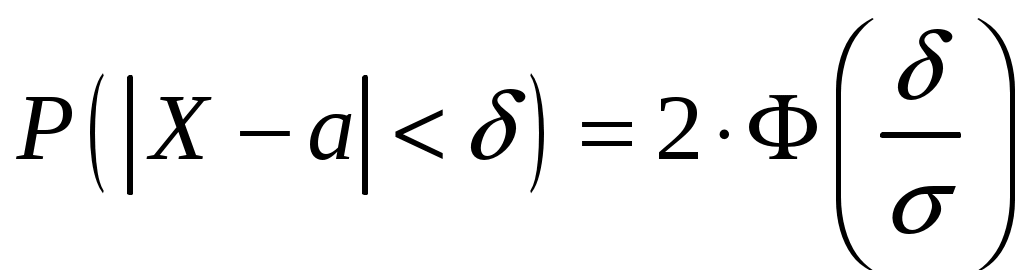 . (2.16) . (2.16)В частности, при |
