математика. РАЗДЕЛ 2 Случайные величины doc. Определение Величина, которая в зависимости от случая может принимать те или другие числовые значения, называется случайной

• Название: Определение Величина, которая в зависимости от случая может принимать те или другие числовые значения, называется случайной
• Анкор: математика
• Дата: 08.05.2022
• Размер: 1.49 Mb.
• Имя файла: РАЗДЕЛ 2 Случайные величины doc.doc
• Тип: Документы; #518007
• страница: 3 из 7

Интегральная и дифференциальная

функции распределения НСВ
Дискретная СВ задается перечнем всех своих возможных значений и их вероятностей. Такой закон распределения ДСВ чаще всего бывает представлен в виде таблицы. Но этот способ не является общим. Он не применим, например, для непрерывной случайной величины, возможные значения которой заполняют некоторый промежуток.

Чтобы задать закон распределения непрерывной СВ вводят интегральную функцию распределения.

Определение 2.1. Интегральной функцией распределения называют функцию , определяющую для каждого значения вероятность того, что случайная величина примет значение, меньшее , т.е.

. (2.1)
Геометрически это равенство можно истолковать так: есть вероятность того, что случайная величина примет значение, которое изображается на числовой оси точкой, лежащей левее точки .

Теперь можно дать более точное определение непрерывной случайной величины.

Определение 2.2. Случайная величина называется непрерывной, если ее интегральная функция распределения непрерывно дифференцируемая.

Рассмотрим свойства интегральной функции распределения непрерывной СВ, которые примем без доказательства.
Свойства интегральной функции НСВ
Свойство 1. Значения интегральной функции принадлежит отрезку 0; 1, т.е.

.
Свойство 2. – неубывающая функция, т.е.

.
Свойство 3. Функция распределения непрерывна слева, т.е.

.

Свойство 4. Если возможные значения непрерывной случайной величины расположены на всей числовой оси , то справедливы следующие предельные соотношения:

.
Из свойства 2 вытекают два следствия, которые примем без доказательства.

Следствие 2.1. Вероятность того, что случайная величина примет значение, заключенное в интервале , равна приращению интегральной функции на этом интервале:

. (2.2)
Следствие 2.2. Вероятность того, что непрерывная случайная величина X примет одно определенное значение, равно нулю, т.е.

.
Выше дали определение непрерывной случайной величины, как случайной величины, функция распределения которой непрерывно дифференцируемая. В этом случае имеет производную, которую обозначим через , т.е. . Выясним вероятностный смысл функции . Возьмем какой-нибудь полуинтервал . Вероятность попадания значения на этот полуинтервал, т.е. , равна (следствие 2.1.):

.

Если правую и левую части этого равенства разделить на длину полуинтервала , получим

.

Левая часть – это отношение вероятности попадания значения случайной величины X на полуинтервал к длине этого полуинтервала, которое называют средней плотностью распределения вероятностей на полуинтервале . Если перейти к пределу при , получим

.
Предел средней плотности равен , и его называют плотностью распределения (дифференциальной функцией распределения) случайной величины X.
Определение 2.3. Дифференциальной функцией распределения (плотностью распределения) называют первую производную от интегральной функции:

. (2.3)
Рассмотрим свойства дифференциальной функции распределения непрерывной случайной величины, которые примем без доказательства.
Свойства дифференциальной функции НСВ
Свойство 1. Дифференциальная функция неотрицательна, т.е.

.
Свойство 2. Несобственный интеграл от дифференциальной функции в пределах от 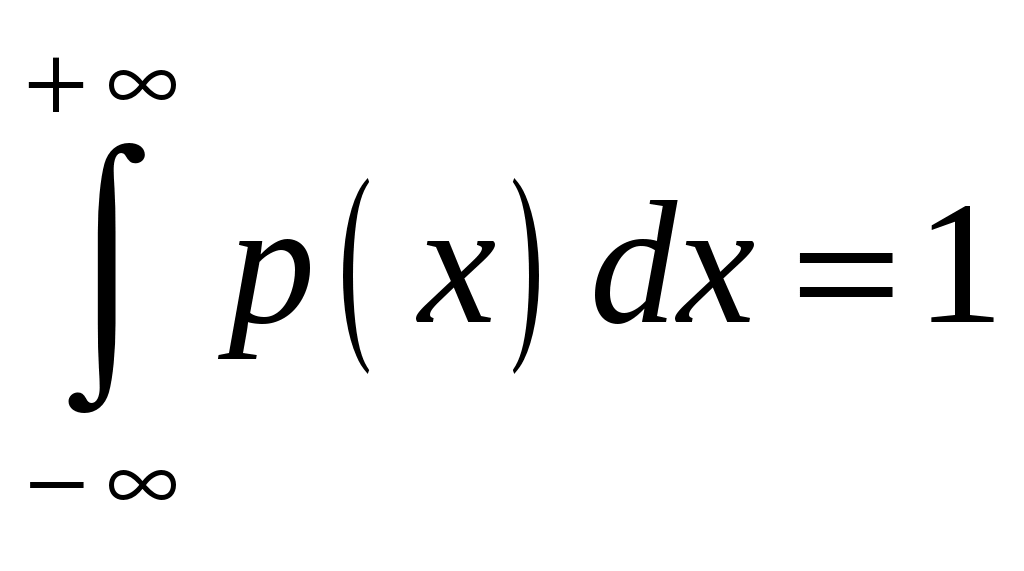до равен единице:

. (2.4)
Теорема 2.1. Вероятность того, что непрерывная случайная величина примет значение, принадлежащее интервалу 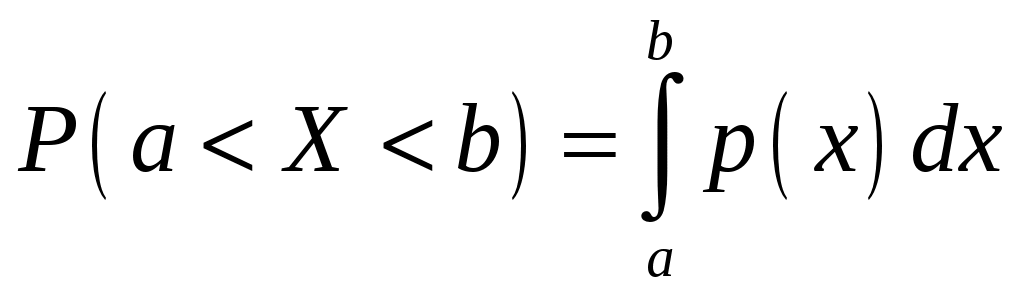, равна определенному интегралу от дифференциальной функции, взятому в пределах от до :

. (2.5)
Следствие 2.3. Если 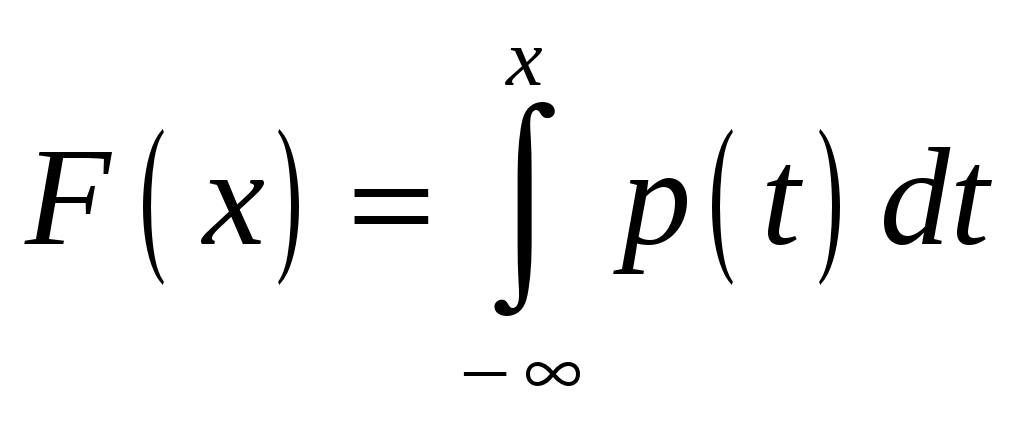 плотность распределения вероятностей, то интегральную функцию распределения можно найти по формуле

. (2.6)
График функции называют кривой плотности распределения случайной величины или просто кривой вероятностей. Отметим особенности, которые присущи любой кривой вероятности:

1) она всегда лежит в верхней координатной полуплоскости;

2) площадь, заключенная между этой кривой и осью абсцисс, равна 1.

Вероятность того, что случайная величина 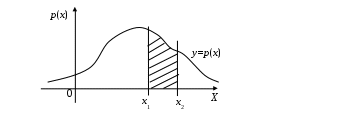примет значение, заключенное между и – это площадь заштрихованной криволинейной трапеции.


Пример 2.1. Дана функция распределения 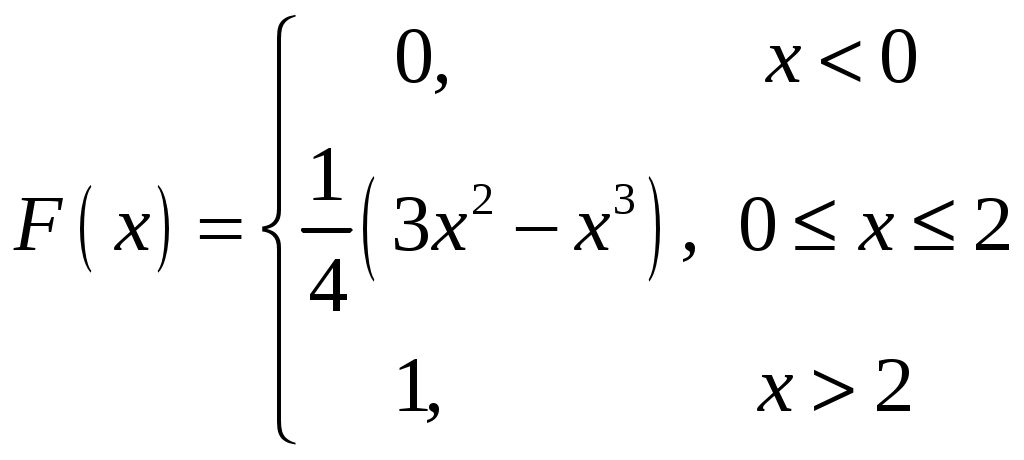СВ X:

.

Найти плотность распределения . Построить графики функций и . Найти вероятность попадания СВ X на отрезок .

Решение. 1) Чтобы найти плотность вероятности, воспользуемся формулой 2.3. Тогда получаем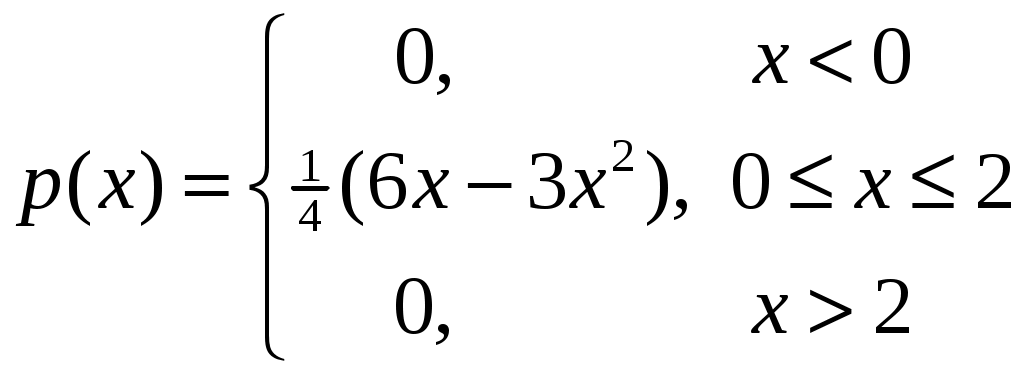

.
2) Строим графики функций и

3) Находим вероятность попадания СВ X на отрезок 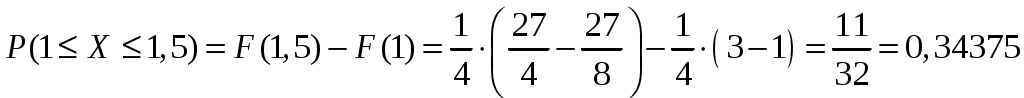, используя формулу 2.2. (Отметим то, что для нахождения вероятности попадания СВ X на отрезок можно воспользоваться формулой 2.5).

.



Пример 2.2. Найти интегральную функцию по данной дифференциальной функции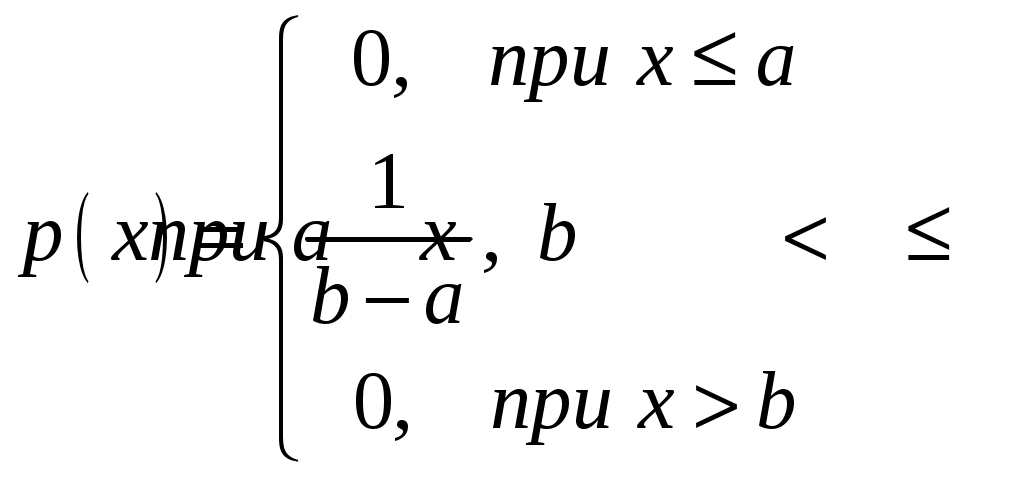

.

Решение. Чтобы найти интегральную функцию распределения, воспользуемся формулой 2.6.

Если 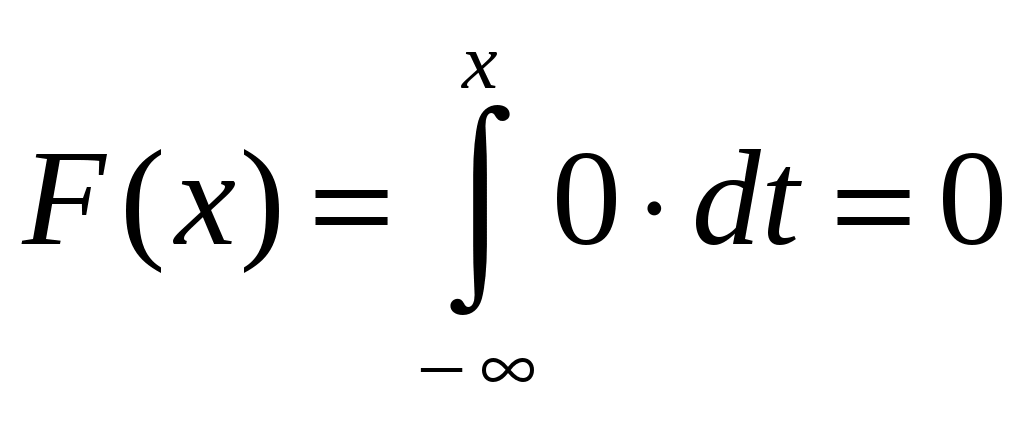, то .

Если 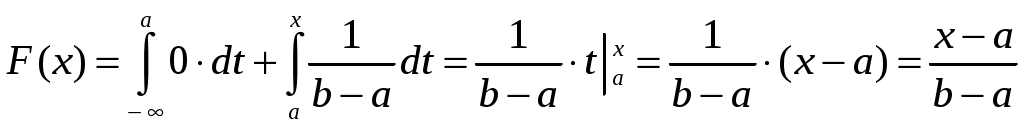, то

.

Если 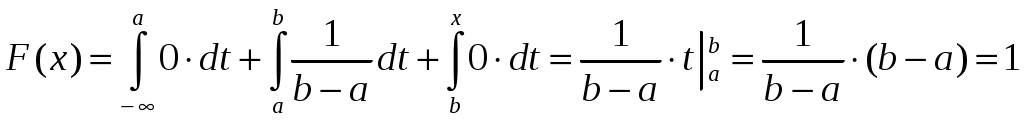, то

.

Следовательно, получаем следующую интегральную функцию распределения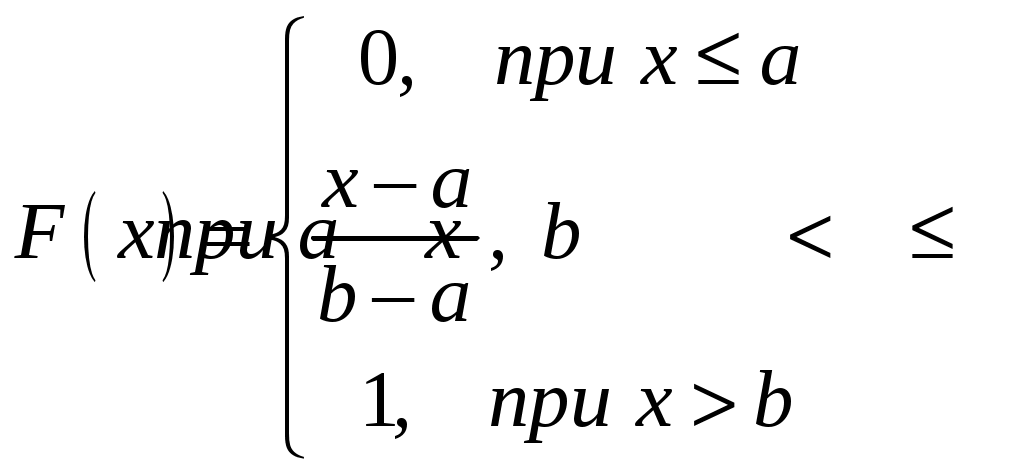

.



2. 
   Числовые характеристики НСВ
   

Рассмотрим числовые характеристики для непрерывной случайной величины.
Начнем с математического ожидания.
Пусть непрерывная случайная величина 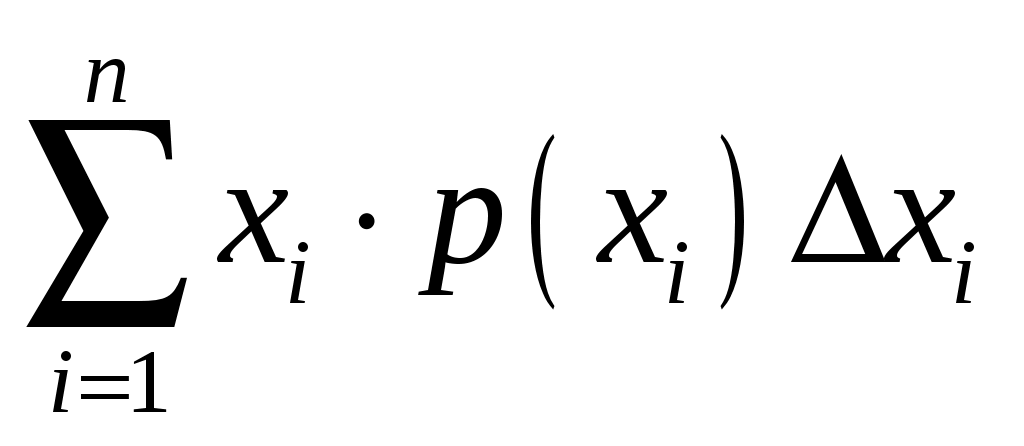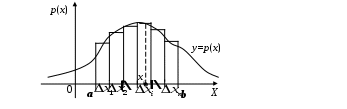задана дифференциальной функцией . Допустим, что все возможные значения принадлежат отрезку . Разобьем этот отрезок на n частичных отрезков длиною и выберем в каждом из них произвольную точку . Имея в виду задачу: определить математическое ожидание непрерывной величины по аналогии с дискретной, составим сумму произведений возможных значений x_i на вероятности попадания их в интервал (напомним, что произведение приближенно равно вероятности попадания в интервал ):

.


Перейдем к пределу при стремлении к нулю длины наибольшего из частичных отрезков, т.е. 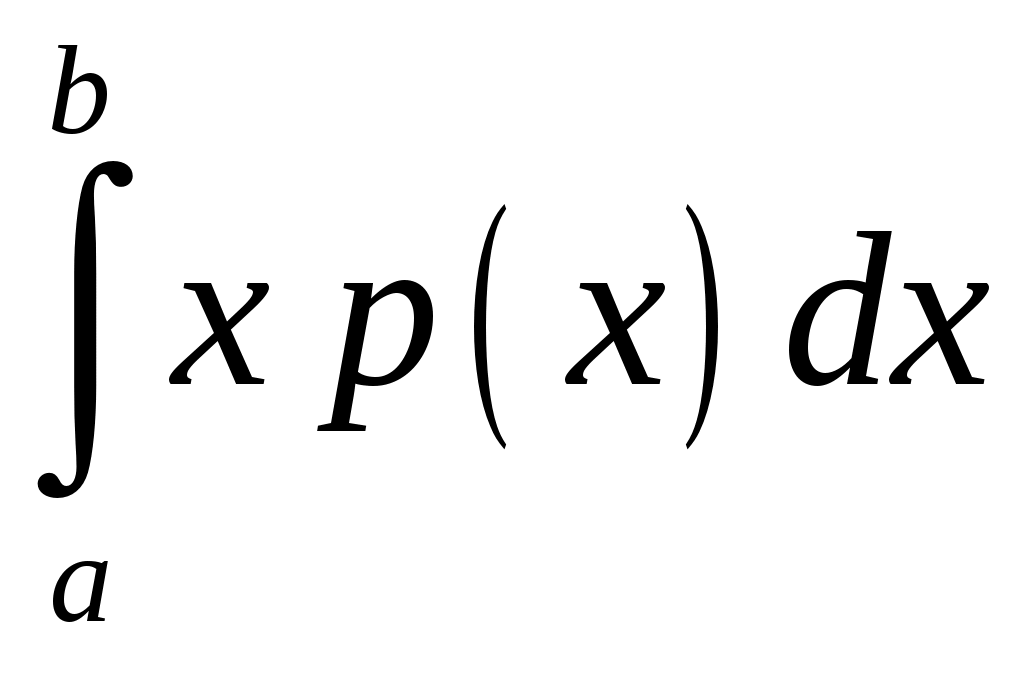. Так как – непрерывная функция, то существует и равен .

Определение 2.4. Математическим ожиданием непрерывной случайной величины 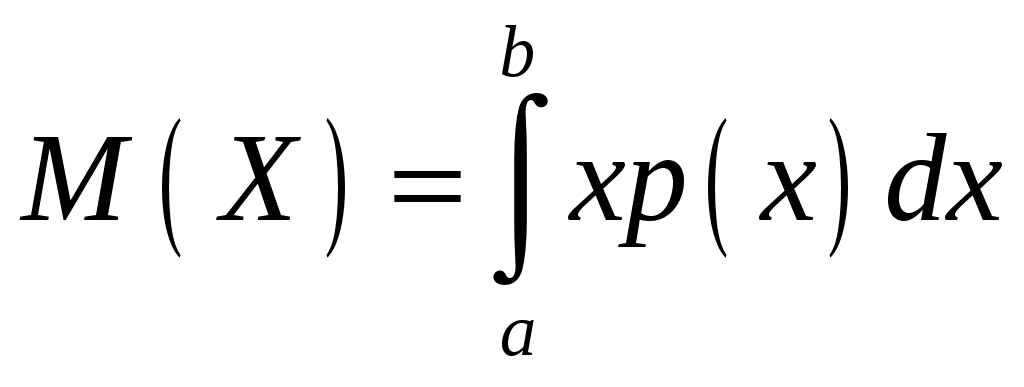, возможные значения которой принадлежат отрезку , называют определенный интеграл:

. (2.7)
Если возможные значения принадлежат всей числовой оси Ox, то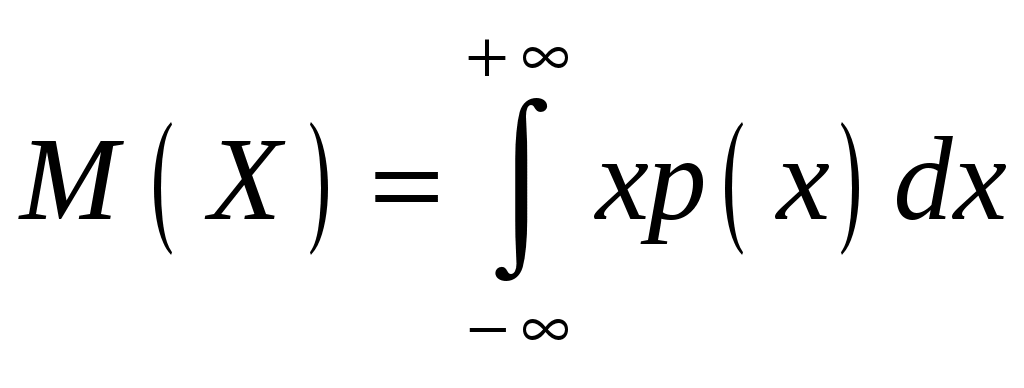

. (2.8)
По аналогии с дисперсией дискретной величины определяется дисперсия непрерывной величины.
Определение 2.5. Дисперсией непрерывной случайной величины называют математическое ожидание квадрата ее отклонения.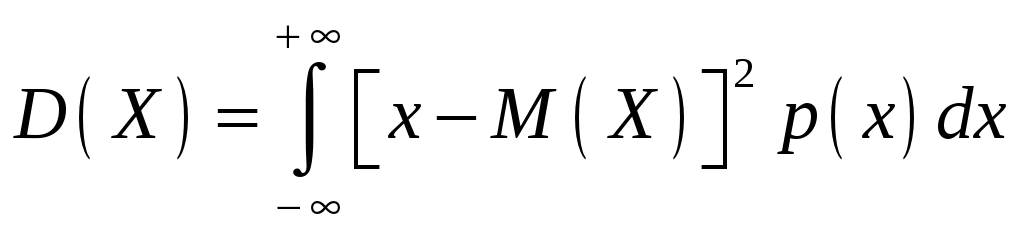

. (2.9)
Но для вычисления дисперсии лучше использовать следующую формулу: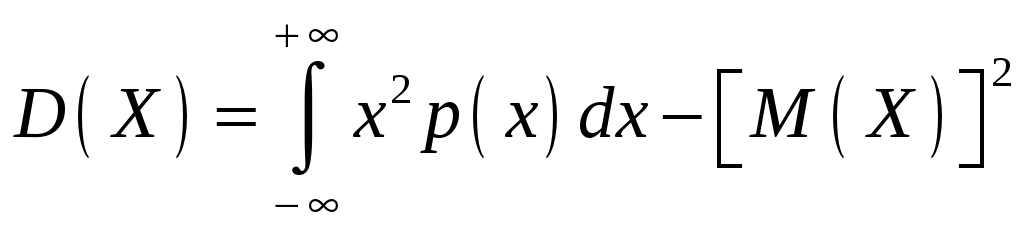

. (2.10)
Определение 2.6. Средним квадратическим отклонением непрерывной СВ X называют квадратный корень из дисперсии:

. (2.11)

Кстати, можно доказать, что свойства математического ожидания и дисперсии дискретных величин сохраняются и для непрерывных величин.
Определение 2.7. Модой непрерывной случайной величины называют такое ее значение M_o, при котором плотность распределения вероятности достигает максимум.
Определение 2.8. Медианой непрерывной случайной величины называют такое ее значение M_е, относительно которого равновероятно получение большего или меньшего значения случайной величины X, т.е.

.

Геометрический смысл M_е: M_е – это абсцисса точки, в которой площадь фигуры, ограниченной кривой , делится пополам.
Пример 2.3. Дана функция распределения 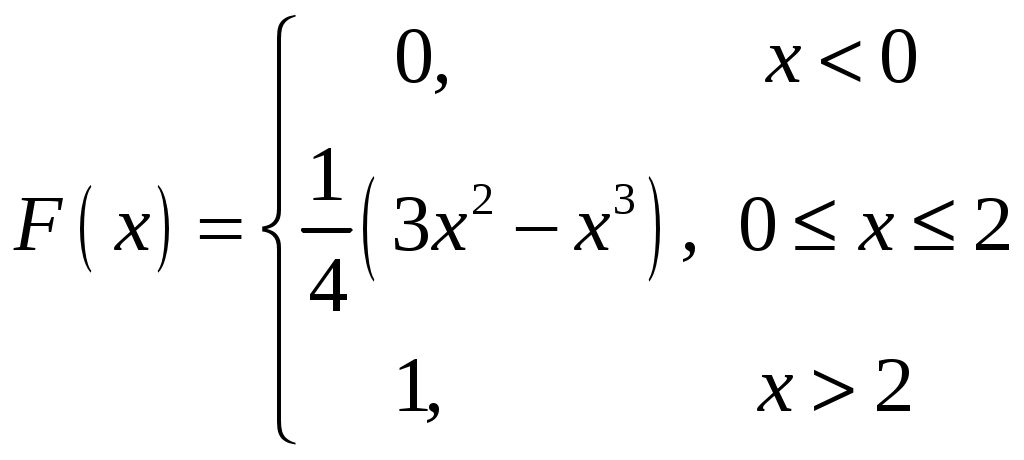СВ X:

.

Найти числовые характеристики СВ X:

Решение. В примере 2.1. для данной интегральной функции распределения была найдена дифференциальная функция распределения. Запишем ее: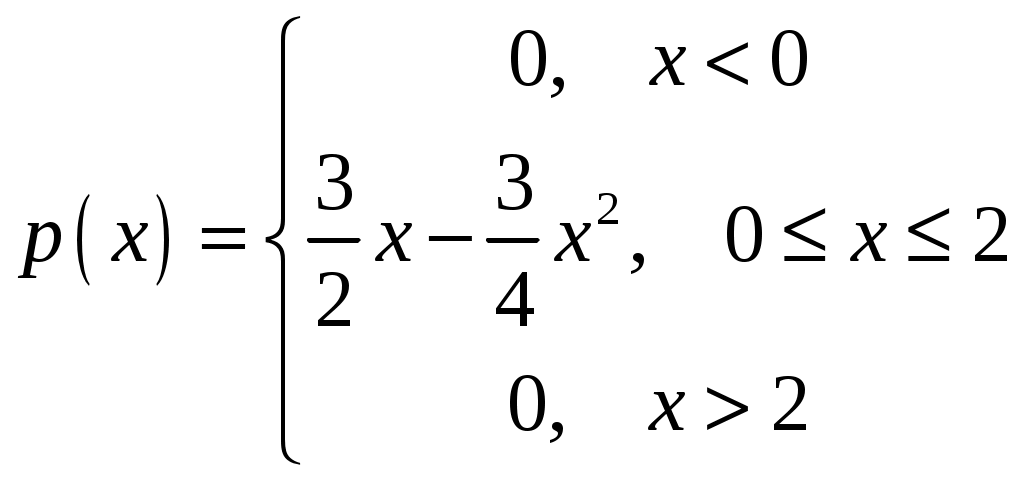

.

Далее последовательно вычисляем:

1) .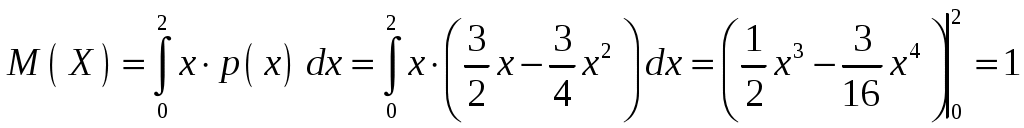
2) ,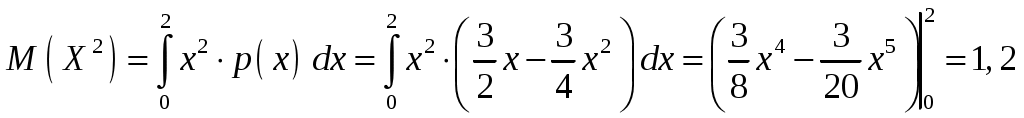
.
3) .
4) Согласно определению 2.7. находим производную функции плотности распределения вероятности.

,

.

В точке функция достигает максимума, значит, .
5) Найдем медиану НСВ X, используя формулу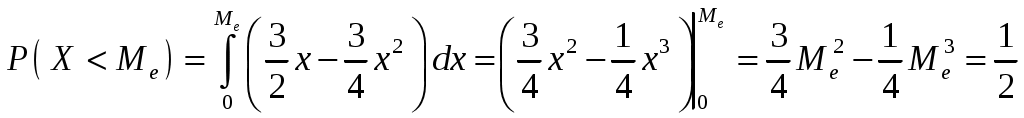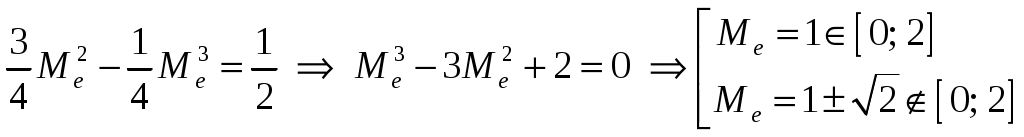

.
.
.

Итак, .

