|
|
математика. РАЗДЕЛ 2 Случайные величины doc. Определение Величина, которая в зависимости от случая может принимать те или другие числовые значения, называется случайной
Пример 4.3. Сколько раз нужно измерить данную величину, истинное значение которой равно  , чтобы с вероятностью, не меньшей, чем 0,95, можно было утверждать, что среднее арифметическое значение этих измерений отличается от , чтобы с вероятностью, не меньшей, чем 0,95, можно было утверждать, что среднее арифметическое значение этих измерений отличается от  по абсолютной величине меньше, чем на 3, если среднее квадратическое отклонение каждого из измерений меньше 12? по абсолютной величине меньше, чем на 3, если среднее квадратическое отклонение каждого из измерений меньше 12?
Решение. Пусть 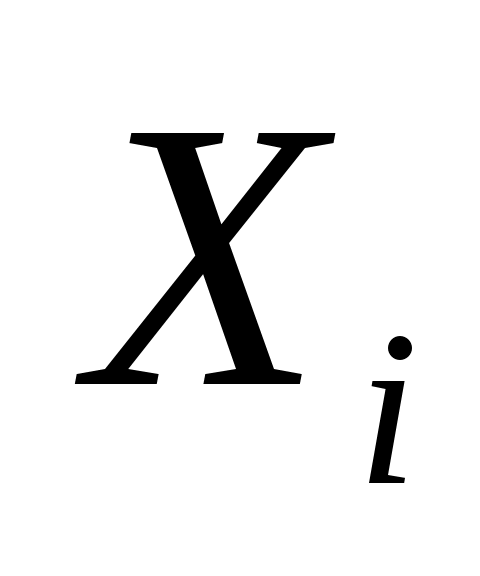 – результат i-го измерения. Из условия задачи следует, что – результат i-го измерения. Из условия задачи следует, что 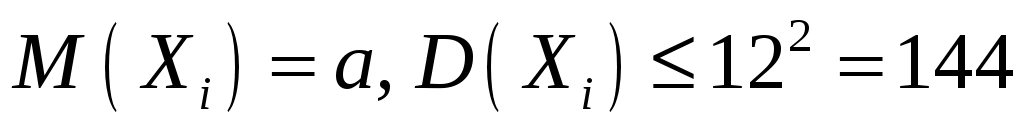 . Поэтому . Поэтому
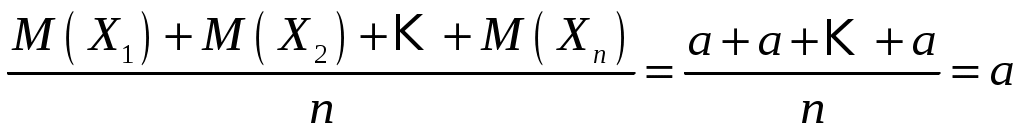 . .
Найдем число n, при котором
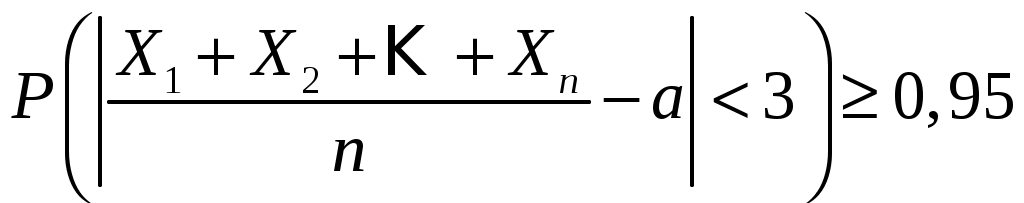 . .
Так как
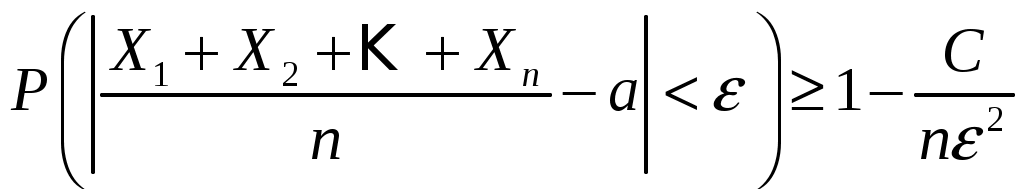
где  , то это неравенство, во всяком случае, будет выполняться, если , то это неравенство, во всяком случае, будет выполняться, если
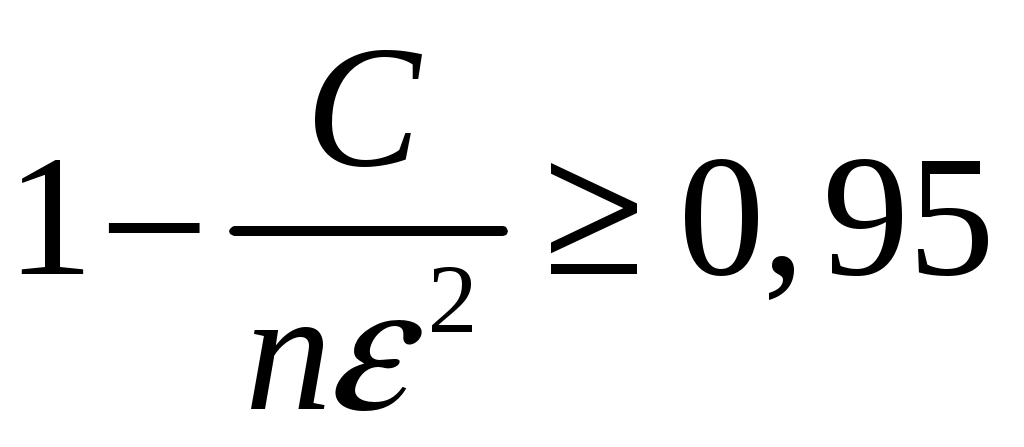
Отсюда
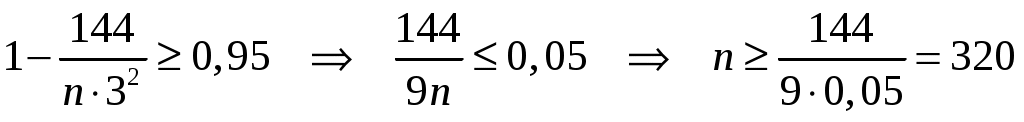 . .
Итак, достаточно сделать 320 измерений данной величины.
Пусть производится 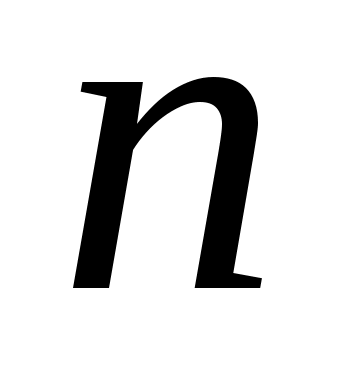 независимых испытаний, в каждом из которых вероятность появления события независимых испытаний, в каждом из которых вероятность появления события  равна равна 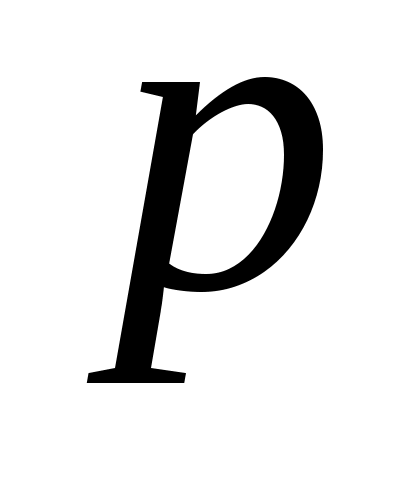 . Можно ли предвидеть: какой будет относительная частота появлений события? Положительный ответ на этот вопрос дает теорема, доказанная Яковом Бернулли (опубликованная в 1713 г.), которая получила название «закона больших чисел» и положила начало теории вероятностей как науке. Доказательство Я. Бернулли было сложным; простое доказательство дано П.Л. Чебышевым в 1846 г. Сформулируем теорему Бернулли без доказательства. . Можно ли предвидеть: какой будет относительная частота появлений события? Положительный ответ на этот вопрос дает теорема, доказанная Яковом Бернулли (опубликованная в 1713 г.), которая получила название «закона больших чисел» и положила начало теории вероятностей как науке. Доказательство Я. Бернулли было сложным; простое доказательство дано П.Л. Чебышевым в 1846 г. Сформулируем теорему Бернулли без доказательства.
Теорема 4.4 (теорема Бернулли).
Если в каждом из 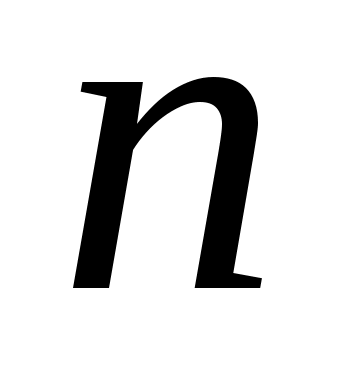 независимых испытаний вероятность независимых испытаний вероятность 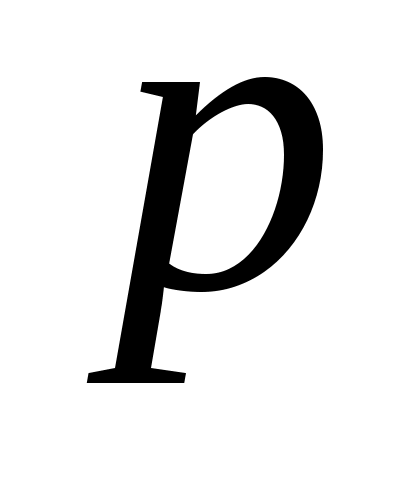 появления события появления события  постоянно, то как угодно близка к единице вероятность того, что отклонение относительной частоты от вероятности постоянно, то как угодно близка к единице вероятность того, что отклонение относительной частоты от вероятности 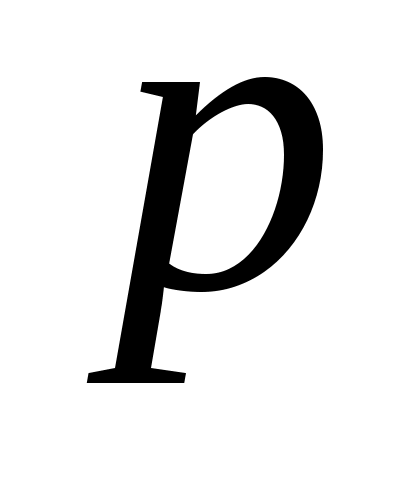 будет меньше по модулю положительного числа , если число испытаний достаточно велико будет меньше по модулю положительного числа , если число испытаний достаточно велико
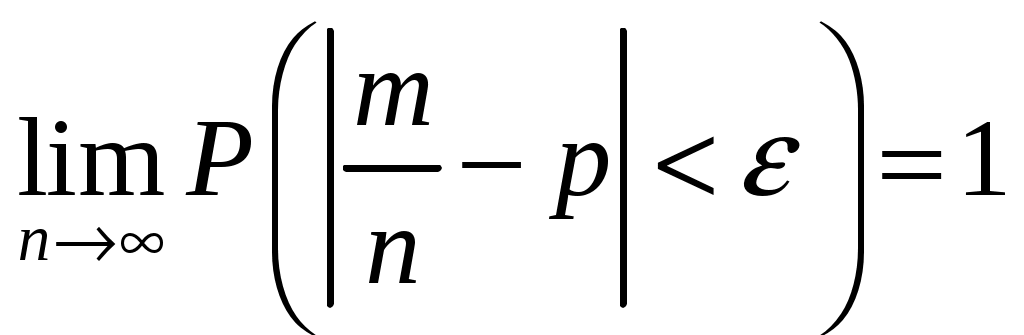 . (4.8) . (4.8)
Было бы неправильным на основании теоремы Бернулли сделать вывод, что с ростом испытаний относительная частота неуклонно стремится к вероятности 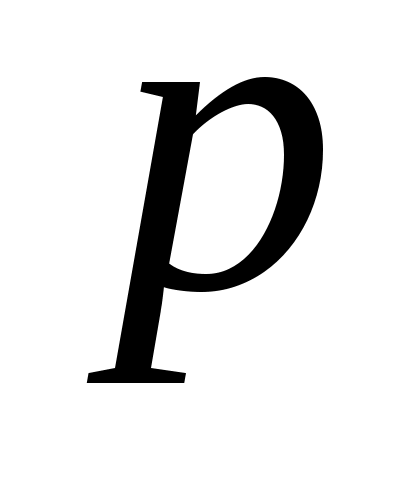 ; другими словами, из теоремы Бернулли не вытекает равенство ; другими словами, из теоремы Бернулли не вытекает равенство 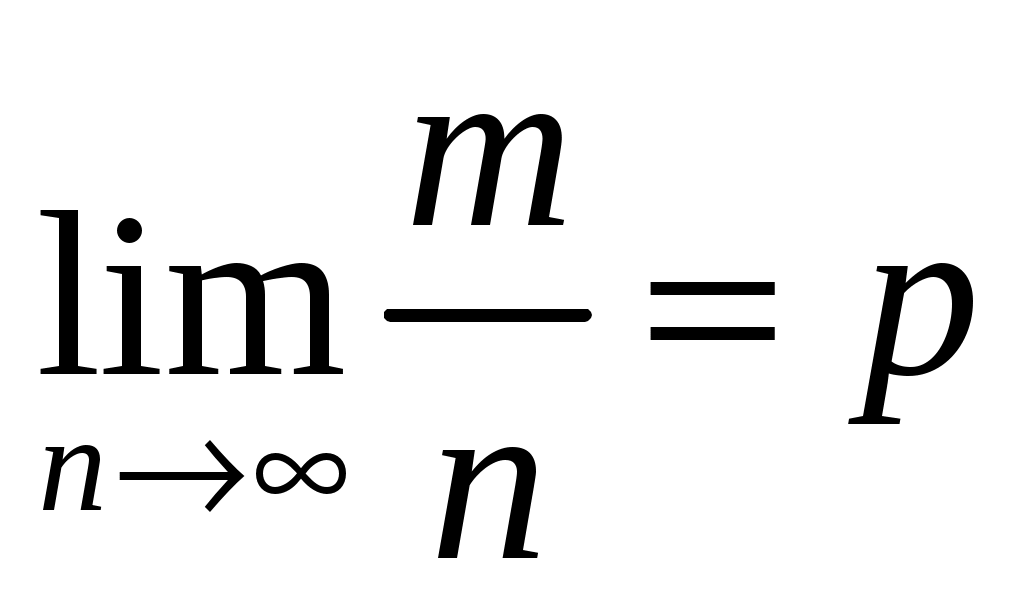 . В теореме речь идет лишь о вероятности того, что при достаточно большом числе испытаний относительная частота будет как угодно мало отличаться от постоянной вероятности появления события в каждом испытании. . В теореме речь идет лишь о вероятности того, что при достаточно большом числе испытаний относительная частота будет как угодно мало отличаться от постоянной вероятности появления события в каждом испытании.
Таким образом, сходимость относительной частоты 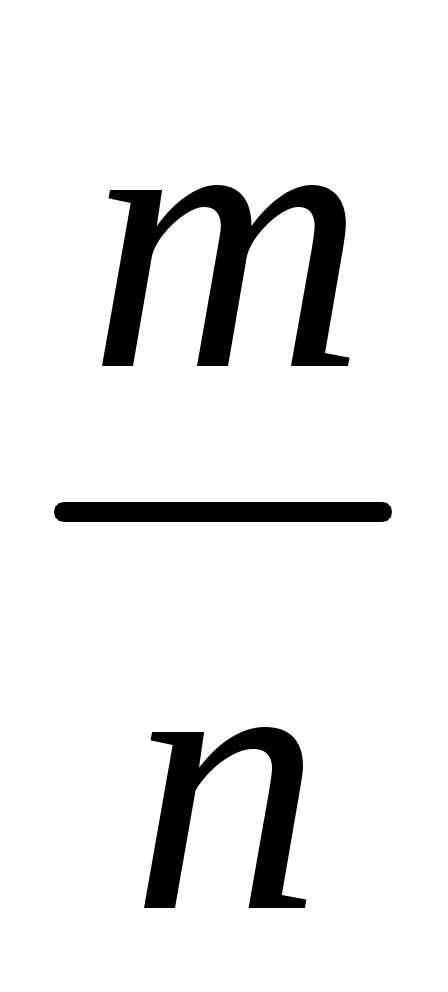 к вероятности к вероятности 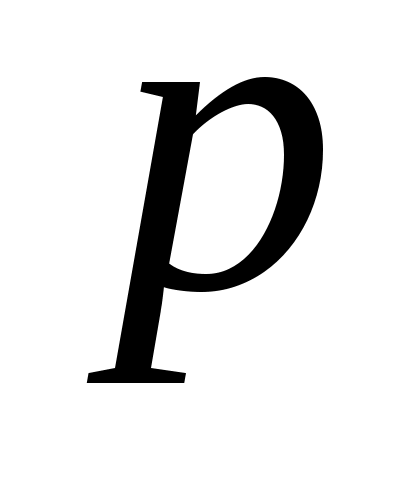 отличается от сходимости в смысле обычного анализа. Для того чтобы подчеркнуть это различие, вводят понятие «сходимости по вероятности». Точнее, различие между указанными видами сходимости состоит в следующем: если отличается от сходимости в смысле обычного анализа. Для того чтобы подчеркнуть это различие, вводят понятие «сходимости по вероятности». Точнее, различие между указанными видами сходимости состоит в следующем: если 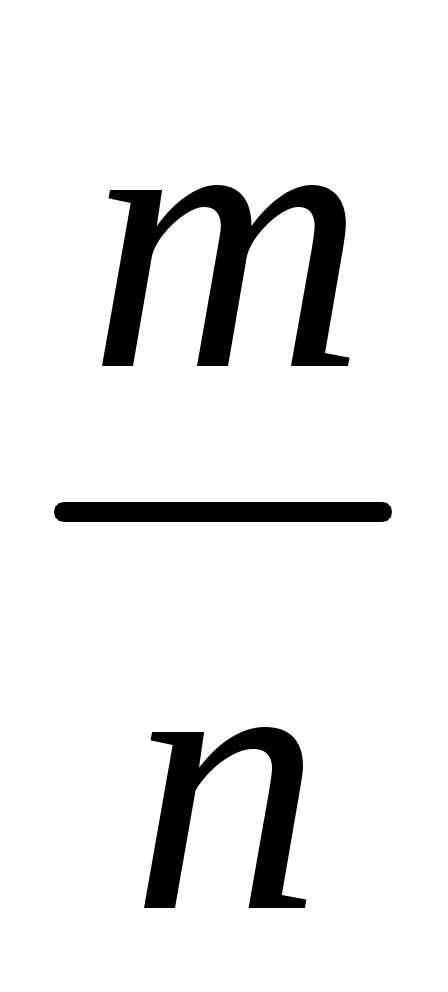 стремится при стремится при  к к 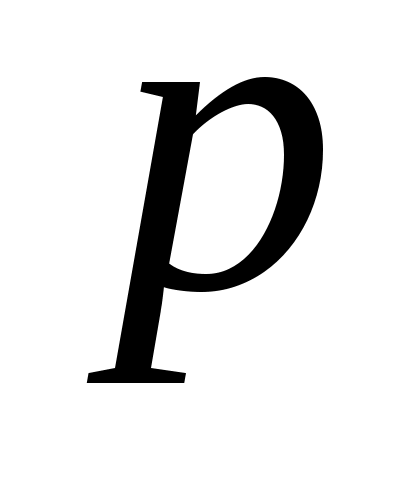 как пределу в смысле обычного анализа, то, начиная с некоторого как пределу в смысле обычного анализа, то, начиная с некоторого 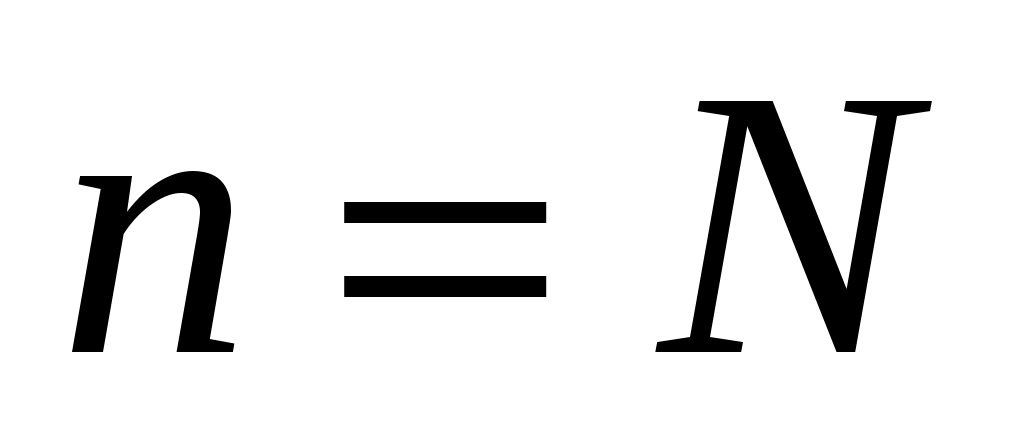 и для всех последующих значений и для всех последующих значений 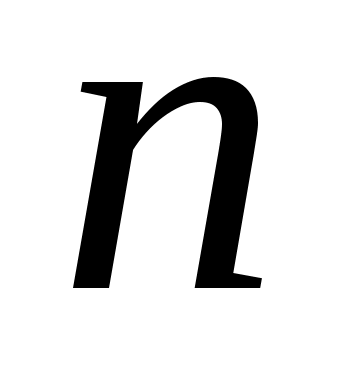 , неуклонно выполняется неравенство , неуклонно выполняется неравенство 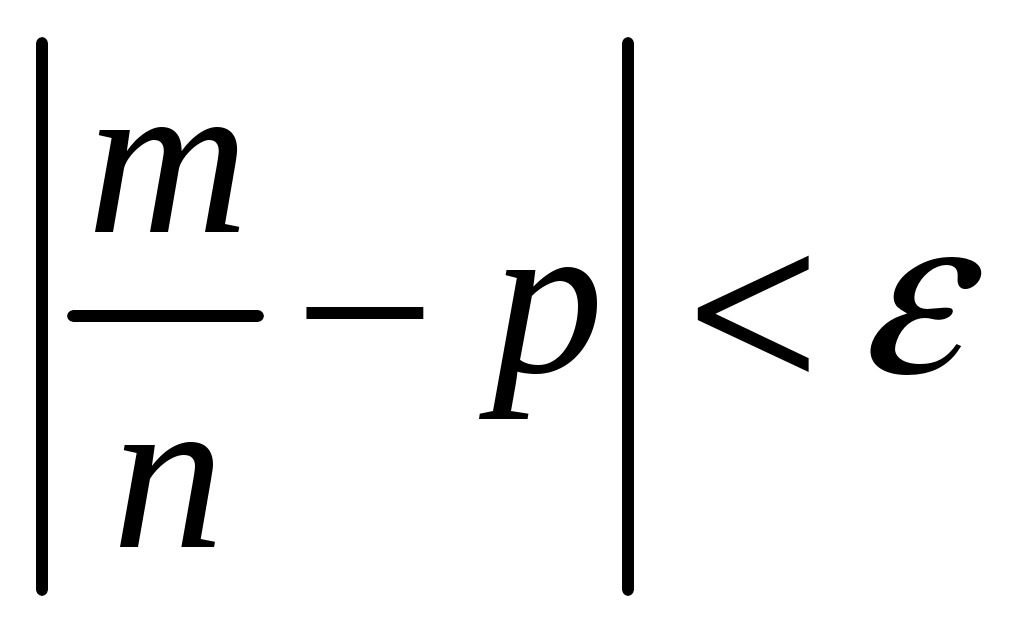 ; если же ; если же 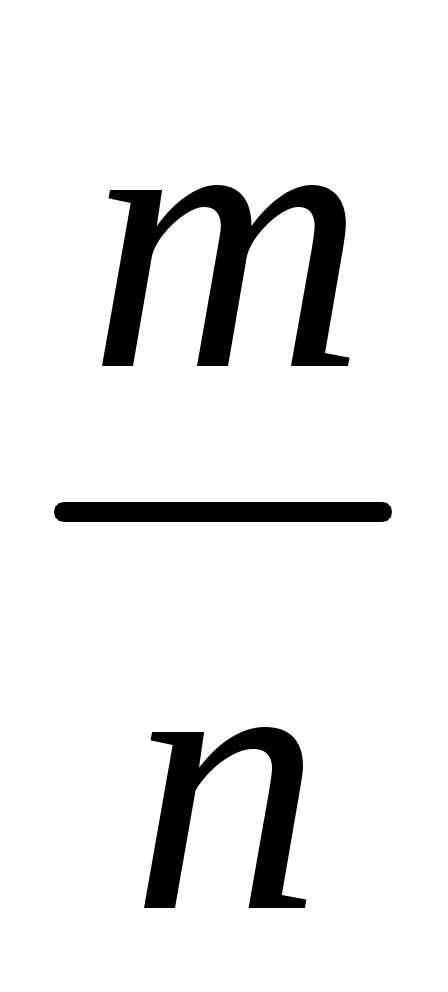 стремится по вероятности к стремится по вероятности к 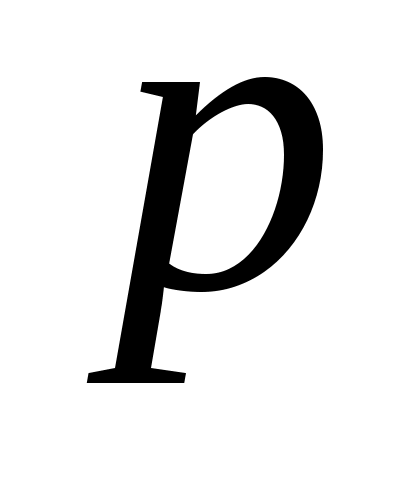 при при  , то для отдельных значений , то для отдельных значений 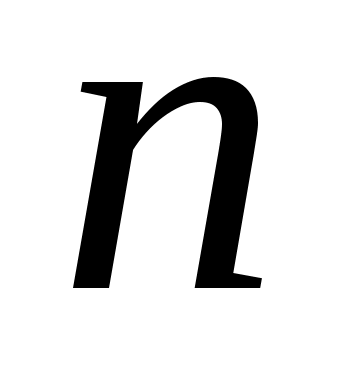 неравенство может не выполняться. неравенство может не выполняться.
Итак, теорема Бернулли утверждает, что при  относительная частота стремится по вероятности к относительная частота стремится по вероятности к 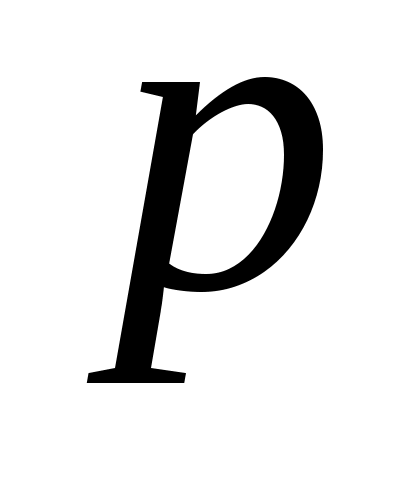 . Коротко теорему Бернулли записывают так: . Коротко теорему Бернулли записывают так:
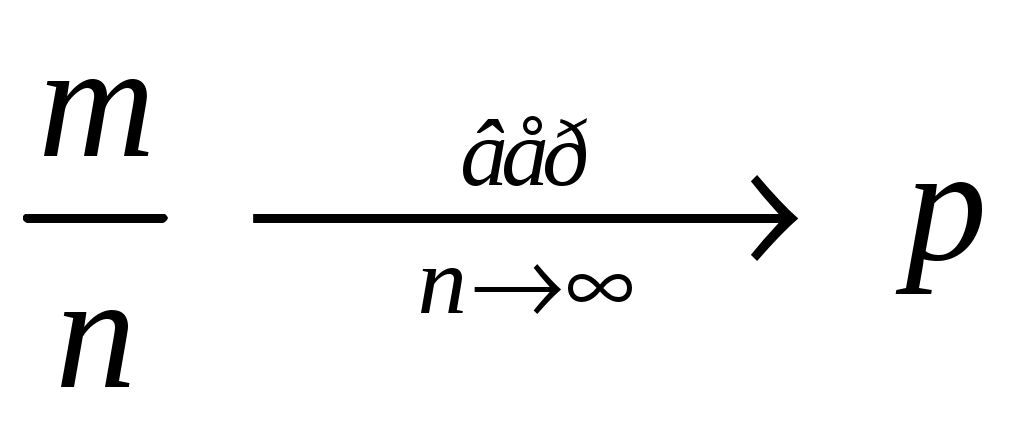 . . |
|
|
 Скачать 1.49 Mb.
Скачать 1.49 Mb.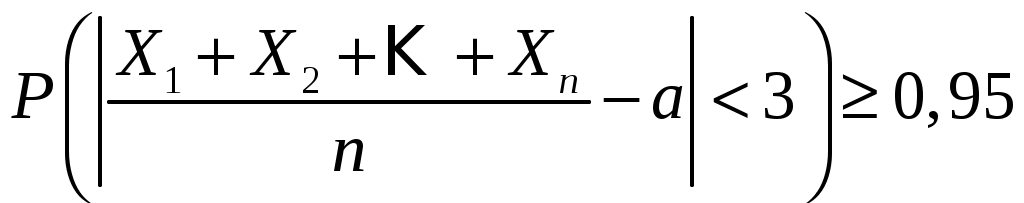 .
.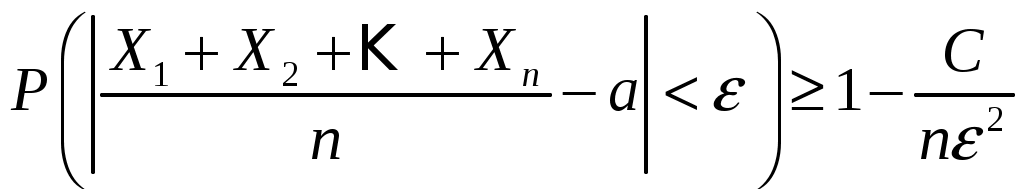
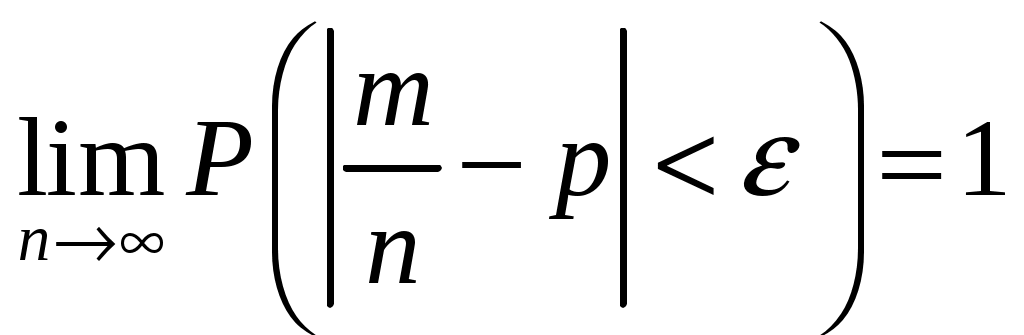 . (4.8)
. (4.8)