Теоретическая справка для кинематики ЕГЭ. Кинематика ЕГЭ. Основы кинематики
 Скачать 0.6 Mb. Скачать 0.6 Mb.
|
|
Основы кинематики Кинематика – раздел механики, в котором изучается процесс движения тел (материальных точек); Перейдем к изучению структуры кинематики. Поскольку основным процессом, который изучается в кинематике, является движение, то необходимо разобраться, что это, и каким образом можно его описать. Движение – изменение местоположения предмета в пространстве с течением времени. Таким образом, появляется необходимость в определении местоположения предмета в различные моменты времени. Это возможно сделать с введением понятия координаты. Координата – местоположение точки/ предмета на линии/плоскости относительно определенного нуля (начала отсчета, начального местоположения). Существуют различные системы координат, однако, мы остановимся на одной, называемой Декартовой. Обратите внимание на рисунок ниже. 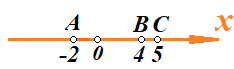 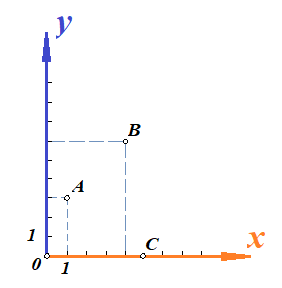 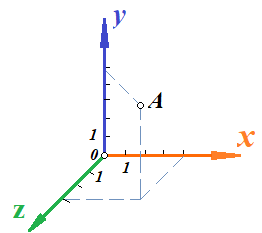 Крайний рисунок слева – линейная система координат, состоящая из одной единственной оси 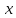 . Очевидно, что координаты точек есть . Очевидно, что координаты точек есть 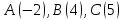 . . Центральный рисунок – плоская система координат, где положение каждой точки определяется двумя координатами – 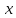 и и 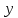 . Очевидно, что координаты точек есть . Очевидно, что координаты точек есть 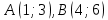 . .Крайний рисунок справа – объемная система координат, где положение каждой точки определяется тремя координатами - 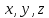 . Очевидно, координата точки . Очевидно, координата точки 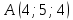 . .Из всего сказанного выше ясно, что движущийся предмет изменяет свое положение в пространстве. Используя понятие функции, разберемся, как это возможно представить аналитически. Нами было дано определение понятия движения как изменение положения предмета в пространстве (координаты предмета) с течением времени. Почему нам недостаточно знать только начальное и конечное положение предмета? Для чего нам требуется работать именно с зависимостью координаты от времени (то есть требуется знание того, где находился предмет в каждый момент времени движения? Представьте, что мы не использовали прибор, измеряющий время. Тогда, если мы, зная первоначальное положение предмета, увидим только его конечное положение (минуя все предыдущие), нам не удастся восстановить картину его движения. Для наглядности, приведем рисунок, на котором нам известны начальное положение предмета (А) и конечное (B): 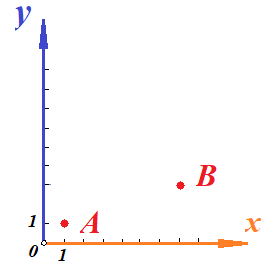 Однако, при такой аналитике возникает неопределенность – как двигался предмет между этими координатами? На этот вопрос возможно ответить множеством способов: 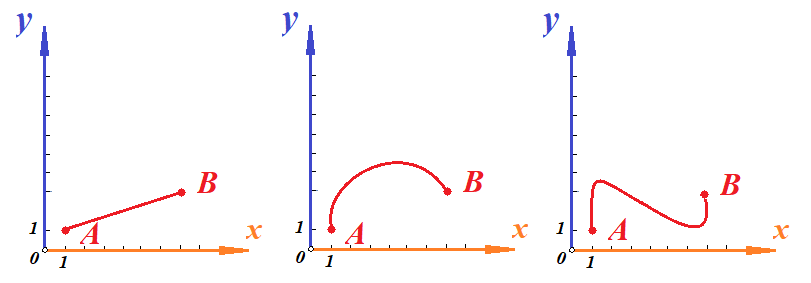 И все эти ответы – будут верными, поскольку мы не имели никакой переменной, от которой зависит координата, выбрать единственно истинный вариант не представляется возможным. Поэтому, очевидно, что для полноты описания процесса движения необходимо наблюдать за движением на протяжении всего времени движения, что неизбежно приводит к необходимости использования прибора, измеряющего время. Тогда, пользуясь понятием функции, можно утверждать: координата предмета в процессе движения зависит от момента времени наблюдения (иначе говоря – в разные моменты времени предмет оказывается в разных местоположениях [координатах]). Для лучшего понимания рассмотрим простой пример. Допустим, мы наблюдаем за некоторым предметом, движущимся вдоль прямой линии, и нами был установлен факт, что каждую секунду предмет смещается относительно прошлого положения на 1 метр. Как можно записать подобное в виде функции, если мы знаем, что каждую секунду предмет смещается на 1 метр? (для простоты, предположим, что предмет все время движется в одном и том же направлении). Получаем следующую функцию: 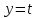 , где y-координата предмета в момент времени t. , где y-координата предмета в момент времени t.Или же, это выражение можно записать как: 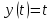 Проверим данное выражение с помощью подстановки переменной t:
Действительно, мы видим, что в каждую последующую секунду координата на единицу больше, чем в предыдущий момент времени. Изобразим полученную функцию: 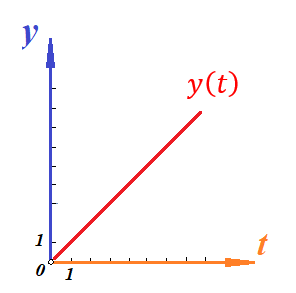 Действительно, по такой функции мы можем определить координату предмета в любой момент времени. Разобранная нами линейная зависимость – далеко не единственная. Координата предмета может зависеть о времени любым образом (параболически, гиперболически, логарифмически, синусоидально и т.д.). Мы поняли, что координату предмета можно представить в виде функции времени. Возникает новый вопрос – представим, что у нас имеется два предмета, которые меняют свою координату в процессе движения. Тогда перед нами открывается новая возможность – оценить, какой из предметов быстрее меняет свое местоположение, а именно – сравнить скорости их движения. Сделаем это графически, в начале для одного предмета: Допустим, что координата предмета зависит от времени следующим образом: 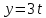 По заданному уравнению, построим график: 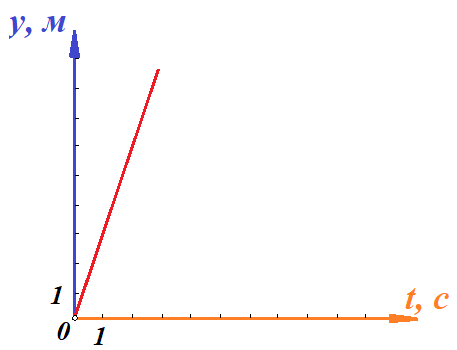 Отметим на графике функции координаты двух точек, в которых побывал предмет в процессе движения: 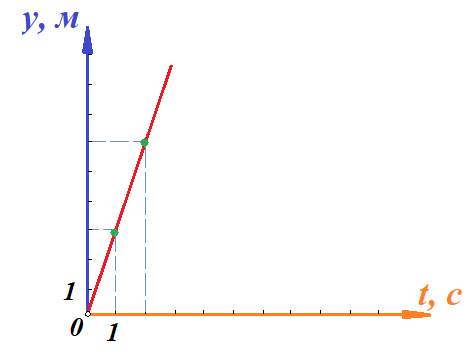 Из рисунка видно, что нами были выбраны координаты 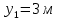 и и 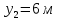 . Предмет находился в координате . Предмет находился в координате 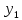 в момент времени в момент времени 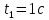 , а в координате , а в координате 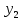 в момент времени в момент времени 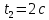 . .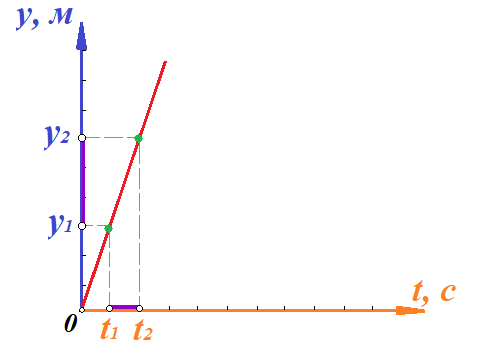 На рисунке выше видно, что мы выделили отрезки, равные разнице между координатами и разнице между моментами времени. В физике такие отрезки обозначаются как: 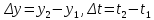 Символ 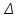 называется «дельта». Таким образом из рисунка видно, что координата называется «дельта». Таким образом из рисунка видно, что координата 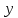 изменилась на величину изменилась на величину 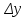 , а прошедшее время равно , а прошедшее время равно 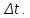 Иначе говоря: предмет переместился на расстояние Иначе говоря: предмет переместился на расстояние 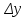 за время за время 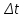 . .Обозначим данные отрезки на рисунке: 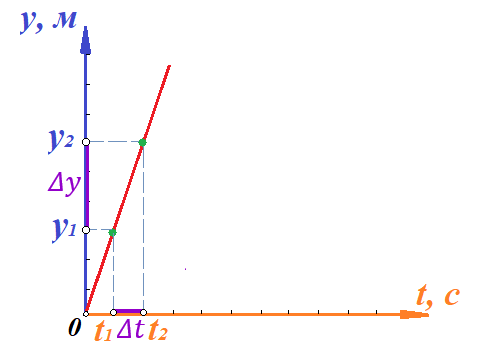 Параллельным переносом перенесем отрезок 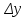 вправо, а отрезок вправо, а отрезок 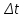 вверх: вверх: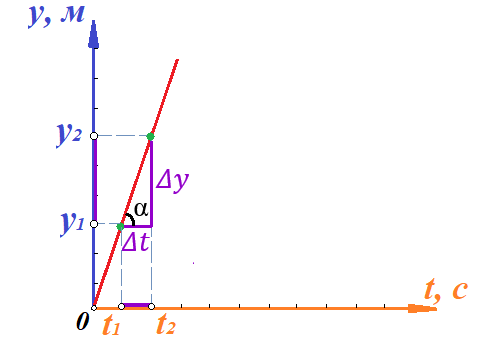 Мы видим, что образуется прямоугольный треугольник. Отметим в этом треугольнике угол α (угол между функцией [прямой красной линией] и горизонталью [осью x]). Как видно из рисунка, данный угол может быть определен, как: 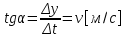 Это есть ни что иное, как скорость. Таким образом, можем сделать следующий важный вывод: если построить график функции координаты, зависящей от времени, затем отметить две произвольные координаты и соответствующие им моменты времени, то построив прямоугольный треугольник из отрезков 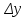 и и 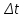 , становится возможным определить тангенс угла наклона функции, или же, говоря иначе, определить скорость. , становится возможным определить тангенс угла наклона функции, или же, говоря иначе, определить скорость.Логически очевидно, что чем больше угол наклона (больше тангенс), тем выше скорость движущегося предмета. Обратите внимание! Для линейной функции координаты угол наклона α остается постоянным! Поскольку скорость предмета численно равна углу наклона функции к горизонту, то из этого следует, что скорость предмета, координата которого зависит от времени линейно, является величиной постоянной, т.е. от времени не зависит. 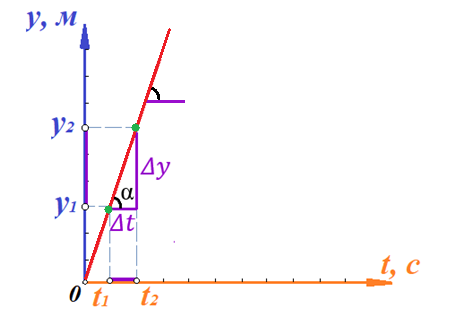 Действительно, где бы мы не провели горизонталь, угол наклона α между функцией (красной линией) и горизонталью остается один и тот же. Для еще большей наглядности приведем график функции координаты от времени, когда координата зависит от времени квадратично (параболически), т.е. согласно уравнению 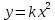 : :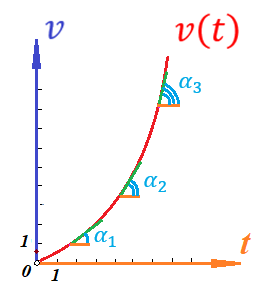 Мы сразу замечаем, что для такой зависимости скорость предмета постоянной не является, поскольку угол наклона функции (на самом деле, касательной) к горизонту – величина переменная. То есть, скорость предмета для случая, когда координата предмета зависит от времени квадратично, уже не остается постоянной, а изменяется с течением времени. Вернемся к работе с уравнениями движения предметов, координата которых зависит линейно от времени. Для наглядности приведем сравнение скорости двух предметов, координаты которых имею разные зависимости от времени 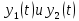 : :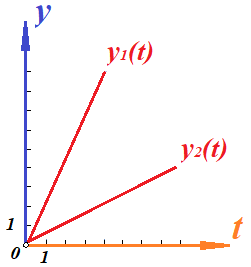 Сразу заметим, что данные функции имеют разный угол наклона 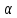 , т.е. предметы имеют различные скорости. , т.е. предметы имеют различные скорости.Повторим все действия, описанные выше, и получим следующий рисунок:  Обратите внимание! Чтобы сравнить скорость двух предметов по графику функции координаты, необходимо проводить измерения  предметов за одно и то же время предметов за одно и то же время  . .Из рисунка видно, что за одно и тоже время 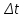 , координата предмета 1 изменилась на , координата предмета 1 изменилась на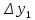 , а координата предмета 2 на , а координата предмета 2 на 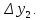 За одно и тоже время наблюдения координата предмета 1 изменяется на б За одно и тоже время наблюдения координата предмета 1 изменяется на б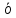 льшую величину, чем координата предмета 2. Из этого следует, что скорость предмета 1 больше, чем скорость предмета 2, поскольку: льшую величину, чем координата предмета 2. Из этого следует, что скорость предмета 1 больше, чем скорость предмета 2, поскольку: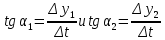 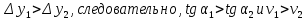 Приведем еще один пример для закрепления изученного материала. На рисунке ниже изображены три функции координат от времени (функции координат трех движущихся предметов в зависимости от времени): 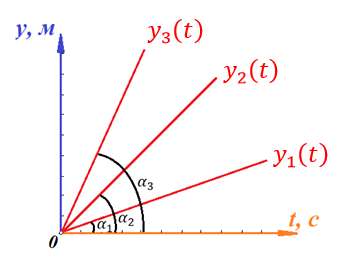 Из сказанного выше сразу становится ясно, что наибольшей скоростью обладает предмет 3 – его функция координаты имеет наибольший угол наклона α. Если это не сразу очевидно, то рекомендуется проделать те же действия, что мы проделали для сравнения скорости двух предметов (за одно и то же время 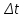 измерить измерить 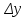 для каждой функции). для каждой функции).Выше нами было упомянуто, что скорость предмета не всегда является постоянной (изображение углов наклона функции для примера с параболической зависимостью координаты от времени). Если мы установили, что скорость – есть характеристика того, как быстро координата предмета изменяется при его движении с течением времени, то наверняка, должна существовать характеристика того, как быстро меняется скорость предмета с течением времени. Да, она существует, и называется она – ускорение. Мы руководствуемся теми же положениями – для полноты картины нам необходимо знать скорость предмета в каждый момент времени, то есть нам необходимо знать зависимость скорости от времени. Для того, чтобы получить выражение, позволяющее вычислить ускорение, рассмотрим график зависимости скорости некоторого предмета от времени (для простоты – вновь линейный). Допустим, что скорость предмета зависит от времени следующим образом: 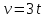 Построим график этой функции: 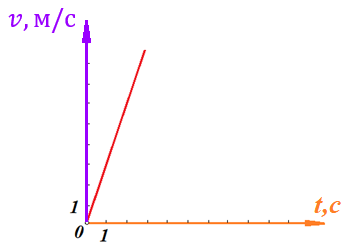 Отметим на графике функции скорости двух точек, в которых побывал предмет в процессе движения: 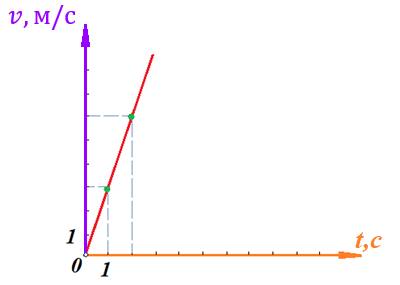 Из рисунка видно, что нами были выбраны скорости 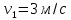 и и 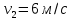 . Предмет обладал скоростью . Предмет обладал скоростью 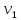 в момент времени в момент времени 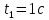 , а скоростью , а скоростью 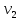 обладал в момент времени обладал в момент времени 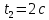 . .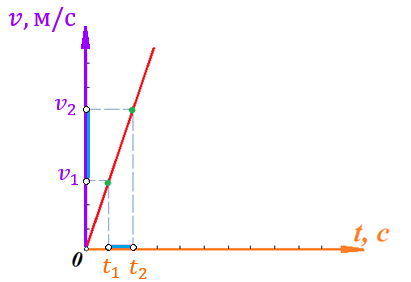 На рисунке выше видно, что мы выделили отрезки, равные разнице между скоростями предмета и разнице между моментами времени, в которых предмет обладал данными скоростями. 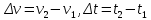 Аналогично рассмотренному выше, мы можем сказать, что за время 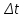 скорость предмета изменилась на величину скорость предмета изменилась на величину 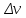 . .Обозначим данные отрезки на рисунке: 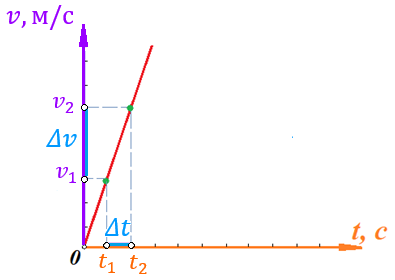 Параллельным переносом перенесем отрезок 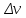 вправо, а отрезок вправо, а отрезок  вверх: вверх: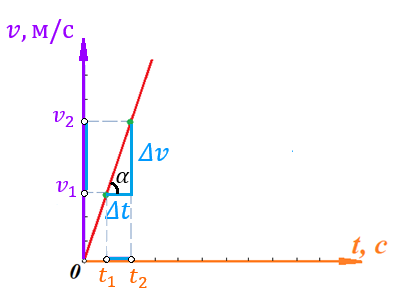 Мы видим, что образуется прямоугольный треугольник. Отметим в этом треугольнике угол α (угол между функцией [прямой красной линией] и горизонталью [осью x]). Как видно из рисунка, данный угол может быть определен, как: 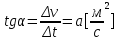 Это есть ни что иное, как ускорение. Таким образом, можем сделать следующий важный вывод: если построить график функции скорости, зависящей от времени, затем выбрать две произвольные скорости и соответствующие им моменты времени, то построив прямоугольный треугольник из отрезков |
