Теоретическая справка для кинематики ЕГЭ. Кинематика ЕГЭ. Основы кинематики
 Скачать 0.6 Mb. Скачать 0.6 Mb.
|
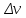 и и 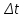 , становится возможным определить тангенс угла наклона функции, или же, говоря иначе, определить ускорение. , становится возможным определить тангенс угла наклона функции, или же, говоря иначе, определить ускорение.Говоря иначе: ускорение есть характеристика быстроты изменения скорости по величине в течении времени. Однако, необходимо остановиться на этом подробнее. Скорость – векторная величина, а как известно, люба векторная величина имеет две характеристики – величину и направление. То есть, векторная величина считается полностью заданной, если нам известна ее величина (значение) и направление (куда она направлена). В процессе движения как величина, так и направление скорости предмета могут меняться. По этой причине в кинематике вводится два ускорения – тангенциальное 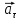 и нормальное и нормальное 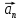 . .Формула, полученная нами выше для ускорения, определяет тангенциальное ускорение: 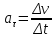 То есть тангенциальное ускорение характеризует быстроту изменения величины скорости с течением времени. Второе ускорение – нормальное. Нормальное ускорение характеризует быстроту изменения скорости по направлению с течением времени и определяется как: 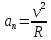 Остановимся подробнее на нормальном ускорении. Нами было сказано, что нормальное ускорение характеризует, как быстро поворачивает скорость предмета в процессе движения с течением времени. Это происходит, например, когда мотоциклист заворачивает на дороге, или, когда человек обходит какое-либо препятствие. Примеров можно привести очень много. Однако в формуле для вычисления нормального ускорения присутствует радиус – почему? Потому что любой поворот происходит по какой-либо дуге, а каждая дуга характеризуется радиусом, т.е. для каждой дуги можно достроить окружность. На рисунке ниже представлены три случая, когда предмет движется по дуге различного радиуса: 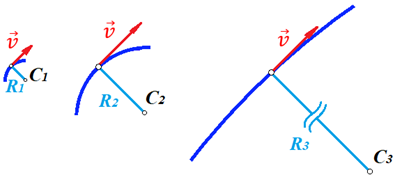 Предполагая, что скорость движения предмета во всех трех изображенных случаях одинакова, мы понимаем, что наибольшее нормальное ускорение будет на крайнем рисунке слева – там наименьший радиус кривизны дуги, по которой движется предмет. То есть, вектор скорости движущегося предмета на крайнем рисунке слева чаще всего поворачивает в этом случае. Крайний рисунок справа – там предмет движется по дуге с очень большим радиусом, то есть, вектор скорости в этом случае поворачиваться будет медленнее, чем в двух других случаях. Для лучшего понимания данных рисунков можно привести аналогию. Движение предмета на крайнем рисунке слева можно ассоциировать с движением человека вокруг небольшого магазина, а крайний рисунок справа – движение человека вдоль поверхности Земли. В первом случае человек будет часто заворачивать, то есть обладать большим нормальным ускорением, а во втором – при таком огромном радиусе траектории – мы даже не поймем, что вектор нашей скорости поворачивает, то есть будет обладать очень малым нормальным ускорением. Внесем дополнительную ясность, рассмотрев следующие возможные случаи движения предмета: 1. Предмет движется строго по прямой с постоянной по величине скоростью. В таком случае предмет не имеет ни тангенциального, ни нормального ускорений, поскольку в процессе движения не изменяется ни величина скорости, не ее направление. 2. Предмет движется строго по прямой с изменяющейся по величине скоростью. В данном случае предмет обладает тангенциальным ускорением, но не обладает нормальным, поскольку в процессе движения меняется величина скорости, но не меняется направление вектора скорости. 3. Предмет движется по дуге с постоянной по величине скоростью. В данном случае предмет не обладает тангенциальным, но обладает нормальным ускорением, поскольку в процессе движения изменяется направление вектора скорости, а величина скорости – постоянна. 4. Предмет движется по дуге с изменяющейся по величине скоростью. В данном случае предмет обладает и тангенциальным, и нормальным ускорениями, поскольку в процессе движения меняется и величина скорости, и ее направление. Обратите внимание! Речь идет именно о повороте вектора скорости в процессе движения. Если предмет двигался, предположим, слева направо, а затем повернуло и начало движение справа налево, то в данном случае нормального ускорения не будет, поскольку предмет, двигаясь в одном направлении, чтобы начать двигаться в противоположном, должно остановиться, а это считается уже за новый процесс движения. Поэтому, важно понимать, что речь идет именно о повороте вектора скорости в процессе движения, и нормальное ускорение – характеристика, как быстро происходит поворот скорости в процессе движения. Остановимся на одном важном моменте. Выше мы определили, что если скорость движущегося предмета изменяется по величине, то данный предмет обладает тангенциальным ускорением. Однако, скорость может как увеличиваться, так и уменьшаться по значению. Движение, при котором величина (модуль) скорости движущегося предмета увеличивается – называется ускоренным, а движение, при котором модуль скорости уменьшается – называется замедленным. Если же предмет движется с постоянной по модулю скоростью (модуль скорости постоянен), то такое движение называется равномерным. Однако, на этом классификация движения не исчерпывается. Тангенциальное ускорение может быть и постоянным, и переменным по величине. Приведем выше рассмотренный пример еще раз: 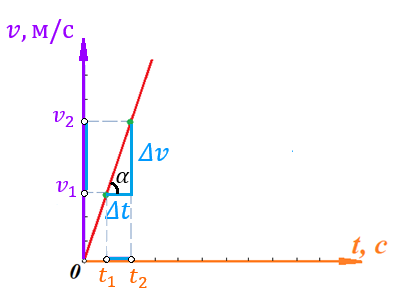 На данном рисунке нами был построен график функции скорости, зависящей от времени как 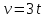 , т.е. скорость зависит от времени линейно. Как видно из рисунка, тангенциальное ускорение численно равно тангенсу угла между функцией (красная линия) и горизонталью (ось х). В данном примере угол наклона постоянен, следовательно, и тангенс этого угла постоянен, и окончательно – постоянно тангенциальное ускорение. Такое справедливо только для линейной зависимости скорости от времени. , т.е. скорость зависит от времени линейно. Как видно из рисунка, тангенциальное ускорение численно равно тангенсу угла между функцией (красная линия) и горизонталью (ось х). В данном примере угол наклона постоянен, следовательно, и тангенс этого угла постоянен, и окончательно – постоянно тангенциальное ускорение. Такое справедливо только для линейной зависимости скорости от времени. Если тангенциальное ускорение постоянно и не зависит от времени, то такое движение называется либо равноускоренным (модуль скорости увеличивается), либо равнозамедленным (модуль скорости уменьшается). Если же угол наклона функции скорости постоянно меняется, то такое движение будет просто ускоренным, или замедленным, поскольку ускорение уже не является постоянным (то есть, ускорение является постоянным только тогда, когда скорость зависит от времени линейно, т.к. только в этом случае угол наклона функции остается постоянным). Перейдем к дальнейшему изучению структуры кинематики. В процессе движения предмет движется согласно различного вида уравнениям координат. Для характеристики расстояния, пройденного предметом в процессе движения, существует несколько важных терминов. Траектория – это линия (кривая, прямая), которую описывает предмет в процессе своего движения (кривая, вдоль которой движется предмет). Траектории могут иметь бесконечно разнообразный вид, однако в заданиях ЕГЭ это либо прямая, либо парабола. 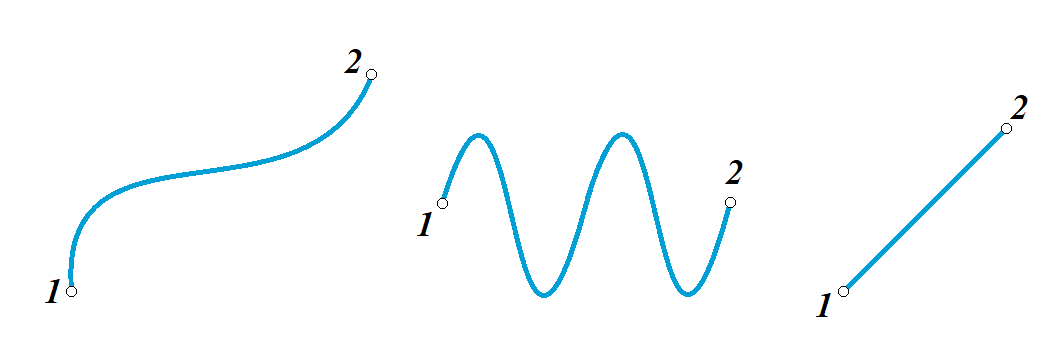 Путь, 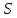 – это длина всей траектории, вдоль которой происходил процесс движения предмета. – это длина всей траектории, вдоль которой происходил процесс движения предмета.Перемещение, 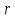 – это отрезок, равный разности между конечной и начальной координатой предмета (отрезок, проведенный из начальной координаты в конечную, модуль [значение] перемещения равно длине этого отрезка). – это отрезок, равный разности между конечной и начальной координатой предмета (отрезок, проведенный из начальной координаты в конечную, модуль [значение] перемещения равно длине этого отрезка).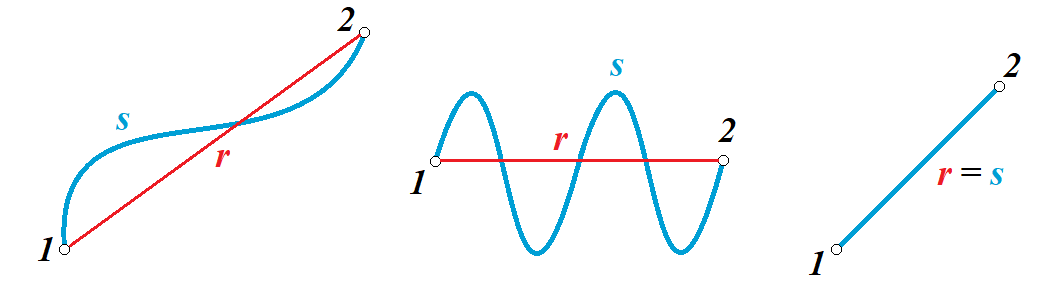 Представьте, что вы направляетесь в магазин, расположенный в 500 метрах от вас, а затем возвращаетесь обратно в исходное местоположение. Тогда ваш путь будет равен 1000 метров, а перемещение – нулю. Данный пример приведен для лучшего понимания различия в данных терминах. Благодаря выше изложенному материалу, нам стало ясно, что для однозначного определения местоположения предмета необходимо задать его координату в некоторой системе координат. Тогда мы знаем, где оно находится (необходимо иметь ноль координат, относительно которого исчисляется координата предмета). Если предмет начинает движение, то для однозначного определения траектории движения (кривой, вдоль которой движется предмет), нам необходимо для каждой координаты знать момент времени, ей соответствующий. Тогда мы сможем построить зависимость координаты от времени. Затем, по такой зависимости мы сможем определить быстроту изменения координаты с течением времени (то есть определить скорость). Если же скорость предмета меняется по величине с течением времени, то такой предмет обладает тангенциальным ускорением (в случае, если ускорение постоянно – движение может быть либо равноускоренным, либо равнозамедленным; если же тангенциальное ускорение переменное – движение будет называться ускоренным, и наконец, если скорость предмета не меняется, то такое движение называется равномерным, а тангенциальное ускорение будет равно нулю). Однако, стоит добавить, что если вектор скорости меняет направление в процессе движение, то предмет обладает также нормальным ускорением. Рассмотрим несколько примеров. Пример 1. Проанализируем уравнение координаты, зависящей от времени следующим образом: 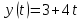 Для наглядности, построим график этой функции:
График функции координаты от времени будет иметь вид: 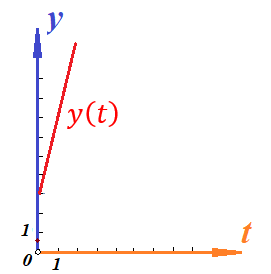 Определим величину скорости, как мы делали это выше: 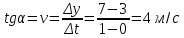 Угол наклона функции координат – постоянный, следовательно, постоянна и скорость. Тогда уравнение скорости будет иметь вид: 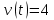 Построим график зависимости скорости от времен: 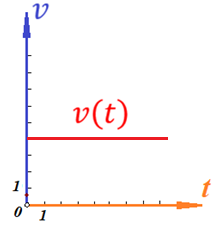 Поскольку скорость предмета не изменяется по величине, то тангенциальное ускорение равно нулю. Тогда график зависимости тангенциального ускорения от времени будет иметь вид: 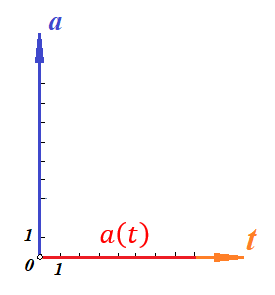 Нормальным ускорением предмет обладать не будет, поскольку движется строго по прямой. Пример 2. Проанализируем уравнение координаты предмета, зависящее от времени следующим образом: 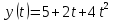 Для наглядности, построим график этой функции:
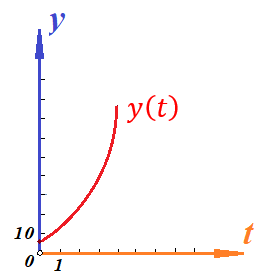 Для того, чтобы определить зависимость скорости от времени для данной зависимости координаты от времени, мы уже не можем воспользоваться определением тангенса угла наклона функции, поскольку угол все время меняется. В полноценном курсе физике в таком случае применяют производную, однако, нам изучать ее необходимости нет. Поэтому, пришло время привести уравнения, с помощью которых можно решить большинство кинематических задач. Их всего два, и применяются они только для равномерного и равноускоренного (равнозамедленного) движений! Первое уравнение есть уравнение координаты: 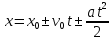 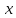 – координата предмета в момент времени – координата предмета в момент времени 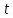 ; ;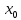 – начальная координата предмета; – начальная координата предмета;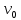 – начальная скорость предмета; – начальная скорость предмета;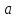 – ускорение предмета (для квадратичной зависимости координаты от времени ускорение будет постоянным [это было рассмотрено выше], а для линейной зависимости координаты от времени– то есть для равномерного движения – равно нулю). – ускорение предмета (для квадратичной зависимости координаты от времени ускорение будет постоянным [это было рассмотрено выше], а для линейной зависимости координаты от времени– то есть для равномерного движения – равно нулю).В простейшем случае – знак + соответствует равноускоренному движению, знак «-» - замедленному. Более подробно этот нюанс будет рассмотрен позже в примерах. Второе уравнение – уравнение скорости: 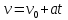 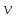 – скорость предмета в момент времени – скорость предмета в момент времени 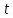 . .Возвратимся к решению задачи. С помощью полученных сведений об уравнениях кинематики, «соберем» уравнение скорости: 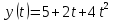 Сопоставляя данную зависимость координаты от времени, можно понять, что: 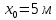 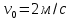 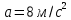 Ускорение в исходном уравнении координаты стоит с множителем ½, однако данный множитель отсутствует в заданном для анализа уравнении, следовательно, записав уравнение 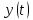 в «общем виде», получим: в «общем виде», получим: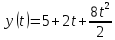 Тогда, согласно исходному уравнению скорости: 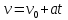 Для рассматриваемого 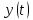 получим: получим: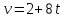 Для наглядности, построим график этой функции:
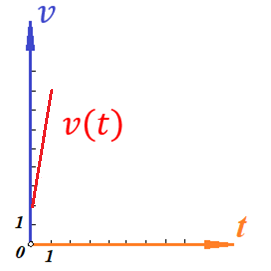 Поскольку зависимость скорости от времени – линейная, то угол наклона функции скорости всюду одинаков, т.е. ускорение предмета будет постоянным. 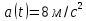 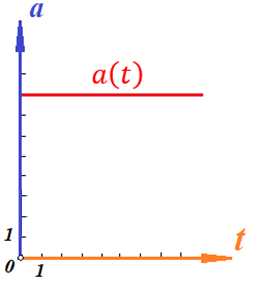 Пример 3. Дана зависимость координаты от времени 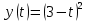 . Определить путь, перемещение, среднюю скорость пути, среднюю скорость перемещения предмета, движущегося согласно этому уравнению за время от . Определить путь, перемещение, среднюю скорость пути, среднюю скорость перемещения предмета, движущегося согласно этому уравнению за время от 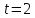 до до 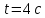 . .Для того, чтобы определить перемещение, необходимо знать, где предмет находился в начальный и конечный моменты времени. Подставим заданные моменты времени в уравнение и получим значения координат предмета: 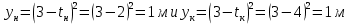 То есть, предмет вернулся в координату, с которой начал движение, из этого следует, что его перемещение равно нулю, т.е.: |