Теоретическая справка для кинематики ЕГЭ. Кинематика ЕГЭ. Основы кинематики
 Скачать 0.6 Mb. Скачать 0.6 Mb.
|
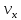 и и 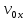 направлены вдоль положительного направления оси х, следовательно будут иметь знак «+» в уравнениях. направлены вдоль положительного направления оси х, следовательно будут иметь знак «+» в уравнениях.С учетом всего выше сказанного, имеем: 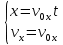 Горизонтальную координату в конце движения, как и в предыдущем примере, назовем дальностью и обозначим как 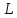 . .Заметим также, что предмет достигает дальности на протяжении всего полета, то есть справедливо дать индекс у времени движения. Окончательно получим: 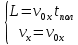 Теперь составим уравнения для оси y: 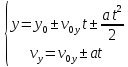 Начальная координата по оси 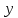 равна нулю, конечная – равна высоте подъема. Начальная скорость вдоль оси равна нулю, конечная – равна высоте подъема. Начальная скорость вдоль оси 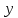 равна равна 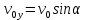 . Единственное ускорение, существующее в вертикальной плоскости – ускорение свободного падения . Единственное ускорение, существующее в вертикальной плоскости – ускорение свободного падения 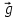 . Поскольку ось y направлена вверх, то начальная скорость . Поскольку ось y направлена вверх, то начальная скорость 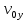 , а также скорость , а также скорость 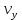 будут иметь положительные знаки, а ускорение свободного падения направлено вниз, следовательно, будет записано со знаком минус. будут иметь положительные знаки, а ускорение свободного падения направлено вниз, следовательно, будет записано со знаком минус. Получим предварительно: 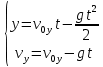 Обратим внимание, что максимальная высота подъема достигается в верхней точке траектории. В этой точке вертикальная скорость обращается в ноль, то есть дальнейший подъем вверх прекращается. Следовательно, 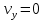 . .Заметим, что время подъема предмета до максимальной высоты в два раза меньше времени полета (времени, на котором достигается дальность полета). Тогда, с учетом всего вышесказанного, получим: 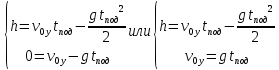 Таким образом, исходная система уравнений кинематики для броска под углом к горизонту имеет следующий вид: 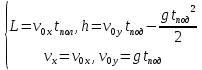 Поставим себе задачу – получить формулы для высоты и дальности, в которых будут присутствовать только начальная скорость и угол, под которым совершен бросок. Приступим: Из уравнения скорости для оси y определим время подъема: 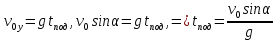 Очевидно, что время полета: 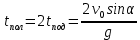 Теперь можем определить дальность полета: 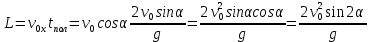 Определим максимальную высоту подъема предмета в процессе движения: 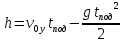 Подставим в это уравнение ранее найденное 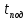 : :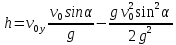 Где 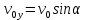 , тогда: , тогда: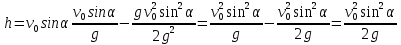 Таким образом, нами были получены важные формулы: 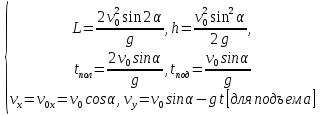 Пример 10. Два предмета, находящиеся на одной вертикали, начинают движение. Один предмет брошен вертикально вверх с начальной скоростью 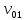 , второй начинает вертикальное падение вниз с начальной скоростью , второй начинает вертикальное падение вниз с начальной скоростью 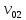 . Изначально, расстояние между предметами было равно . Изначально, расстояние между предметами было равно 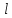 . Определить момент времени, когда предметы встретятся. . Определить момент времени, когда предметы встретятся.В данной задаче мы уже имеем дело с движением сразу двух предметов одновременно. Причем, эти предметы движутся навстречу друг другу. Для начала, сделаем рисунок: 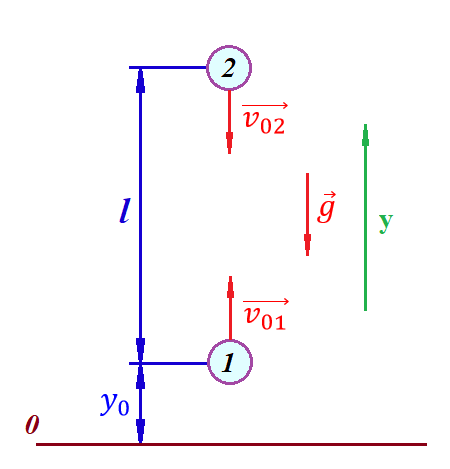 Важный момент! Если мы решаем задачу с двумя предметами, то расстановка знаков у скоростей и ускорений происходит относительно одной и той же оси! Как видно из рисунка, положительное направление оси 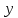 направлено вверх. направлено вверх.Запишем уравнение координаты для первого предмета: 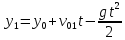 Запишем уравнение координаты для второго предмета: 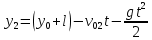 Обратите внимание на знаки у множителей начальных скоростей и ускорений свободны падений у обоих предметов. Поскольку нас интересует место их встречи, то: 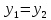 Тогда: 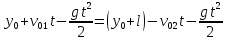 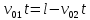 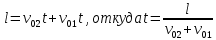 Мы определили время, соответствующее моменту встречи предметов. Примечание: если бы в задаче был поставлен вопрос об определении координаты, в которой предметы встретятся, то 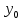 можно было бы принять равным нулю, поскольку никакой информации о том, откуда отсчитываются координаты – нет. Именно для этого в решении задачи взята некоторая начальная координата можно было бы принять равным нулю, поскольку никакой информации о том, откуда отсчитываются координаты – нет. Именно для этого в решении задачи взята некоторая начальная координата  (которая, как видно, сокращается и на результат времени встречи не влияет). (которая, как видно, сокращается и на результат времени встречи не влияет).Приведем альтернативное решение, в котором ось  будет направлена вниз: будет направлена вниз: Очевидно, что теперь ноль координат находится сверху. Тогда уравнения координат предметов будут иметь вид: 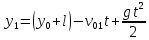 Для второго предмета: 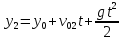 Далее: 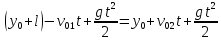 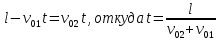 В очередной раз мы показали, что направление оси не влияет на результат, поскольку симметрично «отзеркаливает» направления всех векторов. Далее, изучим еще один класс задач, предварительно дав несколько определений. В кинематике существуют задачи, в которых ставится целью определить относительную скорость. Относительная скорость – это скорость одного предмета относительно второго, в предположении, что один из этих предметов – покоится. Поясним на примере. Предположим, что предмет 1 движется направо со скоростью 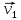 , а предмет 2 движется налево со скоростью , а предмет 2 движется налево со скоростью 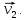 Сделаем рисунок: Сделаем рисунок: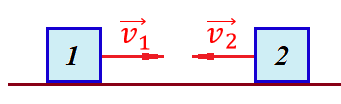 Если поставить задачу вычислить относительную скорость, то необходимо представить, как один из предметов покоится (например, предмет 1). Тогда предмет 2 движется со скоростью: 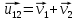 Относительно покоящегося предмета 1. Изобразим это: 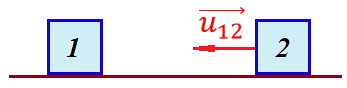 Рассмотренный пример можно привести в ином виде – представить себе два автомобиля, движущихся навстречу друг другу с некоторыми скоростями, тогда скорость их относительного сближения равна сумме скоростей автомобилей. Если бы предметы 1 и 2 двигались бы в одном направлении (друг за другом), то относительная скорость вычислялась бы как: 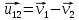 Если бы оба предмета двигались в противоположенные стороны, то их скорость «разбегания» вычислялась бы как: 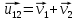 Пример 11. Человек идет с собственной скоростью 5 м/с по вагону. С какой скоростью движется человек относительно вагона, если скорость последнего 40 м/с? С какой скоростью человек движется относительно Земли? Поскольку вагон покоится относительно человека, то его скорость относительно вагона равна 5 м/с. Относительно Земли скорость человека будет равна 45 м/с. Рассмотрение относительной скорости было неслучайным. Пришло время определить рассматриваемые нами системы отсчета (системы координат, в которых помимо местоположений предметов нам известно течение времени, то есть мы обладаем измерителем времени). В нашем курсе мы будем работать только в инерциальных системах отсчета. Инерциальные системы отсчета – это такие системы отсчета, которые покоятся, или же движутся с постоянной скоростью. Более подробно этот вопрос будет раскрыт в разделе динамика. Однако, рассмотренный выше пример с вагоном, демонстративен. Система отсчет вагона, движущегося с постоянной скоростью, для предмета является инерциальной. Система отсчета Земли, покоящейся относительно человека, также является инерциальной. Система отсчета перестает быть инерциальной, когда она начинает двигаться с ускорением. И тогда она называется неинерциальной. Однако, как сказано выше, этот вопрос будет поднят подробно в будущем. Следующим разделом кинематики, который мы рассмотрим, будет вращательное движение – движение, при котором предмет движется вокруг некоторой оси или точки. Да, выше мы рассматривали линейное, или, как его еще называют – поступательное движение (это движение, при котором предмет движется вдоль прямой). Да, частично мы касались движения по окружности, и ввели понятие нормального ускорения, однако нормальное ускорение – линейная характеристика, поскольку является мерой того, как часто поворачивает вектор линейной скорости  . .Теперь пришло ввести понятия угловых величин – величин кинематики, используемых при вращательном движении. В поступательном движении мы характеризовали положение предмета с помощью координаты. Однако, в ряде задач на вращательное движение оказывается удобным ввести понятие угла поворота 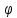 . .Угол поворота – величина, характеризующая положение предмета, движущегося по окружности (то есть, показатель того, на какой угол повернулся предмет относительно некоторого начального значения). Сделаем рисунок: 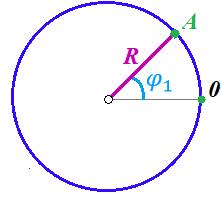 На рисунке представлен предмет А, который может двигаться по окружности радиусом 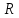 . Изначально, предмет расположен в точке, повернутой на угол . Изначально, предмет расположен в точке, повернутой на угол 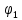 относительно горизонтального выбранного нуля. Предположим, что предмет переместился по окружности и стал повернут на угол относительно горизонтального выбранного нуля. Предположим, что предмет переместился по окружности и стал повернут на угол 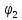 . Сделаем рисунок: . Сделаем рисунок: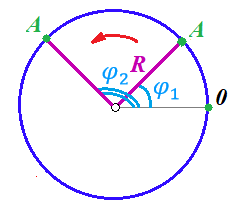 Мы видим, таким образом, что предмет A повернулся на угол: 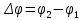 Обратите внимание! Для задания угла поворота не нужен никакой нулевой угол, поскольку он полностью определяется углом между начальным и конечным положениями предмета на окружности: 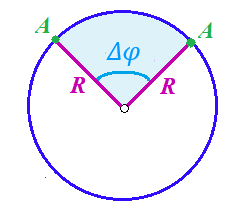 В этом и состоит удобство использования вращательных величин. Система координат, в которой положение предмета относительно центра окружности характеризуется только расстоянием от центра окружности до любой из ее точек (радиусом R) и углом поворота (φ) называется плоской круговой системой координат (на самом деле, пользуются сферической системой координат, в которой присутствует еще один угол пространственного положения, поскольку сфера – объемное тело, но в нашем курсе такое рассматриваться не может). Сделаем промежуточный вывод: при вращательном движении аналогом координаты предмета (как в поступательном движении) является угол поворота φ. Угол поворота измеряется либо в градусах (как у гражданских), либо в радианах [рад]. Приведем рисунок: 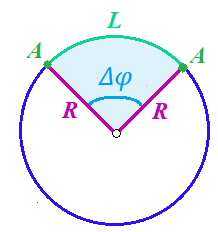 Угол поворота определяется следующим фундаментальным геометрическим равенством: 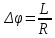 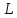 – длина сектора дуги. – длина сектора дуги.Вполне естественно, что угол поворота при движении различных предметов может изменяться с разной быстротой. В поступательном движении характеристикой быстроты изменения координаты предмета с течением времени является скорость 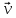 . Во вращательном движении аналогичным параметром является угловая скорость – величина, характеризующая быстроту изменения угла поворота предмета с течением времени. . Во вращательном движении аналогичным параметром является угловая скорость – величина, характеризующая быстроту изменения угла поворота предмета с течением времени.В определении направления угловой скорости есть нечто непохожее на определение направления линейной скорости предмета (в поступательном движении все очевидно – вектор скорости направлен туда, куда движется предмет). Простота вращательного движения состоит в том, что возможно всего лишь два направления вращения – либо по часовой стрелки, либо против часовой. Приведем рисунок: 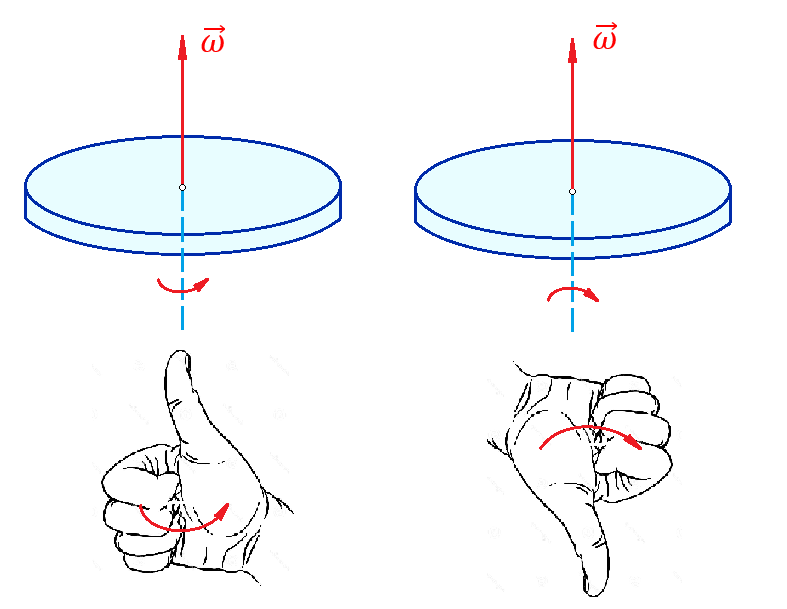 На рисунке выше изображены два вращающихся диска. Левый диск вращается против часовой стрелки, а правый – по часовой. Направление вращения – это не то же самое, что и направление угловой скорости. Для определения направления угловой скорости используют правило правой руки: 4 пальца правой руки направляем по вращению диска, тогда большой палец покажет направление угловой скорости. Рекомендуется проделать определение направления самостоятельно. Если бы мы смотрели на вращающийся диск сверху, то картина имела бы следующий вид: 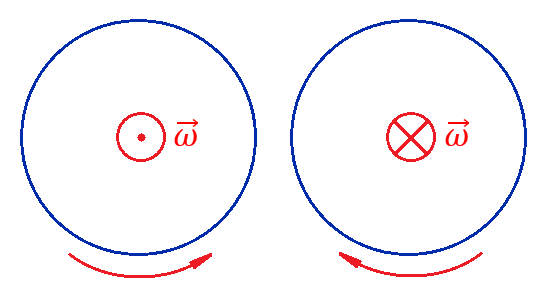 Направление «на нас» отмечается кружком с точкой, направление «от нас» отмечается кружком с крестиком. Вернемся к раскрытию понятия угловая скорость. Согласно выше сказанному, угловая скорость может быть вычислена следующим образом: 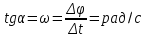 Формула получена аналогично формуле, рассмотренной выше (мы рассматривали линейную зависимость координаты предмета от времени, выбрали два момента времени и соответствующие этим моментам времени координаты, отметили угол α – угол наклон функции к горизонту и затем записали выражение для тангенса этого угла наклона, который и оказался равным скорости). Из этого следует, что угловая скорость есть тангенс угла наклона функции угла поворота, зависящего от времени. Как и ранее, если дана линейная зависимость угла поворота от времени, то угловая скорость будет постоянной (так как угол наклона не меняется). Угловая скорость, как и линейная, является векторной величиной. Однако, мы не будем касаться случаев, когда предмет может менять направление вращения, поскольку это выходит далеко за рамки курса. В кинематике поступательного движения параметром, характеризующем быстроту изменения скорости по величине было тангенциальное ускорение. В кинематике вращательного движения параметром, характеризующим быстроту изменения величины угловой скорости, является угловое ускорение: 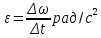 То есть, угловое ускорение есть тангенс угла наклона функции угловой скорости, зависящей от времени. Разумеется, постоянным угловое ускорение будет только тогда, когда зависимость угловой скорости от времени линейная. Очевидно, что если вектор угловой скорости и углового ускорения имеют одно направление, то движение будет ускоренным, иначе – замедленным (добавим: если угловое ускорение постоянно по величине и направлению, то движение будет либо равнозамедленным, либо равноускоренным). Напоследок, запишем уравнения кинематики вращательного движения, подходящие для равномерного или равноускоренное движений: |
