Теоретическая справка для кинематики ЕГЭ. Кинематика ЕГЭ. Основы кинематики
 Скачать 0.6 Mb. Скачать 0.6 Mb.
|
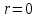 Таким образом, мы понимаем, что предмет в процессе движения останавливается в некоторой координате и затем поворачивает назад. Как найти момент времени, когда предмет поворачивает? Для этого необходимо получить уравнение скорости и приравнять его к нулю, поскольку именно в точке поворота скорость предмета обращается в ноль, а затем меняет свое направление. Имеем: 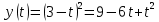 Тогда получим: 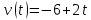 В точке поворота: 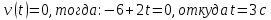 То есть, предмет поворачивает в третью секунду своего движения. Теперь определим путь. Для этого необходимо знать, в какой координате находился предмет в момент времени 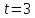 с. Имеем: с. Имеем: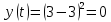 То есть, координаты предмета и соответствующие этим координатам моменты времени есть: 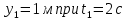 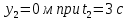 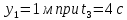 Очевидно, что путь равен 2 м. Теперь приступим к определению средней путевой и средней скорости перемещения. По определению, средней скоростью называется весь путь, пройденный предметом, деленный на время, за который этот путь был пройден: 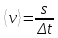 Тогда средняя путевая скорость: 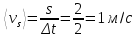 Поскольку предмет двигался 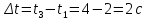 А средняя скорость перемещения: 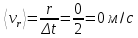 Пример 4. Рассмотрим еще одну задачу на определение перемещения и пути предмета за определенное время движения. Дана зависимость координаты от времени: 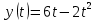 . Задача стоит та же – определить перемещение и путь предмета с момента времени . Задача стоит та же – определить перемещение и путь предмета с момента времени 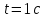 до до 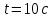 . .Мы видим, что координата зависит от времени квадратично, следовательно, движение либо равноускоренное, либо равнозамедленное. Определим, какое именно, но для начала запишем уравнение скорости. Запишем уравнение скорости этого предмета, предварительно определив: 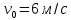 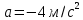 Тогда уравнение скорости будет иметь вид: 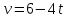 Подставляя сюда различные t, мы замечаем, что скорость с начала движения (с момента t=0) начинается уменьшаться по величине: 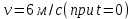 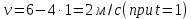 Это продолжается до определенного момента. Определим, до какого, то есть, найдем точку поворота: 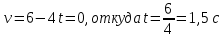 То есть, в момент времени 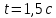 предмет останавливается, а затем начинает движение в противоположную сторону относительно начального направления движения. Действительно, скорость предмета изменит знак сразу после полуторной секунды, для наглядности подставим в уравнение скорости предмет останавливается, а затем начинает движение в противоположную сторону относительно начального направления движения. Действительно, скорость предмета изменит знак сразу после полуторной секунды, для наглядности подставим в уравнение скорости 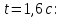 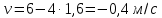 И для любого последующего момента времени величина (модуль) скорости будет увеличиваться, т.е. после 1.5 секунды предмет станет двигаться равноускоренно. Таким образом: с начала движения (t=0) до момента времени t=1,5 с предмет движется равнозамедленно, а затем, начиная с 1,5 с и до бесконечности – равноускоренно. Для того, чтобы определить путь, необходимо знать координаты предметы в три момента времени: для t=1, 1,5 и 10 секунд. 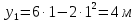 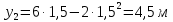 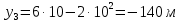 Определим путь, пройденный предметом с 1 до 10 ой секунды: С 1ой до 1.5 секунды предмет прошел путь: 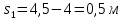 С 1,5ой до 10ой секунды предмет прошел путь: 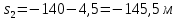 Путь – это длина траектории, то есть имеет смысл только его модуль. Таким образом, полный путь пройденный предметом с 1 до 10ой секунды: 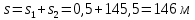 Перемещение – отрезок, соединяющий конечное положение предмета и начальное (на самом деле, говоря точно, перемещение – вектор, соединяющий конечную координату с начальной, т.е. знак у перемещения определяет направление движения предмета между начальной и конечной координатами). Определим перемещение: 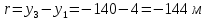 Сравним полученные результаты. Из них видно, что перемещение меньше пути на величину 1,5 метра – действительно, предмет в начале движения (до полуторной секунды) прошел в одну сторону 1,5 метра, а затем начал движение в противоположную сторону от исходного направления. Перейдем к следующему виду задач, называемых типовыми задачами ЕГЭ. К ним относится вертикальное падение предмета вниз, вертикальное бросание предмета вверх, горизонтальный бросок, бросок под углом к горизонту. Именно на типовых задачах студент способен закрепить навык применения двух основных уравнений кинематики для равноускоренного и равномерного движения. Пример 5. Вертикальное падение предмета вниз с некоторой высоты h из состояния покоя. В данной задаче предмет движется в вертикальной плоскости Земли. На Земле всюду существует ускорение свободного падения, направленное вниз (существует оно из-за силы тяжести, силы, с которой Земля притягивает предметы, находящиеся на малой высоте от поверхности Земли). Если бы в задаче присутствовали еще другие силы, то они бы тоже создавали какое-либо ускорение. Однако, для начала рассмотрим случай, когда предмет находится в состоянии покоя на некоторой высоте h над поверхностью Земли и что в процессе его движения на него действует только сила тяжести, сообщающая ему ускорение свободного падения, направленного вниз. Предмет движется из состояния покоя – означает, что в начале телу не была придана какая-либо начальная скорость, к примеру, камень, находящийся в сжатой ладони, начинает падать вниз с нулевой начальной скоростью (начинает падать, как только ладонь разжимают). Такое падение называется свободным падением. Сделаем рисунок: 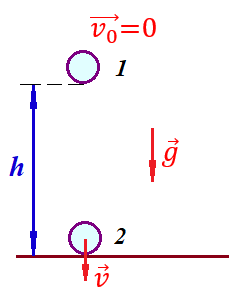 Из рисунка становится еще очевиднее, что начальное положение предмета расположено на высоте h над поверхностью Земли, конечное – на поверхности Земли. Запишем уравнения кинематики: 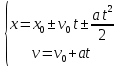 И преобразуем их для данной задачи. Во-первых, разберемся с начальной координатой. Мы заранее знаем, что предмет пролетит высоту 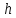 , следовательно, если мы запишем первое уравнение в таком виде: , следовательно, если мы запишем первое уравнение в таком виде: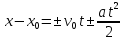 То в нем можно будет заменить разность координат высотой 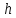 . .Тогда получим: 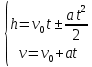 Предмет начинает свое движение из состояния покоя, т.е. 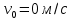 . . Тогда: 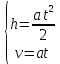 Вспомним, что единственное ускорение в этой задаче – ускорение свободного падения. Тогда: 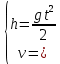 С помощью этих двух уравнений можно решить любую задачу на свободное падение, начавшееся из состояния покоя (и при условии, что в рассматриваемой задаче отсутствуют силы, кроме силы тяжести). Следует отметить, что данное движение является равноускоренным (ускорение свободного падения постоянно по величине и направлению). Приведем немного альтернативный подход. Поскольку в рассматриваемой задаче присутствуют векторные величины, то нам необходимо задать положительное направление некоторой оси, вдоль которой происходит движение (напомним, что вектор задан полностью только тогда, когда известны его величина и направление). 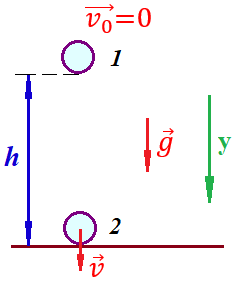 Мы выбрали положительное направление оси y вниз. Тогда вектора, направленные туда же, куда и положительное направление данной оси, будут положительными, иначе – отрицательными. Имеем: 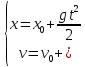 Конечная скорость и ускорение свободного падения направлены вниз, следовательно, все два данных вектора – положительные. Дальнейшие преобразования аналогичны преобразованиям выше. Пример 6. Вертикальное падение предмета вниз с некоторой высоты h с начально переданной ему скоростью. Текущая задача отличается от предыдущей только тем, что предмету придают начальную скорость, направленную вниз (в отличия от случая, когда камень начал свободное падение из разжатой ладони, в данной случае мы кидаем его вертикально вниз с некоторым «усилием», сообщающее ему начальную скорость). 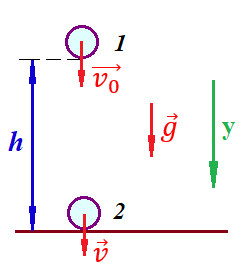 Тогда уравнения кинематики для данной задачи примет вид: 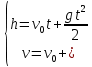 Обратите внимание – все вектора – положительные, поскольку начальная и конечная скорости, а также ускорение свободного падения – направлены вниз, то есть со направлены с положительным направлением выбранной оси. Пример 7. Вертикальное подбрасывание предмета вверх с начальной скоростью 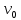 . .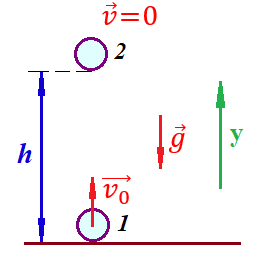 Очевидно, что начальное положение предмета находится на поверхности Земли, конечное – на некоторой высоте h. Выберем направление оси – вверх, тогда: 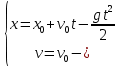 Когда предмет в процессе вертикального полета вверх достигнет точки максимального подъема, то он остановится, следовательно, конечная скорость на максимально достигнутой высоте равна нулю, тогда: 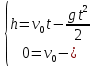 Окончательно получим: 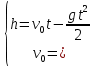 Обратите внимание – данное движение – равнозамедленное. Пример 8. Горизонтальный бросок предмета с начальной скоростью 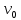 с некоторой высоты h над поверхностью Земли. с некоторой высоты h над поверхностью Земли.Данная задача отличается от рассмотренных выше тем, что предмет, брошенный горизонтально, движется сразу по двумя осям, вдоль x и вдоль y, или иначе говоря – движется в плоскости xy. Сделаем рисунок прямоугольной системы координат и изобразим на ней траекторию движения предмета: 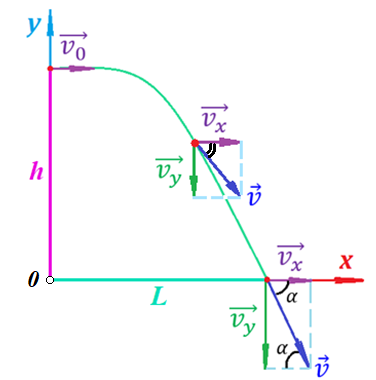 На данном рисунке изображена именно траектория (кривая, вдоль которой движется предмет), а не зависимость вертикальной координаты 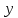 от горизонтальной от горизонтальной 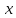 ! !Разберемся с каждой осью по очереди. Начнем с оси x. Начальное положение предмета выберем на высоте h, конечную – на некотором расстоянии 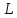 от места бросания. от места бросания.Для оси 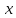 уравнения кинематики будут иметь вид: уравнения кинематики будут иметь вид: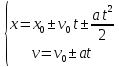 Ускорения в плоскости 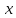 нет (не действует никаких сил). Начальная координата по оси нет (не действует никаких сил). Начальная координата по оси 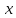 – равна нулю. Однако, если мы перенесем – равна нулю. Однако, если мы перенесем 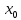 влево, то получим расстояние, на которое удалится предмет, брошенный горизонтально, т.е.: влево, то получим расстояние, на которое удалится предмет, брошенный горизонтально, т.е.: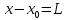 Это называется дальностью полета. Получим систему уравнений для оси 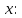 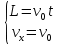 Таким образом, движение вдоль оси x – равномерное. Рассмотрим теперь ось y. 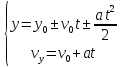 Единственное ускорение в этой задаче – ускорение свободного падения, направленное вниз. Начальной скоростью в вертикальной плоскости предмет не обладает, поскольку бросок – горизонтальный. Тогда, согласно выбранному направлению оси y, ускорение свободного падения и конечная скорость будут иметь знак «-». Получим, с учетом всего сказанного выше: 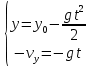 Начальная координата предмета по оси y равна 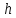 , а конечная – 0. Тогда, очевидно: , а конечная – 0. Тогда, очевидно: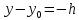 А система уравнений примет вид: 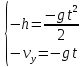 Или же: 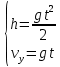 Примечание: Если бы мы направили ось y вниз, то направление ускорения свободного падения и конечная скорость имели бы положительный знак, тогда: 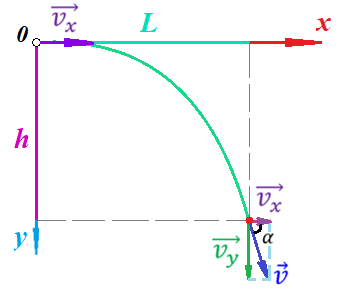 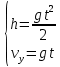 Обратите внимание, что во втором варианте вывода выражение: 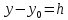 Поскольку начальная координата предмета при таком расположении осей равна нулю, а конечная – высоте 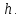 Также заметим, что вертикальная и горизонтальная скорости направлены во взаимно перпендикулярных плоскостях. Из рисунка видно, что их векторная сумма дает некоторую скорость 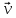 . Это скорость и есть та самая скорость, с которой предмет движется по траектории. Полная скорость вычисляется как: . Это скорость и есть та самая скорость, с которой предмет движется по траектории. Полная скорость вычисляется как: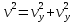 Для горизонтального бросания в качестве итога можно привести следующие формулы: 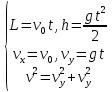 Пример 9. Бросок предмета с поверхности Земли с начальной скоростью 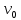 , направленной под углом α к горизонту. , направленной под углом α к горизонту.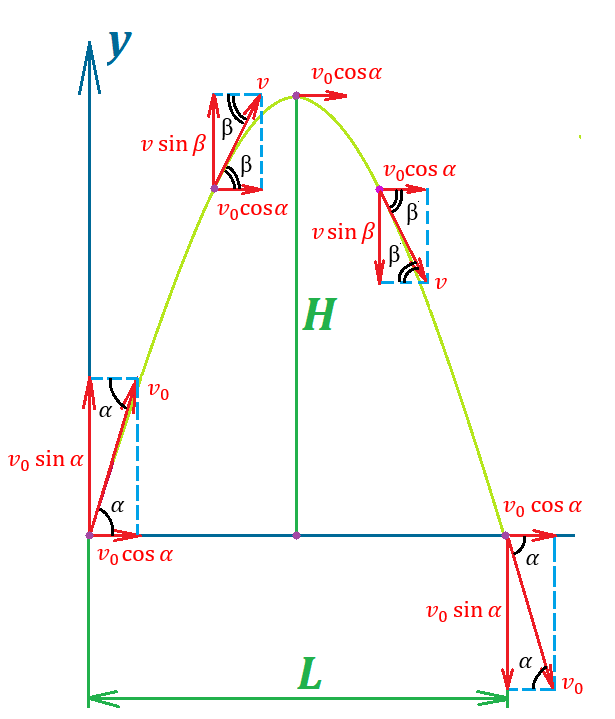 В данной задаче начальная скорость направлена ни вдоль оси х, ни вдоль оси y. Тогда для того, чтобы записать уравнения кинематики по осям координат, необходимо сделать проекции начальной скорости на ось х и ось y. Из рисунка видно, что: 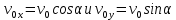 Запишем уравнения кинематики для оси х: 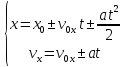 Изначально предмет находится в начале координат, следовательно, 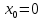 . .Начальная скорость вдоль оси x имеет величину 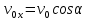 . .Вдоль горизонтальной оси никакие силы не действуют, следовательно, ускорение равно нулю. Вектора |
