ОСНОВЫ МАТЕМАТ МОДЕЛ. Основы математического моделирования социально экономических процессов
 Скачать 1.42 Mb. Скачать 1.42 Mb.
|
ВЫПОЛНЕНИЕ ПРАКТИЧЕСКИХ ЗАДАНИЙ ПО ДИСЦИПЛИНЕ ОСНОВЫ МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ СОЦИАЛЬНО - ЭКОНОМИЧЕСКИХ ПРОЦЕССОВ Группа Ом20Гу111 Студент А.Н.Руденко МОСКВА 2023 Практическая работа № 1 Регрессионный и корреляционный анализ Заполним исходные данные задачи в табл.1. После вычисления коэффициентов уравнения для различных видов зависимости (линейной, степенной, экспоненциальной), занесем полученные значения в табл. 3. Далее составим уравнения линейной, степенной, экспоненциальной регрессии и найдем значения моделей Yi для каждого Xi(значения занесем в табл. 1) 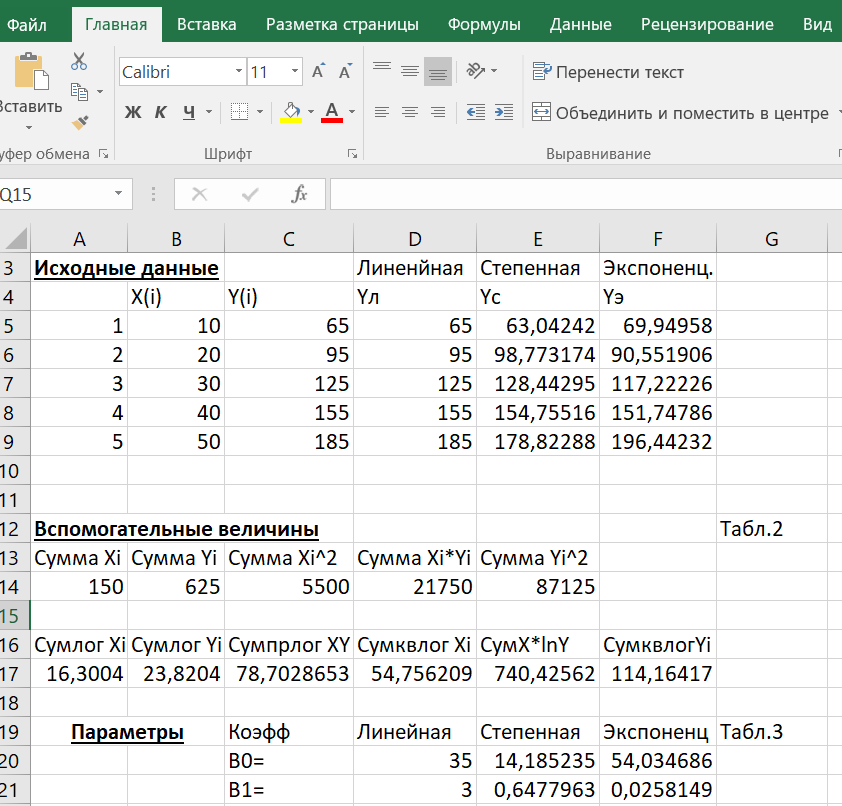 Уравнение линейной регрессии имеет вид: y=3x+35 Уравнение экспоненциальной регрессии имеет вид: y=54,034e0,02581x Уравнение степенной регрессии имеет вид : y=14,1852x0,647 Построим графики функций регрессий:  Подсчитаем коэффициент парной корреляции для линейной модели и индекс корреляции для нелинейных моделей. 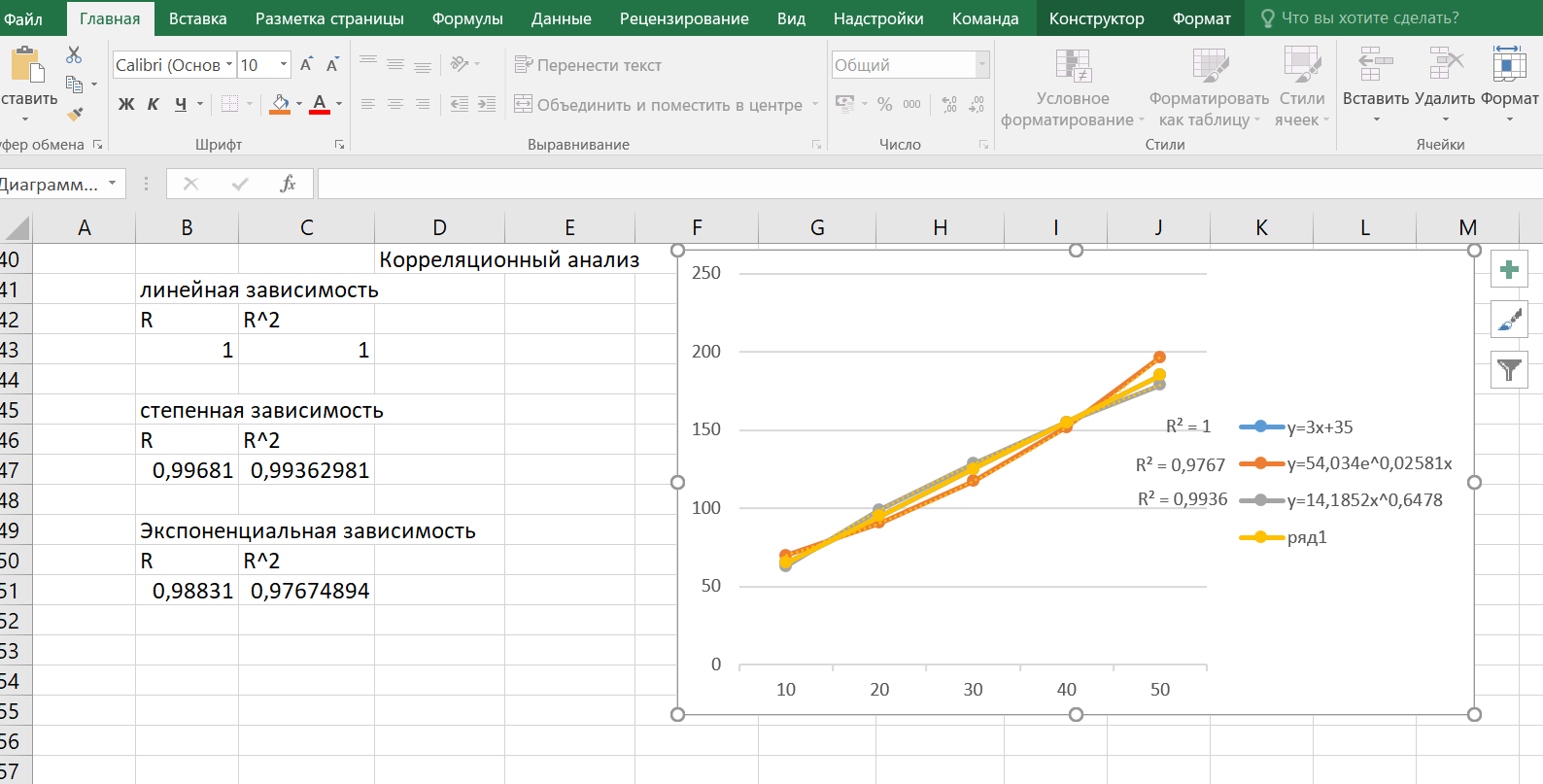 Для линейной модели коэффициенты корреляции R2, вычисленный вручную и полученный через встроенные средства программного обеспечения EXCEL, совпадают: R2р= R2=1; модуль R равен 1, связь линейна Для cтепенной модели коэффициенты корреляции R2, вычисленный вручную R2р= и полученный через встроенные средства программного обеспечения EXCEL, совпадают: R2р= R2=0,9936; т.е. разброс теоретических «ŷ» и экспериментальных «y» значений результирующей переменной относительно общего среднего значения небольшой. Модель достаточно точно описывает исходную функцию. Для экспоненциальной модели коэффициенты корреляции R2, вычисленный вручную R2р= и полученный через встроенные средства программного обеспечения EXCEL, совпадают: R2р= R2=0,9767; т.е. разброс теоретических «ŷ» и экспериментальных «y» значений результирующей переменной относительно общего среднего значения небольшой. Модель достаточно точно описывает исходную функцию. Вопросы для проверки: 1. Запишите вид парной линейной регрессии. Дайте определение всем входящим в нее элементам. Парная линейная регрессия имеет вид: 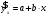 или или 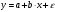 Уравнение вида 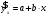 позволяет по заданным значениям фактора x (регрессора) находить теоретические значения результативного признака, подставляя в него фактические значения фактора x. Параметр b называется коэффициентом регрессии. Его величина показывает среднее изменение результата с изменением фактора на одну единицу. Параметр a, при котором нет факторов, называют часто константой. Формально — это значение функции при нулевом значении всех факторов. позволяет по заданным значениям фактора x (регрессора) находить теоретические значения результативного признака, подставляя в него фактические значения фактора x. Параметр b называется коэффициентом регрессии. Его величина показывает среднее изменение результата с изменением фактора на одну единицу. Параметр a, при котором нет факторов, называют часто константой. Формально — это значение функции при нулевом значении всех факторов.  - случайная ошибка модели. - случайная ошибка модели.2. В чем суть метода наименьших квадратов? Метод наименьших квадратов - математический метод, применяемый для решения различных задач, основанный на минимизации суммы квадратов отклонений некоторых функций от искомых переменных. Он может использоваться для «решения» переопределенных систем уравнений (когда количество уравнений превышает количество неизвестных), для поиска решения в случае обычных (не переопределенных) нелинейных систем уравнений, для аппроксимации точечных значений некоторой функции. Суть метода. Пусть x{\displaystyle x} - набор {\displaystyle n}n неизвестных переменных (параметров){\displaystyle f_{i}(x)}bbb {\displaystyle m>n} 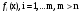 - совокупность функций от этого набора переменных. Задача заключается в подборе таких значений {\displaystyle x}x, чтобы значения этих функций были максимально близки к некоторым значениям {\displaystyle y_{i}} - совокупность функций от этого набора переменных. Задача заключается в подборе таких значений {\displaystyle x}x, чтобы значения этих функций были максимально близки к некоторым значениям {\displaystyle y_{i}} 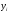 . По существу речь идет о «решении» переопределенной системы уравнений {\displaystyle f_{i}(x)=y_{i}} . По существу речь идет о «решении» переопределенной системы уравнений {\displaystyle f_{i}(x)=y_{i}}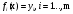 {\displaystyle i=1,\ldots ,m} в указанном смысле максимальной близости левой и правой частей системы. Суть МНК заключается в выборе в качестве «меры близости» суммы квадратов отклонений левых и правых частей {\displaystyle |f_{i}(x)-y_{i}|} {\displaystyle i=1,\ldots ,m} в указанном смысле максимальной близости левой и правой частей системы. Суть МНК заключается в выборе в качестве «меры близости» суммы квадратов отклонений левых и правых частей {\displaystyle |f_{i}(x)-y_{i}|} 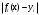 . Таким образом, сущность МНК может быть выражена следующим образом: . Таким образом, сущность МНК может быть выражена следующим образом: 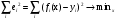 {\displaystyle \sum _{i}e_{i}^{2}=\sum _{i}(y_{i}-f_{i}(x))^{2}\rightarrow \min _{x}} {\displaystyle \sum _{i}e_{i}^{2}=\sum _{i}(y_{i}-f_{i}(x))^{2}\rightarrow \min _{x}}В случае, если система уравнений имеет решение, то наименьшее значение суммы квадратов будет равно нулю и могут быть найдены точные решения системы уравнений аналитически или, например, различными численными методами оптимизации. Если система переопределена, то есть, говоря нестрого, количество независимых уравнений больше количества искомых переменных, то система не имеет точного решения и метод наименьших квадратов позволяет найти некоторый «оптимальный» вектор{\displaystyle x}x в смысле максимальной близости векторов y{\displaystyle y} и f(x) {\displaystyle f(x)} или максимальной близости вектора отклонений {\displaystyle e}e к нулю (близость понимается в смысле евклидова расстояния). 3. Дайте интерпретацию параметров b1 и b0 линейной модели. Покажите их графическое представление. Простая линейная регрессия имеет вид: Yi = β0 + β1Xi + εi где β0 - сдвиг (длина отрезка, отсекаемого на координатной оси прямой Y), β1 - наклон прямой Y, εi - случайная ошибка переменной Y в i-м наблюдении. В этой модели наклон β1 представляет собой количество единиц измерения переменной Y, приходящихся на одну единицу измерения переменной X. Эта величина характеризует среднюю величину изменения переменной Y (положительного или отрицательного) на заданном отрезке оси X. Сдвиг β0 представляет собой среднее значение переменной Y, когда переменная X равна 0. Последний компонент модели εi является случайной ошибкой переменной Y в i-м наблюдении. 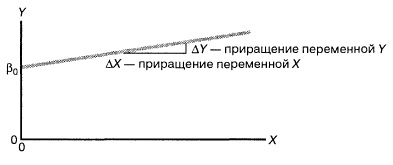 4. Что оценивает линейный коэффициент корреляции? Линейный коэффициент корреляции измеряет степень линейной зависимости между двумя переменными, одна из которых - результативный показатель (у), а другая - факторный (х). 5. Приведите примеры нелинейных моделей по объясняющей переменной x. Модели нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам: Полиноминальное уравнение регрессии(полиномы различных степеней):  Гиперболическое уравнение регрессии: 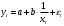 Полулогарифмическое уравнение регрессии:   -случайная ошибка(отклонение, возмущение). -случайная ошибка(отклонение, возмущение).6. Что понимается под линеаризацией нелинейной модели? Многие важные связи в экономике являются нелинейными, например, ПФ (зависимости между объемом производства, трудом и капиталом и т.д.), функция спроса (зависимости между спросом на какой – либо товар или услуги, доходом населения и ценами на этот товар). Если в результате анализа пришли к выводу, что в регрессионной модели функция Такая процедура называется линеаризацией модели. 7. Каким показателем характеризуется теснота связи факторов для нелинейной модели? Каковы свойства этого показателя? Теснота связи факторов для нелинейной модели характеризуется корреляционным отношением. Различают эмпирическое и теоретическое корреляционное отношение. Эмпирическое корреляционное отношение рассчитывается по данным группировки. При отклонении парной статистической зависимости от линейной коэффициент корреляции теряет свой смысл, как характеристика тесноты связи. В этом случае можно воспользоваться таким измерителем связи, как индекс корреляции (корреляционное отношение). Корреляционное отношение применяется в случае нелинейной зависимости между признаками и определяется через отношение межгрупповой дисперсии к общей дисперсии. Для определения эмпирического корреляционного отношения совокупность значений результативного признака У разбивают на отдельные группы. В основу группировки кладется исследуемый фактор Х. Когда изучаемая совокупность (в виде корреляционной таблицы) разбивается на группы по одному (факторному) признаку Х, то для каждой из этих групп можно вычислить соответствующие групповые средние результативного признака. Изменение групповых средних от группы к группе свидетельствует о наличии связи результативного признака с факторным признаком, а примерное равенство групповых средних – об отсутствии связи. Следовательно, чем большую роль в общем изменении результативного признака играет изменение групповых средних (за счет влияния факторного признака), тем сильнее влияние этого признака. Величина корреляционного отношения изменяется от 0 до 1. Близость ее к нулю говорит об отсутствии связи, близость к единице – о тесноте связи. Оценка связи на основе теоретического корреляционного отношения (шкала Чеддока):
Практическая работа № 2 Линейное программирование Целевая функция – максимум прибыли, расход и ресурсные ограничения по видам сырья.  Задаем ограничения: x1+3x2 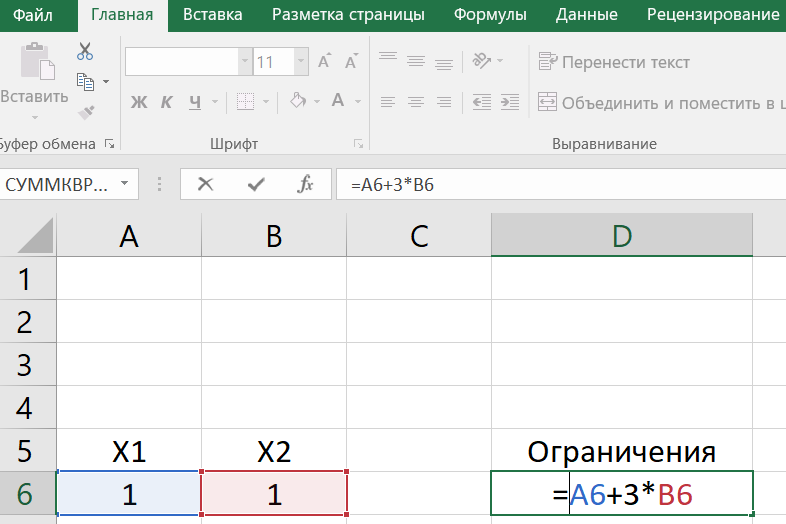 2x1+x2 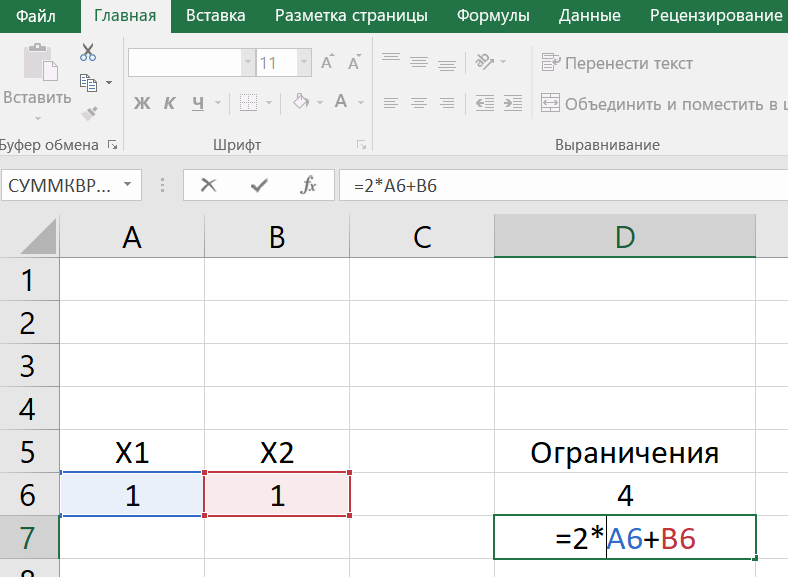 Задаем целевую функцию:  Настраиваем «Поиск решения» 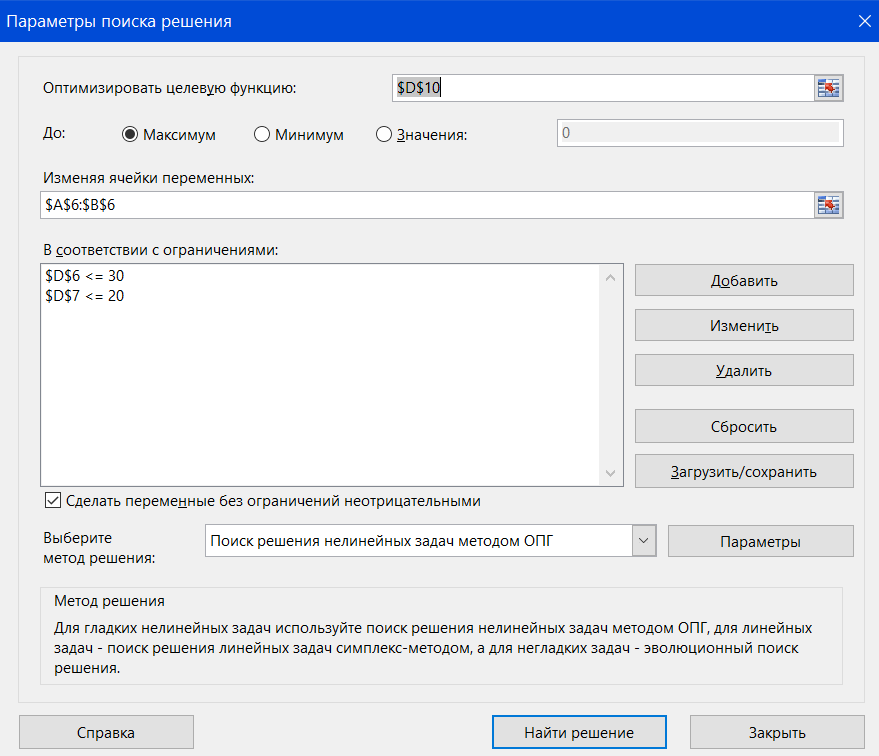 Получаем решение: 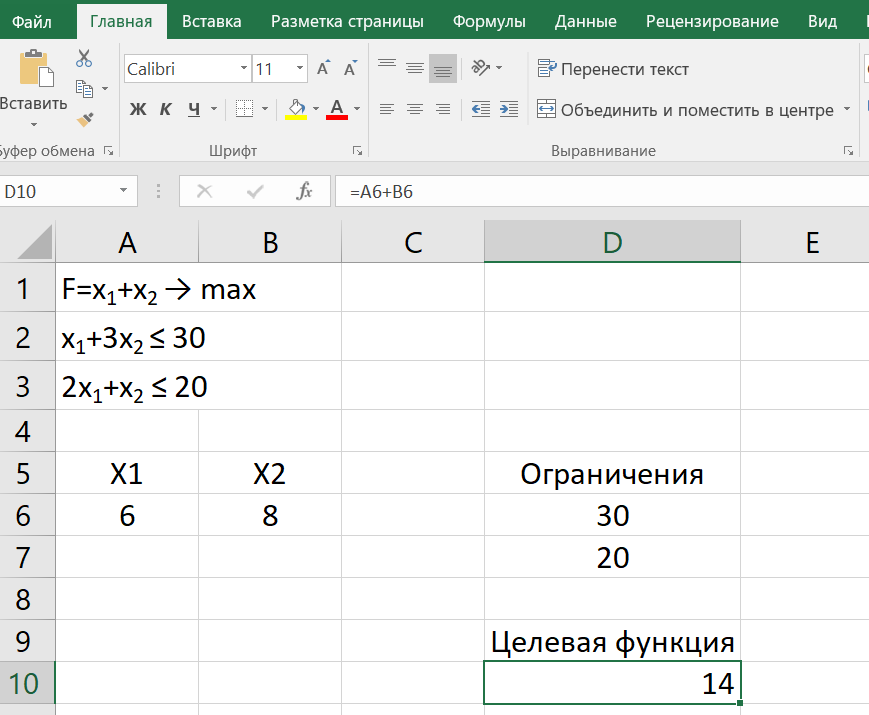 Вопросы для проверки: 1. Назовите основные методы решения ЗЛП. Графический метод решения задачи линейного программирования основан на геометрической интерпретации ЗЛП и применяется в основном при решении задач двумерного пространства и только некоторых задач трёхмерного пространства, так как довольно трудно построить многогранник решений, который образуется в результате пересечения полупространств. Задачу пространства размерности больше трёх изобразить графически вообще невозможно Наиболее известным и широко применяемым на практике для решения общей ЗЛП является симплекс-метод. Несмотря на то, что симплекс-метод является достаточно эффективным алгоритмом, показавшим хорошие результаты при решении прикладных задач ЛП, он является алгоритмом с экспоненциальной сложностью. Причина этого состоит в комбинаторном характере симплекс-метода, последовательно перебирающего вершины многогранника допустимых решений при поиске оптимального решения. Первый полиномиальный алгоритм, метод эллипсоидов, был предложен в 1979 г. советским математиком Л. Хачияном, разрешив таким образом проблему, долгое время остававшуюся нерешённой. Метод эллипсоидов имеет совершенно другую, нежели симплекс-метод, некомбинаторную природу. Однако в вычислительном плане этот метод оказался неперспективным. Тем не менее, сам факт полиномиальной сложности задач привёл к созданию целого класса эффективных алгоритмов ЛП — методов внутренней точки, первым из которых был алгоритм Н. Кармаркара, предложенный в 1984 году. Алгоритмы этого типа используют непрерывную трактовку ЗЛП, когда вместо перебора вершин многогранника решений ЗЛП осуществляется поиск вдоль траекторий в пространстве переменных задачи, не проходящих через вершины многогранника. 2. Поясните суть симплекс-метода решения ЗЛП. Суть симплекс-метода заключается в том, что решение ЗЛП осуществляется итерационно и основывается на переходе от одного допустимого базисного решения к другому, при котором значение целевой функции улучшается. Этот процесс длится до тех пор, пока дальнейшее улучшение целевой функции станет невозможно. В алгебраических терминах симплекс-метод предполагает: 1) умение находить начальный опорный план; 2) наличие признака оптимальности опорного плана; 3) умение переходить к нехудшему опорному плану. Геометрический смысл симплекс-метода состоит в последовательном переходе от одной вершины многогранника ОДР к соседней, в которой целевая функция принимает лучшее значение, до тех пор, пока не будет найдено оптимальное решение. Симплексный метод универсален, поскольку позволяет решить любую ЗЛП. |
