ОСНОВЫ МАТЕМАТ МОДЕЛ. Основы математического моделирования социально экономических процессов
 Скачать 1.42 Mb. Скачать 1.42 Mb.
|
|
Вопросы для проверки: 1. Объясните, в чем суть прогнозирования экономических процессов на основе метода динамических рядов? Суть прогнозирования экономических процессов на основе метода динамических рядов заключается в анализе и статистическом описании динамики какого-либо существенного колеблющегося показателя. Прогнозирование экономических процессов на основе метода динамических рядов начинается с выявления формы его тренда. После этого приступают к статистической оценке параметров тренда. В соответствии с определением тренда, форма его объективна и отражает закономерности развития изучаемого процесса. Задача исследователя заключается в выявлении реально существующей формы тренда, а затем уже в выборе того уравнения (типа линии), которое наилучшим образом аппроксимирует объективный тренд. С позиций признания объективного характера формы тренда исходный пункт исследования самого процесса развития заключается в выявлении его материальной природы, внутренних причин развития и его внешних условий. Такое исследование может установить ожидаемую форму тренда. Теоретический анализ тренда дополняется исследованием его формы по фактическому динамическому ряду, что позволяет выявить тип тренда и измерить его конкретные параметры. 2. Какие компоненты входят в состав динамического ряда? При анализе динамических рядов используется также понятие сезонности (цикличности), характеризующее какие-либо периодические колебания данного ряда, и понятие случайного отклонения под воздействием каких-либо случайных факторов. В общем случае каждый член динамического ряда { Yt }, где t существует в интервале от 1 до T, может быть представлен в аддитивной форме, содержащей несколько составляющих: Yt Ut Vt Et Zt nt, где Ut - тренд динамического ряда – регулярная компонента, характеризующая общую тенденцию; Vt - сезонная компонента или внутригодичные колебания, а в общем случае – циклическая составляющая; Et - случайная компонента, образующаяся под влиянием различных неизвестных причин; Zt - компонента, обеспечивающая сопоставимость элементов динамического ряда; nt - управляющая компонента, с помощью которой воздействуют на члены динамического ряда с целью формирования в будущем его желаемой траектории (управляемый прогноз). 3. Каким образом происходит расчет каждой из составляющих ряда? Вычисление регулярной компоненты Ut (тренда). Известны несколько методов вычисления регулярной компоненты. К ним относятся: механические способы сглаживания, аналитические методы с применением определенных математических функций и, наконец, комбинированный способ. Расчет компоненты Zt Имеется временной ряд данных по месяцам за несколько лет. Примем, что в каждом месяце 25 рабочих дней. Введем следующие обозначения: rt - фактическое число рабочих дней в определенном месяце; T - принятое количество рабочих дней в каждом месяце ( T = 25); Yt - значение ряда в месяце t; Yt1- значение ряда, соответствующее 25 рабочим дням в месяце. Компонента Zt может быть вычислена как: Вычисление сезонной Vt и случайной Et компонент. Для определения сезонной и случайной компонент вычисляется динамический ряд: Vt Et Yt (Ut Zt), при nt =0. Сезонная и случайная компоненты представляют собой составляющие временного ряда, которые остаются после выделения из него тренда и выравнивающей компоненты, при условии, что управляющая компонента равна нулю. При разделении сезонной и случайной компонент обычно первой вычленяют сезонную компоненту, а оставшуюся часть временного ряда относят к случайной составляющей. Среднесезонное значение может быть найдено как Для нахождения случайной составляющей Et временной ряд следует привести к сопоставимому виду, сезонную компоненту и тренд необходимо отфильтровать и вычесть из значений Yt, управление nt должно отсутствовать. 4. Как оценить адекватность трендовой модели? Модель тенденции считается адекватной реальному процессу, если теоретические (найденные по уравнению тренда) уровни ряда достаточно близко подходят к фактическим их значениям, т.е. 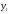 и и 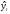 мало отличаются друг от друга. Для оценки адекватности модели проводится анализ остатков мало отличаются друг от друга. Для оценки адекватности модели проводится анализ остатков 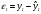 . .Модели тенденции также можно сравнивать по величине остаточной суммы квадратов: 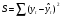 . Чем меньше эта величина, тем в большей степени уравнение тренда подходит для описания тенденции временного ряда. . Чем меньше эта величина, тем в большей степени уравнение тренда подходит для описания тенденции временного ряда.Другим показателем при выборе функции тренда является коэффициент детерминации R2. Чем выше R2, тем выше вероятность того, что данная модель тенденции описывает исходные данные. Величина 1- R2 отражает влияние случайной составляющей, т.е. показывает, какая доля вариации уровней динамического ряда не связана с тенденцией. Однако рассмотренные критерии адекватности модели тенденции (S и R2) могут привести к неправильным выводам, если не учитывать статистическую значимость параметров уравнения тренда. Уравнение тренда хорошо описывает тенденцию, если отсутствует автокорреляция в остатках, т.е. остатки текущего периода не коррелируют с остатками предыдущего периода. Измерить автокорреляцию в остатках можно с помощью коэффициента автокорреляции остатков: Чем ближе коэффициент автокорреляции остатков 5. Почему рекомендуют автоматизировать работы по прогнозированию при разработке управленческих решений? Работы по прогнозированию при разработке управленческих решений рекомендуется автоматизировать, так как обычно прогнозирование опирается на рутинные расчеты, выполнение которых вручную требует значительных затрат времени и которые приводят к различным просчетам и ошибкам. Во время ручной работы не остается достаточного времени для поиска оптимальных вариантов, поэтому планирование ограничивается первым непротиворечивым планом. С помощью автоматизации сокращается время поиска варианта, а также реализуется возможность проведения их сравнительного анализа. Практическая работа № 5 Планирование эксперимента. Полный факторный эксперимент. Методические указания по выполнению лабораторной работы  При планировании двухфакторного эксперимента были вычислены параметры линейной модели, линейной модели со смешанными оценками и нелинейной модели, построены графики функций. Согласно графикам функций адекватными моделями являются линейная модель и модель со смешанными оценками. При оценке адекватности моделей по значениям сумм квадратов отклонений также можно сделать вывод, что линейная модель(сумма квадратов отклонений равна 0,84) и модель со смешанными оценками(сумма квадратов отклонений равна 0,78) являются адекватными и наиболее точно описывают экспериментальную функцию. Вопросы для проверки: 1. Как рассчитать число серий эксперимента N? Для полного факторного эксперимента, в котором реализуются все возможные сочетания уровней факторов, число опытов определяется по следующей формуле: N = Ak , где N - число опытов; k - число факторов, A-число уровней Для двухуровневого эскперимента формула имеет вид: N = 2k 2. Чем отличается линейная модель, нелинейная модель и линейная модель со смешанными оценками? При планировании эксперимента следует начинать с линейной модели (Yлин = A0 +A1*X1+A2*X2). Если результаты не будут удовлетворять поставленным требованиям, то необходимо перейти к рассмотрению более сложных моделей. Линейная и линейная модель со смешанными(Y лс = A0 +A1*X1+A2*X2 +A12*X1*X2) оценками требуют изменения факторов на двух уровнях. Линейная модель со мешанными оценками отличается от линейной модели наличием дополнительного слагаемого A12*X1*X2, отражающего взаимодействие двух факторов. Такие эффекты взаимодействия, хотя и малы по сравнению с линейными, но все же не равны нулю. Нелинейная модель (Y н = A0 +A1*X1+A2*X2 +A12*X1*X2 + +A11*X1^2 + A22*X2^2) – описывается тремя уровнями изменения факторов и учитывает взаимодействие факторов, находящихся на разных уровнях. 3. Как оценить адекватность моделей? Числом степеней свободы в статистике называется разность между числом опытов и числом коэффициентов (констант), которые уже вычислены по результатам этих опытов независимо друг от друга. Остаточная сумма квадратов, деленная на число степеней свободы, называется остаточной дисперсией, или дисперсией адекватности  . .В статистике разработан критерий, который очень удобен для проверки гипотезы об адекватности модели. Он называется F-критерием Фишера и определяется следующей формулой: Удобство использования критерия Фишера состоит в том, что проверку гипотезы можно свести к сравнению с табличным значением. Если рассчитанное значение F-критерия не превышает табличного, то, с соответствующей доверительной вероятностью, модель можно считать адекватной. При превышении табличного значения эту гипотезу приходится отвергать. Этот способ расчета дисперсии адекватности, подходит, если опыты в матрице планирования не дублируются, а информация о дисперсии воспроизводимости извлекается из параллельных опытов в нулевой точке или из предварительных экспериментов. Важны два случая: 1) опыты во всех точках плана дублируются одинаковое число раз (равномерное дублирование), 2) число параллельных опытов не одинаково (неравномерное дублирование). В первом случае дисперсию адекватности нужно умножать на n, где n – число повторных опытов  . .Такое видоизменение формулы вполне естественно. Чем больше число параллельных опытов, тем с большей достоверностью оцениваются средние значения. Поэтому требования к различиям между экспериментальными и расчетными значениями становятся более жесткими, что отражается в увеличении F-критерия. Во втором случае, когда приходится иметь дело с неравномерным дублированием, положение усложняется. Даже когда экспериментатор задумал провести равное число параллельных опытов, часто не удается по тем или иным причинам все их реализовать. Кроме того, иногда приходится отбрасывать отдельные опыты как выпадающие наблюдения. При неравномерном дублировании нарушается ортогональность матрицы планирования и, как следствие, изменяются расчетные формулы для коэффициентов регрессии и их ошибок, а также для дисперсии адекватности. Для дисперсии адекватности можно записать общую формулу  , ,где N – число различных опытов (число строк матрицы); ni – число параллельных опытов в i-й строке матрицы; Смысл этой формулы очень прост: различию между экспериментальным и расчетным значением придается тем больший вес, чем больше число повторных опытов. Для b-коэффициентов нельзя записать универсальную расчетную формулу. Все зависит от того, какой был план и как дублировались опыты. Всякий раз приходится делать специальные расчеты, пользуясь методом наименьших квадратов. Практическая работа № 6 Теория массового обслуживания Задание Одноканальная СМО с отказами представляет собой одну телефонную линию. Заявка – вызов, пришедший в момент, когда линия занята, получает отказ. Интенсивность потока вызовов λ=0,7 (вызовов в минуту). Средняя продолжительность разговора 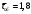 мин. Все потоки событий – простейшие. Определить предельные (при мин. Все потоки событий – простейшие. Определить предельные (при 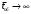 ) значения: ) значения:Относительной пропускной способности q; Абсолютной пропускной способности A; Вероятности отказа Pотк Сравнить фактическую пропускную способность СМО с номинальной, которая была бы, если бы каждый разговор длился в точности 1,8 мин, и разговоры следовали бы один за другим без перерыва. Решение: Определяем параметр µ потока обслуживаний: 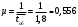 . .Вычислим относительную пропускную способность q: 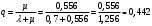 . .Таким образом, в установившемся режиме система будет обслуживать около 44% поступающих вызовов. Находим абсолютную пропускную способность: 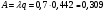 , , Т.е. линия способна осуществить в среднем 0,309 разговоров в минуту. Вероятность отказа: 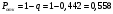 , ,Значит, около 56% поступивших вызовов будет получать отказ Номинальная пропускная способность канала: 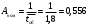 (разговора в минуту), (разговора в минуту),Что почти вдвое больше(в 1,8 раз), чем фактическая пропускная способность, полученная с учетом случайного характера потока заявок и случайности времени обслуживания. Вопросы для проверки: 1. Охарактеризуйте системы массового обслуживания. Системы массового обслуживания (СМО) – класс математических схем, разработанных в теории массового обслуживания и различных приложениях для формализации процессов функционирования систем, которые по своей сути являются процессами обслуживания.Характерным для работы таких систем является случайное появление заявок на обслуживание и завершение обслуживания случайные моменты времени, то есть стохастический характер их функционирования.В любом элементарном акте обслуживания можно выделить две основные составляющие: ожидание обслуживания заявкой и само обслуживание заявки. Основными элементами СМО являются входной поток заявок, входной поток обслуживаний, очереди заявок, ожидающих обслуживания, каналы обслуживания и выходной поток обслуженных заявок и заявок, которым по тем или иным причинам в обслуживании отказано. СМО классифицируют по следующим признакам: а) по количеству каналов обслуживания они делятся на одноканальные и многоканальные СМО; б) по организации ожидания заявки – на системы с отказами и системы с ожиданием или с очередями (накопителями) в) СМО с накопителями, в свою очередь, делятся на системы с приоритетами и без приоритетов; г) по количеству фаз обслуживания – на однофазные и многофазные; д) по взаимосвязи с потоками заявок – на разомкнутые и замкнутые. Эффективность работы СМО характеризуется следующими основными показателями: абсолютная пропускная способность – среднее количество заявок, которое может обслужить система в единицу времени; относительная пропускная способность – отношение среднего числа заявок, обслуженных СМО в единицу времени, к среднему числу всех заявок, поступивших в СМО за это же время; коэффициент занятости – отношение среднего числа занятых каналов к общему числу каналов; коэффициент простоя – отношение среднего числа свободных каналов к общему числу каналов. 2. Как рассчитать вероятность отказа? Вероятность отказа СМО определяется по формуле: 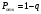 , где q- это относительная пропускная способность. , где q- это относительная пропускная способность.3. Как рассчитать пропускную способность системы? Относительную пропускную способность q можно рассчитать по формуле 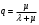 , где λ - интенсивность потока заявок, , где λ - интенсивность потока заявок, 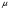 – это среднее число заявок – это среднее число заявок Абсолютная пропускная способность рассчитывается по формуле: 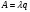 , где λ - интенсивность потока заявок, q - относительная пропускная способность , где λ - интенсивность потока заявок, q - относительная пропускная способность |
