ОСНОВЫ МАТЕМАТ МОДЕЛ. Основы математического моделирования социально экономических процессов
 Скачать 1.42 Mb. Скачать 1.42 Mb.
|
|
3. Поясните суть графического решения ЗЛП. Этот метод применяется для решения ЗЛП с двумя переменными, заданными в неканонической форме и многими переменными в канонической форме, при условии, что они содержат не более двух свободных переменных. Метод основывается на возможности графического изображения области допустимых решений задачи и нахождении среди них оптимального решения(ОДР). ОДР задачи – это ОДР системы неравенств и равенств ограничений. Для нахождения среди ДР оптимального решения используют линии уровня и опорные прямые. Линией уровня называется прямая, на которой целевая функция задачи принимает постоянное значение. Уравнение линии уровня в общем случае имеет вид 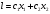 . Все линии уровня параллельны между собой. Их нормаль . Все линии уровня параллельны между собой. Их нормаль4. Могут ли ответы в решении ЗЛП быть отрицательными и почему? Если все оценки индексной строки (строки целевой функции) не отрицательны, то соответствующий план является оптимальным в задаче максимизации. Признак оптимальности задачи минимизации: Если все оценки индексной строки (строки целевой функции) не положительны, то соответствующий план является оптимальным в задаче минимизации. 5. Какие ресурсные ограничения используются в задачах ЗЛП? Основными ресурсными ограничениями в задачах ЗЛП являются материальные ресурсы(деньги, материалы, сырье), время, рабочая сила. Практическая работа № 3 Транспортная задача. Задание: Определить оптимальный план перевозок с минимальными затратами для исходных данных, приведенных ниже. 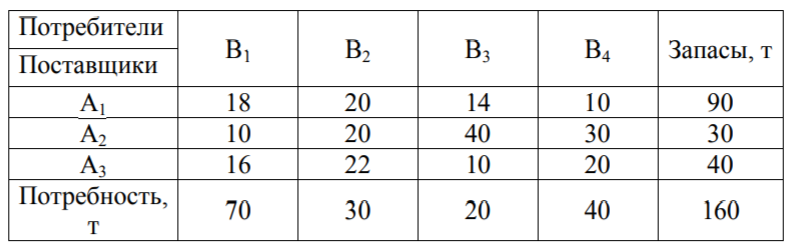 Указываем тарифы на перевозку единицы товара от каждого поставщика к каждому потребителю: 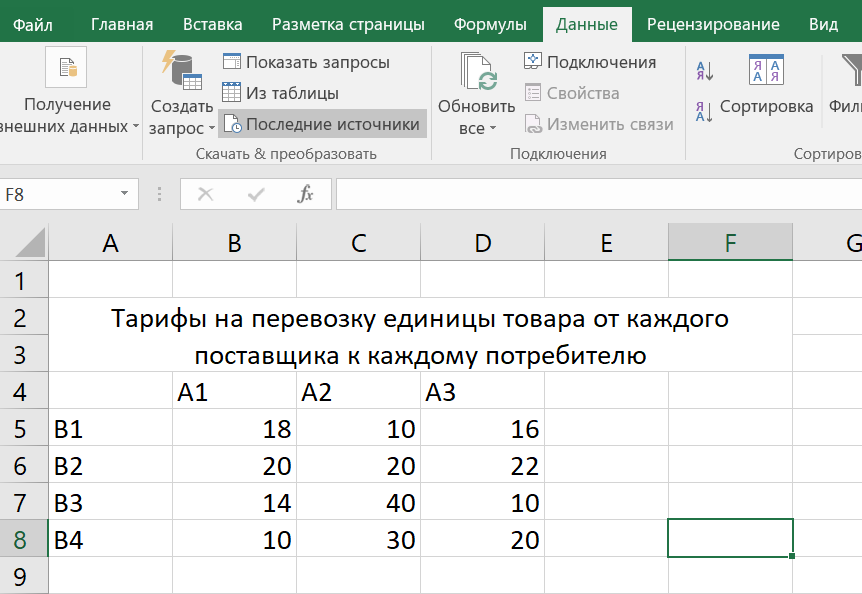 Настраиваем «Поиск решения» 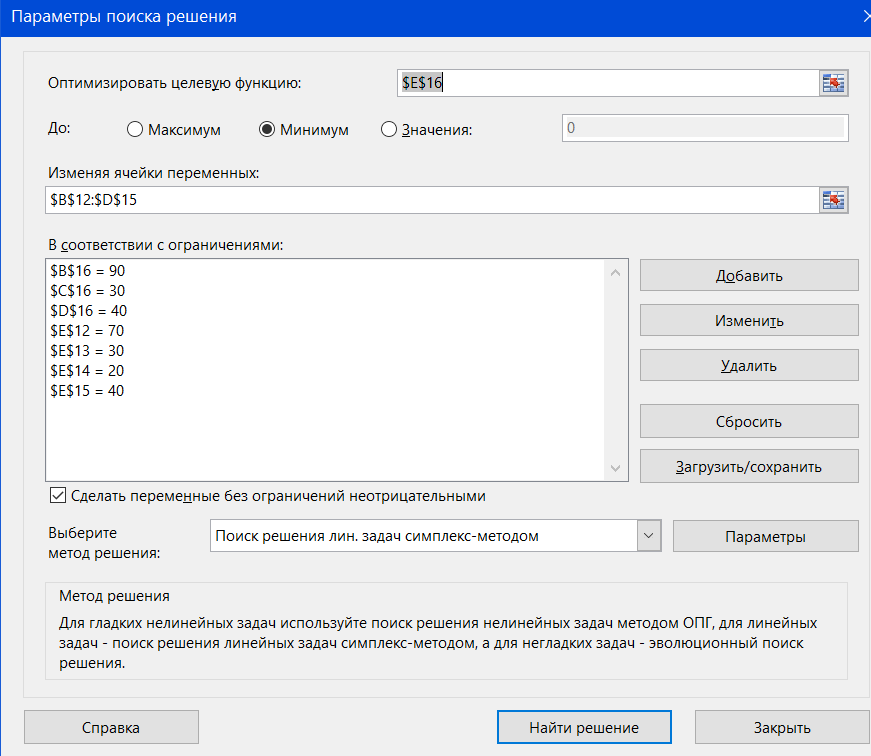 Получаем оптимальные объемы перевозок и минимальное значение целевой функции: 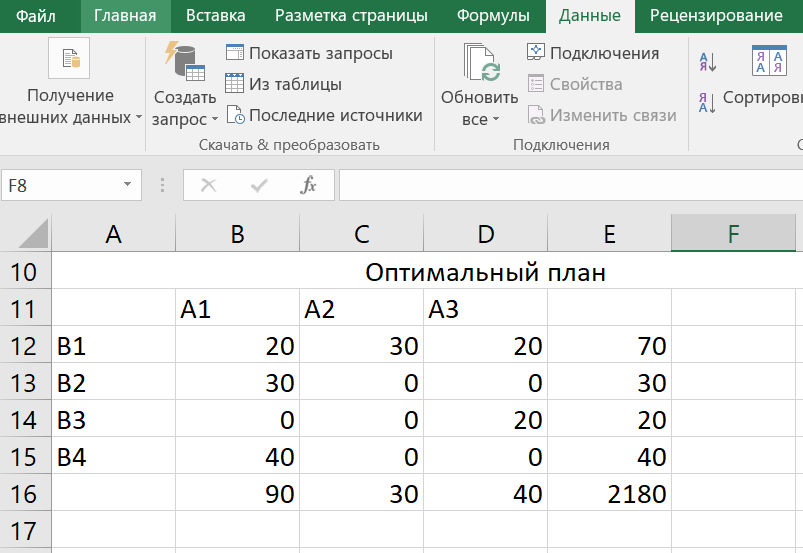 Вопросы для проверки: 1. Какие задачи линейного программирования называются транспортными? Транспортная задача – это задача об оптимальном плане перевозок однородного продукта из однородных пунктов наличия в однородные пункты потребления на однородных транспортных средствах (предопределённом количестве) со статичными данными и линеарном подходе (это основные условия задачи). Для классической транспортной задачи выделяют два типа задач: критерий стоимости (достижение минимума затрат на перевозку) или расстояний и критерий времени (затрачивается минимум времени на перевозку). Под названием транспортная задача, определяется широкий круг задач с единой математической моделью, эти задачи относятся к задачам линейного программирования и могут быть решены оптимальным методом. Однако, специальный метод решения транспортной задачи позволяет существенно упростить её решение, поскольку транспортная задача разрабатывалась для минимизации стоимости перевозок. 2. Каковы особенности математической модели транспортной задачи? Однородный груз сосредоточен у m поставщиков в объемах 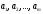 Данный груз необходимо доставить n потребителям в объемах Данный груз необходимо доставить n потребителям в объемах 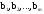 . Известны . Известны 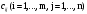 - стоимости перевозки единицы груза от каждого i-го поставщика каждому j-му потребителю. Требуется составить такой план перевозок, при котором запасы всех поставщиков вывозятся полностью, запросы всех потребителей удовлетворяются полностью и суммарные затраты на перевозку всех грузов минимальны. - стоимости перевозки единицы груза от каждого i-го поставщика каждому j-му потребителю. Требуется составить такой план перевозок, при котором запасы всех поставщиков вывозятся полностью, запросы всех потребителей удовлетворяются полностью и суммарные затраты на перевозку всех грузов минимальны.Исходные данные транспортной задачи записываются в таблице вида:
Переменными (неизвестными) транспортной задачи являются 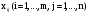 - объемы перевозок от каждого i-го поставщика каждому j-му потребителю. Они могут быть записаны в виде матрицы перевозок. - объемы перевозок от каждого i-го поставщика каждому j-му потребителю. Они могут быть записаны в виде матрицы перевозок.Математическая модель транспортной задачи в общем случае: 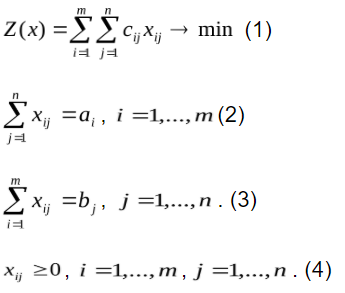 Целевая функция задачи (1) выражает требование обеспечить минимум суммарных затрат на перевозку всех грузов. Первая группа из т уравнений (2) описывает тот факт, что запасы всех т поставщиков вывозятся полностью. Вторая группа из п уравнений (3) выражает требование полностью удовлетворить запросы всех п потребителей. Неравенства (4) являются условиями неотрицательности всех переменных задачи. Таким образом, математическая формулировка транспортной задачи состоит в следующем: найти переменные задачи 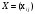 удовлетворяющие системе ограничений (2), (3), условиям неотрицательности (4) и обеспечивающие минимум целевой функции (1). В рассмотренной модели транспортной задачи предполагается, что суммарные запасы поставщиков равны суммарным запросам потребителей, т.е. удовлетворяющие системе ограничений (2), (3), условиям неотрицательности (4) и обеспечивающие минимум целевой функции (1). В рассмотренной модели транспортной задачи предполагается, что суммарные запасы поставщиков равны суммарным запросам потребителей, т.е.Такая задача называется задачей с правильным балансом, а ее модель — закрытой. Если же это равенство не выполняется, то задача называется задачей с неправильным балансом, а ее модель — открытой. Для того чтобы транспортная задача линейного программирования имела решение, необходимо и достаточно, чтобы суммарные запасы поставщиков равнялись суммарным запросам потребителей (см. равенство (5)), т.е. задача должна быть с правильным балансом. 3. Какие транспортные задачи называются открытыми и закрытыми? Модель ТЗ называют закрытой (сбалансированной), если суммарный объем груза, имеющегося у поставщиков, равен суммарному спросу потребителей, т. е. выполняется равенство: 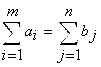 Если для транспортной задачи выполняется одно из условий: 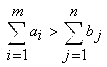 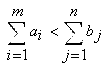 То модель задачи называют открытой (несбалансированной). Для разрешимости ТЗ с открытой моделью необходимо преобразовать ее в закрытую модель. 4. Могут ли объемы перевозок быть отрицательными? Объемы перевозок не могут быть отрицательными. 5. В чем особенность целевой функции транспортной задачи? Целевая функция транспортной задачи: выражает требование обеспечить минимум суммарных затрат на перевозку всех грузов. Практическая работа № 4 Прогнозирование цен фьючерских контрактов на акции компании
1. Вычислим регулярную составляющую (тренд): а) Рассчитаем среднее значение для каждого года (столбца). Результаты внесем в таблицу 3.2. 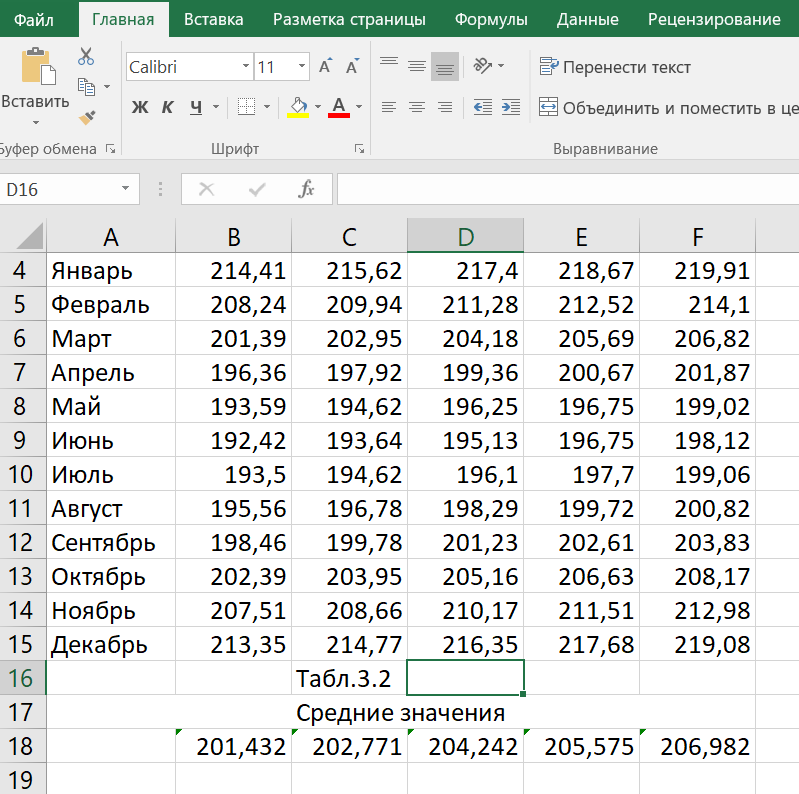 б) Построим график изменения средних значений объемов продаж, перебирая типы уравнений регрессии. Наиболее точно описывающее точки из таблицы является линейная регрессия вида: y = 1,3904x + 200,03. Коэффициенты уравнения записываем рядом с графиком. 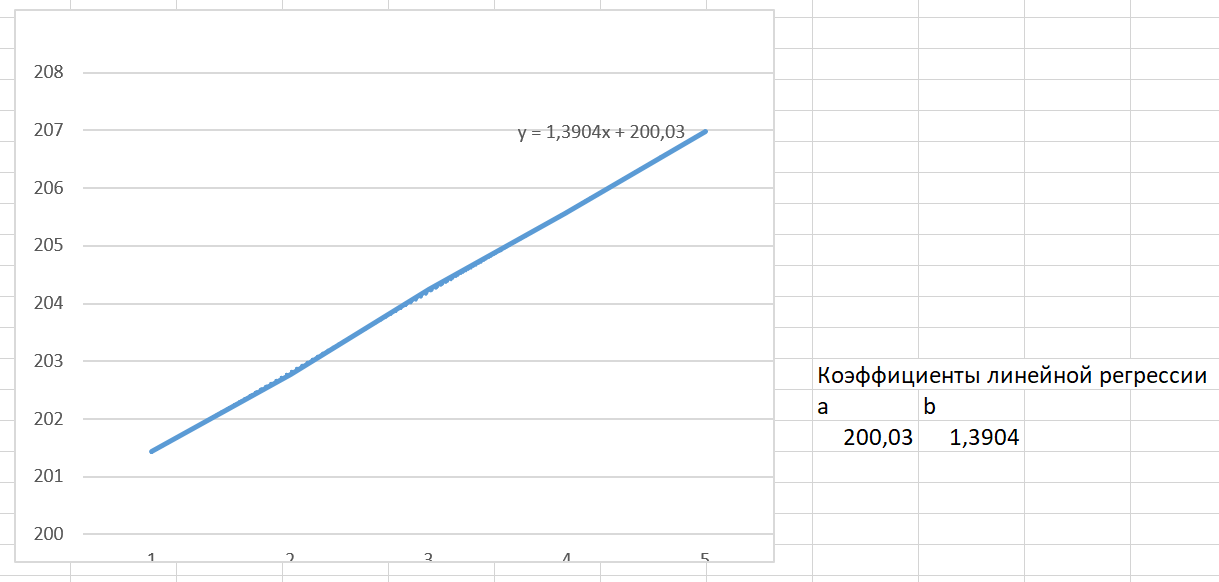 2. Вычислим сезонную компоненту (волну): а) Сформируем таблицу 3.3 вычитанием из таблицы 3.1 соответствующих среднегодовых значений таблицы 3.2. Усредним значения по каждому месяцу и запишем в таблицу 3.3 в соответствии с месяцем в столбец «Средние». 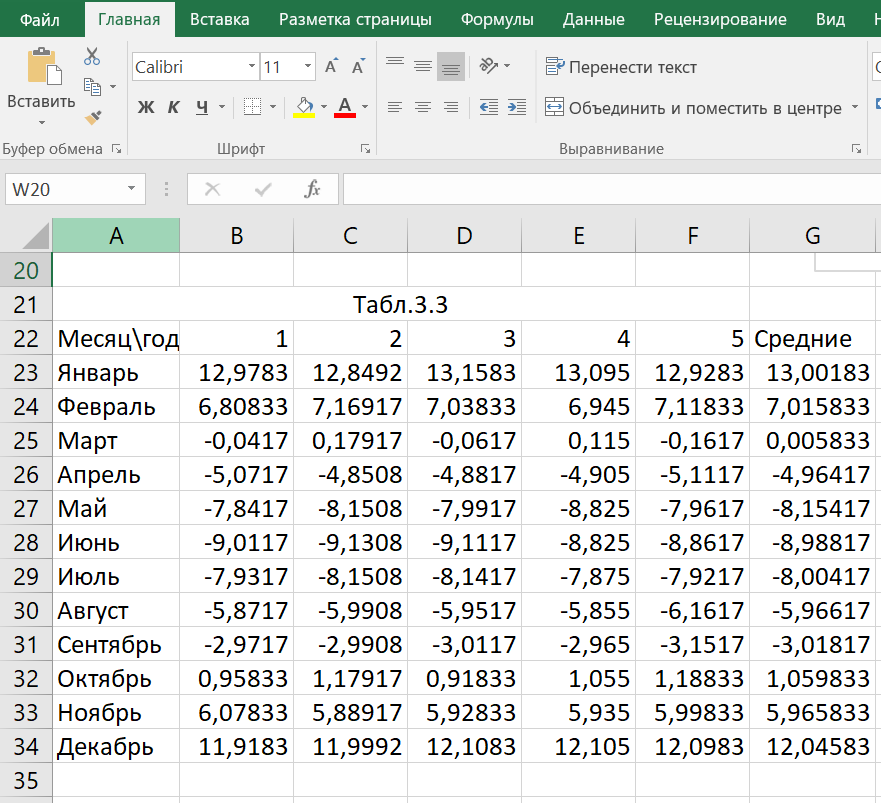 б) С помощью «Мастера Диаграмм» построим график изменения средних значений по месяцам. Вставим линию тренда и подберем тип регрессии. Наилучшим образом описывающая точки графика является полиноминальная регрессия вида: y = 0,7101x2 - 9,2146x + 21,432. Коэффициенты уравнения запишем рядом с диаграммой. 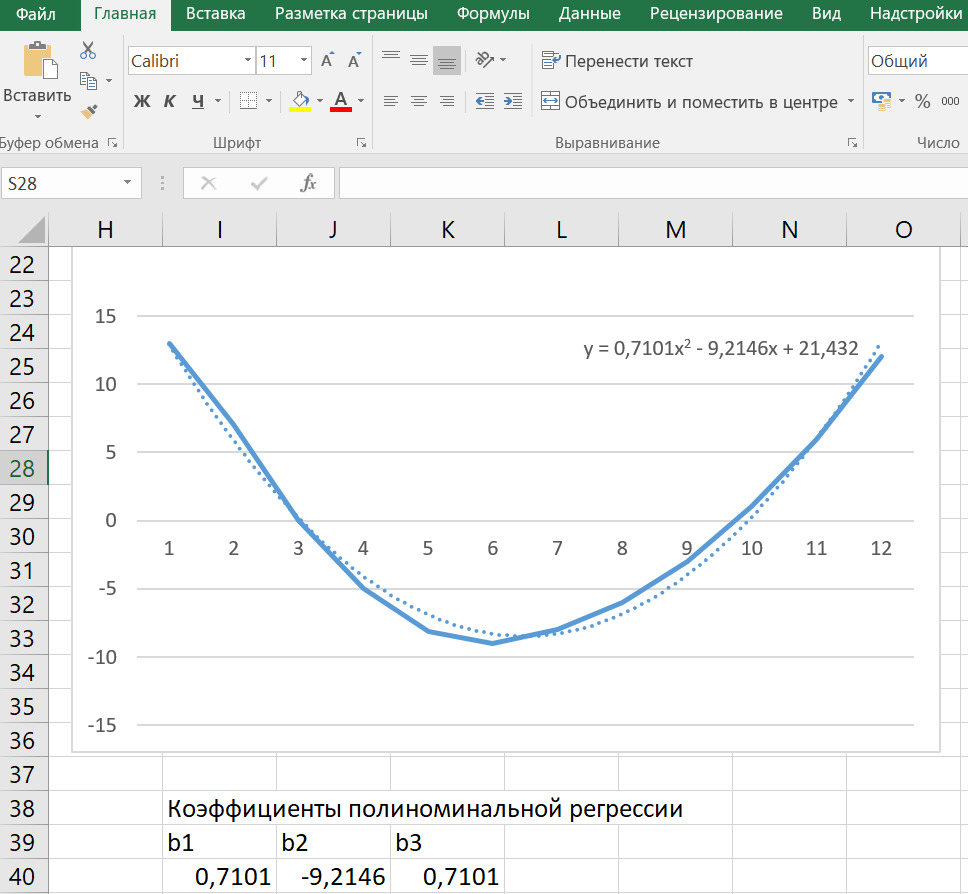 3. Вычислим случайную составляющую. сформируем таблицу 3.4 вычитанием из среднемесячного значения (столбец «средние») всех значений таблицы 3.3 соответствующего месяца. Найдем минимальное (MIN) и максимальное (MAX) значение в таблице 3.4. 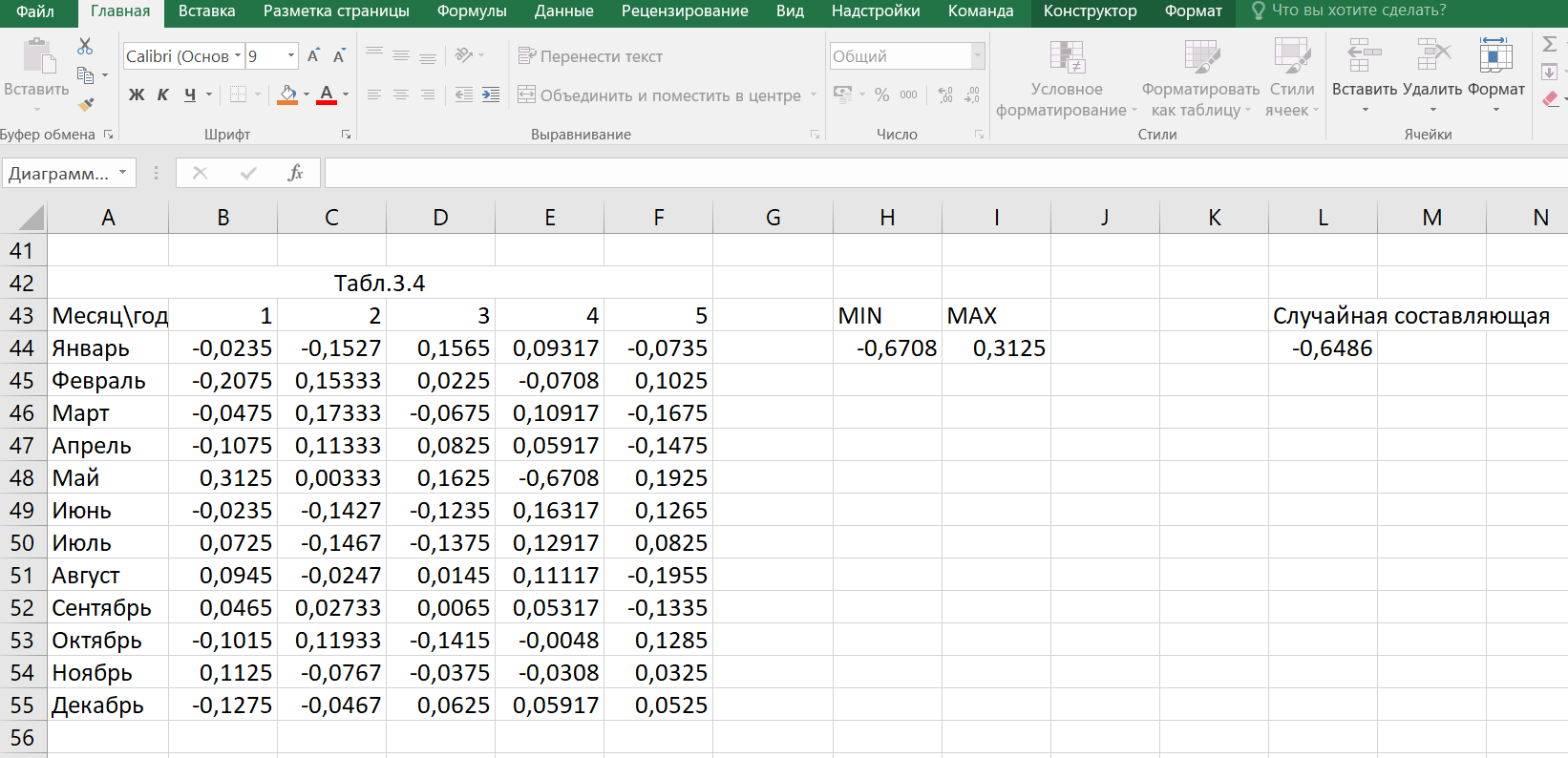 4. Используя полученную модель, сделаем прогноз на февраль будущего года. 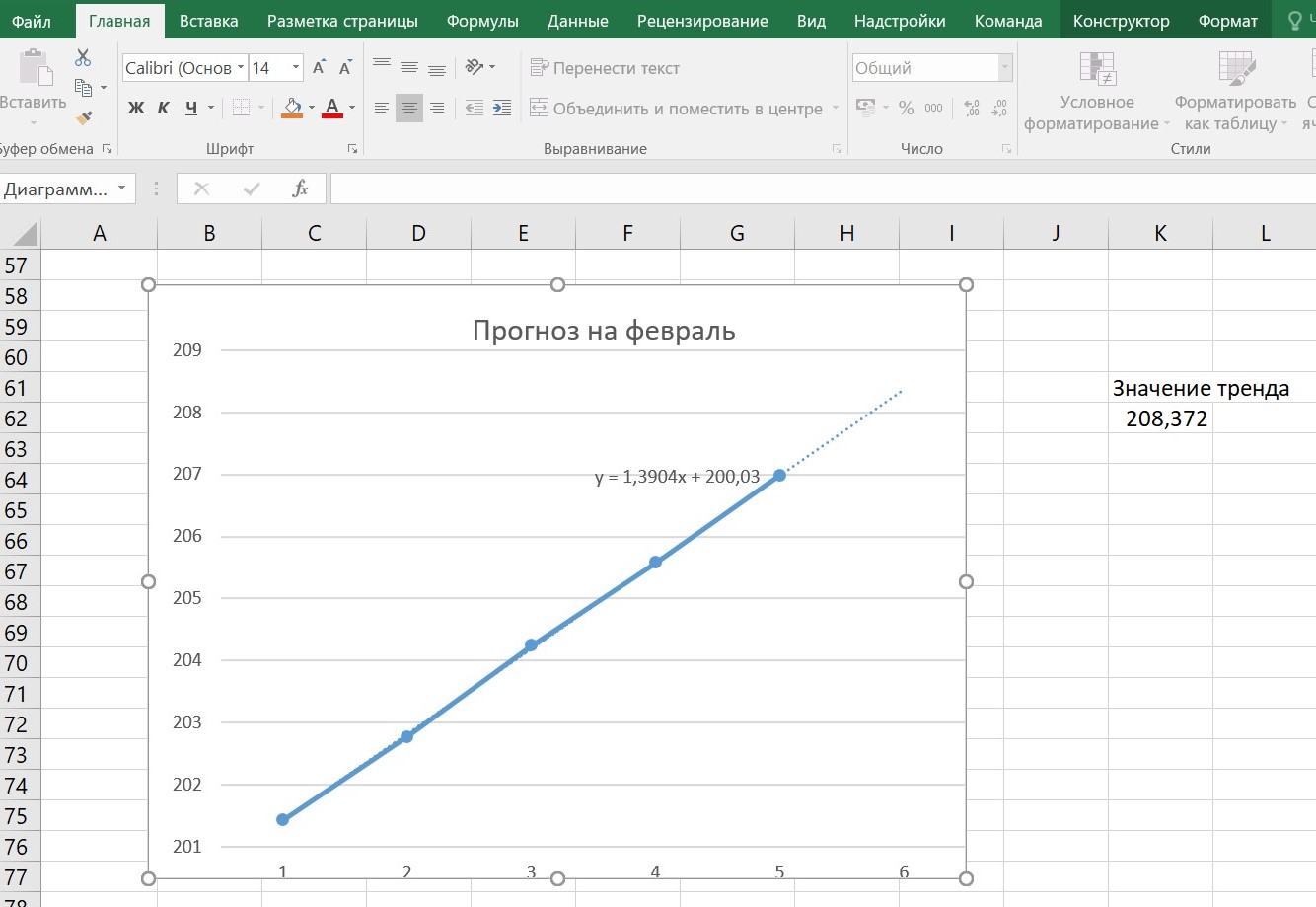 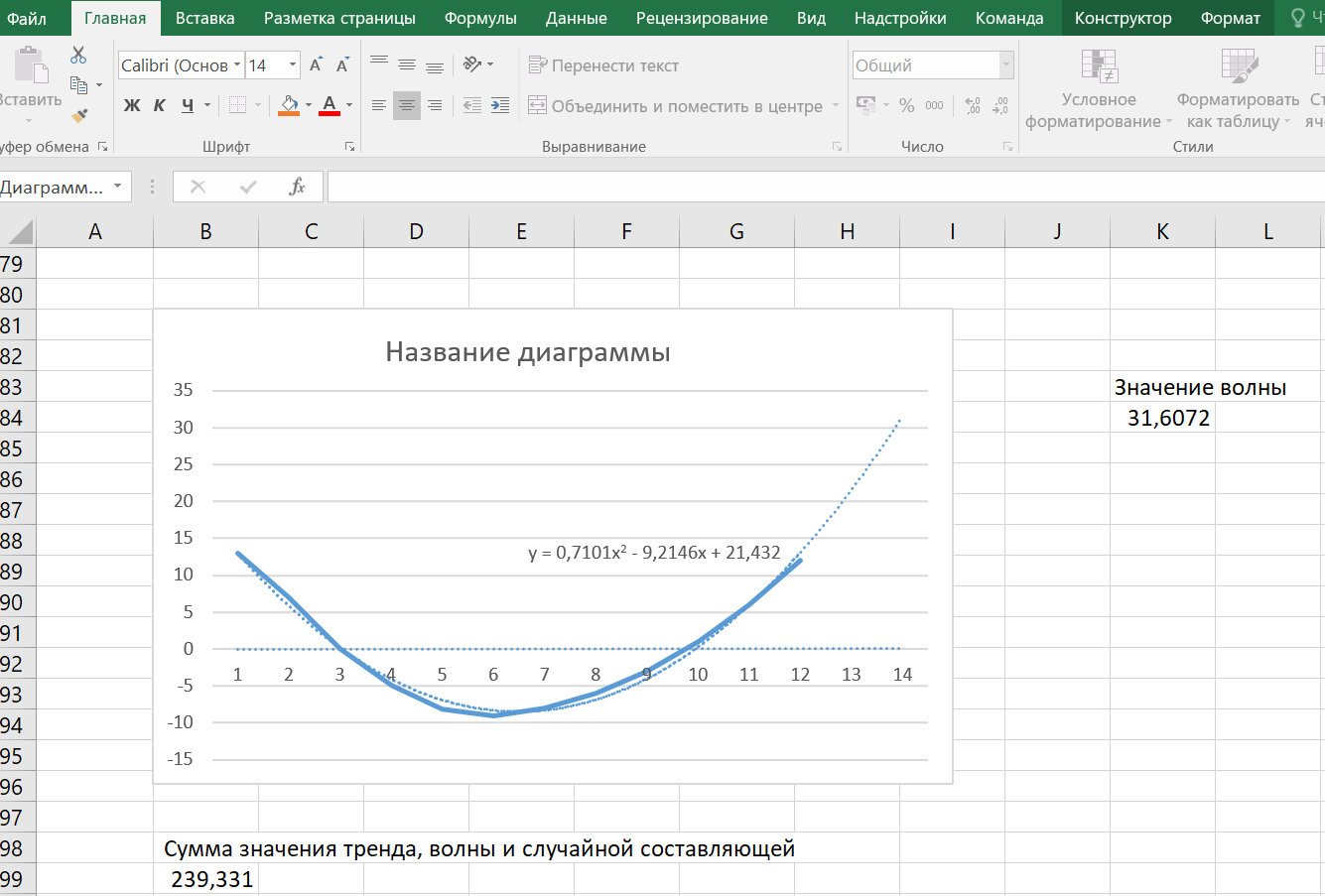 Значение тренда равно 208,372. Значение волны равно 31,6072. После суммирования значений тренда, волны и случайной составляющей получаем прогноз цены на февраль следующего года равный 239,331. Полученная модель с учетом случайной составляющей, сезонной составляющей(волны) и основного направления(тренда) движения цены позволяет Сделать прогноз, что в феврале следующего года цена на акции составит 239,4228. Согласно прогнозу, цена на акции будет расти. Цена на акции в феврале будет иметь максимальное значение за последние 5 лет, согласно прогнозу. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
