поурочные планы математика 4 класс Школа России. поурочные планы математика. Основные требования к знаниям, умениям и навыкам учащихся к концу 4 класса учащиеся должны знать
 Скачать 2.41 Mb. Скачать 2.41 Mb.
|
|
Дети. Надо 360 разделить на 12; число 12 заменили произведением чисел 6 и 2; получится пример: 360 разделить на произведение чисел 6 и 2; 360 разделили на 6, на первый множитель, и результат 60 разделили на 2, на второй множитель, получилось 30. Аналогичным образом объясняют решение другого примера. Учитель замечает, что и здесь делитель заменили произведением удобных множителей. Ученики должны объяснить, почему эти множители удобные (легко делить на 10, на 100, легко разделить 360 на 6). Далее учитель предлагает решить примеры, данные в задании 89, заменяя делитель произведением удобных множителей. При этом выполняется развернутая запись по образцу, данному в задании 88. При выполнении задания 90 ученики записывают решение кратко (320 : 80 = 4) и дают краткое объяснение: «80 заменяю произведением чисел 10 и 8, разделю 320 на 10, получится 32, разделю 32 на 8, получится 4». Ф и з к у л ь т м и н у т к а IV. Работа над пройденным материалом. 1. Решение задач. После чтения задачи 91 учащиеся рассматривают чертеж к ней. Потом составляют план решения. Далее дети работают самостоятельно. Задачу 93 учащиеся решают с комментированием у доски. Длина – 5 м Ширина – 4 м S – ? м2 1 м2 – 250 г Всего лака – ? г 1) S = 5 · 4 = 20 (м2) 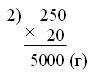 О т в е т: 5 000 г лака потребуется для покрытия пола. V. Итоги урока. Учитель. Ребята, что нового узнали на уроке? Дети. Мы познакомились с новым приемом деления. Учитель. Что повторили на уроке? Дети. Повторили решение задач, перевод единиц длины, массы, времени, площади. Домашнее задание: задания 92, 94; тетрадь № 2, с. 21, № 2, 3. У р о к 101 деление с остатком на 10, 100 и 1000 Цели: познакомить учащихся с приемом деления с остатком на 10, 100 и 1 000; совершенствовать вычислительные навыки, умения решать задачи и уравнения. Ход урока I. Организационный момент. II. Устный счёт. 1. «Цепочка».  2. Задание 99. Сколько раз по 100 м содержится в 2 км? Сколько раз по 10 г содержится в 3 кг? Сколько раз по 15 с содержится в 1 мин? 3. Заполните таблицу. Задание 101 (можно вынести на доску).  III. Работа над новым материалом. Прием деления с остатком на 10 и 100 учитель объясняет на одном из примеров. Учитель. 64 : 10. 64 без остатка не разделится на 10. Возьмем наибольшее число до 64, которое делится на 10, – это 60. Разделим 60 на 10, получим 6. Это частное, а остаток 4. После этого учитель предлагает прочитать объяснение, данное в учебнике на с. 21 вверху. Далее учащиеся решают с объяснением примеры, данные в задании 96, и делают вывод, что при делении на 10 остаток показывает число единиц делимого, а в частном будет число, записанное остальными цифрами делимого; при делении на 100 в остатке будет число, записанное двумя последними цифрами делимого, а в частном число, записанное остальными цифрами делимого. Для того чтобы этот вывод был усвоен сознательно, важно объяснить, почему это так: на 10 можно разделить все содержащиеся в числе десятки, а единицы остаются; аналогично для 100 и 1 000. Ф и з к у л ь т м и н у т к а IV. Работа над пройденным материалом. 1. Решение задач. После чтения задачи 98 учащиеся под руководством учителя записывают ее условие и составляют план решения. Далее дети работают самостоятельно.
1) 168 : 8 = 21 (л) – на 1 га 2) 21 · 20 = 420 (л) – на 20 га 3) 84 : 21 = 4 (га) О т в е т: 420 л надо на 20 га, 4 га можно вспахать, имея 84 л горючего. 2. Решение уравнений. В задании 100 дети составляют по задачам уравнения, решают их самостоятельно (с последующей проверкой). V. Итоги урока. Учитель. Ребята, что нового узнали на уроке? Дети. Мы учились выполнять деление на 10 и 100 с остатком. Учитель. Что закрепляли? Дети. Мы закрепляли решение задач и уравнений. Домашнее задание: задания 97, 102; тетрадь № 2, с. 22, № 4–7. У р о к 102 Решение задач Цели: познакомить учащихся с решением задач на нахождение четвертого пропорционального; совершенствовать представления о неравенствах и равенствах, а также навыки деления с остатком на 10, 100, 1 000 и умение решать задачи на встречное движение. Ход урока I. Организационный момент. II. Устный счёт. 1. Выполните деление с остатком. 427 : 10 2 486 : 100 635 : 10 6 105 : 10 718 : 100 7 130 : 100 2. Решите цепочки примеров.  III. Работа над новым материалом. Работу по решению задачи 103 можно провести так. Учитель. Прочитайте задачу. Рассмотрите рисунок. Что известно о расходе полотна на наволочки? Дети. Из каждых 2 м полотна получается 3 наволочки. Учитель. Что надо узнать? Дети. Сколько таких наволочек получится из 42 м полотна. Учитель. Вы уже решали похожие задачи. Как, по-вашему, можно решить эту задачу? Дети. Сначала узнаем, сколько полотна идет на одну наволочку. Учитель. Как узнаете? Дети. Нужно 2 разделить на 3, но 2 на 3 не делится. Учитель. Как же быть? Выразим 2 м в сантиметрах и разделим на 3. Выполните деление на доске. Дети. Не делится, получается остаток. Учитель. В таких случаях задачу решают по-другому. Рассмотрите запись на рисунке и объясните, как вы понимаете слова «из 2 м полотна получается 3 наволочки». Дети. Если взять 2 м, то получится 3 наволочки, еще 2 м – еще 3 наволочки, пока не израсходуют 42 м полотна. Учитель. Как же узнать, сколько получится наволочек из этих 42 м полотна? Дети. Узнаем, сколько раз в 42 м содержится по 2 м, выполнив деление; потом узнаем, сколько наволочек получилось из 42 м полотна, выполнив умножение. Решение лучше записать отдельными действиями с пояснениями. 1) 42 : 2 = 21 (раз) – столько раз в 42 м содержится по 2 м 2) 3 · 21 = 63 (н.) О т в е т: 63 наволочки получится из 42 м полотна. Для закрепления учащиеся под руководством учителя решают задачу 104. После чтения задачи сделать иллюстрацию, обозначив каждую банку, например, точкой. Ученики в тетрадях, а учитель на доске ставят в ряд 10 и 20 точек, затем рассуждают: «В этих 10 банках 16 кг меда (подчеркивают 10 точек и внизу подписывает: 16 кг). В этих 10 банках … и т. д. (подчеркивают 2 раза по 10 точек). Значит, по 16 кг столько раз, сколько в 20 содержится по 10». Далее записывается решение задачи. Ф и з к у л ь т м и н у т к а IV. Работа над пройденным материалом. 1. Решение задач. Задачу 105 на движение учащиеся решают самостоятельно (с последующей проверкой). Можно одного учащегося вызвать решать на закрытую доску. 2. Решение примеров. Выполняя задание 107, учащиеся должны составить равенства и неравенства и, посчитав, проверить, верны ли они. V. Итоги урока. Учитель. Ребята, что нового узнали на уроке? Дети. Мы учились решать новый вид задач. Учитель. Что повторяли на уроке? Дети. Мы повторили решение задач на движение, деление с остатком на 10 и 100, решали примеры. Домашнее задание: задания 106, 108, 109; тетрадь № 2, с. 23, № 8, 9. У р о к 103 Письменное деление на числа, оканчивающиеся нулями Цели: познакомить учащихся с приемом письменного деления с остатком на числа, оканчивающиеся нулями, когда в частном получается однозначное число; совершенствовать умение решать задачи на нахождение четвертого пропорционального. Ход урока I. Организационный момент. II. Устный счёт. 1. Заполните таблицу.
2. Арифметический диктант. Уменьшите 360 на 60. Уменьшите 800 в 2 раза. Увеличьте 920 на 80. Увеличьте 350 в 2 раза. Найдите разность чисел 830 и 30. Найдите сумму чисел 230 и 300. Первый множитель 140, второй 3. Найдите произведение. Делимое 91, делитель 7. Найдите частное. На сколько 90 меньше 280? На сколько 630 больше 400? Во сколько раз 810 больше 90? III. Работа над новым материалом. С целью подготовки к введению нового материала учитель должен включить данные задания. 1. Выполните деление с остатком. 167 : 10; 3 875 : 100; 65 : 20 2. Объясните по записи, данной на с. 23 (1) вверху, решение примеров 630 : 90, 5 400 : 600. Учитель. Ребята, вы научились делить на числа, оканчивающиеся нулями, когда не было остатка (он был равен нулю). При этом сначала делили на 10 или на 100, а затем результат делили на другой множитель произведения, которым заменили делитель. Этим приемом пользуются и при делении с остатком. Сегодня будем учиться письменно выполнять деление с остатком. Надо разделить 596 на 70 (запись на доске). Сколько цифр будет в частном? Дети. Одна. Учитель. Найдите частное так же, как при делении без остатка. Дети. Разделим 596 на 10 и полученное частное 59 разделим на 7, в частном будет 8. Учитель. Узнайте, сколько разделили. Дети. Умножим 70 на 8, получится 560. Учитель. Найдите остаток. Дети. Вычтем 560 из числа 596, получится 36. Учитель. Сравните остаток с делителем. Дети. 36 меньше, чем 70, значит, частное равно 8, а остаток – 36. Далее ученики читают объяснение нового материала на с. 23 (2) вверху и для закрепления решают с комментированием задания 110, 111, 112. Ф и з к у л ь т м и н у т к а IV. Работа над пройденным материалом. Задачу 113 учащиеся решают под руководством учителя. После чтения задачи дети выполняют к ней чертеж, а затем записывают решение. 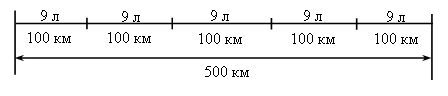 1) 500 : 100 = 5 (раз) – столько раз по 100 км укладывается в 500 км 2) 9 · 5 = 45 (л) О т в е т: 45 л бензина потребуется, чтобы проехать 500 км. Задачу 115 можно предложить учащимся решить самостоятельно (с последующей проверкой). V. Итоги урока. Учитель. Ребята, что нового узнали на уроке? Дети. Мы учились письменно делить с остатком на числа, оканчивающиеся нулями. Учитель. Что повторили на уроке? Дети. Мы закрепили решение задач. Домашнее задание: задание 116; тетрадь № 2, с. 23, № 10, 11; с. 24, № 12. У р о к 104 Прием письменного деления на числа, оканчивающиеся нулями Цели: познакомить с приемом письменного деления на двузначные разрядные числа; совершенствовать умения решать задачи на движение, на нахождение четвертого пропорционального. Ход урока I. Организационный момент. II. Устный счёт. 1. Задание «Головоломка». ? ? О ? · = 96 О + = 100 О : = 11 · 6 = 72 2. Задание «Магический квадрат».
III. Работа над новым материалом. При рассмотрении деления на числа, оканчивающиеся нулями, когда в частном получается многозначное число, следует обратиться к заданиям «Памятки». Учитель при этом должен объяснить, как выделяются неполные делимые. Учитель. Прочитайте пример. Дети. 3 240 разделить на 60. Учитель. Что надо сделать сначала? Дети. Выделить первое неполное делимое. Учитель. Здесь делитель – двузначное число, значит, первым неполным делимым будет двузначное или трехзначное число. Подходит ли двузначное число? Дети. Нет, если 32 сотни разделить на 60, получится нуль, а нуль в начале числа не пишут. Первое неполное делимое 324 десятка. Далее ученики читают объяснение по учебнику на с. 24 вверху. Для закрепления знания приема и выработки вычислительного навыка ученики решают примеры из задания 117, 118, 119 под руководством учителя, объясняя решение вслух по образцу, данному в учебнике. Ф и з к у л ь т м и н у т к а IV. Работа над пройденным материалом. После чтения задачи 120 учащиеся под руководством учителя записывают условие таблицей, после чего решают задачу самостоятельно. Можно вызвать одного учащегося на закрытую доску, а затем произвести проверку.  1) 3 600 : 60 = 60 (в.) – столько вагонов по 60 т 2) 3 600 : 90 = 40 (в.) – столько вагонов по 90 т 3) 60 – 40 = 20 (в.) О т в е т: на 20 вагонов больше. Задачу 121 дети решают самостоятельно (с последующей проверкой). V. Итог урока. Учитель. Ребята, над чем работали сегодня на уроке? Дети. Мы продолжали работать над приемом деления на числа, оканчивающиеся нулями. На уроке мы также повторили решение задач изученных видов. Домашнее задание: тетрадь № 2, с. 25, № 13–15. У р о к 105 Прием письменного деления на числа, оканчивающиеся нулями Цели: познакомить с приемом письменного деления на трехзначные числа, оканчивающиеся нулями; совершенствовать умения решать задачи и уравнения. Ход урока I. Организационный момент. II. Устный счёт. 1. Решите и найдите лишнее уравнение (вынести на доску). 54 : х = 6 28 : х = 4 72 : х = 8 45 : х = 5 27 : х = 3 7 · х = 63 18 : х = 2 2. Решить задачу. Задача 126. Дети читают задачу, рассматривают к ней чертеж и отвечают на вопросы. 3. Сравните выражения. Задача 127 (вынести на доску). 586 · 10 · 7 … 586 · 70 1 200 : 20 … 1 200 : 100 : 2 36 · 800 … 36 · 9 · 100 900 : 10 : 5 … 900 : 50 III. Работа над новым материалом. В качестве подготовки включить для устного решения примеры: 320 : 100, 507 : 100, 1 250 : 100, 724 : 200, 1 350 : 400. При решении двух последних примеров ученики дают краткое объяснение. Например: «Чтобы 724 разделить на 200, достаточно 7 разделить на 2, в частном получится 3; разделили 600, остаток 124». Опираясь на объяснение, данное на предыдущем уроке, и «Памятку» в учебнике, ученики могут сами объяснить приемы деления по записям, представленным в задании 122: «Первое неполное делимое 4 980 десятков. В частном будет двузначное число. Узнаем, сколько десятков будет в частном. Разделим 4 980 на 100, полученный результат 49 разделим на 6, получим 8. Узнаем, сколько десятков разделили. Умножим 600 на 8, получится 4 800. Узнаем, сколько десятков осталось разделить. Вычтем 4 800 из 4 980, получится 180 … и т. д.» Так же ученики объясняют решение второго примера. Примеры из заданий 123, 124 учащиеся решают с объяснением, выполняя запись в столбик на доске и в тетрадях. |
