поурочные планы математика 4 класс Школа России. поурочные планы математика. Основные требования к знаниям, умениям и навыкам учащихся к концу 4 класса учащиеся должны знать
 Скачать 2.41 Mb. Скачать 2.41 Mb.
|
|
III. Работа над новым материалом. Учитель. Ребята, в жизни часто встречаются такие выражения, как «средний заработок», «средняя температура» и др. Сегодня мы с вами разберем на примере задач, что значит понятие «средний», как его определяют. Откройте учебник на с. 90. Прочитайте первую задачу во вводной статье. Дети читают. Учитель. А теперь по объяснению, которое там дается, давайте запишем с вами решение. (182 + 185 + 173) : 3 = 180 (шагов) Учитель. Прочитайте вторую задачу. Как запишем решение? (3 м + 2 м 80 см + 3 м 20 см +3 м 40 см) : 4 = 3 м 10 см Учитель. Молодцы. Решаем задачу 449. (63 + 62 + 70) : 3 = 65 (г) Ф и з к у л ь т м и н у т к а IV. Работа над пройденным материалом. 1. Решение уравнений. В задании 450 дети должны сначала составить уравнения, а потом их решить. Задания можно выполнять с комментированием у доски, вызывая по одному ученику. 2. Решение задач. Задачу 451 учащиеся решают самостоятельно (с последующей проверкой). 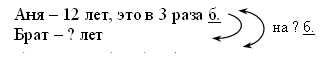 1) 12 : 3 = 4 (года) – брат 2) 12 – 4 = 8 (лет) О т в е т: на 8 лет Аня старше брата. V. Итоги урока. Учитель. Ребята, что нового узнали на уроке? Дети. Мы сегодня решали задачи с новым понятием «средний». Учитель. Что повторяли на уроке? Дети. Мы повторяли решение уравнений, решали задачу косвенного вида и чертили потом отрезки. Домашнее задание: задание 452; тетрадь № 1, с. 62, № 39–42 У р о к 74 Решение задач на нахождение среднего значения Цели: познакомить учащихся с решением более трудных задач на нахождение среднего значения; совершенствовать вычислительные навыки и умения решать уравнения. Ход урока I. Организационный момент. II. Устный счёт. 1. Задание 455 на с. 91. Дети читают задачу и составляют по ней буквенные выражения. 2. Найдите ошибки и вычислите правильно (можно вынести на доску). 39 : 6 = 5 (ост. 9) 65 : 9 = 7 (ост. 3) 60 : 12 = 4 (ост. 12) 24 : 36 = 0 (ост. 12) 3. Переведите (можно вынести на доску). 23 м 6 см = … см 2 355 кг = … т… кг 9 ч 6 с = … с 62 335 = … т … кг 2 ч 45 мин = … мин 584 мм = … см … мм III. Работа над новым материалом. Учитель. Ребята, сегодня на уроке мы продолжим работу над задачами на нахождение среднего значения. Только сегодня разберем задачи уже посложнее. Откройте учебник на с. 91. Прочитайте первую задачу в самом верху страницы и объяснение к ней. Давайте запишем решение. Дети читают задачу и записывают решение. 1) 25 · 3 = 75 (л) – за 3 дня 2) 30 · 2 = 60 (л) – за 2 дня 3) 75 + 60 = 135 (л) – всего 4) 3 + 2 = 5 (д.) – всего 5) 135 : 5 = 27 (л) О т в е т: 27 л молока расходовали в среднем. После этого дети читают и решают с комментированием вторую задачу. 1) 30 · 4 = 120 (д.) – за первые 4 ч 2) 20 · 4 = 80 (д.) – за вторые 4 ч 3) 4 + 4 = 8 (ч) – всего работал 4) 120 + 80 = 200 (д.) – всего сделал за 8 ч 5) 200 : 8 = 25 (д.) О т в е т: 25 деталей в час в среднем изготавливал рабочий. Для закрепления знаний учащиеся под руководством учителя решают задачу 454. 1) 5 · 2 = 10 (км) – за первые 2 ч 2) 4 · 2 = 8 (км) – за вторые 2 ч 3) 3 · 2 = 6 (км) – за третьи 2 ч 4) 10 + 8 + 6 = 24 (км) – прошли всего 5) 2 + 2 + 2 = 6 (ч) – всего были в пути 6) 24 : 6 = 8 (км) О т в е т:8 км в час в среднем проходили туристы. Ф и з к у л ь т м и н у т к а IV. Работа над пройденным материалом. Задания 456 и 457 учащиеся решают самостоятельно. V. Итоги урока. Учитель. Ребята, над чем работали сегодня на уроке? Дети. Сегодня мы продолжали решать задачи на нахождение среднего значения. Учитель. Что повторяли на уроке? Дети. Мы составляли и решали уравнения, а также повторяли нахождение значения выражения с переменной. Домашнее задание: задания 458, 459. У р о к 75 Скорость. Единицы скорости Цели: познакомить детей со скоростью равномерного движения и с решением простых задач на нахождение скорости по известным расстоянию и времени движения; совершенствовать вычислительные навыки. Ход урока I. Организационный момент. II. Устный счёт. 1. Восстановите цепочку вычислений. 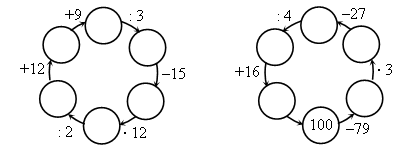 2. Арифметический диктант. Найдите частное чисел 420 и 6. Какое число меньше 720 на 100? Какое число надо увеличить на 8, чтобы получить 64? Запишите число, которое больше 20 в 5 раз. На сколько надо разделить 560, чтобы получить 80? К какому числу надо прибавить 100, чтобы получить 360? Первый множитель 42, второй 2. Чему равно произведение? Во сколько раз 70 больше 2? Уменьшаемое 360, вычитаемое 60. Чему равна разность? Из чисел 625, 506, 650, 605, 526, 256, 560 выпишите те, у которых 6 единиц I разряда и 5 единиц III разряда (числа записываются на доске). III. Работа над новым материалом. Учитель. Ребята, вы уже знаете такие величины, как время и расстояние, а также единицы их измерения. А сегодня на уроке мы познакомимся с новой величиной, которая называется «скорость»; узнаем, как связаны между собой скорость, время и расстояние. Ребята, откройте учебник на с. 92 и прочитайте решения задач, которые даны вверху. Дети открывают учебник, читают задачи и к ним решения. После этого дети устно решают задачу 460, а затем под руководством учителя выполняют задачу 461 (1, 2). З а д а ч а 461 (1). 1-й час – 75 км 2-й час – 60 км 3-й час – 75 км Сред. скорость – ? (75 + 60 + 75) : 3 = 70 (км/ч) О т в е т: средняя скорость поезда 70 км/ч. Учитель. Ребята, задачу 461 (2) мы с вами оформим в таблицу. Для краткой записи скорость обозначается буквой , время – t, расстояние – S.
Учитель. Сколько часов был в пути поезд? Дети. 3 ч. Учитель. Это – время движения поезда. Запишем название этой величины и ее значение в таблице. Сколько всего километров проехал поезд? Дети. 120 км. Учитель. Это расстояние, пройденное поездом. Запишем в таблице. Учитель. Что сказано в задаче о том, какое расстояние проходил поезд в течение каждого часа? Дети. Одинаковое. Учитель. Что надо узнать? Дети. Скорость. Учитель. Подумайте, как можно найти скорость? Дети. Надо расстояние 120 км разделить на время – 3 ч. Учитель. Запишем решение и ответ. 120 : 3 = 40 (км/ч) О т в е т: скорость поезда 40 км/ч. Учитель. Ребята, так как же, зная время и расстояние, можно найти скорость? Дети. Чтобы найти скорость, надо расстояние разделить на время. Для закрепления представлений о скорости ученики под руководством учителя выполняют задачу 464. 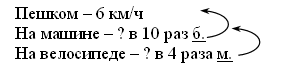 1) 6 · 10 = 60 (км/ч) – на машине 2) 60 : 4 = 15 (км/ч) О т в е т: скорость на велосипеде 15 км/ч. Ф и з к у л ь т м и н у т к а IV. Работа над пройденным материалом. Для самостоятельной работы учащимся можно предложить решить примеры из задания 462, 465. V. Итоги урока. Учитель. Ребята, что нового узнали на уроке? Дети. Мы познакомились с новой величиной – скоростью. Узнали, как она связана с временем и расстоянием, учились решать с ней задачи. Учитель. Что повторили на уроке? Дети. Мы повторили решение примеров. Домашнее задание: задание 463; тетрадь № 1, с. 63, № 1–3. У р о к 76 Взаимосвязь между скоростью, временем и расстоянием Цели: познакомить с решением задач на нахождение расстояния по известным скорости и времени движения; совершенствовать вычислительные навыки и умения решать уравнения. Ход урока I. Организационный момент. II. Устный счёт. 1. Выполните действия: 39 : 13 + 28 · 1 37 : 37 + 14 · 5 65 – 48 : (81 : 27) (64 + 29) : 3 2. Сравните: 87 см … 8 дм 7 см 6 км 300 м … 6 км 30 м 9 дм 2 см … 9 дм 20 мм 6 м 3 см … 6 м 3 дм 7 т 420 кг … 7 т 42 ц 3. Найдите: Скорость космического корабля, если он пролетел 56 км за 8 с. Скорость улитки, если она проползла 35 м за 7 ч. Скорость плота на реке, если он за 4 ч проплыл 16 км. Скорость велосипедиста, если он проехал 36 км за 2 ч. III. Работа над новым материалом. Учитель. Ребята, сегодня мы продолжаем учиться решать задачи с величинами: скорость, время, расстояние. Откройте учебник на с. 9 и прочитайте задачу 466. Прочитав задачу, учащиеся называют величины, данные в условии (скорость, время, расстояние), и записывают их в таблице. Затем называют и записывают в таблице значения данных и искомых величин.
Учитель. С какой скоростью двигалась черепаха? Дети. 5 м в минуту. Учитель. Что это значит? Дети. В каждую минуту черепаха проползала по 5 метров. Учитель. А сколько она была в пути? Дети. 3 минуты. Учитель. Чтобы вам было легче решить задачу, сделаем еще к ней чертеж. 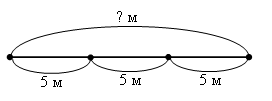 Учитель. Что надо узнать? Дети.Какое расстояние черепаха прошла. Учитель. Как это можно узнать? Дети. Надо 5 умножить на 3, получится 15. Учитель. Запишем решение и ответ. 5 · 3 = 15 (м) О т в е т:15 метров прошла черепаха. Аналогично учитель с учащимися разбирают вторую задачу.
100 · 10 = 1 000 (м) О т в е т: 1 000 м прошел слон за 10 минут. После решения второй задачи учащиеся должны сделать вывод. Учитель. Как найти расстояние, если известны скорость и время движения? Дети. Надо скорость умножить на время. Для закрепления умения решать подобные задачи учащиеся выполняют с комментированием у доски задачи 467 и 468. З а д а н и е 467.
30 : 6 = 5 (м/с) О т в е т: скорость Тани 5 м/с. З а д а н и е 468.
1) 60 · 3 = 180 (км) – проехал за 3 ч 2) 70 · 2 = 140 (км) – проехал за 2 ч 3) 180 + 140 = 320 (км) – всего 4) 3 + 2 = 5 (ч) - всего 5) 320 : 5= 65 (км/ч) – средняя скорость О т в е т: 320 км проехал всего, 65 км/ч – средняя скорость. Ф и з к у л ь т м и н у т к а IV. Работа над пройденным материалом. Выполняя задание 469, ученики сначала объясняют, в каком из уравнений каждой пары значение х будет больше, а потом проверяют вычислением. V. Итоги урока. Учитель.Ребята, над чем работали сегодня на уроке? Дети. Мы продолжали учиться решать задачи на движение, повторили решение уравнений. Домашнее задание: задание 470; тетрадь № 1, с. 63, № 4–6. У р о к 77 Тема: Нахождение времени движения по известным расстоянию и скорости Цели: познакомить с решением задач на нахождение времени движения по известным расстоянию и скорости; совершенствовать вычислительные навыки и умения выполнять действия с величинами; закрепить знание отношений единиц длины, массы, времени. Ход урока I. Организационный момент. II. Устный счёт. 1. Расшифруйте имя среднеазиатского математика и поэта, предложившего одну из самых интересных систем календарей.
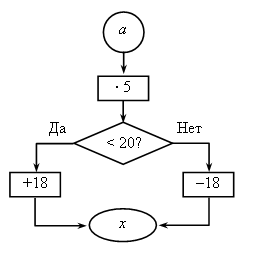 2. Заполните таблицу. Перед заполнением таблицы дети сначала говорят, какие величины известны, а какую величину надо найти. Потом говорят правило, как найти неизвестную величину, а затем решение и ответ.
|
