поурочные планы математика 4 класс Школа России. поурочные планы математика. Основные требования к знаниям, умениям и навыкам учащихся к концу 4 класса учащиеся должны знать
 Скачать 2.41 Mb. Скачать 2.41 Mb.
|
|
V. Итоги урока. Учитель. Ребята, что нового узнали на уроке? Дети. На уроке мы учились чертить прямоугольник на нелинованной бумаге с помощью циркуля и линейки. Учитель. Что повторяли на уроке? Дети. Мы повторяли на уроке решение задач и примеров. Домашнее задание: задание 31; тетрадь № 2, с. 6, № 10–12. У р о к 86 Умножение числа на произведение Цели: познакомить учащихся со свойством умножения числа на произведение; учить применять это свойство при решении задач и примеров; совершенствовать вычислительные навыки. Ход урока I. Организационный момент. II. Устный счёт. 1. Цепочка. 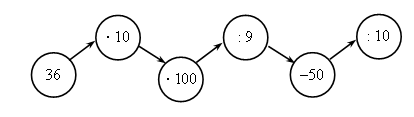 2. Арифметический ребус. 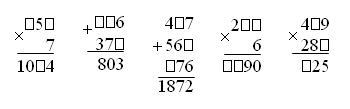 III. Работа над новым материалом. Ознакомление с разными способами умножения числа на произведение можно провести в опоре на рисунок и записи данных на с. 8 учебника. Ученики рассматривают рисунок, где изображены пятирублевые монеты. Дети говорят, сколько монет в ряду, считая слева направо, и сколько таких рядов; сколько монет в ряду, считая сверху вниз, и сколько таких рядов. Учитель. Справа от рисунка записано, как по-разному можно найти, сколько всего рублей составляют эти монеты. Прочитайте первое выражение и объясните, как этим способом нашли, сколько всего рублей. Дети. Здесь число 5 умножили на произведение чисел 4 и 2. Когда 4 умножили на 2, то узнали, что в двух рядах 8 монет, каждая монета по 5 рублей, умножив 5 на 8, узнали, сколько всего рублей. Затем дети объясняют, как узнали другими способами, сколько всего рублей. Учитель. Теперь сравните выражения и скажите, как получили второе выражение из первого. Дети. Умножили число 5 на 4 (на первый множитель) и результат 20 умножили на 2 (на второй множитель), получили тоже 40. Учитель. Скажите, как получили третье выражение из первого? Дети. Умножили число 5 на 2 (на второй множитель) и результат 10 умножили на 4 (на первый множитель), получилось тоже 40. Учитель. Как видите, можно по-разному умножить число 5 на произведение чисел 4 и 2, получая одинаковые результаты. Далее по записям в учебнике (задание 35) ученики рассказывают, как умножили разными способами число 6 на произведение чисел 3 и 4. После этого учитель спрашивает, как же можно умножить число на произведение. Ученики называют три способа умножения числа на произведение: 1) можно найти произведение и умножить число на полученный результат; 2) можно умножить число на первый множитель и полученный результат умножить на второй множитель; 3) можно умножить число на второй множитель и полученный результат умножить на первый множитель. Для закрепления полученных знаний учащиеся выполняют задание 36, где рассказывают, как можно по-разному умножить число 7 на произведение чисел 2 и 5 и число 4 на произведение чисел 5 и 3. При выполнении задания 37 учащиеся устно называют все способы и, сравнивая их, выбирают наиболее удобный. Пример объяснения: 12 · (5 · 7). 1) Можно 5 умножить на 7, получится 35, и 12 умножить на 35 – это устно выполнить трудно. 2) Можно 12 умножить на 5, получится 60, и 60 умножить на 7, получится 420. 3) Можно 12 умножить на 7, получится 84, и 84 умножить на 5 – это труднее. Самый удобный второй способ, запишем его. Ф и з к у л ь т м и н у т к а IV. Работа над пройденным материалом. 1. Решение задач. Задачу 38 учащиеся решают под руководством учителя. Дети читают задачу, записывают краткое условие: 1 корова – 14 л в сут. 10 коров – ? л за 7 сут. Учитель предлагает записать решение задачи двумя способами. I способ: 1) 14 · 10 = 140 ( л) – 10 коров за 1 сутки 2) 140 · 7 = 980 (л) II способ: 1) 14 · 7 = 98 (л) – 1 корова за 7 суток 2) 98 · 10 = 980 (л) О т в е т: 980 л молока получают от 10 коров за 7 суток. 2. Решение примеров. Задание 40 учащиеся могут решить самостоятельно. V. Итоги урока. Учитель. Ребята, что нового узнали сегодня на уроке? Дети. Мы узнали, как можно по-разному умножать число на произведение, использовали полученные знания при решении разными способами примеров и задач. Домашнее задание: задание 39; тетрадь № 2, с. 9, № 20–23. У р о к 87 письменное умножение на числа, оканчивающиеся нулями Цели: познакомить с письменным приемом умножения на числа, оканчивающиеся нулями; повторить решение задач с величинами: скорость, время, расстояние; закрепить решение уравнений и перевод единиц площади. Ход урока I. Организационный момент. II. Устный счёт. 1. Задание 44 на с. 9. Учащиеся объясняют, что показывают заданные к задаче выражения. 2. Выразите в квадратных сантиметрах. 6 дм2 600 мм2 2 дм2 35 см2 1 500 мм2 3. Заполните таблицу. Перед заполнением таблицы дети вспоминают взаимосвязь между величинами: скорость, время, расстояние.
III. Работа над новым материалом. Ознакомление с приемом письменного умножения на числа, оканчивающиеся нулями, можно провести так: предложить ученикам объяснить решение примера, записанного учителем на доске, например: 847 · 60 = 847 · (6 · 10) = 847 · 6 · 10 = 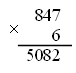 Объяснив, как выполнены операции, ученики затрудняются вычислить устно произведение 847 · 6. Учитель объясняет: «Если устно вычислить трудно, то решение выполняют письменно. Умножают 847 на 6, и полученный результат умножают на 10. Умножьте 847 на 6». Дети умножают. Учитель. Умножьте полученный результат 5 082 на 10. Для этого достаточно к числу 5 082 приписать справа один ноль, получится 50 820. Теперь ученики смогут сами объяснить решение примеров 243 ·20 и 532 · 300, которые даны в учебнике на с. 9 вверху, сначала по развернутой записи в строчку, а затем по записи в столбик. Для закрепления знания приема ученики выполняют задание 41, часть примеров они решают под руководством учителя, а остальные – самостоятельно. Ф и з к у л ь т м и н у т к а IV. Работа над пройденным материалом. 1. Решение задач. Задачу 42 учащиеся решают с комментированием у доски, записывая решение в виде отдельных действий столбиком. 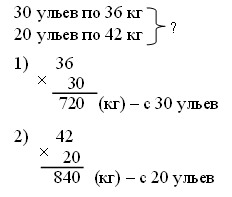 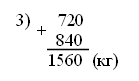 О т в е т:1560 кг всего. Задачу 43 учащиеся решают самостоятельно (с последующей проверкой), условие записывают в таблицу.  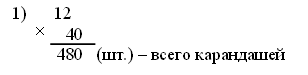 2) 560 – 480 = 80 (шт.) – всего фломастеров 3) 80 : 10 = 8 (шт.) О т в е т: 8 фломастеров в одной коробке. 2. Решение уравнений. Задание 45 учащиеся могут решить самостоятельно. V. Итоги урока. Учитель. Ребята, что нового узнали на уроке? Дети. Мы познакомились с письменным приемом умножения на числа, оканчивающиеся нулями. Учитель. Что закрепляли на уроке? Дети. Мы закрепляли решение задач и уравнений. Домашнее задание: задание 47; тетрадь № 2, с. 10, № 1–3. У р о к 88 Письменное умножение на числа, оканчивающиеся нулями Цели: совершенствовать навыки умножения на числа, оканчивающиеся нулями, закрепить умение решать задачи. Ход урока I. Организационный момент. II. Устный счёт. 1. Решите примеры. 20 · 8 : 40 650 : 5 · 3 : 10 75 : 3 · 2 – 18 280 · 2 : 80 · 12 800 : 100 · 9 : 3 100 – 72 : 9 · 11 600 : 10 · 3 : 18 15 · (16 – 9) : 3 2. Решение задач. З а д а ч а 53 (1, 2). Дети читают задачи, рассматривают чертеж и отвечают на вопросы. 3. Арифметические ребусы. 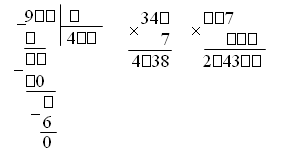 III. Закрепление пройденного материала. 1. Решение примеров. Задание 48 учащиеся решают с комментированием у доски. Задание 49 детям можно предложить решить с комментированием только первый столбик, а остальные два столбика учащиеся решают самостоятельно. Ф и з к у л ь т м и н у т к а 2. Решение задач. После чтения задачи 50 учащиеся записывают краткое условие, составляют план решения, а затем решают самостоятельно, записывая решение в виде отдельных действий. Можно вызвать одного учащегося решать на закрытую доску, а потом произвести проверку. 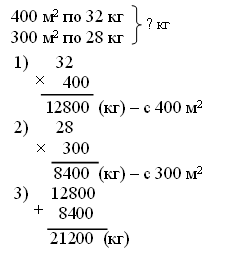 О т в е т: 21 200 кг всего. Задачу 51 учащиеся решают самостоятельно. IV. Итоги урока. Учитель. Ребята, что закрепляли на уроке? Дети. Мы закрепляли письменный прием умножения и умение решать задачи. Домашнее задание: задание 52; тетрадь № 2, с. 11, № 4, 5; с. 12, № 6–9. У р о к 89 Письменное умножение двух многозначных чисел, оканчивающихся нулями Цели: познакомить с приемом письменного умножения для случаев, когда оба множителя оканчиваются нулями; закрепить умение решать задачи и уравнения; совершенствовать знание отношений единиц площади и умение находить значения буквенных выражений. Ход урока I. Организационный момент. II. Устный счёт. 1. Решение задач. Задачу 58 учащиеся читают и устно отвечают на ее вопрос. 2. Переведите. Задание 61 (можно вынести на доску). 8 см2 25 м2 = … мм2 30 а = … м2 2 400 а = … га 9 дм2 18 см2 = … см2 85 га = …а 3 800 м2 = … а 3. Геометрический материал. Задание 54 на с. 10 (можно вынести на доску). Рассмотрите чертеж. Сколько на нем всего треугольников? Назовите среди этих треугольников тупоугольные, прямоугольные и остроугольные. 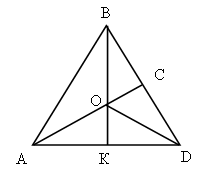 III. Работа над новым материалом. Сначала учителю надо ввести устный прием умножения для этих случаев. Учитель. Вычислим устно произведение чисел 70 и 30. Умножу 70 на 3, для этого 7 десятков умножу на 3, получится 21 десяток, или 210; умножу теперь 210 на 10, получится 2 100. Возможно, что после этого дети сами смогут «открыть» способ, если нет, то учитель подводит итог: «Сначала умножили 7 на 3, то есть умножили числа, не обращая внимания на нули, а затем к полученному произведению приписали столько нулей, сколько их записано в конце обоих множителей вместе, – два нуля». После этого по записям, данным в учебнике на с. 11 вверху, ученики объясняют прием устного умножения чисел, оканчивающихся нулями. Для закрепления полученных знаний можно решить устно задание 56 (1-й и 2-й столбики). При этом дети каждый раз замечают, что сначала умножили числа, не обращая внимания на нули, которыми оканчиваются их записи, а затем к произведению приписали столько нулей, сколько их записано в конце обоих множителей вместе. Далее учитель объясняет прием письменного умножения чисел, оканчивающихся нулями. 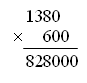 Учитель. Если трудно вычислять устно произведения чисел, оканчивающихся нулями, то умножение выполняют письменно. Например, надо умножить 1 380 на 600. Подпишем второй множитель под первым так, чтобы его цифра, отличная от нуля, стояла под первой цифрой справа, отличной от нуля первого множителя. Тогда нули обоих множителей будут записаны справа. Будем умножать 138 дес. на 600. Как это сделать? Дети. Умножить 138 на 6 и результат умножить на 100. Учитель. Умножим на 6: шестью восемь – 48, 8 пишем, 4 запоминаем; трижды шесть – 18, да 4, это 22; 2 пишем, 2 запоминаем; 1 умножить на 6, получится 6, да 2, всего 8. Что получили? Дети. 828 десятков. Учитель. Умножаем их на 100. Сколько получится? Дети. 82 800 десятков. Учитель. Выразите их в единицах. Дети. 828 000. Затем ученики объясняют по записям в учебнике на с. 11 вверху, как выполнено письменное умножение. Для закрепления приема письменного умножения учащиеся решают с комментированием задание 55. Примеры из задания 56 (3-й столбик) учащиеся решают самостоятельно. Ф и з к у л ь т м и н у т к а IV. Работа над пройденным материалом. 1. Решение задач. После чтения задачи 57 дети ставят к ней вопрос: «Найдите скорость второго теплохода». Затем под руководством учителя делают чертеж. 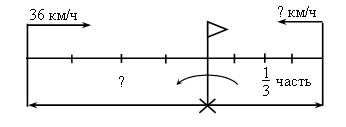 Затем дети вспоминают формулы нахождения расстояния и скорости: S = : t, = S : t. Решение задачи выполняют самостоятельно, когда коллективно составят план решения. 1) 36 · 4 = 144 (км) – прошел первый теплоход 2) 144 : 3 = 48 (км) – прошел второй теплоход 3) 48 : 4 = 12 (км/ч) О т в е т: 12 км/ч – скорость второго теплохода. 2. Решение уравнений. Задание 60, где надо записать и решить уравнения, дети выполняют самостоятельно. V. Итоги урока. Учитель. Ребята, что нового узнали на уроке? Дети. Мы учились умножать два числа, оканчивающихся нулями. Учитель. Что повторили на уроке? Дети. Мы повторили решение задач на движение и решение уравнений. Домашнее задание: задание 59; тетрадь № 2, с. 13, № 10–12. У р о к 90 Решение задач на встречное движение Цели: познакомить учащихся с решением задач на встречное движение; закрепить умение решать задачи на нахождение среднего значения; совершенствовать вычислительные навыки. Ход урока I. Организационный момент. II. Устный счёт. 1.Задание «Цепочка». 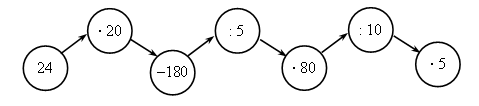 2. Задание 64 (можно вынести на доску). 6 · 4 · 5 – 100 2 · 7 · 25 + 150 50 · 9 · 2 – 80 19 · 9 · 4 – 540 III. Работа над новым материалом. Учитель выполняет заранее на доске такой же чертеж, как в задаче 62 (1). 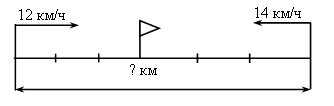 Учитель. Прочитайте задачу. Как движутся лыжники? Дети. Навстречу друг другу. Учитель. Как это показано на чертеже? Дети. Стрелками. Учитель. Что известно о времени их выхода? Дети. Они вышли одновременно. Учитель. Как обозначено место встречи? Дети. Флажком. Учитель. Сколько времени будет идти до встречи каждый лыжник? Дети. Каждый будет идти 3 ч. Учитель. Известны ли скорости лыжников? Дети. Первый идет со скоростью 12 км/ч, а второй – 14 км/ч. Учитель. Который из лыжников пройдет до встречи большее расстояние? Почему? Дети. Второй лыжник. Он шел с большей скоростью, а времени затратил столько же, сколько первый. Учитель. Что требуется узнать? Дети. Расстояние между поселками. Учитель. Как видим по чертежу, часть этого расстояния прошел первый лыжник, а другую часть – второй лыжник. Покажите эти части на чертеже. Как же узнать расстояние между поселками? |
