поурочные планы математика 4 класс Школа России. поурочные планы математика. Основные требования к знаниям, умениям и навыкам учащихся к концу 4 класса учащиеся должны знать
 Скачать 2.41 Mb. Скачать 2.41 Mb.
|
|
Дети. Сначала узнаем расстояние, которое прошел первый лыжник до встречи, затем – расстояние, которое прошел второй лыжник до встречи, после этого можно будет узнать все расстояние. Учитель. Запишем решение задачи. На доске и в тетрадях появляется запись. 1) 12 · 3 = 36 (км) – прошел первый лыжник 2) 14 · 3 = 42 (км) – прошел второй лыжник 3) 36 + 42 = 78 (км) Учитель. Ребята, эту задачу можно решить другим способом. Для разбора решения этой задачи другим способом учитель может провести объяснение, вызвав к чертежу двух учеников. Учитель. Вы будете лыжниками. Покажите указкой, откуда вы начали движение. Вы начали движение одновременно и двигались 1 час. Сколько км прошел за это время первый лыжник? Дети. 12 км. Учитель. Второй лыжник? Дети. 14 км. Учитель. Отметим точками эти расстояния и подпишем под ними «12 км» и «14 км». На сколько километров лыжники сблизились за 1 час? Дети. На 26 км. Учитель. Прошел второй час. На сколько км еще сблизились лыжники? Дети. Еще на 26 км. Учитель. Подпишем «12 км» и «14 км». Прошел третий час. На сколько километров еще сблизились лыжники? Дети. На 26 км. Учитель. Подпишем «12 км» и «14 км». Встретились лыжники? Дети. Да. Учитель. Кто догадался, как по-другому решить задачу? Ученики рассказывают план решения. Решение записывают отдельными действиями. II способ: 1) 12 + 14 = 26 (км/ч) – скорость сближения 2) 26 · 3 = 78 (км) О т в е т: 78 км между поселками. Аналогично рассматриваются решения двух других задач из этого номера, причем вторая задача решается одним способом, а третья – двумя. Приведем решения этих задач. З а д а ч а 62 (2). 1) 12 + 14 = 26 (км/ч) – скорость сближения 2) 78 : 26 = 3 (ч) О т в е т: через 3 часа произошла встреча. З а д а ч а 62 (3). I способ: 1) 12 · 3 = 36 (км) – прошел первый лыжник 2) 78 – 36 = 42 (км) – прошел второй лыжник 3) 42 : 3 = 14 (км/ч) II способ: 1) 78 : 3 = 26 (км/ч) – скорость сближения 2) 26 – 12 = 14 (км/ч) О т в е т: скорость второго лыжника – 14 км/ч. Ф и з к у л ь т м и н у т к а IV. Работа над пройденным материалом. Решить задание 65 можно предложить учащимся самостоятельно. V. Итоги урока. Учитель. Ребята, что нового узнали на уроке? Дети. Мы учились решать задачи на встречное движение. Домашнее задание: тетрадь № 2, с. 14, № 13–5; с. 15, № 16–19. У р о к 91 Перестановка и группировка множителей Цели: познакомить учащихся с приемом перестановки и группировки множителей; закрепить умение решать задачи на встречное движение; совершенствовать вычислительные навыки. Ход урока I. Организационный момент. II. Устный счёт. 1. Решите цепочки примеров.  2. Найдите закономерность и продолжите ряд чисел. 0, 36, 72, 108, …, …, … . 5, 6, 8, 11, 15, 20, …, …, … . 1, 3, 7, 13, 21, 31, …, …, … . 3. Ответьте на вопросы: Сколько сантиметров в пятой части метра? Сколько граммов в четвертой части килограмма? Сколько минут в шестой части часа? Сколько сантиметров в 500 м? Сколько центнеров в 400 т? Во сколько раз 1 м больше, чем 1 дм? III. Работа над новым материалом. Дети вспоминают свойства умножения по таблице на с. 101 (1, 2). Затем объясняют, почему верны равенства на с. 13 вверху. В результате делается вывод: множители можно переставлять и группировать любыми способами. Этот вывод дети читают по учебнику. Для закрепления знания приема перестановки и группировки множителей учащиеся выполняют устно задания 66, 67. Ф и з к у л ь т м и н у т к а IV. Работа над пройденным материалом. 1. Решение задач. Задачу 68 учащиеся решают с комментированием у доски. После чтения задачи дети делают чертеж, объясняют по чертежу, что известно и что надо узнать, после чего записывают решение по действиям. Учитель может предложить решить эту задачу двумя способами. 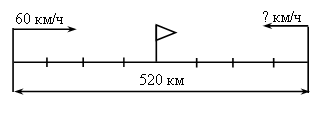 I способ: 1) 60 · 4 = 240 (км) – прошел первый поезд 2) 520 – 240 = 280 (км) – прошел второй поезд 3) 280 : 4 = 70 (км/ч) II способ: 1) 520 : 4 = 130 (км/ч) – скорость сближения 2) 130 – 60 = 70 (км/ч) О т в е т: скорость второго поезда 70 км/ч. Аналогично под руководством учителя разбирается задача 69. 2. Решение примеров. Задание 72 учащиеся решают самостоятельно (с последующей проверкой). V. Итоги урока. Учитель. Ребята, над чем работали сегодня на уроке? Дети. Мы повторили перестановку и группировку множителей, закрепили решение задач на встречное движение, вспомнили решение уравнений. Домашнее задание: задание 70; тетрадь № 2, с. 16, № 20, 21; с. 17, № 22. У р о к 92 Умножение чисел, оканчивающихся нулями Цели: продолжить работу по формированию у учащихся вычислительных навыков, умений решать задачи и записывать выражения. Ход урока I. Организационный момент. II. Устный счёт. 1. Вычислите цепочки примеров. 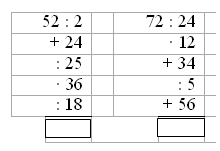 2. Сравните, на с. 15 задание 3 (можно вынести на доску). 18 · 40 … 18 · 4 · 10 36 · 5 · 10 … 36 · 15 72 · 14 … 72 · 10 · 4 98 · 21 … 98 · 3 · 7 3. Задача 75. Дети читают задачу и решают устно. III. Закрепление пройденного материала. 1. Решение задач. Задачу 74 учащиеся решают самостоятельно после того, как выполнен чертеж на доске и составлен план решения. Учитель может попросить решить эту задачу двумя способами. 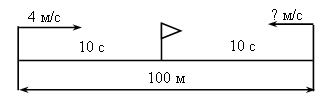 I способ: 1) 4 · 10 = 40 (м) – пробежал первый мальчик 2) 100 – 40 = 60 (м) – пробежал второй мальчик 3) 60 : 10 = 6 (м/с) II способ: 1) 100 : 10 = 10 (м/с) – скорость сближения 2) 10 – 4 = 6 (м/с) О т в е т: скорость второго мальчика 6 м/с. Задачу 76 учитель разбирает вместе с учащимися. После чтения задачи один ученик идет к доске и выполняет чертеж. Учитель. Ребята, посмотрите внимательно на чертеж и скажите, на сколько равных частей мы разбили весь отрезок? Дети. На 6 равных частей. Учитель. Как узнать чему равна длина Дети. Надо длину всего отрезка 90 мм разделить на 6. Получится 15. Учитель. А как найти длину Дети. Надо 90 разделить на 6 и умножить на 5. После этого дети выполняют в тетради чертеж и записывают решение. 1) 90 : 6 = 15 (мм) – 2) 90 : 6 · 5 = 75 (мм) – О т в е т: Задачу 77 учащиеся решают самостоятельно (с последующей проверкой). 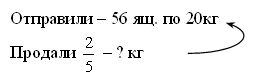 Осталось – ? кг 1) 20 · 56 = 1120 (кг) – отправили 2) 1120 : 5 · 2 = 448 (кг) – продали 3) 1120 – 448 = 672 (кг) О т в е т: 672 кг осталось. Ф и з к у л ь т м и н у т к а 2. Решение примеров. Задания 73 и 80 учащиеся решают самостоятельно. IV. Итог урока. Учитель. Ребята, что закрепляли на уроке? Дети. На уроке мы закрепляли решение задач двумя способами, вспоминали деление с остатком, выполняли задание с долями. Домашнее задание: задания 79, 81; тетрадь № 2, с. 17, № 23–24; с. 18, № 25. У р о к 93 Контрольная работа Цели: проверить понимание учащимися зависимости между скоростью, временем и расстоянием при равномерном движении; проверить также умение выполнять умножение и деление многозначного числа на однозначное число, переводить единицы длины, массы, времени. Ход урока I в а р и а н т 1. Решите задачу. Туристы ехали на автобусе 3 часа со скоростью 60 км/ч и шли пешком 5 часов со скоростью 6 км/ч. На сколько больше их путь на автобусе, чем пешком? 2. Решите задачу. Поезд прошел 250 км со скоростью 50 км/ч. За то же время автомобиль проехал 300 км. Какова скорость автомобиля? 3. Решите примеры столбиком. 4 123 · 2 1 263 : 3 603 · 8 1 635 : 5 1 200 · 4 5 910 : 3 4. Переведите. 3 ч = … мин 1 мин 25 с = … с 25 км = … м 16 дм = … м … дм 8 т = … кг 2 500 г = … кг … г II в а р и а н т 1. Решите задачу. Теплоход шел по озеру 2 часа со скоростью 42 км/ч, затем 3 часа вверх по реке со скоростью 40 км/ч. Какой путь прошел теплоход? 2. Решите задачу. Велосипедист проехал 30 км со скоростью 10 км/ч. За это же время пешеход прошел 12 км. С какой скоростью шел пешеход? 3. Решите примеры столбиком. 1 236 · 4 2 448 : 3 708 · 9 7 528 : 2 3 600 · 5 8 910 : 9 4. Переведите. 300 см = … м 5 т 200 кг = … кг 25 000 мм = … м 180 дм = … м … дм 2 мин = … с 1 350 см = … м … см У р о к 94 Работа над ошибками. Закрепление пройденного Цели: дать анализ контрольной работы; закрепить пройденный материал. Ход урока На этом уроке учитель вместе с детьми анализирует результаты прошедшей контрольной работы, помогает выполнить учащимся работу над ошибками в тех заданиях, где они были допущены, подбирает похожие задания, чтобы отработать необходимые навыки и умения. Учитель может предложить задания такого вида: 1. Решить задачи. Журавль летел 3 ч со скоростью 50 км/ч и еще 5 ч со скоростью 48 км/ч. Какое расстояние пролетел журавль? Моторная лодка прошла путь 50 км, двигаясь со скоростью 25 км/ч. За это же время байдарка прошла 10 км. С какой скоростью шла байдарка? 2. Решите примеры. 1 309 · 8 4 085 : 5 460 · 5 2 163 : 7 3 681 · 7 4 320 : 4 3. Переведите. 200 мм = … дм 2 530 м = … км … м 600 с = … мин 180 дм = … м … дм 1 500 кг = … т 1 ч 30 мин … мин Домашнее задание: тетрадь № 2, с. 18, № 26, 27; с. 19, № 28–30. У р о к и 95–98 Закрепление пройденного Задания, данные на с. 15–18, учитель использует по своему усмотрению. Часть этих упражнений может быть выполнена устно, часть – с записью и преимущественно самостоятельно. Некоторые упражнения можно использовать на последующих уроках для устного выполнения, самостоятельных и домашних работ. У р о к 99 Деление чисел на произведение Цели: познакомить учащихся с разными способами деления числа на произведение; совершенствовать умения решать задачи. Ход урока I. Организационный момент. II. Устный счёт. 1. Поставьте скобки там, где это необходимо, так, чтобы равенства были верными: 7 · 9 + 12 : 3 – 2 = 23 7 · 9 + 12 : 3 – 2 = 65 7 · 9 + 12 : 3 – 2 = 47 2. Решение задач. Задание 85. Дети читают задачу и составляют к ней по условию буквенные выражения. III. Работа над новым материалом. С разными способами деления числа на произведение можно познакомить, используя записи и иллюстрации в учебнике на с. 19. Учитель. Ребята, откройте учебник на с. 19. Посмотрите рисунок вверху и записи к нему. Объясните, как здесь по-разному нашли результат деления отрезка длиной 12 см на произведение чисел 3 и 2. Дети. Первым способом: вычислили произведение чисел 3 и 2, получилось 6, потом 12 разделили на полученное произведение, получилось 2. Учитель. Верно. На рисунке показали этот способ: отрезок разделили на 6 равных частей. Объясните теперь, как разделили 12 на произведение чисел 3 и 2 вторым способом. Дети. 12 разделили сначала на первый множитель, на 3, и результат 4 разделили на второй множитель, на 2, получилось, как и в первом способе, тоже 2. Учитель. Хорошо. Посмотрите на второй отрезок. Его разделили красными точками на 3 равные части, а потом каждую часть разделили еще на 2 равные части. На сколько равных частей разделили отрезок? Дети. На 6 частей. Учитель. Следовательно, как и в первом случае, здесь тоже разделили число на 6, значит, и так можно делить число на произведение. Теперь объясните третий способ. Дети. 12 сначала разделили на второй множитель, на 2, и полученный результат 6 разделили на первый множитель, на 3, получилось тоже 2. Учитель. Верно. Посмотрите на третий отрезок. Его разделили красной точкой на 2 равные части, а потом каждую часть разделили на 3 равные части. На сколько равных частей разделили отрезок? Дети. Тоже на 6. Учитель. Значит, и так можно делить число на произведение. Повторите, как можно разными способами разделить 12 на произведение чисел 3 и 2. Дети повторяют еще раз эти способы. Для закрепления знания свойства деления числа на произведение надо выполнить задания 82, 83. Выполняя задание 82, ученики еще раз объясняют, как можно по-разному разделить число на произведение. Выполняя задание 83, учащиеся проговаривают вслух, а потом про себя все способы деления числа на произведение, затем в зависимости от чисел выбирают более удобный способ и записывают решение этим способом. Ф и з к у л ь т м и н у т к а IV. Работа над пройденным материалом. Задачу 84 учащиеся решают двумя способами с комментированием у доски.   II с п о с о б: 1) 83 – 45 = 38 (кг) – на столько больше сыра, чем масла из 1 тонны 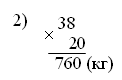 О т в е т: из 20 тонн получается на 760 кг больше сыра, чем масла. V. Итог урока. Учитель. Ребята, что нового узнали на уроке? Дети. Мы познакомились с разными способами деления числа на произведение. Учитель. Что повторяли на уроке? Дети. Повторили решение примеров и задач. Домашнее задание: задание 86; тетрадь № 2, с. 20, № 31; с. 21, № 1. У р о к 100 Прием устного деления, основанный на свойстве деления числа на произведение Цели: познакомить с устным приемом деления, основанным на свойстве деления числа на произведение; повторить деление на 100 и 10; закрепить решение задач на движение и на нахождение площади прямоугольника. Ход урока I. Организационный момент. II. Устный счёт. 1. Найдите значение выражений. (210 – 30) : 9 · (999 + 1) (480 + 320) : 8 · (9 + 91) 70 + 350 : 7 · (10 + 990) 7 200 : (2 + 7) + (140 – 90) 2. Переведите. 9 м2 = … см2 12 ч 50 мин = … мин 14 м2 = … дм2 8 км 9 м = … м 2 000 дм2 = … м2 2 ц 7 кг = … кг III. Работа над новым материалом. В целях подготовки к введению нового приема, основанного на замене делителя произведением, ученики должны выполнить задание 87, называя в каждом случае, на какое число делили и каким произведением заменили делитель. Кроме того, следует предложить детям заменить числа 20, 24, 30 и др. произведением, а потом повторить прием деления на 10 и 100, выполнив задание 95. Объяснение приема можно провести, опираясь на записи в задании 88. |
