поурочные планы математика 4 класс Школа России. поурочные планы математика. Основные требования к знаниям, умениям и навыкам учащихся к концу 4 класса учащиеся должны знать
 Скачать 2.41 Mb. Скачать 2.41 Mb.
|
|
II. Устный счёт. 1. Задание «Головоломка». ? ? О ? О · = 18 · 8 · = 4 · – = 3 2. Задания 161, 162 на с. 34. Дети читают вопросы и отвечают на них. III. Работа над новым материалом. Устный прием умножения на двузначное число могут объяснить сами ученики по записям, данным на с. 34 вверху. Дети. Надо 12 умножить на 15; число 15 заменили суммой разрядных слагаемых 10 и 5; получился пример: 12 умножить на сумму чисел 10 и 5; 12 умножили на 10, на первое слагаемое, затем 12 умножили на 5, на второе слагаемое, и результаты 120 и 60 сложили – получилось 180. Аналогично объясняют решение примера 40 · 32. Задание 156 учащиеся сначала решают с подробным объяснением и развернутой записью по образцу, данному в учебнике, затем решение сопровождают кратким рассуждением и выполняют краткую запись. Например, при вычислении произведения 30 · 16 проговаривают: «30 умножу на 10, получится 300; 30 умножу на 6, получится 180; сложу 300 и 180, получится 480». Запись: 30 · 16 = 480. С целью предупреждения смешения приемов умножения на двузначные числа, оканчивающиеся нулями, выполняются задания 157 и 158. После разбора и решения примеров из задания 157 сделать развернутую запись примеров первой пары из задания 158 на доске и в тетрадях. Затем выяснить отличие приемов вычислений. В первом примере число 12 заменили суммой чисел 10 и 2, а во втором – произведением чисел 2 и 10. В первом примере, умножая число на сумму, умножили его на каждое слагаемое и результаты сложили, а во втором примере, умножая число на произведение, умножили его на первый множитель и результат умножили на второй множитель. Решить примеры второй пары устно, после чего сравнить приемы. Ф и з к у л ь т м и н у т к а IV. Работа над пройденным материалом. 1. Решение задач. Задачу 159 учащиеся решают под руководством учителя двумя способами. После чтения задачи условие записывается в таблицу.
I способ: 1) 20 · 10 = 200 (м) – длина первой канавы 2) 20 · 20 = 400 (м) – длина второй канавы 3) 200 + 400 = 600 (м) II способ: 1) 10 + 20 = 30 (ч) – работал всего 2) 20 · 30 = 600 (м) О т в е т: 600 м всего. Решение задачи 160 ученики тоже выполняют под руководством учителя. После чтения задачи записать краткое условие.  После этого учащиеся составляют план решения и записывают решение в виде отдельных действий. Разбор учитель проводит с теми учащимися, кто не может решить задачу сам. 2. Решение примеров. Задание 163 учащиеся могут выполнить самостоятельно (с последующей проверкой). V. Итоги урока. Учитель. Ребята, что нового узнали на уроке? Дети. Мы изучили устный прием умножения на двузначное число. Учитель. Что повторили на уроке? Дети. Мы повторили решение задач и примеров. Домашнее задание: тетрадь № 2, с. 30, № 1–3. У р о к 117 Письменное умножение на двузначное число Цели: познакомить с приемом письменного умножения на двузначные числа; закрепить умение решать задачи на движение. Ход урока I. Организационный момент. II. Устный счёт. 1. Задание «Занимательные рамки». 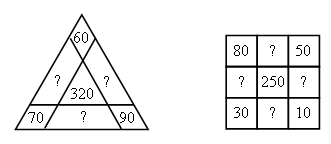 2. Переведите. 18 т 4 ц = … кг 600 см2 = … дм2 3 т 5 кг = … кг 13 дм2 = … см2 18 дм2 = … см2 1 м2 = … дм2 28 ч = … сут. … ч 17 000 см2 = … дм2 III. Работа над новым материалом. При ознакомлении с приемами письменного умножения на двузначное число предложить ученикам выполнить умножение устно, подобрав числа так, чтобы трудно было вычислить неполные произведения, например 69 · 48. Ученики делают на доске запись: 69 · 48 = 69 · (40 + 8) = 69 · 40 + 69 · 8 Учитель объясняет, что вычислить произведение устно в таких случаях трудно, поэтому вычислим письменно. Вызванные ученики записывают решение на доске: 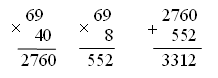 Учитель. Произведения 2 760 и 552 называют неполными; сложив эти произведения, получим произведение чисел 69 и 48, оно равно 3 312. Решение примера 69 · 48 можно записать в столбик короче: подписываем единицы под единицами, а десятки под десятками; умножим 69 на число единиц, на 8, получим первое неполное произведение; умножим 69 на 40: сначала на 4, на число десятков, а потом результат умножим на 10, получим второе неполное произведение; сложим неполные произведения. 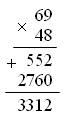 Умножаем 69 на 8: девятью восемь – 72, 2 пишем, 7 запоминаем. И т. д. Умножаем 69 на 40: умножим 69 на 4 и к результату припишем 0; умножаем 69 на 4: четырежды девять – 36, пишем 6 под десятками (оставляем место для 0), а 3 запоминаем. И т. д. Пишем 0 под единицами. Сложим неполные произведения: 2 да 0 – 2, 5 да 6 – 11 и т. д. После этого учащиеся объясняют по учебнику (с. 35 вверху), как умножили 46 на 73. Обращаясь к записи в столбик, данной в учебнике, учитель объясняет: «Нуль в конце второго неполного произведения можно не писать, так как, сложив число единиц первого неполного произведения с этим нулем, всегда получим число единиц первого неполного произведения. В дальнейшем не будем писать этот нуль, но при умножении на число десятков начнем подписывать второе неполное произведение под десятками первого неполного произведения». После этого учащиеся объясняют по записям, данным в задании 165, как умножили 68 на 45, 86 на 53 и 96 на 16. Затем выполняют задание 166: вслух подробно объясняют решение каждого примера, записывая в столбик. Ф и з к у л ь т м и н у т к а IV. Работа над пройденным материалом. Задачу 167 учащиеся решают самостоятельно. Одного учащегося можно вызвать решать на закрытую доску, а потом произвести проверку. Условие задачи записывается чертежом. V. Итоги урока. Учитель. Ребята, что нового узнали на уроке? Дети. Сегодня на уроке мы учились умножать на двузначное число столбиком. Учитель. Что повторили на уроке? Дети. Мы повторили решение задач на движение. Домашнее задание: задание 168; тетрадь № 2, с. 31, № 4–7. У р о к 118 Умножение на двузначные числа Цели: продолжить работу по ознакомлению с умножением на двузначные числа; рассмотреть умножение трехзначных и четырехзначных чисел; закрепить умение решать задачи и уравнения. Ход урока I. Организационный момент. II. Устный счёт. 1. Найдите лишнее выражение. 240 : 2 360 : 3 600 : 5 120 · 1 480 : 4 720 : 6 1 200 : 10 2. Задание 24 на с. 45. Дети рассматривают таблицу, данную в учебнике, и составляют по ней буквенные выражения. III. Работа над новым материалом. По записи в задании 169 дети под руководством учителя объясняют, как выполнено умножение трехзначных и четырехзначных чисел на двузначные числа. Затем решают с комментированием у доски задание 170. Ф и з к у л ь т м и н у т к а IV. Работа над пройденным материалом. 1. Решение задач. Задачу 171 учащиеся решают под руководством учителя. После чтения задачи дети записывают условие в таблицу, а затем записывают решение по действиям столбиком.   О т в е т: 24 м ткани сэкономили всего. Задачу 172 учащиеся читают, после этого записывают условие под руководством учителя. 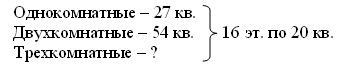 Решение задачи ученики выполняют самостоятельно, разбор учитель проводит с теми учащимися, кто не сможет сам решить задачу. 2. Решение примеров. Задание 175 учащиеся выполняют самостоятельно (с последующей проверкой). Дети должны сначала записать примеры, а потом их решить. V. Итоги урока. Учитель. Ребята, над чем работали на уроке? Дети. Мы продолжали учиться умножать на двузначные числа. Мы также закрепляли решение задач и примеров. Домашнее задание: задание 176; тетрадь № 2, с. 32, № 8–10. У р о к 119 Решение задач на нахождение неизвестных по двум разностям Цели: познакомить с решением задач на нахождение неизвестных по двум разностям; закрепить знания, умения и навыки по пройденному материалу. Ход урока I. Организационный момент. II. Устный счёт. 1. Задание «Занимательная рамка».
2. Сравнение долей. Задание 181, с. 37. Дети рассматривают рисунок и сравнивают доли по заданию. III. Работа над новым материалом. Перед введением задач нового вида полезно предложить ученикам задачи такого вида: 1) Дима и Алеша купили почтовые марки по одинаковой цене: Дима – 2 марки, а Алеша – 5 марок. Кто из мальчиков купил больше марок? На сколько больше? Кто из них уплатил денег больше? 2) Алеша купил на 3 марки больше, чем Дима, и уплатил на 12 руб. больше, чем Дима. Сколько стоила одна почтовая марка? Ученики выполняют к первой задаче рисунок: каждую марку изображают клеточкой, располагая их в два ряда. Учитель обращается к классу: «Ответьте на вопрос первой задачи. За сколько марок Алеша уплатил столько же денег, сколько уплатил Дима?». Учитель читает вторую задачу. Беседа продолжается: «Что значит «Алеша купил на 3 марки больше, чем Дима?». Покажите это на рисунке. Что значит «Уплатил на 12 р. больше?». За сколько марок Алеша уплатил 12 р.? Сколько стоит одна марка? Как узнали?». После этого учитель предлагает открыть учебник на с. 37 и прочитать задачу 177 (1). Учитель делает на доске иллюстрацию, изобразив куски ткани отрезками. 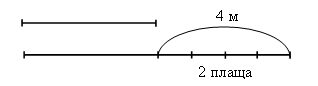 Учитель. На сколько метров ткани было больше во втором куске, чем в первом? Дети. На 4 м. Учитель. Что это значит? Дети. Было столько же и еще 4 м. Учитель. Изобразим это отрезками: столько же, сколько в первом куске и еще 4 м. На сколько больше сшили плащей из второго куска, чем из первого? Дети. На 2 плаща. Учитель. Покажите на отрезке, из какой ткани сшили 2 плаща. Дети. Из 4 м. Учитель. Как узнаете, сколько метров ткани расходовали на 1 плащ? Дети. 4 : 2 = 2. Учитель. А на 6 плащей? Дети. 2 · 6 = 12 (м). Теперь можно перейти к решению задачи 177 (2). Сначала коллективно выполняется чертеж на доске и в тетрадях: куски ткани изображаются отрезками 6 см и 10 см.  Учитель. Почему из второго куска сшили больше плащей? Дети. В нем больше материи. Учитель. Сколько метров ткани второго куска пошло на пошив такого же количества плащей из первого куска? Дети. 6 м. Учитель. Сколько плащей сшили из остальной ткани второго куска? Дети. 2 плаща. Учитель. Можно ли узнать, сколько метров ткани шло на один плащ? Дети. Можно. Учитель. Составьте план решения. Решение можно записать в виде отдельных действий с пояснением. 1) 10 – 6 = 4 (м) – пошло на 2 плаща 2) 4 : 2 = 2 (м) – на 1 плащ 3) 2 · 8 = 16 (м) О т в е т: 2 м пошло на 1 плащ, 16 м пошло на 8 плащей. После чтения задачи 178 разбирают ее, применяя при разборе и объяснении ту методику, которая была использована при решении предыдущей задачи. Эту задачу целесообразно после чтения записать кратко на доске и в тетрадях, выделив сначала величины.  Можно сделать чертеж. 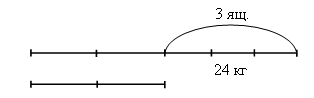 1) 5 – 2 = 3 (ящ.) – вмещают 24 кг 2) 24 : 3 = 8 (кг) – в 1 ящике 3) 8 · 5 = 40 (кг) 4) 8 · 2 = 16 (кг) О т в е т: 40 кг привезли в 1-ю столовую, 16 кг – во 2-ю столовую. Ф и з к у л ь т м и н у т к а IV. Работа над пройденным материалом. Задание 179 можно предложить учащимся решить самостоятельно (с последующей проверкой). V. Итоги урока. Учитель. Ребята, что нового узнали на уроке? Дети. Мы познакомились с новым видом задач. Учитель. Что закрепляли на уроке? Дети. Мы закрепляли прием умножения на двузначные числа. Домашнее задание: задания 180, 182; тетрадь № 2, с. 33, № 11, 12. У р о к 120 Решение задач Цели: закрепить умение решать задачи на нахождение неизвестных по двум разностям; закрепить умение выполнять деление на числа, оканчивающиеся нулями; повторить отношение единиц площади. Ход урока I. Организационный момент. II. Устный счёт. 1. Заполните таблицу из задания 188 на с. 38 (вынести на доску). Перед заполнением таблицы учащиеся должны вспомнить правила: как найти неизвестное делимое и неизвестный делитель.
2. Задание «Арифметические ребусы». 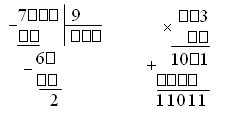 3. Задание 186 на с. 38 (можно тоже вынести на доску). 1 см2 – 10 мм2 1 м2 – 10 дм2 1 дм2 – 5 см2 1 см2 – 1 мм2 1 м2 – 1 000 см2 1 дм2 – 50 см2 III. Работа над пройденным материалом. 1. Задачу 183 (1) учащиеся решают под руководством учителя. Прочитав задачу, дети кратко записывают ее в таблицу, выделив величины.  После этого предложить учащимся самостоятельно составить план решения и записать решение в виде отдельных действий. Разбор провести с теми учениками, кто не сможет решить задачу сам. Используя ответ предыдущей задачи и чертеж, дети узнают, сколько метров линолеума шириной 2 м потребуется, чтобы покрыть полы в зале и коридоре. Задачу 184 учитель тоже разбирает вместе с учащимися. После чтения задачи дети выделяют данные в ней величины и записывают условие в таблицу. Затем решают с комментированием у доски, отдельно записывая каждое действие.  1) 6 – 4 = 2 (ч) – потребовалось на 1 400 км 2) 1 400 : 2 = 700 (км/ч) – скорость 3) 700 · 4 = 2 800 (км) 4) 700 · 6 = 4 200 (км) О т в е т: 1-й самолет пролетел 2 800 км, 2-й самолет – 4 200 км. |
