Реализация LU разложения с помощью функций IMSL. ОТЧЕТ БИРЮКОВКО КОМПАКТНЫЙ. Отчет на тему
 Скачать 182.56 Kb. Скачать 182.56 Kb.
|
Листинг программы двойной точностиprogram double implicit none INTEGER*4 IPATH, LDA, LDFAC, N, NLCA, NUCA, IPATH2, LDFAC2, NLCA2, NUCA2, NOUT, IPATH3,, NLCA3, NUCA3, j, k, i PARAMETER (IPATH=1, LDA=7, LDFAC=10, N=8, NLCA=3, NUCA=3, IPATH2=1, LDFAC2=10, NLCA2=3, NUCA2=3, IPATH3=1, NLCA3=3, NUCA3=3) INTEGER IPVT(N), IPVT2(N) REAL*8 A(LDA,N),z(N,4) , p(10500000,8) REAL*8 FAC2(LDFAC,N2), RCOND, FAC(LDFAC,N) REAL*8 X(N,2), RES(N), AINV(N,N), B(N,4), RJ(N) REAL T,Timef EXTERNAL DLFTRB, DLFSRB, DWRRRN, DLFCRB, DLFIRB, DSET, UMACH, DLSLRB T=Timef() do i=1,10500000 do j=1,8 p(i,j) = i+j END DO END DO do i = 1,10500000,7 do j = 1,8,1 A(1,j)=p(i,j) A(2,j)=p(i+1,j) A(3,j)=p(i+2,j) A(4,j)=p(i+3,j) A(5,j)=p(i+4,j) A(6,j)=p(i+5,j) A(7,j)=p(i+6,j) END DO !Зададим правую часть линейной системы DO k=1,N DO j=1,4 z=j+k B(k,j)=z END DO END DO !решение исходного уравнения CALL DLFTRB (N, A, LDA, NLCA, NUCA, FAC, LDFAC, IPVT) !решение для правых сторон DO 10 J=1, 4 CALL DLFSRB (N, FAC, LDFAC, NLCA, NUCA, IPVT, B(1,J), IPATH, X(1,J)) 10 CONTINUE !вывод результатов ! CALL DWRRRN ('X', N, 2, X, N, 0) !решение исходного уравнения CALL DLFCRB (N, A, LDA, NLCA2, NUCA2, FAC2, LDFAC2, IPVT2, RCOND) ! Вывод оценки числа обусловленности ! CALL UMACH (2, NOUT) ! WRITE (NOUT,99999) RCOND, 1.0E0/RCOND CALL DSET (N, 0.0E0, RJ, 1) DO 20 J=1, N RJ(J) = 1.0E0 CALL DLFIRB (N, A, LDA, NLCA2, NUCA2, FAC2, LDFAC2, IPVT2, RJ, IPATH2, AINV(1,J), RES) RJ(J) = 0.0E0 20 CONTINUE !вывод результатов ! CALL DWRRRN ('AINV', N, N, AINV, N, 0) ! 99999 FORMAT (' RCOND = ',F5.3,/,' L1 Condition number = ',F6.3) !решение исходного уравнения CALL DLSLRB (N, A, LDA, NLCA3, NUCA3, B, IPATH3, X3) !вывод результатов ! CALL DWRRRN ('X', 1, N, X3, 1, 0) END DO T=Timef() PRINT *,' TIME: ',T end program double Результаты измерений времени выполнения расчета.Параметры системы: Операционная система: Windows 10 Pro Тип системы: 64-разрядная ОС, процессор х64 Модель ПК: ASUS ZenBook 14 UX433 Процессор: AMD Ryzen 5 3500U with Radeon Vega Mobile Gfx 2.10 GHz Установленная память (ОЗУ): 8,00 Гб (зарезервировано аппаратно 2 Гб) Количество ядер: 4 Количество логических процессоров: 8 Таблица 4. Время выполнения расчетов.
Таблица 5. Время выполнения параллельных расчетов.
Обработка результатов. В процессе работы была написана расчетная программа на языке высокого уровня Fortran. Она удовлетворяет задаче существенного заполнения RAM компьютера. Занимаемая оперативная память компьютера находится в диапазоне 300‐400 Мб. Для правильной оптимизации расчетного оборудования и отражения специфики работы программ ЯЭ учебная программа считает не менее 40 сек. Для определения времени работы, в программу был встроен счетчик, который включается перед началом основного расчета, и выключается после того, как будет найдено решение заданной системы процедур и расчет будет окончен. В конце программы организуется вывод на экран времени счета. Для компактного оформления расчета значения измерений в формулы подставляться не будут. Все данные ранжированы с помощью специальной функции Excel. Расчет на одном и том же компьютере одной версии программы с одинарной точностью в debug режиме. Математическое ожидание ( М ) найдем как среднее арифметическое значений элементов выборки. Найдем по формуле:  , где , где  = =  – значения элементов, – значения элементов,N = 90 – количество элементов. М = 70.630 с. Медиана (Ме) – среднее арифметическое значений двух элементов ранжированной выборки, приходящихся на её середину. В нашем случае это значения под номерами 44 и 45.  , ,Ме = 70.647 с. Дисперсия выборки ( D ) – степень квадратичного отклонения каждого измеренного значения от мат. ожидания. Найдем по формуле:  . .D = 0.02037 Среднеквадратичное отклонение (σ) – абсолютное отклонение измеренных значений элементов выборки от среднеарифметического значения. Найдем по формуле:  . .σ = 0.1427 Размах выборки (R) – Разница между максимальным и минимальным значениями выборки. Найдем по формуле:  . .R = 0.667 Середину размаха выборки (Rср) найдем по формуле:  . .Rср = 70.547 с. Мода (М0) – наиболее часто встречающееся значение элемента выборки. М0 = 70.214 с. Оценка количества интервалов выборки (m): 1 + 3,322 ∙ lg(𝑁) < 𝑚 < 5 ∙ lg(𝑁) 7,49 < 𝑚 < 9,77 Выберем количество интервалов: m = 8 Ширину интервала (S) для дальнейшего построения гистограмм определим по формуле:  . .Определим количество значений элементов в интервале – частоту (n): Начиная с наименьшего значения (70.214) двигаемся с шагом S.
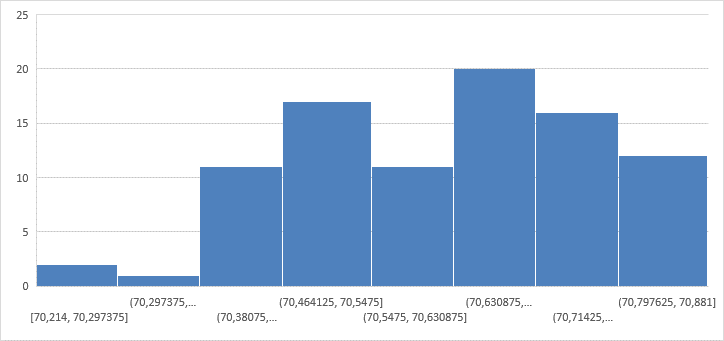 Рис. 1. Гистограмма для 𝑻 𝟗𝟎д Асимметрия (А) – симметричность расположения значений элементов выборки относительно математического ожидания. Найдем по формуле:  . .A = -0.31, основная часть значений элементов выборки меньше математического ожидания. Эксцесс (Е) – показатель остроты пика распределения значений выборки. Найдем по формуле: 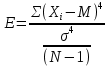 . .E = -0.278, Значения элементов выборки распределены по всей области значений. Расчет объема элементов выборки в интервалах М ± σ и М ± 2σ М + 𝜎 = 70.630 + 0,14932 = 70.77932 с. М – 𝜎 = 70.630 − 0,14932 = 70.48068 с. М + 2 ∙ 𝜎 = 70.630 + 2 ∙ 0,14932 = 70.92864 с. М − 2 ∙ 𝜎 = 70.630 − 2 ∙ 0,14932 = 70.33136 с. Известно, что нормальное распределение подчиняется правилу «трех сигм»: в пределах одного СКО лежит 68,26% значений элементов выборки, а в пределах двух – 95,44%. Рассчитаем объём элементов выборки в интервалах M±σ и M±2σ
Распределение можно считать нормальным. Проведем вычисления для остальных случаев по такому же алгоритму: Расчет на одном и том же компьютере одной версии программы с одинарной точностью в оптимизированном режиме. Математическое ожидание ( М )  , где , где  = = 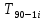 – значения элементов, – значения элементов,N = 90 – количество элементов. М = 65.6343 с. Медиана (Ме)  , Ме = 65.647 с. , Ме = 65.647 с.Дисперсия выборки ( D )  . D = 0.016962. . D = 0.016962.Среднеквадратичное отклонение (σ)  . σ = 0.130237. . σ = 0.130237.Размах выборки (R)  . R = 0.512. . R = 0.512.Середина размаха выборки (Rср)  . Rср = 65.635c. . Rср = 65.635c.Мода (М0) М0 = 65.655 с. Оценка количества интервалов выборки (m): 1 + 3,322 ∙ lg(𝑁) < 𝑚 < 5 ∙ lg(𝑁) 7,49 < 𝑚 < 9,77 Выберем количество интервалов: m = 8 Ширину интервала (S) для дальнейшего построения гистограмм определим по формуле:  . .Определим количество значений элементов в интервале – частоту (n):
 Рис. 2. Гистограмма для 𝑻 𝟗𝟎−1. Асимметрия (А)  . . A = 0.033 0, симметрия, характерная для нормального распределения. Эксцесс (Е) 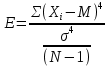 . .E = -0.9568, значения элементов выборки распределены по всей области значений. Расчет объема элементов выборки в интервалах М ± σ и М ± 2σ М + 𝜎 = 65.6343 + 0.13024 = 65.7645 с. М – 𝜎 = 65.6343 – 0.13024 = 65.5041 с. М + 2 ∙ 𝜎 = 65.6343 + 2 ∙ 0.13024 = 65.8948 с. М − 2 ∙ 𝜎 = 65.6343 − 2 ∙ 0.13024 = 65.3738 с.
Распределение можно считать нормальным. Расчет на одном и том же компьютере одной версии программы с двойной точностью в оптимизированном режиме. Математическое ожидание ( М )  , где , где  = = 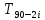 – значения элементов, – значения элементов,N = 90 – количество элементов. М = 114.3472 с. Медиана (Ме)  , Ме = 114.329 с. , Ме = 114.329 с.Дисперсия выборки ( D )  . D = 0.017303. . D = 0.017303.Среднеквадратичное отклонение (σ)  . σ = 0.131541. . σ = 0.131541.Размах выборки (R)  . R = 0.492. . R = 0.492.Середина размаха выборки (Rср)  . Rср = 114.354 c. . Rср = 114.354 c.Мода (М0) М0 = 114.27 с. Оценка количества интервалов выборки (m): 1 + 3,322 ∙ lg(𝑁) < 𝑚 < 5 ∙ lg(𝑁) 7,49 < 𝑚 < 9,77 Выберем количество интервалов: m = 8 Ширину интервала (S) для дальнейшего построения гистограмм определим по формуле:  . .Определим количество значений элементов в интервале – частоту (n):
 Рисунок 3. Гистограмма для 𝑻 𝟗𝟎−2. Асимметрия (А)  . . A = 0.127 , основная часть значений элементов выборки больше математического ожидания. Эксцесс (Е) 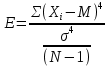 . .E = -0.9693, значения элементов выборки распределены по всей области значений. Расчет объема элементов выборки в интервалах М ± σ и М ± 2σ М + 𝜎 = 114.3472 + 0.13154 = 114.47874 с. М – 𝜎 = 114.3472 – 0.13154 = 114.21566 с. М + 2 ∙ 𝜎 = 114.3472 + 2 ∙ 0.13154 = 114.61028 с. М − 2 ∙ 𝜎 = 114.3472 − 2 ∙ 0.13154 = 114.08412 с.
Распределение можно считать нормальным. Построение коэффициентов корреляции. Коэффициент корреляции (r)- показатель, величина которого варьируется в пределах от -1 до 1. Показывает степень взаимосвязи между двумя показателями.
Коэффициент корреляции между множеством измерений программ одинарной и двойной точности в оптимизированном режиме: Значение корреляции вычислим с помощью внутренней функции Excel. r1 = 0.031564.  Рис 4. Зависимость измерений Т 90−1 и Т 90−2 от времени. Коэффициент корреляции между множеством измерений программ одинарной точности в оптимизированном режиме и в debug режиме: Значение корреляции вычислим с помощью внутренней функции Excel. r2 = 0.021342. 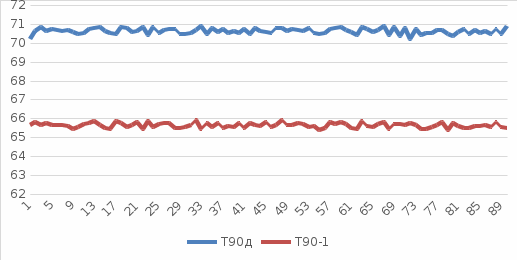 Рис 5. Зависимость измерений Т 90−1 и Т 90д от времени. Коэффициент корреляции между множеством измерений программ двойной точности в оптимизированном режиме и в debug режиме: Значение корреляции вычислим с помощью внутренней функции Excel. r2 = 0.067870. 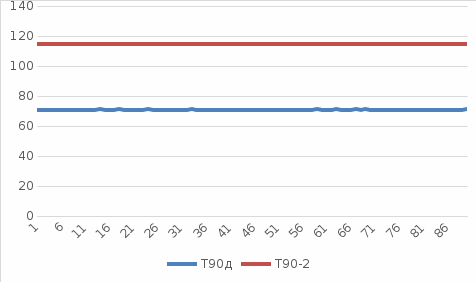 Рис 6. Зависимость измерений Т 90−2 и Т 90д от времени. Производительность при выполнении параллельных расчетов. По приведенным выше данным можно построить график зависимости времени выполнения программы от количества выполняемых программ, по сути, данный график и будет показателем производительности: 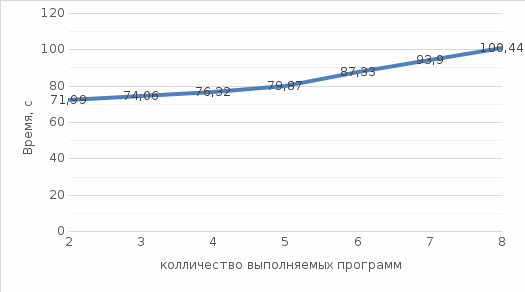 Рис 7. Производительность при выполнении параллельных расчетов программ. А также приведем зависимости времени выполнения каждого расчета при проведении параллельных вычислений: 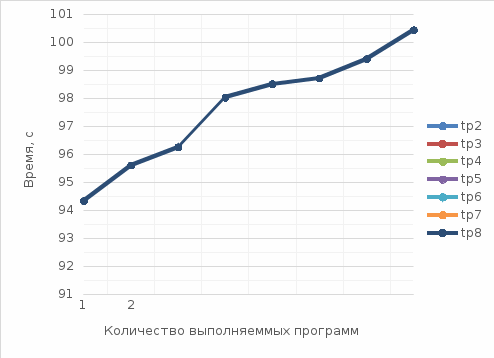 Рис 8. Производительность при выполнении параллельных расчетов с учетом выполнения каждой программы. Вывод. При выполнении данной работы была написана программа в среде программирования Visual Fortran с использованием математической библиотеки IMSL. Были проведены тестовые расчеты программы с целью проверки производительности компьютера и составлен отчет. Программы одинарной и двойной точности были запущены в нескольких режимах, а именно: в debug режиме и в оптимизированном режиме. Как видно, при выполнении программы в debug режиме, время ее работы незначительно больше времени выполнения той же программы, но скомпилированной в режиме. Это объясняется тем, что практически все вычислительные процессы происходили в процедуре IMSL, которая уже скомпилирована. Переключение режимов компиляции сказывается только на времени выполнения той подготовительной части программы, которая была написана непосредственно нами. Поскольку суммарный вклад во время выполнения этой части мал, разница во времени выполнения также мала. Распределение времени расчета на одном и том же компьютере одной версии программы происходит по нормальному закону. Об этом говорит сравнение значений мат. ожидания, медианы и середины размаха выборки (они отличаются друг от друга менее чем на процент), а также сравнение полученных данных о распределении элементов выборки с теоретическими данными по закону «трех сигм». Из полученных графиков (рис. 4-6) видно, что корреляции между множеством измерений программ не наблюдается, как и ожидалось. Следовательно, взаимосвязи между данными значениями нет. Объем занимаемой памяти прямо пропорционально связан со временем выполнения расчета, то есть чем больше памяти будет занимать буферный массив, тем дольше он будет обрабатываться. Из полученных графиков (Рис. 7, 8) видно, что с ростом числа запущенных процессов, мы получаем общее замедление выполнения программ. Это объясняется тем, что в ОС реализована система разделения времени: каждой задаче выделяется квант процессорного времени, в течение которого она может занимать процессор. По истечении этого времени задача вытесняется, и запускается следующая. Различие между временем выполнения для одинарной и двойной точности связано с тем, что при расчете с двойной точностью одно значение реального типа данных занимают 8 байт места в памяти, а при одинарной точности 4 байта, что в свою очередь, приводит к обработке больших объемов данных, следовательно, к повышению времени выполнения самой программы. Список литературы1. Ю. Б. Воробьев Методические указания по проведению лабораторных работ по дисциплине "Компьютерные и сетевые технологии ЯЭ". 2. IMSL. Math Library. Volumes 1 and 2. 3. О. В. Бартеньев «Фортран для профессионалов. Математическая библиотека IMSL» 4. Л. С. Шихобалов «Матрицы и определители». | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
