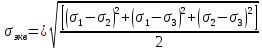курсовая работа сопромат. Отчет по курсовой работе на тему Расчет и проектирование вала, работающего в условиях многоциклового характера нагружения
 Скачать 0.53 Mb. Скачать 0.53 Mb.
|
|
Министерство науки и высшего образования Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования «ПЕРМСКИЙ НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ» Аэрокосмический факультет кафедра «Механика композиционных материалов и конструкций» направление: 24.05.02 «Проектирование авиационных и ракетных двигателей» ОТЧЕТ по курсовой работе на тему: «Расчет и проектирование вала, работающего в условиях многоциклового характера нагружения» Вариант 20 Выполнил студент группы АД-18-1с: Хабиров Арыслан Ряисович _________________________________ (подпись) Проверил: доц. кафедры МКМК Макарова Е.Ю. _______ ____________________ (оценка) (подпись) МП _____________ (дата) Пермь 2020 Содержание Введение…………………………………………………………………………... 3 §1. Сложное сопротивление…………………………………………….………4 1.1. Косой изгиб…………………………………………………………………4 1.2. Изгиб с кручением…………………………………………………………. 5 1.3. Внецентренное растяжение-сжатие…………………………………...…..7 1.4. Изгиб с растяжением………………………………………………………. 8 §2. Гипотезы прочности………………………………………………………..10 2.1. Коэффициентом запаса прочности…………………………………..…..10 2.2. Равноопасное состояние……………………………………….…………10 2.3. Эквивалентное напряжение.…………………………..………………….10 2.4. Причины появления и разновидности гипотез прочности……………..11 §3. Усталость и выносливость материалов при циклических нагрузках………………………………………………………………...………14 3.1. Понятия усталости и выносливости …………………………………….14 3.2. Основные характеристики цикла и знакопеременных нагрузок …………………………………………………..15 3.3Предел выносливости………………………………………………………16 3.4 Диаграмма усталостной прочности……………………………………….17 4. Расчет на прочность вала при изгибе с кручением…………………… 19 5. Расчет вала на сопротивление многоцикловой усталости…………… 22 6. Выводы………………………………………………………………………... 29 7. Список литературы…………………………………………………………… 30 Введение В сфере технологий и промышленности всегда были актуальны вопросы долговечности и прочности механизмов и деталей машин. Многие составные части конструкций и устройств работают и выполняют свои функции под действием циклических нагрузок и напряжений. Это силовые воздействия, которые периодически изменяются во времени. Такие нагружения опасны по своей природе, так как при длительном воздействии влекут за собой необратимые процессы накопления повреждений, которые приводят к образованию трещин в полости и снаружи деталей. Этот процесс называется «усталостью» материалов, из которых состоят детали. Именно поэтому очень важно уметь рассчитывать напряжения при работе различных конструкций, подбирать конструкционные материалы, способные выдерживать данные нагрузки, в целом проектировать механизмы и подбирать их оптимальные параметры. Цели данной курсовой работы: 1. Проектирование вала с расчетом его прочности при изгибе с кручением 2. Расчет сопротивления вала многоцикловой усталости. Задачи: Изучить теоретический материал, необходимый для проведения расчетов. Определить горизонтальные и вертикальные составляющие реакций. Построить эпюры крутящих и изгибающих моментов. Определить диаметр вала из условия прочности по гипотезе наибольших касательных напряжений. Определить диаметры вала из условия статической прочности в указанных сечениях и спроектировать ступенчатый вал, округлив диаметры ступеней до стандартного размера. Определить фактический запас прочности вала при циклических нагрузках. Рассчитать запас прочности по нормальным напряжениям с учетом усталости в опасных сечениях, считая концентраторами напряжений уступ с галтелью и шпоночный паз, необходимый для закрепления на валу шкивов с помощью шпонок. Проделать такой же расчет для определения запасов прочности по касательным напряжениям. Цикл касательных напряжений считать пульсирующим. Рассчитать полный запас прочности с учетом усталости материала. §1. Сложное сопротивление Сложное сопротивление – это вид нагружения, при котором в поперечном сечении действуют одновременно несколько видов усилий. Порядок решения задач при сложном сопротивлении: Определение внутренних усилий методом сечений + черчение эпюр. Определение касательного и нормального напряжений от действия каждого внутреннего усилия. Определение опасных сечений и опасных точек. Находим и записываем условия прочности в данных точках. Можно утверждать, что напряжение от нескольких силовых факторов равно сумме напряжений от каждого из них в отдельности (принцип независимости действия сил). Распространенные комбинации нагружений: 1) Косой изгиб 2) Изгиб с кручением 3) Внецентренное растяжение-сжатие 4) Изгиб с растяжением 1.1. Косой изгиб Косой изгиб – это изгиб, при котором плоскость действия изгибающего момента не совпадает ни с одной из главных плоскостей инерции сечения бруса. В общем случае, при косом изгибе в поперечных сечениях возникают четыре внутренних силовых фактора: поперечные силы Qx, Qy и изгибающие моменты Mx , My. Таким образом, косой изгиб можно рассматривать как сочетание двух плоских поперечных изгибов во взаимно перпендикулярных плоскостях. Влиянием поперечных сил на прочность и жесткость бруса обычно пренебрегают. 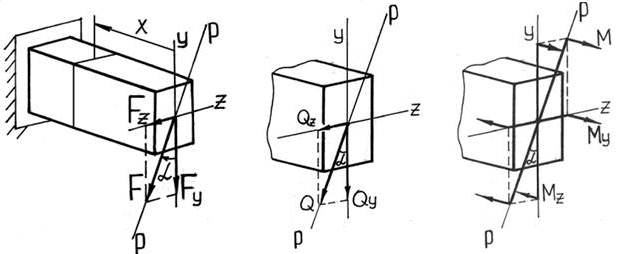 Рис.1. Модель усилий при косом изгибе Условие прочности при косом изгибе: 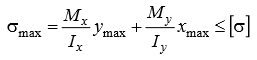 где ymax, xmax — координаты точки сечения, наиболее удаленной от нейтральной оси. Для сечений, имеющих две оси симметрии, максимальные напряжения будут в угловых точках, а условие прочности: 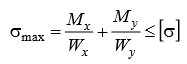 где Wx, Wy – осевые моменты сопротивления сечения относительно соответствующих осей. 1.2. Изгиб с кручением Сочетание деформаций изгиба и кручения характерно для работы валов машин. 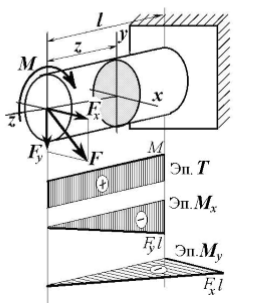 Рис. 2 Эпюры при изгибе с кручением цилиндрического стержня Напряжения в сечениях вала возникают от кручения и от изгиба. При изгибе появляются нормальные и касательные напряжения: 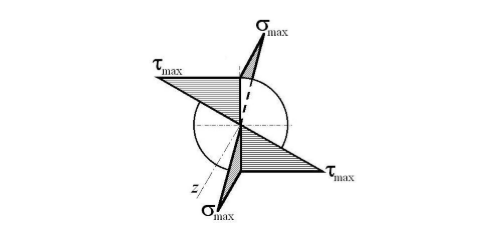 Рис.3 Эпюры напряжений в сечении бруса при кручении с изгибом Нормальное напряжение достигает максимума на поверхности: 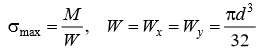 Касательное напряжение от крутящего момента Mz достигает максимума также на поверхности вала: 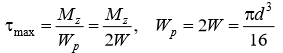 Из третьей и четвёртой теории прочности: 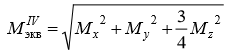 При кручении с изгибом условие прочности имеет вид: 1.3. Внецентренное растяжение-сжатие При таком виде сложного сопротивления продольная сила приложена не в центре тяжести поперечного сечения бруса. Внецентренным растяжением-сжатием называется случай, когда равнодействующая сил, приложенных к отброшенной части стержня, направлена параллельно оси стержня, но не совпадает с этой осью 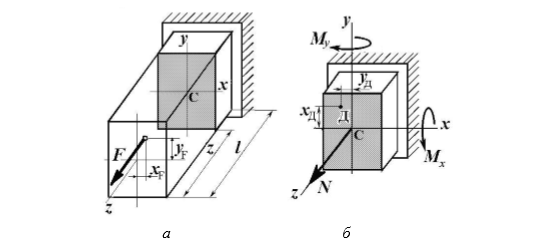 Рис. 4 К расчёту на прочность бруса при внецентренном растяжении a - нагружение бруса; б - внутренние силовые факторы в поперечном сечении; Приведём силу F к центру тяжести: 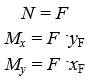 где уF , xF — координаты точки приложения силы F. В произвольной точке Д, с координатами (хд, уд), нормальное напряжение определяется по фомуле: 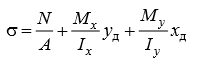 Условие прочности для бруса, изготовленного из материала, одинаково сопротивляющегося растяжению и сжатию, имеет вид: 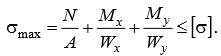 1.4. Изгиб с растяжением При таком виде сложного сопротивления внутренние силовые факторы приводятся к одновременному действию продольной силы N и изгибающего момента M. Рассмотрим случай центрального растяжения бруса в сочетании с косым изгибом. На консольный брус действует сила F, составляющая некоторый угол с продольной осью бруса и не лежащая ни в одной из главных плоскостей сечения. Сила приложена в центре тяжести торцевого сечения бруса: 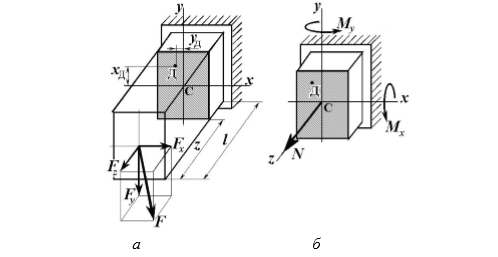 Рис. 5 К расчёту на прочность бруса при изгибе с растяжением: a - нагружение бруса; б - внутренние силовые факторы в поперечном сечении; Разложим силу F на три составляющие. Тогда внутренние силовые факторы приобретут следующий вид: 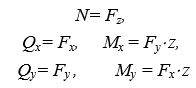 Напряжение в произвольно выбранной точке Д, имеющей координаты (хд, уд), пренебрегая действием поперечных сил, будут определяться по формуле: 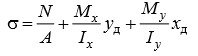 , где А — площадь поперечного сечения. , где А — площадь поперечного сечения.Если сечение имеет две оси симметрии (двутавр, прямоугольник, круг), наибольшее напряжение определяют по формуле: 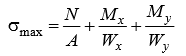 [1]. [1].§2. Гипотезы прочности 2.1. Коэффициентом запаса прочности при сложном напряженном состоянииназывается число, на которое следует умножить все компоненты тензора напряжений (или s1, s2, s3), чтобы данное напряженное состояние стало предельным. (Рис. 6) 2.2. Равноопасными называются такие напряженные состояния, для которых коэффициенты запаса прочности равны. Это дает возможность сравнивать все напряженные состояния между собой, заменяя их равноопасным одноосным напряженным состоянием (растяжением). 2.3. Эквивалентным напряжением называется напряжение, которое следует создать в растянутом образце, чтобы его напряженное состояние стало равноопаснымзаданному напряженному состоянию (Рис. 6) 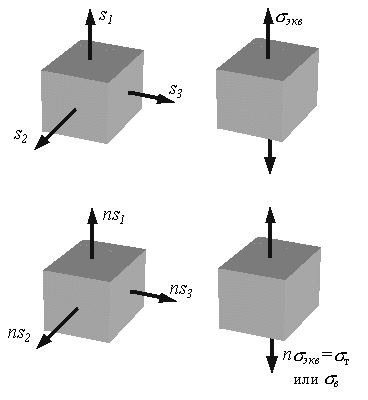 Рис. 6 2.4. Причины появления и разновидности гипотез прочности Установлено, что в каждой точке нагруженного тела, в общем случае действует три главных напряжения. Поэтому, чтобы судить о прочности материала при сложном напряженном состоянии, нужно предварительно знать в какой момент при той или иной комбинации главных напряжений наступает опасное состояние материала. При сложном напряженном состоянии решение этой задачи значительно сложнее, т. к. число различных сочетаний из главных напряжений неограниченно велико, а опыт технически очень сложен. В следствие этого при составлении условий прочности материала при сложном напряженном состоянии мы можем располагать только допускаемыми напряжениями, установленными по результатам испытаний на простое растяжение или сжатие. В связи с этим возникает задача: зная максимально допустимые безопасные напряжения при простом растяжении, найти эквивалентную, т. е. равно безопасную комбинацию из главных напряжений при сложном напряженном состоянии. Единственным практическим путем решения этой задачи является установление общих критериев разрушения, которые позволили бы оценить опасность перехода материала в предельное состояние при сложном напряженном состоянии, используя лишь данные опытов на растяжение. Рассмотрим гипотезы прочности – критерии эквивалентности напряженных состояний. Применение гипотез прочности избавляет от необходимости проведения огромного количества экспериментов. Тот или иной критерий эквивалентности может быть основой для практических расчетов на прочность лишь при условии, что для ряда частных случаев он проверен опытным путем, и результаты эксперимента оказались достаточно близки к результатам теоретического расчета. Определение истинной причины разрушения материала является труднейшей задачей. Это обстоятельство не позволяет создать единую общую гипотезу прочности и повлекло за собой появление многих теорий, каждая из которых основывается на своей гипотезе о причине разрушения материала (табл. 1). Выбор гипотезы прочности зависит от того, в хрупком или пластическом состоянии находится материал. Для каждой гипотезы условие прочности будет записано так: σэкв ≤ [σ] [2]. Таблица 1. Гипотезы прочности [3]
Первая гипотеза прочности была предложена Галилеем. Согласно ей, причина разрушения материала – наибольшее по абсолютному значению нормальное напряжение. Очевидный недостаток первой гипотезы в том, что она не учитывает два других главных напряжения (которые так же вносят свой определенный вклад в напряженное состояние), поэтому на сегодняшний день она не применяется. Однако эта гипотеза может быть использована в случае одноосного растяжения хрупкого материала при условии малости двух главных напряжений по сравнению с третьим. Вторая гипотеза прочности была разработана Мариоттом и Сен-Венаном. Она основывается на предположении, что причина разрушения – наибольшие линейные деформации. Вторая гипотеза более приближена к реальности, чем первая, так как она учитывает все три главных напряжения. Тем не менее, гипотеза допускает сохранение закона Гука вплоть до предела текучести (предела прочности для хрупких материалов), что является крайне грубым приближением. Как и предыдущая гипотеза, в наше время не используется. Третья гипотеза прочности говорит о том, что основной вклад в разрушение материала вносят наибольшие касательные напряжения. Хотя гипотеза и не учитывает главного напряжения 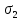 , она, тем не менее, хорошо подтверждается в экспериментах. Ошибка от пренебрежения , она, тем не менее, хорошо подтверждается в экспериментах. Ошибка от пренебрежения 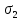 составляет не более 15%. Была предложена Кулоном. составляет не более 15%. Была предложена Кулоном.Четвертая гипотеза прочности основывается на том, что количество удельной потенциальной энергии изменения формы в момент предельного напряженного состояния одинаково как для одноосного растяжения, так и для сложного напряженного состояния. Преимущество гипотезы в том, что она учитывает все главные напряжения. Она может использоваться для пластичных материалов. Была разработана Губером. Гипотеза прочности Мора рекомендуется для хрупких материалов, так как она учитывает неодинаковость сопротивления материалов сжатию и растяжению (m=σпчр/σпчс). Для пластичных материалов m=1, и при этом гипотеза Мора сводится к третьей гипотезе. [4] §3 Усталость и выносливость материалов при циклических нагрузках 3.1. Понятия усталости и выносливости Многие детали машин и механизмов, а также конструкции сооружений в процессе эксплуатации подвергаются циклически изменяющимся во времени воздействиям. Если уровень напряжений, вызванный этими воздействиями, превышает определенный предел, то в материале формируются необратимые процессы накопления повреждений, которые в конечном итоге приводят к разрушению системы. Процесс постепенного накопления повреждений в материале под действием переменных напряжений, приводящих к разрушению, называется усталостью. Свойство материала противостоять усталости называется выносливостью. Опыт показывает, что при переменных напряжениях после некоторого числа циклов может наступить разрушение детали, в то время как при том же неизменном во времени напряжении Число циклов до момента разрушения зависит от величины  Рис. 7 3.2. Основные характеристики цикла Рассмотрим вначале случай одноосного напряженного состояния. Закон изменения главного напряжения во времени представлен кривой, показанной на рис.8.  Рис. 8 Н В случае, когда 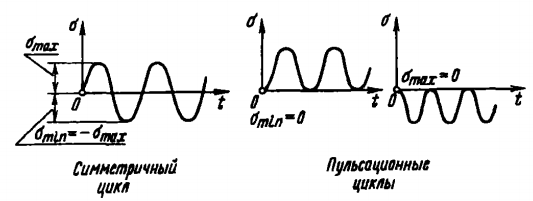 Рис.9 Любой цикл может быть представлен как результат наложения постоянного напряжения Т т.е. Путем многократных испытаний (если имеется достаточное количество образцов) можно определить число циклов, которое выдерживает образец до разрушения, в зависимости от величины  Рис.10 3.3 Предел выносливости Опыт показывает, что для большинства черных металлов можно указать такое наибольшее максимальное напряжение, при котором материал не разрушается при любом числе циклов. Такое напряжение называется пределом усталости или пределом выносливости. Предел выносливости – такое максимальное напряжение цикла, при котором образец не разрушается до базы испытания, где R – коэффициент асимметрии цикла. База испытания – число циклов, до которого ведут испытание. Предел выносливости обозначается через Определение предела выносливости является трудоемкой операцией, поэтому был сделан ряд попыток связать эмпирическими формулами предел выносливости с известными механическими характеристиками материала. Обычно считается, что для сталей предел выносливости при изгибе составляет половину от предела прочности: Для высокопрочных сталей можно принять: Для цветных металлов предел выносливости изменяется в более широких пределах: Аналогично испытанию на чистый изгиб можно вести испытание на кручение в условиях циклически изменяющихся напряжений. В этом случае: или для обычных сталей берется Указанные соотношения и все им подобные следует, однако, применять с большой осторожностью, поскольку они получены только для определенных материалов и в определенных условиях испытаний (при изгибе, при кручении) [5]. 3.4 Диаграмма усталостной прочности Положим, имеется машина, на которой можно производить усталостные испытания в условиях любого несимметричного цикла. Задавая постоянное значение Продолжая такие испытания и дальше, получаем множество точек, через которые проводится предельная кривая, характеризующая прочностные свойства материала в условиях несимметричных циклов. Эта кривая носит название диаграммы усталостной прочности (рис.11). 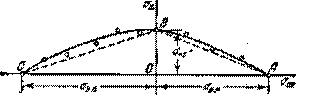 Рис.11. Диаграмма усталостной прочности. Точки А и С диаграммы соответствуют пределам прочности при простом растяжении и сжатии. Точка В отражает результаты испытания в условиях симметричного цикла. Полученная диаграмма дает возможность судить о прочности конструкции, работающей при циклически изменяющихся напряжениях. Положим, для некоторой детали цикл характеризуется значениями напряжений 4. Расчет вала на изгиб с кручением Для ведущего вала прямозубой цилиндрической передачи редуктора с двумя зубчатыми колесами (рис.12, а), передающего мощность P = 3 кВт, при угловой скорости  = 25 рад/с: = 25 рад/с:Определить вертикальные и горизонтальные составляющие реакций подшипников. Построить эпюру крутящих моментов. Построить эпюры изгибающих моментов в вертикальной и горизонтальной плоскостях. Определить диаметр вала по третьей гипотезе прочности (гипотеза наибольших касательных напряжений), полагая: Fr1 = 0,4F1; Fr2 = 0,4F1. Принять: нормативный коэффициент запаса прочности [n] = 1,8, марка стали – СТ10. Поверхность вала полированная (Ra = 1) [2]. Решение: 1. Составляем расчетную схему вала, приводя действующие на вал нагрузки к оси (рис.12, б). При равномерном вращении вала М1 = М2, где М1 и М2 — скручивающие пары, которые добавляются при переносе сил F1 и F2 на ось вала. 2. Определяем вращающий момент, действующий на вал: 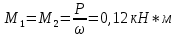 . .3. Вычислим нагрузки, приложенные к валу: 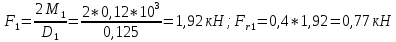 ; ;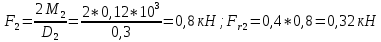 . .Р 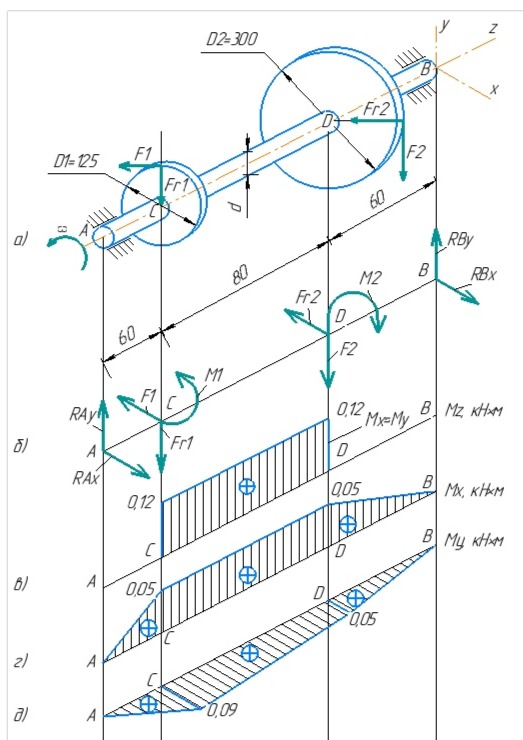 ис. 12 Эпюры усилий и моментов вала ис. 12 Эпюры усилий и моментов вала4. Определяем реакции опор в вертикальной плоскости (рис.12, б): 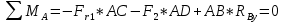 ; ;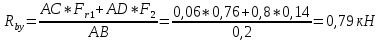 ; ;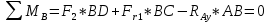 ; ;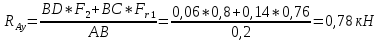 . .Проверим: 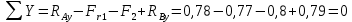 , ,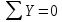 , следовательно, реакции опор были найдены правильно. , следовательно, реакции опор были найдены правильно.Определяем реакции опор в горизонтальной плоскости (рис. , б): 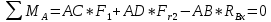 ; ;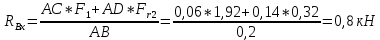 ; ;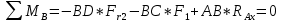 ; ;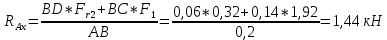 . .Проверим: 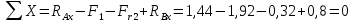 , ,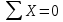 , следовательно, реакции опор были найдены правильно. , следовательно, реакции опор были найдены правильно.5. Строим эпюру крутящих моментов Mz (рис.12, в). 6. Определяем в характерных сечениях значения изгибающих моментов Mx в вертикальной плоскости и My в горизонтальной плоскости и строим эпюры (рис.12, г, д): 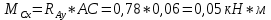 ; ;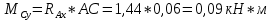 . .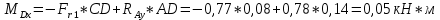 ; ;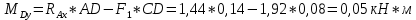 ; ;7. Определяем наибольшее значение эквивалентного момента по третьей гипотезе прочности (гипотеза касательных напряжений). Так как суммарное значение изгибающего момента в сечении C больше, чем в сечении B: 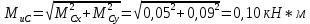 , ,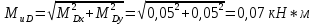 , ,то сечение C и является опасным. Определяем эквивалентный момент в сечении C по третьей гипотезе прочности: 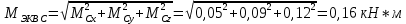 . .8. Вычисляем нормальное допускаемое напряжение: 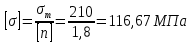 . .9. Определяем требуемые размеры вала: 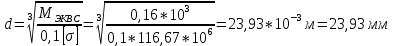 . .Принимаем dвала= 24 мм. [7]. Расчет вала на сопротивление многоцикловой усталости Изменить расчетную схему, считая, что вал ступенчатый. Все остальные параметры оставить без изменения. Принять: сталь – СТ10, качество обработки поверхности – 1 (полирование). Радиус галтели ρ в переходных сечениях от большого диаметра D к малому диаметру d принять равным 0,5(D - d). 1. Определить диаметры вала из условия статической прочности в указанных сечениях и спроектировать ступенчатый вал, округлив диаметры ступеней до стандартного размера. 2. Определить фактический запас прочности вала при циклических нагрузках. 3. Рассчитать запас прочности по нормальным напряжениям с учетом усталости в опасных сечениях, считая концентраторами напряжений уступ с галтелью и шпоночный паз, необходимый для закрепления на валу шкивов с помощью шпонок. Цикл нормальных напряжений симметричный. 4. Проделать такой же расчет для определения запасов прочности по касательным напряжениям. Цикл касательных напряжений считать пульсирующим. 5. Рассчитать полный запас прочности с учетом усталости материала. 6. При получении коэффициента запаса усталостной прочности меньше допустимой величины [n]=1,8 предложить конкретные меры повышения усталости прочности: а) – конструктивные приемы, связанные с изменением формы опасных участков вала, б) – меры технологического упрочнения [6]. Решение: Определяем требуемые размеры вала на участках AС, СD и DB. Допускаемые напряжения при действии знакопеременных нагрузок значительно ниже, чем в случае статической нагрузки (примерно в 1,9). Для СТ10 примем [σ]р = 60 МПа [ССЫЛКА В ВК 4]. I участок AC: 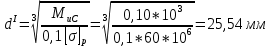 . . Принимаем 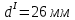 . [7]. . [7].II участок CD: 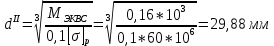 . . Принимаем 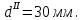 [7]. [7].III участок DB: 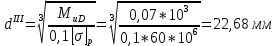 . . Принимаем 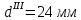 . [7]. . [7].На II участке CD диаметр рассчитан в I части курсовой работы: 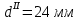 . .2. Определение геометрических характеристик вала: 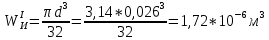 ; ;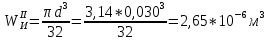 ; ;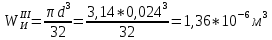 ; ;с учетом ослабления пазами для двух стандартных шпонок [табл. 3 приложения 6] 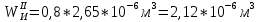 . .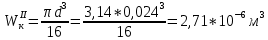 ; ;с учетом ослабления пазами для двух стандартных шпонок [табл. 3 приложения 6] 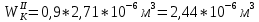 . .Вычисляем номинальные напряжения: 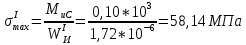 ; ;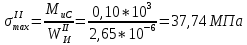 ; ;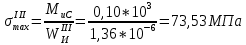 ; ;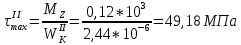 . .Вычисляем амплитуды и средние напряжения цикла: I. 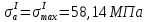 ; ; 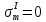 . .II. 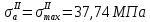 ; ; 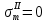 ; ;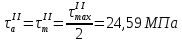 . . III. 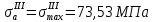 ; ; 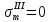 ; ; 3. Определяем радиусы галтелей: 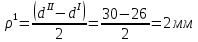 . .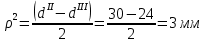 . .4. Определяем коэффициенты концентрации напряжений: При 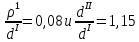 по графику на рисунке 13 имеем: по графику на рисунке 13 имеем: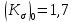 . .При 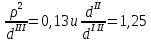 по графику на рисунке 13 имеем: по графику на рисунке 13 имеем: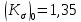 . .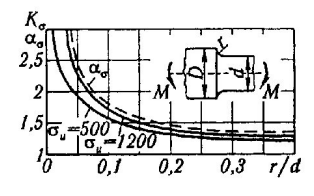 Рис.13 – эффективные коэффициенты концентрации при изгибе для ступенчатых валов с отношением D/d=2, с переходом по круговой галтели радиуса r Учитывая, что в нашем случае D/d = 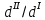 =1,15 и =1,15 и 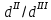 =1,25, используя график на рис. 14, находим поправочные коэффициенты =0,75 (для изгиба, участок I) =86 (для изгиба, участок III). =1,25, используя график на рис. 14, находим поправочные коэффициенты =0,75 (для изгиба, участок I) =86 (для изгиба, участок III).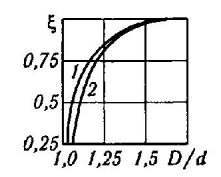 Рис.16 – поправочные коэффициенты при изгибе (кривая 1) и кручении (кривая 2) Находим эффективные коэффициенты концентрации напряжений по формулам: 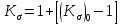 ; ;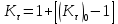 . .где 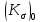 и и 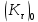 – коэффициенты концентрации напряжений при D/d=2. – коэффициенты концентрации напряжений при D/d=2.I. 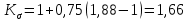 . .II. 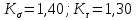 [по табл.3 в приложении 6] [по табл.3 в приложении 6]III. 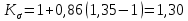 . .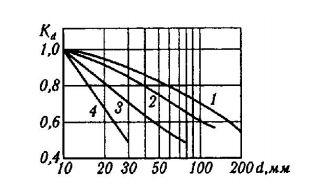 Рис. 17 — коэффициенты влияния абсолютных размеров Kd 1 — детали из углеродистой стали без концентратора, 2 — детали из легированной стали при отсутствии концентратора и из углеродистой стали при наличии концентратора, 3 — детали из легированной стали при наличии концентратора, 4 — для любой стали при весьма большой концентрации напряжений Находим коэффициенты влияния абсолютных размеров для вала: dI = 26 мм, по рис. 17 (кривая 2) Кd = 0,88. dII = 30 мм, по рис. 17 (кривая 2) Кd = 0,85. Приближенно принимаем Кdτ = Кd = 0,85. dIII = 24 мм, по рис. 17 (кривая 2) Кd = 0,90. Поверхность вала полированная, поэтому KF = 0,98. Определяем коэффициенты чувствительности материала к асимметрии цикла ψσ и ψτ [по табл. 2, приложения 6]. Для СТ10 σB = 340 МПа, тогда ψσ = 0,05 , ψτ = 0,03. 5. Вычисляем коэффициенты запаса прочности. По пределу выносливости: 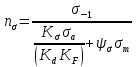 ; ; 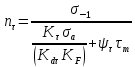 I. 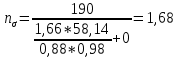 . .II. 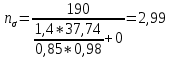 ; ;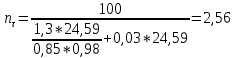 ; ;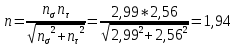 . .III. 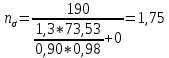 ; ;По пределу текучести: 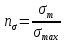 ; ; 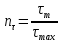 . .I. 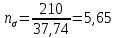 . .II. 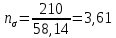 ; ;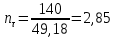 ; ;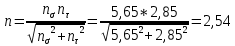 . .III. 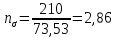 . .Запасы прочности по пределу выносливости сравним с нормативным коэффициентом запаса прочности [n] = 1,8. Фактические запасы прочности на участках AC и DB значительно меньше нормативного, поэтому необходимо, например: -увеличить диаметры ступеней вала, определив их из расчета на выносливость -применить более прочную сталь -улучшить качество обработки поверхности [6]. Выводы Как показывает анализ причин отказов технических систем, более чем в 70% случаев, разрушения связаны с усталостным повреждением элементов машин, оборудования и сооружений [1]. Такое положение объясняют спецификой явления многоцикловой усталости, в частности: - зарождением и развитием трещин при относительно низких напряжениях; -чувствительностью к различным конструкторским, технологическим факторам; -значительным рассеянием характеристик выносливости по сравнению с характеристиками статической прочности; - локальным и избирательным характером зарождения трещин и их развитием без проявления видимых остаточных перемещений вплоть до момента 18 возникновения аварийных ситуаций. Поэтому актуальной становится проблема предотвращения усталостных разрушений ответственных деталей. 7. Список литературы [Интернет-источник]- http://сопроматт.рф/Theory/Theory-9.html [Интернет-источник] -http://www.soprotmat.ru/sloz.htm#_Изгиб_с_растяжением Конспект лекций по сопротивлению материалов — ПНИПУ. — Пермь, 2020. Гипотезы прочности [Интернет-источник] - https://sopromato.ru/gipotezi-prochnost/gipotezi-prochnosti [Интернет-источник] - http://www.soprotmat.ru/kolebania.htm Методические указания к выполнению курсовой работы по дисциплине «Сопротивление материалов» для студентов специалитета по направлению 24.05.02 «Проектирование авиационных и ракетных двигателей» / сост. Е.Ю. Макарова. – Пермь : Изд-во Перм. нац. исслед. политехн. ун-та, 2017. – 25 с. ГОСТ 6636—69 Стандартные диаметры вала. ГОСТ 7.32-2001 Отчет о научно-исследовательской работе. Структура и правила оформления». |