Отчеты оформляются в виде файлов формата Microsoft Word (файлы других форматов не принимаются), размер шрифта 1214

• Название: Отчеты оформляются в виде файлов формата Microsoft Word (файлы других форматов не принимаются), размер шрифта 1214
• Дата: 06.04.2023
• Размер: 452.53 Kb.
• Имя файла: LabJob23.docx
• Тип: Отчет; #1041909
• страница: 2 из 12

Лабораторная/практическая работа № 2

1. 
   Название работы: «Лексика языков программирования. Конечные автоматы без памяти для обнаружения слов в тексте программы».
   
2. 
   Цели работы: изучение конечных автоматов (КА) без памяти, способов определения КА в трансляторах – графового и табличного, методов построения недетерминированного КА по системе регулярных выражений, методов эквивалентных преобразований недетерминированных КА в оптимальные полностью определенные КА – лексические акцепторы.
   
3. 
   Основные теоретические сведения:
   

1. 
   Конечные автоматы без памяти
   

Конечный автомат без памяти есть совокупность

K = {A, C, С₀, G, F},

где A – алфавит входных символов; C – конечное множество состояний; С₀ – начальное состояние; G – функция переходов, которая по текущему состоянию автомата и входному символу формирует его состояние в следующий момент времени; F – конечное множество состояний останова (финальных состояний).

Применительно к программной реализации в трансляторах конечным автоматом без памяти называется математическая модель устройства, которое:

• 
  имеет определенный набор рабочих состояний C, среди которых выделено особое начальное (стартовое) состояние С₀ и некоторый набор состояний останова (финальных состояний)F;
  
• 
  имеет один вход и не имеет ни одного выхода;
  
• 
  в любой момент времени на входе имеет либо в точности один символ входного алфавита A, либо пустую цепочку ε;
  
• 
  функционирует в дискретном времени t₀, t₁, t₂, ...;
  
• 
  при запуске, т. е. в момент времени t₀, всегда оказывается в начальном состоянии С₀, на входе в этот момент находится самый первый символ входной цепочки;
  
• 
  в любой момент времени t_i по текущему состоянию и символу, находящемуся на входе, в соответствии с функцией G определяет номер рабочего или финального состояния, в котором автомат окажется в момент времени t_i+1;
  
• 
  если по каким-либо причинам номер следующего состояния не может быть определен, то автомат останавливается по ошибке (для остановов по ошибке подразумевается существование особого финального состояния, не принадлежащего множеству F);
  
• 
  при любом переходе в рабочее состояние или состояние останова по ошибке текущий входной символ заменяется следующим символом из входной цепочки;
  
• 
  при переходе в финальное состояние обнаружения правильного слова входной символ автомата не изменяется (такой переход выполняется по пустой цепочке ε; действия со входным символом при переходе по пустой цепочке состоят в чтении символа со входа + обнаружении того, что символ не принадлежит текущему слову + возврате этого символа на вход автомата);
  
• 
  каждому финальному состоянию, не являющемуся состоянием останова по ошибке, поставлена в соответствие группа правильных слов, возможно, не единственная; останов автомата в таком состоянии понимается как обнаружение им правильного слова этой группы (или слова, принадлежащего нескольким группам).
  

Пусть требуется решить задачу распознавания двоичных чисел, разделенных последовательностями пробелов. Простая система регулярных определений может описать слова этих двух групп:

BinaryNumber : [01] +

Space : [ ] +

Существует как минимум три способа определения конечного автомата без памяти, способного распознавать такие слова.

1. 
   Конечный автомат без памяти может быть задан только функцией переходов, если соблюдаются определенные соглашения о способе нумерации состояний (начальным является состояние номер 0):
   

{текущее состояние; входной символ; следующее состояние}

Пример такого определения автомата:

{0,ε,-1} {0,\d32,1} {0,0,2} {0,1,2} {1,\d32,1} {1, ε,-2} {2,0,2} {2,1,2} {2,ε,-3}

Алфавит входных символов может быть извлечен из функции переходов, это символы 0, 1, пробел (символ с десятичным кодом \d32). Любые другие символы, которые могут появиться на входе автомата, здесь обозначены пустой цепочкой ε, их обработка состоит в переходе автомата в финальные состояния.

Состояния 0, 1 и 2 являются рабочими, поскольку для них определены переходы в другие состояния по входным символам. Состояния -1, -2 и -3 – финальные, поскольку из них не существует ни одного перехода. Состояние -1 соответствует обнаружению конца цепочки символов, содержащей только правильные слова, т.е. двоичные числа и последовательности пробелов. Останов автомата в состоянии -2 означает обнаружение последовательности пробелов, а в состоянии -3 – обнаружение двоичного числа.

При программной реализации конечные автоматы без памяти обычно представляются либо графами состояний и переходов, либо управляющими таблицами.

2. 
   Графом состояний и переходов (ГСП) конечного автомата без памяти (далее просто конечного автомата - КА) называется помеченный ориентированный граф, вершины которого сопоставлены состояниям, а дуги – переходам.
   

Разметка вершин обычно производится целыми числами, обозначающими номера состояний. Имеется особая начальная вершина (имеющая обычно номер 0), в которую не входит ни одна дуга. Дуги графа могут быть помечены обозначением пустой цепочки ε, одиночным символом, перечнем или диапазоном символов.

Существуют особые финальные вершины, из которых не может выходить ни одна дуга. Имеется одна или несколько рабочих вершин, в которые могут входить дуги и из которых могут выходить дуги.

Пример списка состояний и переходов конечного автомата,распознающего двоичные числа и последовательности пробелов в представлении, формируемом ВебТрансБилдером:

0:		EOF-> -1 [\d32] -> 1 [01]-> 2
1:		[other]-> -2 [\d32] -> 1
2:		[other]-> -3 [01]-> 2

Разметка дуг графа производится с помощью указания одного из символов входного алфавита того языка, для распознавания слов которого построен данный автомат либо обозначения пустой цепочки символов ε, которому здесь соответствует [other]. Это обозначение надо понимать так: любой символ, не принадлежащий разметке какой-либо дуги, выходящей из данного состояния. Поэтому в разных состояниях [other] обозначают разные множества символов. Для состояния 1 это не пробел, а для состояния 2 – любой символ кроме двоичных цифр. Если дуга помечена символом входного алфавита, то при переходе по этой дуге автомат заменяет данный входной символ следующим символом из входной цепочки. При переходе по дуге, помеченной обозначением пустой цепочки ε, символ на входе автомата не изменяется.

3. 
   Еще одним способом определения конечного автомата без памяти является табличный способ. Автомат задается прямоугольной таблицей, строки которой обычно соответствуют состояниям, а столбцы – входным символам. Номера состояний и входные символы показаны в заголовках строк и столбцов, однако следует помнить, что заголовки строк и столбцов не являются элементами таблицы. В клетках таблицы указываются номера состояний перехода (из состояния, в строке которого находится клетка по символу, указанному в заголовке столбца). Пример управляющей таблицы (УТ) автомата, предназначенного для акцепта двоичных чисел, формируемой пакетом ВебТрансБилдер показан в табл. 2.1.
   

Таблица 2.1

	0	1	2
[ ► ]	-1	-2	-3
[ \d32 ]	1	1	-3
[ 01 ]	2	-2	2

Так называемая рабочая зона управляющей таблицы содержит только клетки с переходами (верхняя строка показанной таблицы не входит в рабочую зону). Если в рабочей зоне управляющей таблицы нет пустых клеток, то автомат называется полностью определенным. В противном случае автомат называется не полностью определенным.

2. 
   Понятие истории работы конечного автомата
   

Историей работы конечного автомата без памяти для данной входной цепочки называется упорядоченная (по моменту дискретного времени, т.е. номеру шага) совокупность троек значений {t,a,c}, где t – момент дискретного времени; a – текущий входной символ; c – текущее состояние. Для любой конечной по количеству символов входной цепочки автомат, запущенный в начальном состоянии, завершит свою работу за конечное число шагов, т. е. реализует конечную историю работы.

Историю работы автомата удобно представлять в виде таблицы, столбцы которой содержат значения троек. В качестве момента времени t _i указывается порядковый номер iтакта работы автомата.

Пусть дана входная цепочка 101 10, тогда история работы автомата будет выглядеть так (табл. 2.2.):

Таблица 2.2.

Такт	0	1	2	3	4	5	6	7	8	9	10	11	12	13
Символ	1	0	1	\d32		\d32	1		1	0	►		►
Состояние	0	2	2	2	-3	0	1	-2	0	2	2	-3	0	-1

Остановы автомата в состоянии -3 свидетельствуют об обнаружении двоичных чисел, в состоянии -2 – об обнаружении последовательности пробелов, в состоянии -1 – об обнаружении конца входной цепочки.

Конечный автомат, заданный вышеприведенными графом или таблицей, для любой конкретной входной цепочки при каждом запуске будут реализовывать одну и ту же историю работы.

Такие автоматы называются детерминированными.

3. 
   Детерминированность и недетерминированность
   

Однако существуют и недетерминированные автоматы, которые могут отрабатывать разные последовательности переходов из состояния в состояние при различных запусках для одной и той же входной цепочки символов. Такие автоматы играют важную роль в процессе преобразования систем регулярных определений в детерминированный конечный автомат, поэтому необходимо рассмотреть причины возникновения недетерминированности. Есть два рода (причины) недетерминированного поведения конечных автоматов.

Недетерминированностью первого рода называется наличие хотя бы одного перехода по пустой цепочке символов ε в рабочее состояние. Простой пример совокупности состояний и переходов фрагмента автомата с такой недетерминированностью, формируемый ВебТрансБидером:

0:		[other] -> 2 [–+] -> 1
1:		[other] -> 2 [0-9] -> 3
2:		[0-9] -> 3
3:		[other] -> -2 [0-9] -> 3

Этот фрагмент получен в результате выполнения первого шага преобразования [2] формального определения десятичных констант в экспоненциальной форме, содержащих показатель со знаком или без знака:

Const : [0-9]+([.][0-9]*([-+]?[eE][0-9]+)?)?

Другие формы представления этого фрагмента (он не является полностью определенным в силу того, что в управляющей таблице есть пустые клетки) показаны на рис. 2.1.: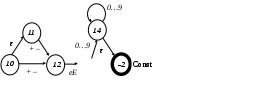







13

Рис. 2.1. Фрагменты графа состояний и УТ
Автомат, содержащий этот фрагмент, в отличие от детерминированных автоматов, при разных запусках для одной и той же входной цепочки символов может реализовывать разные истории работы. Если он находится в состоянии 10 и на входе один из символов + или –, то возможна два разных продолжения истории работы: либо переход в состояние 12 по + или –, либо переход в состояние 11 по пустой цепочке, а затем в состояние 12 по + или –.

Реализуя разные истории работы, этот автомат тем не менеекаждой входной цепочке ставит в соответствие всегда одно и то же финальное состояние.

Недетерминированностью второго рода называется наличие в управляющей таблице клеток, содержащих два или более номера состояния (или столбцов, помеченных одним и тем же символом, но не являющихся идентичными).

В графе состояний и переходов это соответствует дугам, выходящим из одной вершины, помеченным одним и тем же символом, но ведущим в разные вершины. Недетерминированность второго рода, так же, как и первого, порождает возможность реализации нескольких различных историй работы автомата для одной и той же входной цепочки при разных запусках.Пример автомата, с недетерминированностью второго рода, показан на рис. 2.2.




Рис. 2.2. Автомат с недетерминированностью второго рода

В управляющей таблице этого автомата есть клетки, содержащие несколько разных номеров состояний.

Недетерминированность состоит в том, что автомат, оказавшись в состоянии номер 2, может перейти по любому из символов 0 или 1 как в состояние 1, так и в состояние 3.

Несмотря на то что поведение автомата при разных запусках для одной и той же входной цепочки может быть различным, его финальное состояние для любой цепочки будет одним и тем же независимо от того, какая история работы была им реализована.

Недетерминированность автомата как первого, так и второго рода, может возникнуть в результате его построения формальными методами путем преобразования описания лексики языка.

Кроме того, недетерминированность одного рода может возникнуть в процессе эквивалентных преобразований автомата при ликвидации недетерминированности другого рода.

4. 
   Недостижимые, тупиковые и эквивалентные состояния
   

На рис. 2.3 показан граф состояний автомата, содержащего недостижимые, тупиковые и эквивалентные состояния. Автомат имеет два тупиковых состояния с номерами 2 и 3, три недостижимых состояния с номерами 6, 7 и 8 и эквивалентные состояния 4 и 5.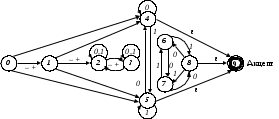




Рис. 2.3. Недостижимые, тупиковые и эквивалентные состояния

Недостижимым называется такое состояние автомата, в которое не
существует ни одного пути из начального состояния.

Тупиковым называется состояние, из которого не существует ни одного пути в какое-либо финальное состояние акцепта.

Как тупиковые, так и недостижимые состояния могут быть удалены из автомата вместе со всеми своими (как входящими, так и выходящими) дугами переходов, в результате будет получен автомат, эквивалентный исходному.

Эквивалентными называются такие два состояния, для которых строки в управляющей таблице либо полностью совпадают, либо различаются только переходами друг на друга. Любую пару эквивалентных состояний всегда можно заменить одним состоянием без потери функциональности автомата.

5. 
   Оптимальность конечных автоматов без памяти
   

Оптимальным в множестве эквивалентных друг другу автоматов называется полностью определенный детерминированный автомат, управляющая таблица которого имеет минимальное количество клеток в рабочей зоне.

Оптимальный автомат удовлетворяет следующим критериям:

1. 
   Множества символов, помечающие столбцы управляющей таблицы, попарно не пересекаются.
   
2. 
   Автомат не содержит недетерминированностей первого рода.
   
3. 
   Автомат не содержит недетерминированностей второго рода.
   
4. 
   Автомат не имеет тупиковых состояний.
   
5. 
   Автомат не имеет недостижимых состояний.
   
6. 
   Все рабочие состояния попарно не являются эквивалентными.
   
7. 
   В рабочей зоне управляющей таблице нет одинаковых столбцов.
   
8. 
   В рабочей зоне управляющей таблицы нет пустых клеток.
   

Любой конечный автомат без памяти, не удовлетворяющий хотя бы одному из этих критериев, может быть преобразован в эквивалентный ему оптимальный автомат. Методы и алгоритмы такого преобразования подробно рассматриваются в [1,2], результаты преобразования разработанной студентом системы правил должны быть изучены в этой работе.

4. 
   Порядок выполнения работы (рекомендуется использовать в качестве примера систему правил Samples/Sample2):
   

1. 
   Используя пакет ВебТрансБилдер, освоить:
   

• 
  создание лексических правил на языке регулярных выражений (РВ);
  
• 
  построения сложных регулярных выражений с использованием способа определения любого символа в виде «[]», квантификаторов вида {<число>,<число>} и операций выбора «|» языка РВ;
  

2. 
   Разработать (доработать разработанный при выполнении работы №1) систему правил для всех групп слов языка, определенного заданием на курсовую работу (в том числе комментариев, которые заданием не определены, но в программах на любом языке необходимы). Построить по этой системе:
   

• 
  сканер, управляемый графом состояний и переходов;
  
• 
  сканер, управляемый таблично.
  

3. 
   Изучить структуру программных модулей, построенных ВебТрансБилдером, используя операцию меню «Показать/Код транслятора», найти и изучить в этих кодах функции лексического акцепта для графового и табличного способов реализации КА, сравнить реализации конечных автоматов, управляемых различными способами. Изучить по программному коду способ реализации вызова действий, определенных в лексических правилах и алгоритм работы формирователя лексем.
   
4. 
   Проверить функционирование конечных автоматов, построенных ВебТрансБилдером:
   

• 
  подготовить тестовый пример программы на языке, заданном на курсовую работу (пример должен содержать слова абсолютно всех групп языка);
  
• 
  запустить каждый автомат на выполнение, протрассировать с использованием отладчика браузера (для открытия отладчика нажать функциональную клавишу F12) вручную работу лексического акцептора и в графовой и в табличной реализации. Для этого расставить точки останова в лексическом акцепторе и лексическом анализаторе (функции getLexem, имеющиеся и в акцепторе, и в анализаторе) и проследить процессы лексического акцепта и анализа тестовой программы (программа должна содержать несколько слов из групп «идентификаторы», «константы» и «пробелы»);
  
• 
  убедиться в работоспособности автоматов, в противном случае – доработать систему РВ и добиться правильности функционирования лексического акцептора.
  

5. 
   Построить вручную в виде двух таблиц из трех строк каждая две истории работы табличного и графового автоматов как результаты обработки ими последовательностей символов, образующих два различных оператора присваивания языка, заданного на курсовую работу.
   

Строки таблиц должны содержать:
1. Номер шага.
2. Текущий входной символ.
3. Текущее состояние автомата.

Сравнить последовательности обнаруженных слов в построенных историях работы с теми, которые формируются при тестировании сканера, объяснить расхождения, если они имеются.

6. 
   Разработать полное описание лексики учебного языка, заданного на курсовое проектирование в качестве заготовки фрагмента расчетно-пояснительной записки к курсовой работе. Описание лексики должно включать все группы слов языка. Для каждой группы должны быть сформулированы:
   

- назначение (или способы использования) слов этой группы в программах на учебном языке;

- правила формирования слов языка из символов алфавита (или перечень допустимых слов);

- характеристики слов, если они имеют значение для синтаксического и семантического анализа (например – приоритеты знаков операций, диапазоны значений констант);

- примеры правильных слов.

7. 
   Подготовить, сдать и защитить отчет к лабораторной работе.
   

5. 
   Требования к содержанию отчета.
   

Отчет должен содержать:

• 
  цель работы;
  
• 
  доработанную систему правил, определяющую полностью все группы слов языка, заданного на курсовую работу;
  
• 
  управляющую таблицу и граф состояний и переходов сканеров, построенных ВебТрансБилдером по этой системе, краткое описание алгоритмов функционирования этих автоматов; результаты отладочной трассировки сканеров;
  
• 
  две истории работы табличного и графового лексических автоматов, построенные путем ручной имитации работы автоматов при лексическом анализе двух различных оператора присваивания языка, заданного на курсовую работу;
  
• 
  описание лексики учебного языка, определенного заданием на курсовую работу;
  
• 
  выводы и заключение;
  
• 
  приложение – тестовая программа на языке, заданном на курсовую работу, содержащая все элементы языка (функции, блоки операторов и все управляющие операторы, т.е. условные, циклы, переключатели, присваивания и все виды констант).
  

6. 
   Контрольные вопросы.
   

1. 
   Что такое конечный автомат без памяти?
   
2. 
   Какие существуют способы задания конечных автоматов без памяти?
   
3. 
   Что такое первичное регулярное выражение?
   
4. 
   Как можно задать перечень и диапазон символов в регулярном выражении?
   
5. 
   Что такое квантификаторы, какие квантификаторы можно использовать в системах правил для пакета ВебТрансБилдер?
   
6. 
   Что такое эквивалентность конечных автоматов без памяти?
   
7. 
   Что такое тупиковые, недостижимые и эквивалентные состояния конечного автомата без памяти?
   
8. 
   Что такое оптимальность конечного автомата?
   
9. 
   Перечислите основные этапы процесса преобразования системы регулярных выражений в конечный автомат без памяти.
   
10. 
    Что такое недетерминированность конечного автомата без памяти? Перечислите виды недетерминированности.
    
11. 
    Что такое полностью и неполностью определенные конечные автоматы без памяти?
    
12. 
    Опишите существо процесса эпсилон-замыкания множества вершин графа состояний и переходов при ликвидации недетерминированностей.
    
13. 
    Какие способы преобразования графа состояний и переходов соответствуют операциям языка регулярных выражений?
    
14. 
    Как осуществляется поиск и удаление тупиковых состояний конечного автомата без памяти?
    
15. 
    Как осуществляется поиск и удаление недостижимых состояний конечного автомата без памяти?
    
16. 
    Как осуществляется поиск и слияние эквивалентных состояний конечного автомата без памяти?
    
17. 
    Как осуществляется преобразование не полностью определенного конечного автомата без памяти в полностью определенный?
    
18. 
    Что такое рабочая зона управляющей таблицы конечного автомата без памяти?
    
19. 
    Что такое история работы управляющей таблицы конечного автомата без памяти?
    
20. 
    Как в метаязыке регулярных выражений определяются символы, не имеющие графического изображения?