Отчеты оформляются в виде файлов формата Microsoft Word (файлы других форматов не принимаются), размер шрифта 1214
 Скачать 452.53 Kb. Скачать 452.53 Kb.
|
Лабораторная/практическая работа № 5Название работы: «Синтаксис языков программирования. Восходящий синтаксический анализ, автоматная реализация». Цели работы: изучение основных идей и понятий восходящего синтаксического анализа, свойств формальных грамматик, определяющих принадлежность грамматики к одному из классов LR, получение навыков построения автоматной реализации восходящего анализатора, исследование поведения восходящих синтаксических акцепторов. Основные теоретические сведения: Восходящие методы синтаксического анализа Восходящими называются такие методы синтаксического анализа, при которых цепочка терминальных символов входного предложения шаг за шагом «сворачивается» в цепочки, содержащие и нетерминальные символы и являющиеся очередными уровнями дерева грамматического разбора. Этот процесс продолжается до тех пор, пока все правильное предложение не окажется свернутым в цепочку, содержащую единственный нетерминальный символ – начальный нетерминал грамматики, либо до тех пор, пока не будет обнаружена невозможность восстановления дерева для неправильных предложений, т. е. ошибка Как и для группы нисходящих методов, главным прагматическим требованием к организации процесса сворачивания цепочек является детерминированность (однонаправленность) движения по дереву снизу вверх. Опять-таки, как и при нисходящем анализе, не любая грамматика обладает такими свойствами, чтобы по ее правилам можно было осуществлять детерминированное восходящее восстановление дерева разбора. Структура автомата для восходящего восстановления дерева грамматического разбора Восходящий синтаксический акцептор представляет собой конечный автомат со стековой памятью (рис. 5.1.), управляемый входным символом и текущим состоянием. 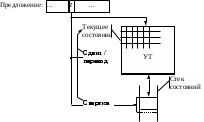 Рис. 5.1.Восходящий парсер как автомат с несколькими состояниями и стеком состояний Перед запуском автомата номер его начального состояния (состоянии с номером 0) должен быть занесен в стек. Далее на каждом шаге работы номер состояния, находящий на верхушке стека, используется в качестве текущего и определяет выбор строки управляющей таблицы. Из входного предложения прочитан первый терминал, этот символ находится на входе автомата и определяет колонку управляющей таблицы. На каждом шаге работы из клетки, находящейся на пересечении строки текущего состояния и столбца текущего символа выбирается и выполняется знак операции, в результате чего может измениться содержимое стека (и, соответственно, текущее состояние) и символ на входе автомата. Этот процесс продолжается до тех пор, пока автомат не остановится по завершению восстановления дерева разбора правильного предложения или по обнаружению ошибки. Знаки операций, которые могут находиться в клетках управляющей таблицы, таковы: Sn – сдвиг (Shift) по входному предложению, т.е. чтение следующего терминала из анализируемого предложения путем вызова лексического анализатора, сопровождаемое занесением номера состояния n на верхушку стека. Автомат переключается в состояние n, на его входе появляется прочитанный терминал. Gn – переход (Go) в новое состояние. Номер состояния n заносится на верхушку стека, автомат переключается в состояние n. Эта операция выполняется всегда после выполнения операции свертки, которая «образовала» нетерминальный символ и поместила его на вход автомата перед текущим терминалом. Текущий терминал не изменяется. Rk,N – свертка (Reduce) правой части правила для нетерминала N, имеющей длину k символов. С верхушки стека сбрасывается в никуда k номеров состояний (эта последовательность номеров образовалась в стеке в результате выполнения k предыдущих во времени операций Shift и Go, соответствующих символам правой части этого правила). Автомат переключается в состояние, номер которого остался на верхушке стека (и который был там до выполнения k операций Shift и Go, соответствующих символам правой части этого правила). Формируется нетерминал N, временно, до выполнения операции Go, «вытесняющий» текущий терминал со входа автомата. В дальнейшем для удобства практической реализации вместо обозначения Rk,N будет использоваться обозначение Rk,n, где малое n обозначает номер столбца управляющей таблицы, помеченного нетерминалом N. Stop – останов по завершению восстановления дерева разбора правильного предложения (пакет ВебТрансБилдер вместо этого обозначения формирует знак операции S-1; отрицательное значение в обозначении операции Shift трактуется как операция Stop). Отсутствие любой из этих операций в клетке означает операцию останова по обнаружению ошибки. Для преобразования данной контекстно-свободной грамматики в управляющую таблицу такого автомата может быть использовано несколько разных по сложности алгоритмов. В процессе преобразования может быть выяснено, применим ли данный алгоритм к данной грамматике, т.е. будет ли построенный автомат стопроцентно работоспособен. При получении положительного ответа на этот вопрос можно просто использовать построенный автомат следует т в качестве парсера. При обнаружении отрицательного результата можно попытаться построить автомат, применяя более сложный алгоритм, или же попытаться модифицировать грамматику или ее свойства для повторного применения уже использовавшегося алгоритма. Алгоритмы преобразования используют то или иное понятие конфигурации. Начнем с простейшего. Понятие конфигурации. Связь между конфигурациями, состояниями и операциями восходящего парсера Для иллюстрации процессов, протекающих при построении восходящего парсера, будем использовать грамматику языка арифметических выражений G a1 с добавленным специальным правилом вида Z : S ► (табл. 5.1.)  Таблица 5.1.
Под конфигурацией понимается правило грамматики, в котором в произвольной точке правой части помещен дополнительный метасимвол – маркер. Маркером отмечается возможное разбиение правой части правила в процессе восходящего синтаксического анализа на две цепочки: «прочитанную/обработанную» (находящуюся слева от маркера) и еще не обработанную, находящуюся справа от маркера. Ясно, что если правая часть правила содержит ровно k символов (k = 0, 1, 2, …), то из этого правила может быть образовано в точности k+1 различных конфигураций. Например, из правила S : S + T можно образовать следующие конфигурации (в качестве маркера используется символ ▼): S : ▼ S + T S : S ▼ + T S : S + ▼ T S : S + T ▼ Для любой контекстно-свободной грамматики с конечным количеством правил множество всех возможных различных конфигураций также конечно. Между конфигурациями, состояниями восходящего автомата и операциями, которые должны выполняться в этих состояниях, существуют определенные связи (соотношения), на основании которых может быть определен метод преобразования грамматики в управляющую таблицу. Связи между конфигурациями и операциями. Если в некоторой конфигурации маркер находится перед терминалом (N : ▼t ), то в состоянии номер m, которому соответствует эта конфигурация, должна выполняться операция Shift, осуществляющая переключение автомата в такое состояние, которому соответствует конфигурация с маркером, размещенным после этого терминала (N : t▼ ),. Знак этой операции должен находиться в той клетке управляющей таблицы, которая расположена на пересечении строки состояния m со столбцом, помеченным терминальным символом t (или номером, приписанным этому терминалу). Если маркер в конфигурации N : ▼M находится перед нетерминалом, то в соответствующем ей состоянии m должна выполняться операция Go, осуществляющая переключение автомата в такое состояние, которому соответствует конфигурация с маркером, размещенным после этого нетерминала, т. е. N : M▼ . Знак этой операции должен находиться в той клетке управляющей таблицы, которая расположена на пересечении строки состояния m со столбцом, помеченным нетерминальным символом M (или его номером). И, наконец, если маркер в конфигурации находится после последнего символа правила, то в соответствующем этой конфигурации состоянии должна выполняться операция свертки Rk,n, удаляющая из стека k номеров состояний (ровно столько символов в правой части соответствующего правила), переключающая автомат в состояние, номер которого оказался на верхушке стека после этого удаления, и готовящая номер столбца n управляющей таблицы для последующей операции Go. Связи между конфигурациями и состояниями автомата. Допустим, что каким-либо образом некоторому состоянию поставлена в соответствие определенная конфигурация. Если эта конфигурация имеет вид N : ▼ M , где M – нетерминальный символ, и в грамматике есть правила: M : γ1 M : γ2 ... M : γn , то все конфигурации вида M : ▼ γ1 , M : ▼ γ2 , ... M : ▼ γn также должны быть поставлены в соответствие этому состоянию автомата. Действительно, если в некоторой цепочке терминалов, выводимой из начального нетерминала грамматики, обнаружена подцепочка, выводимая изN, и начинающаяся с цепочки, выводимой из , то автомат в этот момент находится в состоянии, отмеченном маркером в конфигурации N : ▼ M . Поскольку входная цепочка правильна, ее продолжение (а автомат в этот момент находится перед первым символом этого продолжения) обязано выводиться из цепочки M . Следовательно, оно выводится из одной из цепочек вида γi . В силу того, что автомат должен восстановить этот пока еще неизвестный вывод, данному его состоянию должны быть сопоставлены все конфигурации, образуемые путем помещения маркера перед первыми символами порождающих правил для нетерминала M. Это позволит по символам, перед которыми находятся маркеры во вновь образованных конфигурациях, определить для данного состояния знаки операций в управляющей таблице, необходимые для восстановления нужного вывода. Конфигурации вида M : ▼ γi называются дочерними по отношению к исходной (родительской) конфигурации вида N : ▼ M . Если в какой-либо из вновь образованных конфигураций вида M : ▼ γi маркер находится перед нетерминалом L (цепочка γi начинается с этого нетерминала), то данному состоянию автомата должны быть поставлены в соответствие и все конфигурации вида L : ▼ λj (дочерние по отношению к M : ▼ γi). Таким образом, состоянию автомата может соответствовать не одна конфигурация, а некоторое подмножество полного множества конфигураций заданной грамматики. Пусть дано подмножество (одна или несколько конфигураций), сопоставленных состоянию автомата. Применение вышеописанного способа добавления к подмножеству конфигураций, дочерних по отношению к одной или нескольким родительским вплоть до момента, когда это подмножество перестанет изменяться (расширяться), называется его замыканием. При выполнении замыкания новые дочерние конфигурации добавляются к подмножеству только в том случае, если их в нем еще нет. Пусть известно замыкание подмножества конфигураций, соответствующих некоторому состоянию автомата. Разобьем его на более мелкие подмножества, содержащие конфигурации, в которых маркер находится перед одним и тем же символом грамматики. В особое подмножество выделим конфигурации, в которых маркер находится после последнего символа правила. Каждая из конфигураций последнего подмножества (если оно не пусто), имеющая вид X : χ ▼, указывает на необходимость выполнения автоматом, оказавшимся в данном состоянии, операции свертки вида Rk,nx. Здесь k – длина цепочки χ, а nx – номер колонки управляющей таблицы автомата, поставленной в соответствие нетерминальному символу X. Наличие нескольких различных конфигураций в этом подмножестве является причиной возникновения конфликтов типа свертка/свертка. Вернемся к таким конфигурациям данного состояния, в которых маркер находится перед одним и тем же символом w. Очевидно, что если автомат в процессе работы оказался в данном состоянии и его текущим входным символом является w, то должна быть выполнена операция Shift, если w – терминал, или Go, если w – нетерминал. Выполнение такой операции переключает автомат в некоторое другое состояние С, номер которого заносится на верхушку стека. Применительно к подмножеству конфигураций, в которых маркер находится перед символом w, такую операцию следует трактовать как перенос маркера через этот символ. Тем самым образуется подмножество конфигураций, которое должно быть сопоставлено с тем состоянием С, в которое переключается автомат. Состав этого подмножества может впоследствии измениться при его замыкании. Назовем подмножество конфигураций в его начальном составе (в момент образования путем переноса маркера через w) базовым или просто базой по отношению к состоянию С. Таким образом, если известно подмножество конфигураций какого-либо состояния автомата, то могут быть определены базовые подмножества конфигураций, а после выполнения их замыкания – и полные множества конфигураций некоторых других состояний, а именно тех, в которые автомат может переключиться из исходного. В силу того что база начального состояния автомата всегда известна – ею является конфигурация Z : ▼ S ►, на основе рассмотренных связей между состояниями, операциями и конфигурациями может быть построена процедура преобразования грамматики в управляющую таблицу восходящего синтаксического акцептора. Эта процедура выполняется в два этапа. Этап 1. Формирование подмножеств конфигураций, соответствующих состояниям автомата. Определение набора состояний. Этап 2. Преобразование таблицы конфигураций в управляющую таблицу восходящего акцептора. Этап 1. Определение набора состояний восходящего акцептора Подмножества конфигураций, соответствующих состояниям автомата, будем формировать в табличном представлении. Начальное состояние таблицы подмножеств конфигураций (далее – просто таблицы конфигураций) для любой грамматики (с точностью до наименования начального нетерминала грамматики) определяется добавочным правилом и выглядит, как показано в табл. 5.2. Таблица 5.2.
Назначение колонок таблицы конфигураций. Состояние – содержит номер, присвоенный состоянию автомата, определяемому подмножеством конфигураций. Образовано – показывает, из подмножества конфигураций какого состояния образовано данное состояние путем переноса маркера через какой символ (эти сведения понадобятся при формировании знаков операций). База – просто отметка Да, если конфигурация, записанная в строке, является базовой для данного состояния. Конфигурация – пояснения не требуется. Символ – вспомогательная колонка, содержащая тот символ грамматики, перед которым в данной конфигурации находится маркер. Отм. – также вспомогательная колонка. Ее назначение станет ясно из описания процедуры. Начальное состояние таблицы соответствует моменту, когда образована база начального нового состояния. Шаг 1. Замыкание. Просматриваются все конфигурации нового состояния автомата, и если в какой-либо из них маркер находится перед нетерминалом, то каждое правило грамматики, имеющее этот нетерминал в левой части, преобразуется в конфигурацию путем помещения маркера перед первым символом правой части. Для каждой вновь образованной конфигурации просматриваются все строки таблицы данного состояния. Если вновь образованной конфигурации нет ни в одной такой строке, то формируется новая строка. Новая конфигурация заносится в соответствующую клетку этой строки, а в клетку колонки, обозначенной Символ, заносится первый символ правой части правила (если правило имеет вид N : ε, то эта клетка остается пустой), все остальные клетки новой строки оставляются пустыми. Этот шаг выполняется для данного состояния до тех пор, пока не перестанут добавляться новые строки. Построенный фрагмент таблицы конфигураций после выполнения этого шага для нулевого состояния выглядит так, как показано в табл. 5.3. Таблица 5.3.
Шаг 2. Образование новой базы. Просматривается колонка Отм. с целью найти такую строку таблицы, которая еще не помечена и в колонке Символ содержит какой-либо символ грамматики, отличный от псевдотерминала ► (конец файла). Если таких строк нет, то этап построения таблицы конфигураций завершается. Если такая строка найдена, то зафиксируем номер состояния (далее оно называется исходным), найдем и отметим те строки таблицы, которые принадлежат данному состоянию и содержат тот же самый символ в соответствующей колонке. Выберем конфигурации из соответствующей колонки этих строк и перенесем в каждой из них маркер через один символ. Тем самым будет образовано новое базовое подмножество конфигураций. Шаг 3. Проверка наличия состояния с таким набором базовых конфигураций, который совпадает с вновь образованной базой. Просматривается таблица конфигураций и база каждого уже существующего состояния (в том числе исходного) сравнивается с новой базой, сформированной на предыдущем шаге. Возможны два случая. Шаг 3.1. Состояние, имеющее в точности такую же базу, уже существует (подчеркнем, что для этого новая и уже существующая база должны совпадать полностью). В этом случае добавим в колонки Из и Через этого состояния номер исходного состояния и символ, через который был перенесен маркер для образования базы. Эти данные пригодятся на втором этапе при преобразовании таблицы конфигураций в управляющую таблицу. Возвращаемся к шагу 2. Шаг 3.2. Не найдено состояния, имеющего в точности такую же базу, что и проверяемая (вновь образованная). В этом случае создается новое состояние. В таблицу добавляется столько строк, сколько конфигураций содержится в проверяемой базе. Клетки во вновь добавленных строках заполняются в соответствии с назначением колонок. После завершения формирования нового состояния осуществляется возврат к шагу 1. Описание процедуры завершено. Результат ее применения к грамматике Ga1 приведен в табл. 5.4. Заметим, что в колонке Отм. указан порядковый номер применения второго шага процедуры. Шаги с первого по девятый приводили к образованию таких подмножеств базовых конфигураций, которых к моменту выполнения каждого шага еще не было в таблице. Поэтому были сформированы состояния с номерами 1–9. На десятом применении второго шага в результате переноса маркера через символ T были получены конфигурации S: T▼ и T: T▼ * V , в точности совпадающие с базой состояния номер 2. Согласно третьему шагу процедуры новое состояние не создано, в колонке Из состояния 2 отмечено, что его база получена из конфигураций как состояния 0, так и состояния 4. Начиная с одиннадцатого новые состояния были созданы только на 15, 20 и 24 применении второго шага процедуры. Все остальные шаги приводили к образованию уже существующих базовых подмножеств конфигураций. Таблица 5.4.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
