Отчеты оформляются в виде файлов формата Microsoft Word (файлы других форматов не принимаются), размер шрифта 1214

• Название: Отчеты оформляются в виде файлов формата Microsoft Word (файлы других форматов не принимаются), размер шрифта 1214
• Дата: 06.04.2023
• Размер: 452.53 Kb.
• Имя файла: LabJob23.docx
• Тип: Отчет; #1041909
• страница: 3 из 12

Лабораторная/практическая работа № 3

1. 
   Название работы: «Синтаксис языков программирования. Формальные грамматики».
   
2. 
   Цели работы: изучение основных понятий метаязыка формальных грамматик, свойств грамматик и нетерминальных символов, рекурсивности и однозначности грамматик, недостижимости, бесплодности, аннулируемости и рекурсивности нетерминальных символов, отношений предшествования и последования между символами, приобретение навыков разработки формальных грамматик.
   
3. 
   Основные теоретические сведения:
   

1. 
   Формальные грамматики
   

Формальной грамматикой G называется совокупность

G = { A_t, A_n, S , P},

состоящая:

• 
  из алфавита терминальных символов A_t;
  
• 
  алфавита нетерминальных символов A_n;
  
• 
  начального нетерминального символа S;
  
• 
  системы правил подстановки P
  

Алфавит терминальных символов A_t есть конечное множество всех слов языка, порождаемого данной грамматикой. Понятие «терминальный» в данном случае обозначает неразложимость, элементарность таких символов с точки зрения синтаксических правил.

Например, любой идентификатор при синтаксическом анализе считается простейшим символом, даже если он является цепочкой из нескольких литер. Более того, под одиночным терминальным символом, как правило, понимается вся группа слов, таких как идентификаторы или константы. В самом деле, с точки зрения синтаксиса, как совокупности правил образования предложений из слов, совершенно безразлично, какой именно идентификатор находится в левой части оператора присваивания или какие именно константы содержатся в выражении.

Наряду со словосочетанием «терминальный символ» будет использоваться просто слово «терминал».

В дальнейшем терминальные символы обозначаются либо одиночными литерами, представляющими собой отдельные слова в языках программирования (+, *, =, ;, {, }, …), либо терминами, называющими слово или группу слов (идентификатор, константа, id, const, …), либо просто малыми буквами латинского алфавита, обозначающими произвольный терминал (a, b, c, …).

Например: A_t={идентификатор, константа, +, –, *, /, =}

Алфавит нетерминальных символов A_n есть конечное множество названий синтаксических конструкций, например: <предложение>, <выражение>, <список аргументов>, <условный оператор>, <тело функции>. Нетерминальные символы используются только в метаязыке, на котором описывается язык программирования, никакой нетерминальный символ не может появиться в тексте правильной программы. Наряду со словосочетанием «нетерминальный символ» в дальнейшем будет использоваться просто «нетерминал». Нетерминальные символы принято обозначать либо словосочетаниями в угловых скобках, как в начале этого абзаца, либо словами, начинающимися с прописной буквы и содержащими буквы, цифры и символы подчеркивания (например – Function, ArgList, Const_16), либо просто большими буквами латинского алфавита в курсивном начертании A, B, C, ... Z.

Начальный нетерминальный символ S есть один из нетерминальных символов. Этим символом обычно обозначается наиболее общая синтаксическая конструкция, например: <правильная программа>.

Символы (как терминальные, так и нетерминальные) могут образовывать цепочки, которые будут обозначаться малыми буквами греческого алфавита α, β, γ, ... ω. Особое значение будет играть пустая цепочка символов ε.

Система правил подстановки P (иногда называемая системой порождающих правил или продукций) есть конечное множество пар цепочек вида α : β, причем цепочка α (левая часть правила) должна содержать хотя бы один нетерминальный символ.

Каждая такая пара цепочек называется правилом подстановки (порождающим правилом, продукцией) и определяет возможный способ замены левой части правила на его правую часть. Правила подстановки обычно нумеруются, причем в левой части правила с номером 1 должен находиться одиночный начальный нетерминал грамматики.

Для иллюстрации приведем пример фрагмента грамматики С-подобного языка (пока будем считать этот фрагмент полноценной грамматикой G₁):

S : S + T

S : S – T

S : T

T : ident

T : const

Лексические правила для терминалов ident и const пока не будем считать частью этой грамматики. Эта грамматика порождает (определяет как правильные) предложения арифметические выражения, содержащие только идентификаторы, константы и знаки операций сложения и вычитания.

2. 
   Дерево грамматического разбора
   

Пусть дана грамматика G с системой порождающих правил P.

Цепочка ψ непосредственно выводится из цепочки σ (σ  ψ), если:

• 
  σ = ω α δ, где ω и δ – произвольные, возможно пустые цепочки;
  
• 
  ψ = ω β δ, где ω и δ – те же самые цепочки;
  
• 
  в системе порождающих правил P есть правило α : β.
  

Подстановка цепочки β вместо α в цепочке σ = ω α δ порождает ω β δ, т. е. цепочку ψ. Обратная подстановка не подразумевается, т.е. из возможности непосредственного вывода σ  ψ не следует возможность непосредственного вывода ψ  σ.

Например, в грамматике G₁ цепочка S + const непосредственно выводится из цепочки S + T путем подстановки правой части правила T : const вместо T.

Цепочка ψ выводится из цепочки σ обозначается (σ  ψ), если существует последовательность непосредственных выводов:

σ  ψ₁  ψ₂  ψ₃ ... ψ_n  ψ

Например, в грамматике G₁ цепочка x – 1 выводится из начального гнетерминала S путем выполнения такой последовательности непосредственных выводов: SS – TT – Tident – Tx – Tx – constx - 1.

Правильным предложением языка L, определяемого грамматикой G, называется цепочка, состоящая только из терминальных символов и выводимая из начального нетерминала S. Любая цепочка терминальных символов, для которой не существует вывода из начального нетерминала S грамматики G, является неправильным предложением языка L. Цепочка, содержащая символы, не входящие в алфавит терминальных символов A_t, в частности, нетерминальные символы, вообще не является предложением языка L.

Таким образом, грамматика G разбивает бесконечное множество всех возможных цепочек, содержащих только терминальные символы (слова языка), на два непересекающихся подмножества:

• 
  подмножество правильных предложений, которое собственно и является языком L, порождаемым грамматикой G;
  
• 
  подмножество неправильных предложений.
  

Вывод правильного предложения можно представить в графической форме, сопоставив символам цепочек узлы, а применению правил - дуги графа. Такая форма обычно называется деревом грамматического разбора.

Основная задача синтаксического акцепта – проверка правильности последовательности слов транслируемой программы – формулируется так: предложение языка (т. е. последовательность терминалов порождающей язык грамматики) является правильным, если может быть установлен факт существования дерева его грамматического разбора, и неправильным в противном случае.

Само дерево разбора при этом можно и не строить, достаточно только выяснить, возможно ли это. Сложность задачи восстановления дерева разбора предложений языка (или выяснения факта его существования) существенно зависит от свойств грамматики, определяющей этот язык.

Любая грамматика G определяет единственный язык L. Однако существуют языки, для определения которых можно построить более чем одну грамматику (различающимися считаются грамматики, для которых деревья грамматического разбора хотя бы одного правильного предложения данного языка имеют разную структуру). Таков, например, язык скобочных арифметических выражений со знаками операций различного приоритета, две разные грамматики которого показаны в табл. 3.1.

Таблица 3.1

Грамматика Ga1			Грамматика G a2
1	S : S + T		1	S : U R
2	S : T		2	R : + S
3	T : T * V		3	R :
4	T : V		4	U : V W
5	V : ( S )		5	W : * U
6		V : ident	6	W :
7		V : const	7	V : ( S )
			8	V : ident
			9	V : const

Эти две грамматики различаются не только количеством правил и обозначениями нетерминалов. Пусть дано предложение ( a + b ) * с, где a, b и с – идентификаторы (или константы). Построим выводы этого предложения из начальных нетерминалов грамматик G_a1 и G_a2, заменяя на каждом шаге самый левый нетерминал в очередной цепочке символов на правую часть одного из правил для этого нетерминала:

Для G_a1:

S  T  T*V  V*V  (S)*V  (S+T)*V  (T+T)*V (V+T)*V 
(a+T)*V  (a+V)*V  (a+b)*V  (a+b)*c

Для G_a2:

S  UR  VWR  (S)WR  (UR)WR (VWR)WR (aWR)WR  (aR)WR  (a+S)WR  (a+UR)WR  (a+VWR)WR  (a+bWR)WR  (a+bR)WR  (a+b)WR  (a+b)*UR (a+b)*VWR  (a+b)*cWR  (a+b)*cR  (a+b)*c

Даже не преобразуя эти два вывода в графически представленные деревья грамматического разбора, легко можно заметить, что эти деревья существенно отличаются друг от друга. Таким образом, действительно существуют эквивалентные, но различающиеся по своим свойствам грамматики, определяющие один и тот же язык.

Свойства грамматик оказывают большое влияние как на принципиальную возможность использования данной грамматики для синтаксического анализа, так и на применимость средств автоматизации построения синтаксических анализаторов.

Все грамматики можно разделить на четыре основных класса по Хомскому, впервые сформулировавшему приведенные ниже признаки деления на иерархически вложенную систему классов: общие, контекстно-зависимые, контекстно-свободные и регулярные.

Для целей построения синтаксических анализаторов трансляторов наилучшим образом подходят контекстно-свободные грамматики, у которых левая часть каждого правила представляет собой в точности один нетерминал, а на правые части не накладывается никаких ограничений. Они позволяют определять синтаксис формальных языков, в том числе языков программирования, т.е. совокупность правил построения предложений языка из его слов.

Независимость от контекста означает возможность подстановки правой части любого из правил для замены нетерминала из левой части правила в любой цепочке, содержащей этот нетерминал.

3. 
   Свойства контекстно-свободных грамматик
   

Свойства любой грамматики полностью определяются ее системой порождающих правил и могут служить основанием для разбиения всего класса контекстно-свободных грамматик на более узкие подклассы. Для некоторых подклассов контекстно-свободных грамматик известны эффективные алгоритмы автоматизации проектирования трансляторов для порождаемых или языков.

Наиболее важными свойствами грамматик в целом являются рекурсивность и однозначность.

Рекурсивность

Нетерминальный символ X называется рекурсивным, если из него могут быть выведены цепочки, содержащие сам этот символ X, т. е.

X  μ X η,

Существует много вариантов свойства рекурсивности нетерминалов: прямая и косвенная, левая, правая и общая. Эти варианты могут сочетаться произвольным образом. Грамматика называется рекурсивной, если рекурсивен хотя бы один нетерминальный символ, и нерекурсивной в противном случае.

Нерекурсивные грамматики с конечным количеством порождающих правил определяют так называемые конечные языки, в которых количество правильных предложений ограничено. Такие языки и грамматики не представляют практического интереса.

Однозначность

Грамматика называется однозначной, если любое правильное предложение порождаемого ею языка имеет единственное дерево грамматического разбора, и неоднозначной в противном случае. Грамматики G_a1и G_a2 являются однозначными, но для того же самого языка можно привести пример неоднозначной грамматики, показанный в табл. 3.2.

Выявление свойства однозначности некоторой грамматики является алгоритмически неразрешимой проблемой. Не существует универсального алгоритма, способного для любой заданной контекстно-свободной грамматики определить, однозначна ли она. Известно, что методы построения синтаксических анализаторов путем преобразования формальной грамматики в конечный автомат не приводят к желаемому результату для неоднозначных грамматик. Другими словами, неоднозначные грамматики непригодны для преобразования в конечный автомат (со стековой памятью), выполняющий функции синтаксического анализатора. Однако и многие однозначные грамматики также не допускают подобного преобразования, но по другим причинам.

Таблица 3.2

Грамматика Ga3
1	S : S + S
2	S : T
3	T : T * T
4	T : V
5	V : ( S )
6	V : ident
7	V : const

Кроме общих свойств грамматик важное значение для решения задач синтаксического анализа имеют некоторые свойства нетерминальных символов и отношения между символами грамматики.

Свойства символов грамматики

Аннулируемость

Нетерминальный символ называется аннулируемым, если из него может быть выведена пустая цепочка символов. В противном случае нетерминал называется неаннулируемым. В литературе по формальным языкам такие символы обычно называются аннулирующими и неаннулирующими.

Это свойство нетерминальных символов может иметь важное значение для свойств грамматики в целом и ее применимости в том или ином методе синтаксического анализа.

Недостижимость

Символ (терминальный или нетерминальный) называется недостижимым, если он не появляется ни в одной цепочке символов, выводимой из начального нетерминала грамматики.

Бесплодность

Нетерминальный символ называется бесплодным, если из него не может быть выведена цепочка, состоящая только из терминалов.

Недостижимые и бесплодные нетерминалы могут появиться в грамматике либо в результате ошибок при разработке ее системы порождающих правил, либо в результате эквивалентных преобразований грамматики с целью изменения ее свойств или свойств ее символов. Все правила, содержащие такие символы, следует удалить из грамматики (а сами символы из ее алфавитов). Алгоритмы вычисления свойств символов грамматики следует изучить по [1].

Кроме свойств отдельных символов большое значение для целей синтаксического анализа имеют некоторые отношения между символами, определяемые всей совокупностью правил грамматики.

Важнейшими отношениями являются отношение предшествования и отношение следования. Эти отношения вычисляются в виде множеств, сопоставляемых с символами грамматики и содержащих опять-таки символы этой грамматики.

4. 
   Множества предшественников символов грамматики
   

Предшественником некоторого символа X называется символ, с которого начинается цепочка, выводимая из X. Считается, что любой символ является предшественником самого себя (т. е. допускается вывод длины 0).

Термин «предшественник» в русском языке имеет несколько другой смысл: нечто, появляющееся до того, чему оно предшествует. Тем не менее в литературе по формальным языкам и грамматикам (и в настоящем учебнике) этот термин используется именно в том смысле, который определен в предыдущем абзаце.

5. 
   Множества предшественников цепочек символов
   

При построении синтаксических анализаторов часто приходится оперировать не с отдельными символами, а с цепочками символов.

В множество предшественников цепочки  входят те и только те терминальные символы, с которых начинаются цепочки, выводимые из .

Если известны множества предшественников одиночных символов грамматики, то можно легко сформулировать способ определения множеств предшественников произвольных цепочек символов.

Пусть цепочка имеет вид  = ABCD..., где A, B, C, D, ... – произвольные (не обязательно нетерминальные) символы грамматики. Пусть также известны множества предшественников всех символов грамматики.

Тогда множество предшественников цепочки  можно вычислить по следующей формуле: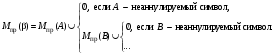



Здесь 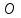– пустое множество, под неаннулируемым символом понимается либо терминал, либо неаннулируемый нетерминал.

6. 
   Множества последователей символов грамматики
   

Символ Y называется последователем символа X, если хотя бы в одной цепочке ω, выводимой из начального нетерминала грамматики, символ Y непосредственно следует за X:

S  ω = ... X Y ...

Это определение понятия последования не является конструктивным. Для того чтобы можно было понять, что такое последователи и построить процедуру определения множеств последователей для символов грамматики, нужно точно сформулировать условия возникновения отношения последования.

Символ Y является непосредственнымпоследователем символа X, если выполняется либо условие 1, либо условие 2:

Условие 1. В грамматике есть правило вида

N :  XY , где  и  – произвольные, возможно пустые цепочки.

Условие 2. В грамматике есть правило вида

N :  X  Y , где  и  – произвольные, возможно пустые цепочки, а  – цепочка, состоящая только из аннулируемых нетерминалов.

Непосредственными последователями, к сожалению, полные множества последователей символов грамматики не исчерпываются.

Символ Y является последователем символа X, если Y является последователем (неважно – непосредственным или нет) некоторого символа Z и выполняется условие 3:

Условие 3. В грамматике есть правило вида

Z : χ X , где χ – произвольная, возможно пустая цепочка, а  – цепочка, либо состоящая только из аннулируемых нетерминалов, либо просто пустая.

И, наконец, символ Y является последователем символа X, если Y есть последователь некоторого символа Z (неважно, непосредственный или нет)и выполняется условие 4:

Условие 4. В грамматике есть совокупность правил следующего вида:

Z	:	χ1Z11
Z 1	:	χ2Z22
...
Zn-1	:	χn Znn
Zn	:	χ0X0,

где χ₀, χ₁,..., χ_n – произвольные цепочки, а ₀, ₁,..., _n – цепочки, состоящие только из аннулируемых нетерминалов или просто пустые.

Условия 1 и 2 определяют отношение «символ Y есть непосредственный последователь символа X», а условия 3 и 4 – отношение «символ X есть последний (замыкающий) символ в цепочке, выводимой из символа Z». Искомое отношение «символ Y есть последователь символа X» является произведением этих двух отношений.

Хотя для решения задачи синтаксического анализа интерес представляют только множества последователей нетерминальных символов, для их вычисления приходится определять множества последователей всех (терминальных и нетерминальных) символов грамматики.

Множества предшественников и последователей символов грамматики будут самым существенным образом использоваться в процессе преобразования формальных грамматик в синтаксические акцепторы, т.е. при выполнении всех лабораторных работ 3-8 и курсовой работы.

4. 
   Порядок выполнения работы (рекомендуется использовать в качестве примера систему правил Samples/Sample3):
   

1. 
   Разработать описание синтаксиса языка, заданного на курсовую работу. Описание синтаксиса должно включать:
   

• 
  структуру файла программы (состав модулей/секций файла);
  
• 
  структуру и назначение каждой секции/модуля;
  
• 
  формат и точный способ выполнения всех операторов (присваивания, цикла, …) в виде последовательности операций, сложность которых не выше сложения/ умножения/сравнения/… двух значений, условного или безусловного перехода.
  

1. 
   Используя систему правил Samples/Sample3 как основу:
   

• 
  освоить и изучить ввод и редактирование синтаксических правил, содержащих слова-строки, группирование, операции выбора и квантификаторы;
  
• 
  проанализировать соответствие фактических правил видимым/редактируемым правилам в процессе редактирования системы правил; понять, как выявляется начальный нетерминал грамматики;
  
• 
  разобраться в причинах возникновения недоступных и бесплодных нетерминалов, отображаемых серым цветом и отсутствующих в системе фактических правил после завершения ввода правил, содержащих такие символы;
  
• 
  разобраться в том, каким образом пакет ВебТрансБилдер разделяет правила на лексические и синтаксические; описать принципы этого разделения.
  

1. 
   Изучить по [2-5] теоретические определения и алгоритмы вычисления отношений предшествования и последования для символов грамматики.
   
2. 
   Освоить просмотр свойств грамматик и их символов в пакете ВебТрансБилдер; необходимо достичь понимания того, почему те или иные символы грамматики имеют свой конкретный набор свойств (пункты меню «Показать/Правила грамматики», «Показать/Множества предшественников» и «Показать/Множества последователей»).
   
3. 
   Используя полученные навыки работы с грамматиками и программным обеспечением, начать поэтапную разработку грамматики языка для заданного варианта курсовой работы, реализовать правила, определяющие как минимум выражения со всеми знаками операций языка, заданного на курсовую работу, оператор присваивания и не менее одного управляющего оператора.
   
4. 
   Выполнить построение транслятора по разработанной грамматике и шаблону табличного восходящего анализатора для языка JavaScript. Проверить работоспособность построенного транслятора на фрагментах тестовых программ, написанных на заданном языке; добиться того, чтобы выражения и выполняемые операторы воспринимались транслятором как правильные.
   
5. 
   Подготовить, сдать и защитить отчет к лабораторной работе.
   

5. 
   Требования к содержанию отчета.
   

Отчет должен содержать:

• 
  цель работы;
  
• 
  описание синтаксиса языка как результат выполнения пункта 4.1 и как часть расчетно-пояснительной записки к курсовой работе;
  
• 
  результаты разработки (пункт 4.5) и тестирования (пункт 4.6) грамматики для языка, заданного на курсовую работу;
  
• 
  матричное представление отношений предшествования и последования для символов этой грамматики, сформированное пакетом ВебТрансБилдер; краткое описание этих отношений;
  
• 
  результаты своего анализа алгоритмов и способов преобразования видимой системы правил в фактическую, выявления или формирования начального нетерминала, разделения правил на лексические и синтаксические, выявления недостижимых и бесплодных нетерминалов; этот анализ должен быть проведен для результата выполнения пункта 4.5;
  
• 
  выводы и заключение.
  

6. 
   Контрольные вопросы.
   

1. 
   Что такое терминальные и нетерминальные символы формальных грамматик?
   
2. 
   Что такое рекурсия? Перечислите виды рекурсии.
   
3. 
   Что такое контекстно-свободные грамматики?
   
4. 
   Вычислите множество предшественников цепочки символов
   WR для грамматики G_a2.
   
5. 
   Является ли однозначной грамматика:
   

1. 
   S : S "|" S
   
2. 
   S : S S
   
3. 
   S : "(" S ")"
   
4. 
   S : ident
   

1. 
   Что такое аннулируемый нетерминал?
   
2. 
   Что такое стековая память? Какие операции обычно определяются над стековой памятью?
   
3. 
   Что такое множество последователей символа грамматики?
   
4. 
   Чем понятие вывода отличается от понятия непосредственного вывода?
   
5. 
   Что такое недетерминированность конечного автомата без памяти? Какие бывают виды недетерминированности?
   
6. 
   Устраните левую рекурсию в такой грамматике:
   

1. 
   S : "(" L ")"
   
2. 
   S : ident
   
3. 
   L : L "," S
   
4. 
   L : S
   

1. 
   Что такое дерево грамматического разбора?
   
2. 
   Какие нетерминальные символы называются бесплодными?
   
3. 
   Что такое рекурсивный цикл в грамматике?
   
4. 
   Какие грамматики называются эквивалентными?
   
5. 
   Могут ли быть эквивалентными два конечных автомата без памяти, имеющие разное количество финальных состояний?
   
6. 
   Вычислите множества последователей для грамматики из вопроса 6.5.
   
7. 
   Что такое контекстно-зависимая грамматика?
   
8. 
   Что такое отношение предшествования символов?
   
9. 
   Можно ли удалить из грамматики пряморекурсивный нетерминал?
   
10. 
    Постройте дерево разбора предложения (ident, (ident, ident)) в грамматике из вопроса 6.11.
    
11. 
    Что такое факторизация?
    
12. 
    Сформулируйте физический смысл перехода по пустой цепочке в финальное состояние конечного автомата без памяти.
    
13. 
    Можно ли и, если можно, то как преобразовать косвенную рекурсию в прямую?
    
14. 
    Определите алфавиты терминальных и нетерминальных символов для грамматики из вопроса 6.11.
    
15. 
    Какие конечные автоматы без памяти называются эквивалентными?
    
16. 
    Перечислите условия, которые определяют отношение последования символов грамматики.
    
17. 
    Вычислите вручную множества предшественников и последователей и все свойства символов для фрагмента грамматики, определяющий синтаксис условного оператора языка С:
    

1. 
   Operator : …
   
2. 
   Operator : "if" "(" LogicalExpression ")" Operator Rest
   
3. 
   Rest : "else" Operator
   
4. 
   Rest :
   

29. 
    Является ли грамматика вопроса 6.29 однозначной?
    
30. 
    Как соотносятся между собой языки и грамматики?
    
31. 
    Могут ли быть эквивалентными два конечных автомата без памяти, имеющие различное количество рабочих состояний?
    
32. 
    Как вычисляется множество предшественников цепочки символов?
    
33. 
    Почему из системы порождающих правил грамматики не может быть удален ее начальный нетерминал?
    
34. 
    Как связаны между собой понятия вывода и дерева грамматического разбора?