Пермский государственный технический университет

• Название: Пермский государственный технический университет
• Дата: 25.02.2023
• Размер: 0.82 Mb.
• Имя файла: DiffUr.doc
• Тип: Документы; #954925
• страница: 1 из 3

Федеральное агентство по образованию

Государственное образовательное учреждение

высшего профессионального образования

ПЕРМСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Дифференциальные уравнения

Индивидуальные задания

Пособие разработано ст. преп. Пепеляевой Н. В. Одобрено методической комиссией кафедры «Высшая математика» © 2007, каф. «Высшая математика» ПГТУ

Пермь 2007

Задания:

1. 
   Найти общий интеграл дифференциального уравнения
   
2. 
   Найти общий интеграл дифференциального уравнения
   
3. 
   Найти решение задачи Коши
   
4. 
   Найти общее решение дифференциального уравнения
   
5. 
   Найти решение задачи Коши
   
6. 
   Найти общий интеграл дифференциального уравнения
   
7. 
   Найти общее решение дифференциального уравнения
   
8. 
   Найти решение задачи Коши
   
9. 
   Найти частное решение дифференциального уравнения
   
10. 
    Найти общее решение дифференциального уравнения
    
11. 
    Решить систему дифференциальных уравнений
    
12. 
    Найти решение задачи Коши
    
13. 
    Задачи по геометрии
    
14. 
    Задачи по физике
    

Вариант 1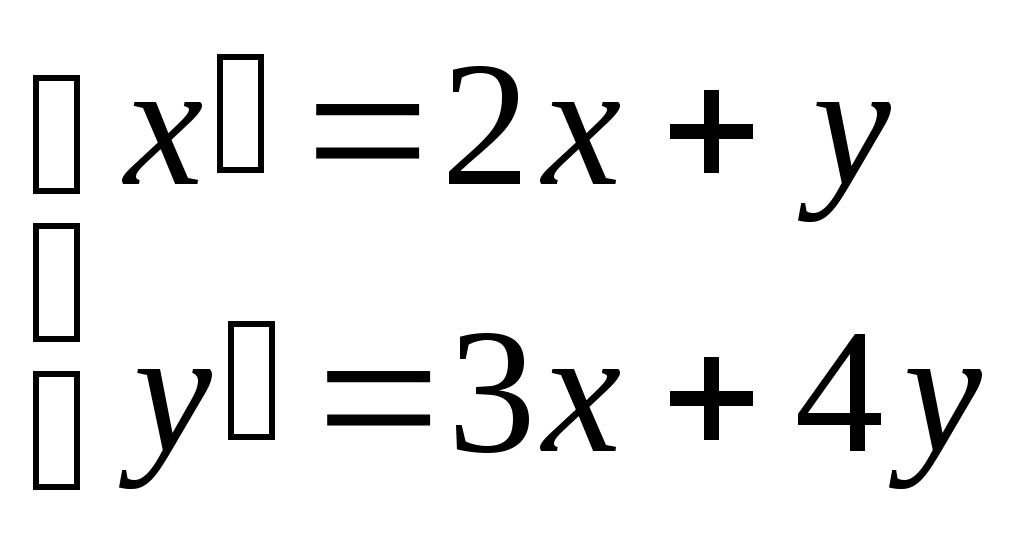

1. 
   
   
2. 
   
   
3. 
   
   
4. 
   
   
5. 
   
   
6. 
   
   
7. 
   
   
8. 
   
   
9. 
   
   
10. 
    
    
11. 
    
    
12. 
    
    
13. 
    Найти кривую, каждая касательная к которой отсекает на осях координат такие отрезки, что сумма величин, обратных квадратам длин этих отрезков равна единице.
    
14. 
    Найти уравнение движения парашютиста массой m, если сила сопротивления воздуха f пропорциональна скорости движения с коэффициентом k.
    

Вариант 2

1. 
   
   
2. 
   
   
3. 
   
   
4. 
   
   
5. 
   
   
6. 
   
   
7. 
   
   
8. 
   
   
9. 
   
   
10. 
    
    
11. 
    
    
12. 
    
    
13. 
    Найти уравнение кривой, проходящей через точку А(0; 5), если известно, что угловой коэффициент касательной в любой точке ее равен ординате этой точки, увеличенной в 7 раз.
    
14. 
    За какое время вытечет вода из цилиндра радиуса R и высотой H, стоящего вертикально, через отверстие радиуса r в дне. Указания: истечение жидкости подчиняется закону Торричелли: .
    

Вариант 3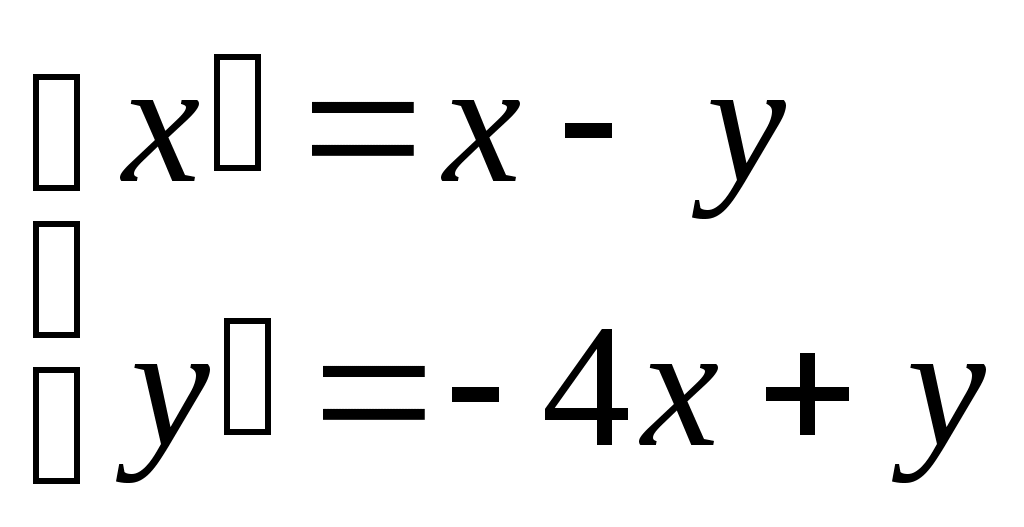

1. 
   
   
2. 
   
   
3. 
   
   
4. 
   
   
5. 
   
   
6. 
   
   
7. 
   
   
8. 
   
   
9. 
   
   
10. 
    
    
11. 
    
    
12. 
    
    
13. 
    Найти линию, зная, что площадь, заключенная между осями координат, этой кривой и ординатой любой точки на ней, равна кубу этой ординаты.
    
14. 
    Согласно закону Гука эластичный шнур длины l под действием силы F получает приращение длины, равное klF(k - константа). Шнур длиной 3 см подвешен за один его конец. На сколько увеличится длина шнура, если его вес равен 2Н.
    

Вариант 4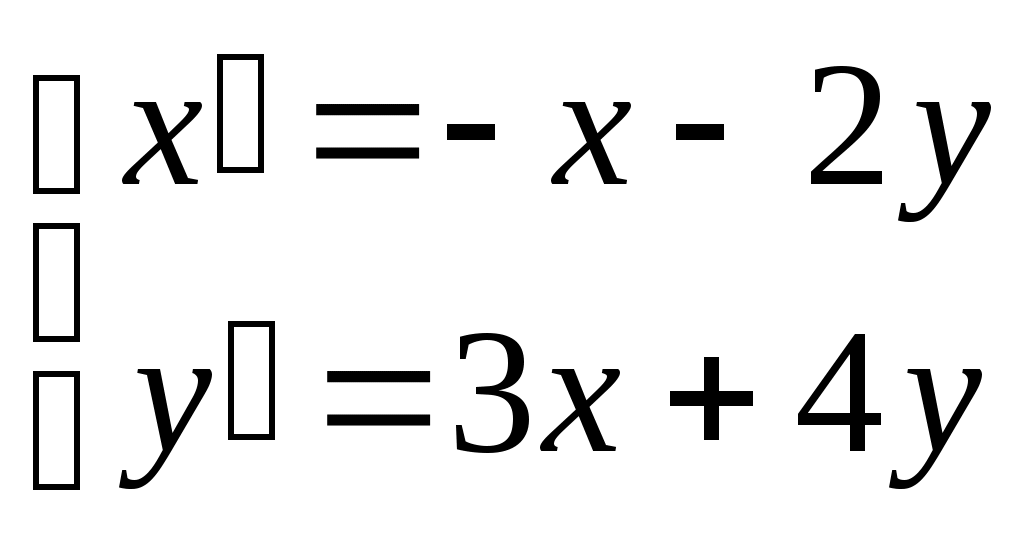

1. 
   
   
2. 
   
   
3. 
   
   
4. 
   
   
5. 
   
   
6. 
   
   
7. 
   
   
8. 
   
   
9. 
   
   
10. 
    
    
11. 
    
    
12. 
    
    
13. 
    Площадь, ограниченная кривой, осями координат и ординатой какой – либо точки кривой, равна длине соответствующей дуги кривой. Найти уравнение этой линии, если известно, что она проходит через точку М(0; 1).
    
14. 
    Определить удлинение свободно подвешенного стержня длиной а см под действием его собственного веса. Указание: удлинение стержня подчиняется закону Гука.
    

Вариант 5

1. 
   
   
2. 
   
   
3. 
   
   
4. 
   
   
5. 
   
   
6. 
   
   
7. 
   
   
8. 
   
   
9. 
   
   
10. 
    
    
11. 
    
    
12. 
    
    
13. 
    Найти уравнение линии, у которой отрезок, отсекаемый касательной в любой точке кривой на оси Оу, равен квадрату абсциссы точки касания.
    
14. 
    Луч от источника света поглощается окружающей средой. Считается, что поглощение света между шарами с радиусами r и r + Δr и с центрами в источнике света, с точностью до малых высшего порядка, равно . Определи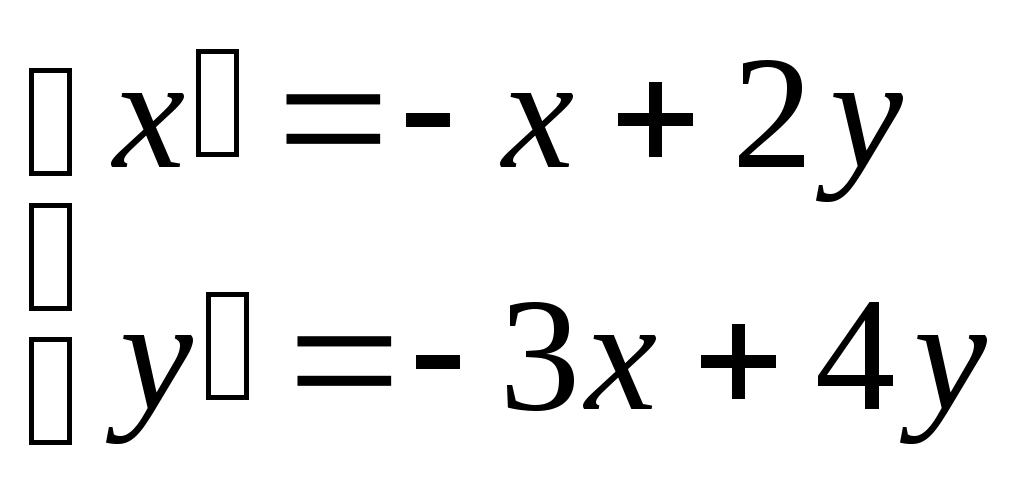ть зависимость яркости f от расстояния r, если k – коэффициент пропорциональности.
    

Вариант 6

1. 
   
   
2. 
   
   
3. 
   
   
4. 
   
   
5. 
   
   
6. 
   
   
7. 
   
   
8. 
   
   
9. 
   
   
10. 
    
    
11. 
    
    
12. 
    
    
13. 
    Найти уравнение линии, зная, что отрезок, отсекаемый касательной от оси ординат равен полусумме координат точки касания.
    
14. 
    На материальную точку с массой m, движущуюся прямолинейно, действует в направлении движения сила с коэффициентом пропорциональности k и сила сопротивления среды, пропорциональная скорости и времени с коэффициентом пропорциональности k₁. найти зависимость скорости от времени, если в начальный момент времени скорость была равна V₀.
    

Вариант 7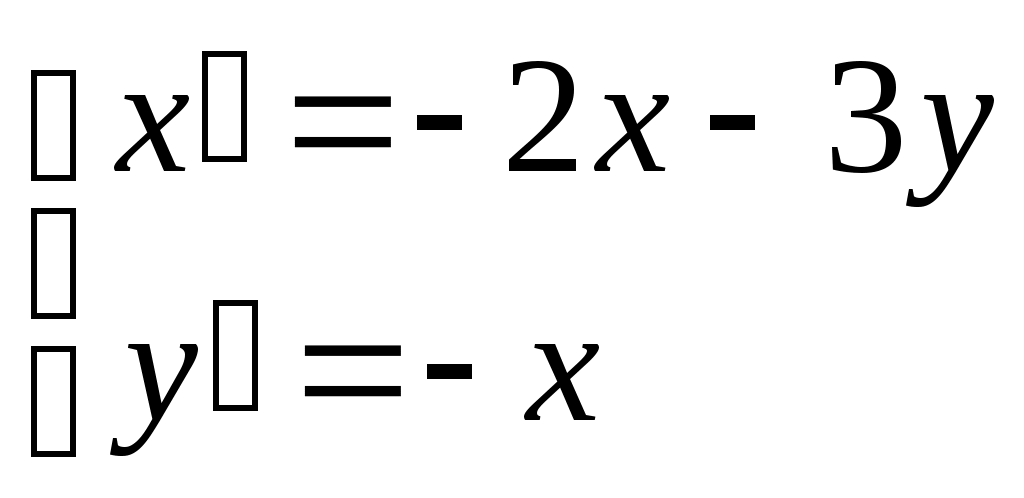

1. 
   
   
2. 
   
   
3. 
   
   
4. 
   
   
5. 
   
   
6. 
   
   
7. 
   
   
8. 
   
   
9. 
   
   
10. 
    
    
11. 
    
    
12. 
    
    
13. 
    Найти уравнение линии, для которой произведение абсциссы какой – либо точки на величину отрезка, отсекаемого нормалью на оси ординат, равно удвоенному квадрату расстояния от этой точки до начала координат.
    
14. 
    За 30 дней распалось 50% первоначального количества радиоактивного вещества. Через сколько времени останется 1% первоначального количества, если известно, что количество радиоактивного вещества, распадающегося за единицу времени, пропорционально наличному количеству этого вещества в данный момент.
    

Вариант 8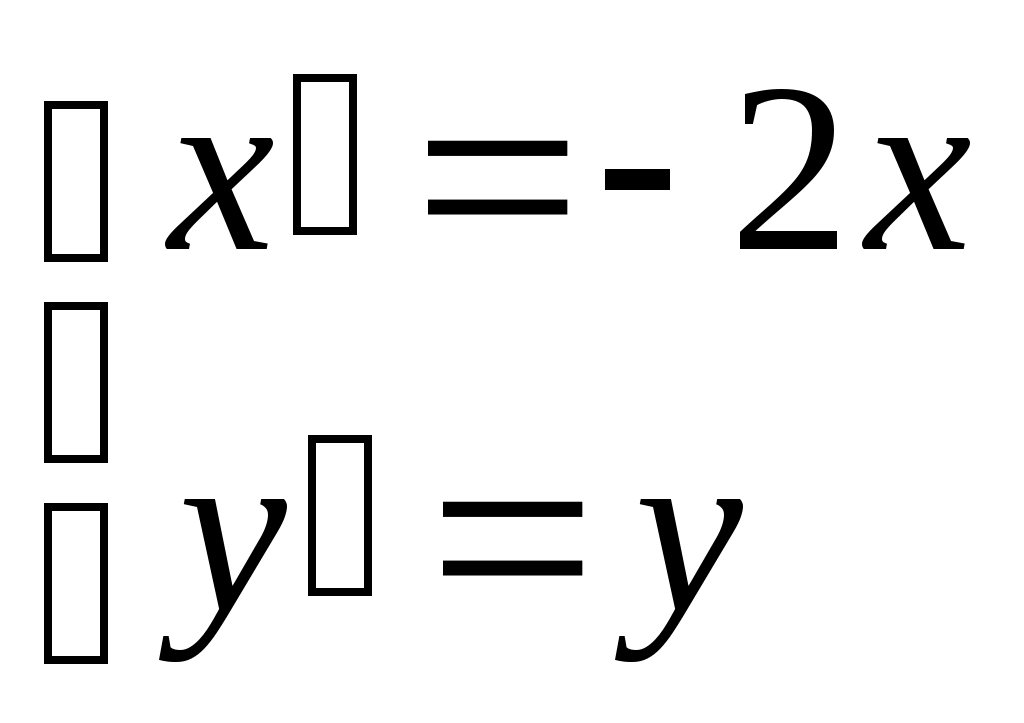

1. 
   
   
2. 
   
   
3. 
   
   
4. 
   
   
5. 
   
   
6. 
   
   
7. 
   
   
8. 
   
   
9. 
   
   
10. 
    
    
11. 
    
    
12. 
    
    
13. 
    Найти линию, для которой треугольник, образованный нормалью с осями координат, был бы равновелик треугольнику, образованному осью OX, касательной и нормалью.
    
14. 
    Тело массой m=2, брошено вертикально вверх со скоростью , испытывает сопротивление воздуха, которое пропорционально скорости движения (K=0.04). Определить с точностью до время Т, которое требуется для того, чтобы тело упало на землю, и максимальную высоту, на которую поднимется тело.
    

Вариант 9

1. 
   
   
2. 
   
   
3. 
   
   
4. 
   
   
5. 
   
   
6. 
   
   
7. 
   
   
8. 
   
   
9. 
   
   
10. 
    
    
11. 
    
    
12. 
    
    
13. 
    Найти линию, проходящую через точку А(2;3) и обладающую тем свойством, что отрезок любой её касательной, заключенный между координатными осями, делится пополам в точке касания.
    
14. 
    Тело нагрето до температуры и затем (в момент времени ) помещено в среду с температурой . Каким должен быть коэффициент теплопроводности тела К ( ), чтобы было минимальным среднее квадратичное отклонение температуры u(t) тела от заданной величины за время Т=1,5ч, т.е. ? Вычисления вести с точностью до 0,01