ЛР1 5 вариант. Первичный эконометрический анализ. Корреляционный анализ
 Скачать 116.35 Kb. Скачать 116.35 Kb.
|
Задание 3. Проверка гипотезы на основе критерия χ2-ПирсонаСформулировать и проверить гипотезу согласии выборочных данных с нормальным распределением на основе критерия χ2-Пирсона. Сделать выводы. К таблицам, которые строили во втором задании, нам нужно добавить столбцы с теоретической частотой (Ei) и статистикой хи-квадрат Пирсона. Выдвинемдве гипотезы для каждого показателя (Х): 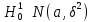 – основная гипотеза – основная гипотеза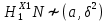 – альтернативная гипотеза – альтернативная гипотезаПри справедливости гипотезы согласия с нормальным распределением статистика Хи2 имеет распределение Хи2 –Пирсона c 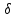 =K-3 степенями свободы. =K-3 степенями свободы.Если 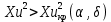 , то гипотеза о нормальном распределении отвергается с доверительной вероятностью , то гипотеза о нормальном распределении отвергается с доверительной вероятностью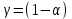 . .Чтобы проверить не отвергается ли гипотеза необходимо рассчитать Хи2 критическое. Для этого воспользуемся формулой в Excel. После расчета получаем значение 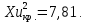 Составим вспомогательные таблицы Дополнение к таблице 3
36,58 больше 7,81. Это означает, что гипотеза согласия 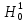 отвергается с вероятностью 0,95. Х1 (посетители) не имеют нормального распределения. отвергается с вероятностью 0,95. Х1 (посетители) не имеют нормального распределения.Дополнение к таблице 4
7,32 меньше 7,81. Это означает, что гипотеза согласия 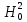 не отвергается. Х2 (томаты) имеют нормальное распределение. не отвергается. Х2 (томаты) имеют нормальное распределение.Дополнение к таблице 5
0,67 меньше 7,81. Это означает, что гипотеза согласия 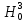 не отвергается. Х3 (лапша) имеет нормальное распределение. не отвергается. Х3 (лапша) имеет нормальное распределение.Дополнение к таблице 6
23,54 больше 7,81. Это означает, что гипотеза согласия 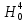 отвергаетсяс вероятностью 0,95. Х4 (мука) не имеет нормального распределение. отвергаетсяс вероятностью 0,95. Х4 (мука) не имеет нормального распределение.Дополнение к таблице 6
9,67 больше 7,81. Это означает, что гипотеза согласия 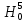 отвергаетсяс вероятностью 0,95. Х5 (крупа) не имеет нормального распределение. отвергаетсяс вероятностью 0,95. Х5 (крупа) не имеет нормального распределение. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
