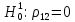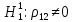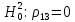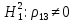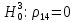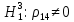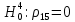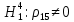ЛР1 5 вариант. Первичный эконометрический анализ. Корреляционный анализ
 Скачать 116.35 Kb. Скачать 116.35 Kb.
|
Задание 6. Частный коэффициент корреляцииДля каждой пары показателей вычислить частный коэффициент корреляции и проверить его на значимость. Для значимых коэффициентов построить 95% доверительные интервалы. Сделать выводы. Формула частного коэффициента корреляции выглядит так: 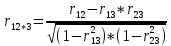 На таблице 10 изображены показатели частных коэффициентов. Таблица 10 – Частный коэффициент корреляции
𝑟12∗345 –частный коэффициент корреляции третьего порядка между x1 и x2 при исключении влияния x3, x4, x5. 1) r12*345= 0,44, можно предположить, что между выручкой от томатов и количеством посетителей имеется положительная и линейная зависимость при отсутствии влияния выручки от лапши, выручки от муки и выручки от крупы. 7) r13*245= 0,34, можно предположить, что между выручкой от лапши и количеством посетителей имеется положительная линейная зависимость при отсутствии влияния выручки от томатов, выручки от муки и выручки от крупы. 9) r14*235= 0,63, можно предположить, что между выручкой от муки и количества посетителей имеется положительная линейная зависимость при отсутствии влияния выручки от томатов, выручки от лапши и выручки от крупы. 10) r15*234= 0,58, можно предположить, что между выручкой от крупы и количеством посетителей имеется положительная линейная зависимость при отсутствии влияния выручки от томатов, выручки от лапши и выручки от муки. Проверим частные коэффициенты корреляции на значимость: Формула для проверки на значимость частных коэффициентов. В таблице 11 представлены показатели частных коэффициентов, проверенных на значимость. Таблица 11 – Проверка на значимость
Выдвигаем гипотезы:
Значимость полученных частных коэффициентов корреляции можно провести с использованием критерия Стьюдента. При этом проверяемая основная гипотеза 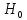 состоит в том, что истинный коэффициент корреляции равен нулю, т. е. состоит в том, что истинный коэффициент корреляции равен нулю, т. е. 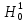 ∶ p_xixj=0 . Альтернативная гипотеза состоит в том, что истинный коэффициент корреляции не равен нулю: ∶ p_xixj=0 . Альтернативная гипотеза состоит в том, что истинный коэффициент корреляции не равен нулю: 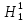 ∶ p_xixj≠0 . ∶ p_xixj≠0 . Далее сравниваем коэффициенты с критическим значением, 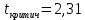 | 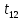 |> |>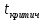 , значимый , значимый| 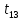 |> |>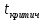 , значимый , значимый| 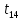 |> |>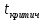 , значимый , значимый| 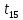 |> |>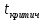 , значимый , значимыйТак как | 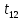 |> |>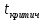 , следовательно с вероятностью 0,95 основная гипотеза , следовательно с вероятностью 0,95 основная гипотеза 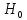 отвергается, значит частный коэффициент корреляции статистически значим, т.е. установлена линейная зависимость между количеством посетителей и выручки от томатов при исключении влияния выручки от лапши, выручки от муки и выручки от крупы. отвергается, значит частный коэффициент корреляции статистически значим, т.е. установлена линейная зависимость между количеством посетителей и выручки от томатов при исключении влияния выручки от лапши, выручки от муки и выручки от крупы.Так как | 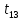 |> |>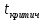 , следовательно с вероятностью 0,95 основная гипотеза , следовательно с вероятностью 0,95 основная гипотеза 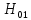 отвергается, значит частный коэффициент корреляции статистически значимт.е. установлена линейная зависимость между количеством посетителей и выручки от лапши при отсутствии влияния выручки от томатов, выручки от муки и выручки от крупы. отвергается, значит частный коэффициент корреляции статистически значимт.е. установлена линейная зависимость между количеством посетителей и выручки от лапши при отсутствии влияния выручки от томатов, выручки от муки и выручки от крупы.Так как | 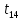 |> |>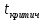 , следовательно с вероятностью 0,95 основная гипотеза , следовательно с вероятностью 0,95 основная гипотеза 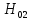 отвергается, значит частный коэффициент корреляции статистически значимт.е. установлена линейная зависимость между количеством посетителей и выручки от муки при отсутствии влияния выручки от томатов, выручки от лапши и выручки от крупы отвергается, значит частный коэффициент корреляции статистически значимт.е. установлена линейная зависимость между количеством посетителей и выручки от муки при отсутствии влияния выручки от томатов, выручки от лапши и выручки от крупыТак как | 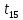 |> |>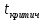 , следовательно с вероятностью 0,95 основная гипотеза , следовательно с вероятностью 0,95 основная гипотеза 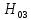 отвергается, значит частный коэффициент корреляции статистически значимт.е. установлена линейная зависимость между количеством посетителей и выручки от крупы при отсутствии влияния выручки от томатов, выручки от лапши и выручки от муки. отвергается, значит частный коэффициент корреляции статистически значимт.е. установлена линейная зависимость между количеством посетителей и выручки от крупы при отсутствии влияния выручки от томатов, выручки от лапши и выручки от муки.На таблице 12 изображены данные для построения доверительного интервала через Z. Таблица 12- Данные для построения доверительного интервала
Доверительный интервал имеет вид: 0,23 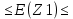 0,71 - для Z1 0,71 - для Z10,11 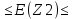 0,59 - для Z2 0,59 - для Z20,51 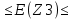 0,99 - для Z3 0,99 - для Z30,42 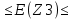 0,90 - для Z4 0,90 - для Z4Переход от Z к r (через решение уравнения): Таблица 13- Данные для построения доверительного интервала через r
где 𝑟𝑖𝑗𝑋(𝑖,𝑗) – частный коэффициент корреляции между x (i) и x (j) при фиксированных значениях всех остальных переменных X (i,j) , Тогда доверительный интервал имеет вид: 0,23 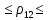 0,61 0,610,11 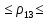 0,53 0,530,47 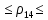 0,76 0,760,40 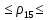 0,72 0,72Вывод: С вероятностью 0,95 значение коэффициент корреляции 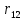 попадает в интервал от 0,23 до 0,61 попадает в интервал от 0,23 до 0,61С вероятностью 0,95 значение коэффициент корреляции 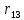 попадает в интервал от 0,11 до 0,53 попадает в интервал от 0,11 до 0,53С вероятностью 0,95 значение коэффициент корреляции 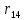 попадает в интервал от 0,47 до 0,76 попадает в интервал от 0,47 до 0,76С вероятностью 0,95 значение коэффициент корреляции 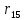 попадает в интервал от 0,40 до 0,72 попадает в интервал от 0,40 до 0,72 |