Контрольная работа по статистике. статистика кр. По данным табл. 1 необходимо
 Скачать 232.66 Kb. Скачать 232.66 Kb.
|
|
Задание 2. Имеются данные о распределении рабочих трех бригад по дневной выработке продукции (табл. 2). Вычислите: среднюю из групповых дисперсий, межгрупповую и общую дисперсии. Проверьте правильность расчетов с помощью правила сложения дисперсий. В незаполненные клетки внести число рабочих, соответствующее последней (*) и предпоследней (**) цифрам номера зачетной книжки. Таблица 2
Решение Проведем предварительные расчеты в таблице
а) Групповая дисперсия равна среднему квадрату отклонений отдельных значений признака внутри группы от средней арифметической этой группы. Внутригрупповые дисперсии вычисляются по формуле: Найдем средние по группам Первая: 44/12=62,5 Вторая 750/12=63,3 Третья 760/20=63,5 Внутригрупповые дисперсии: Первая группа:  Вторая группа:60027,7 Третья группа: 182728,7 б) Средняя из внутригрупповых дисперсий – это средняя арифметическая взвешенная из дисперсий групповых: 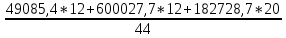 =112816,6 =112816,6в) Межгрупповая дисперсия равна среднему квадрату отклонений групповых средних от общей средней: 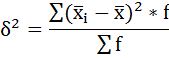 Общая средняя составила 63,18 Межгрупповая дисперсия 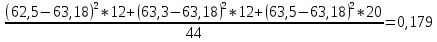 Общая дисперсия составила 112816,83. Проверим 0,179+112816,65=112816,83 Задание 3. На основании данных табл. 3 об объеме товарной продукции, произведенной предприятием в отчетном году, рассчитать систему следующих относительных показателей: планового задания, выполнения плана и динамики; структуры и координации, считая целым – объем товарной продукции, выпущенной фактически в отчетном году, а частями – объем продукции по видам; интенсивности, определив размер затрат на 1 руб. товарной продукции; сравнения объема товарной продукции, выпущенной предприятиями в отчетном году. Таблица 3
Решение а) Относительная величина планового задания показывает, во сколько раз намечаемый объем производства превысит достигнутый уровень или сколько процентов от этого уровня составит: где упл,0 – величина признака плановая и базисная. 68,5/65,9=1,039 Планом предусматривалось увеличить объем работ на 3,9%. Относительная величина выполнения плана (показатель выполнения плана) характеризует степень реализации плана. ОВВП = фактический уровень текущего периода / план текущего периода (28,5+40,7)/68,5=1,01 План реализован на 101% Относительная величина динамики (28,5+40,7)/65,9=1,045 Б) относительные показатели структуры Продукция А: 28,5/(28,5+40,7)=0,69 Продукция Б: 40,7/(28,5+40,7)=0,31 Относительный показатель координации 0,69/0,31=2,23 С) относительный показатель интенсивности 47,9/69,2=0,69 – затраты на 1 руб. товарной продукции Д) сравнения 68,0/69,2=0,98 Другое предприятие выпустило на 2% меньше продукции Задание 4. По данным табл. 4 рассчитать среднюю по трем предприятиям заработную плату за каждое полугодие. Охарактеризовать абсолютную и относительную динамику средней заработной платы. Отсчет 3 предприятий необходимо начинать с номера, соответствующего сумме двух последних цифр номера зачетной книжки студента. 2-4 Таблица 4
Решение: По формуле средней арифметической взвешенной определяем среднюю заработную плату в первом полугодии: х=∑хf∑f, где x - средняя заработная плата одного работника; f - численность работников. x0=(458*44000+450*45100+398*41190)/(458+450+398)=43522,7 руб. В январе средняя заработная плата одного работника составила 42295 руб. Определим среднюю заработную плату во втором полугодии 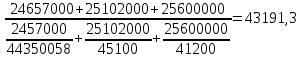 Абс. динамика средней заработной платы: 43191,3-43522,7=-331,36 Средняя заработная плата во втором полугодии уменьшилась на 331,36 Относ. Динамика средней заработной платы: 43191,3/43522,7=0,992 Средняя заработная плата во втором полугодии уменьшилась на 0,7%. Задание 5. Ввод в действие жилых домов предприятиями всех форм собственности в одной из областей в отчетном году характеризуется следующими данными, тыс. м2 общей площади: Таблица 5
Номер варианта определить по сумме двух последних цифр номера зачетной книжки. Для анализа ряда динамики определить цепные, базисные и средние: абсолютные приросты; темпы роста; темпы прироста; абсолютные значения 1% прироста. Рассчитать среднеквартальный объем ввода в действие жилых домов. Результаты расчетов оформить в таблице и сделать выводы. Решение
Базисные абсолютные приросты положительные в каждом квартале, что обуславливает темпы роста, которые по значению больше единицы. То есть, по отношению к базовому периоду мы наблюдаем рост квартальных объемов ввода. Что касается цепных темпов, то в четвертом квартале по отношению к третьему наблюдается снижение, поэтому темп роста цепной в этом периоде меньше нуля, а темп прироста имеет отрицательное значение. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
