Ответы на лабы по физике. Под светом в узком смысле
 Скачать 2.8 Mb. Скачать 2.8 Mb.
|
|
45 ОПРЕДЕЛЕНИЕ ПОСТОЯННОЙ СТЕФАНА - БОЛЬЦМАНА Что такое тепловое излучение, каков механизм его порождения, и почему тепловое излучение относят к квантово-оптическим явлениям? Одним из наиболее распространённых источников и механизмов порождения электромагнитного излучения является тепловое возбуждение атомов (молекул, ионов) вещества. При хаотическом тепловом движении, вследствие взаимодействий – “соударений”, часть атомов может переходить в возбуждённое состояние, характеризующееся избыточным, по сравнению с невозбуждённым состоянием, значением энергии. Возбуждённое состояние атома является неустойчивым, и он самопроизвольно переходит в более устойчивое – энергетически более низкое – состояние, избавляясь от избытка энергии путём излучения электромагнитных волн, которые и называют тепловым излучением. Интенсивность теплового излучения, очевидно, должно сильно зависеть от температуры, являющейся мерой теплового (внутреннего) движения атомов вещества. Кроме того, тепловое излучение твердых тел оказывается неравномерно распределенным по спектру3 частот (длин волн), который у твердых тел оказывается сплошным (непрерывным). Долгое время теоретики не могли получить (вывести) согласующийся с опытом характер распределения энергии теплового излучения идеализированного (абсолютно черного) тела по спектру длин волн. Наиболее серьезная попытка такого вывода, предпринятая Рэлеем и Джинсом, привела к формуле, которая решительно противоречила опыту в области коротких (ультрафиолетовых) волн. Возникшая «ультрафиолетовая катастрофа» указывала на неприменимость традиционных подходов классической (волновой) электродинамики и термодинамики к анализу такого микроскопического объекта, как тепловое излучение. Теоретическое устранение этой катастрофы потребовало перехода к новым, квантовым представлениям на свет. Дайте физический анализ основным характеристикам, задаче и законам теплового излучения: закону Кирхгофа, закону Стефана-Больцмана, закону смещения Вина, формуле Рэлея - Джинса. Важнейшей характеристикой в теории теплового излучения является излучательная способность (или излучательность) E,Т тела, представляющая собой спектральную плотность потока энергии теплового излучения, т. е. энергию, излучаемую телом в единицу времени с единицы площади в единичном интервале длин волн (или частот): E,Т = dE/(dSdtd). [Дж/(м2см) = Вт/м3] Т. к. = с/, то d = -сd/2 и от распределения излучательности по спектру длин волн можно перейти к распределению её по спектру частот: E,Т = E,Т 2/с, E,Т = E,Т с/2 = E,Т 2/с. Интегральную по всему спектру длин волн излучательную способность Энергетическая светимость абсолютно чёрного тела, в соответствии с геометрическим смыслом интеграла Важной характеристикой в теории теплового излучения является поглощательная способность ,Т тела, численно равная отношению поглощённого телом элементарного (в интервале длин волн от до + d) потока dФ погл к падающему на него элементарному потоку dФ пад излучения: ,Т = dФ, погл/dФ, пад (dФ, погл = dEпогл/(dtd). Поглощательная способность тела в состоянии равновесия всегда меньше единицы (в отличие от испускательной способности, она – безразмерна). Р. Кирхгоф установил важный закон в теории теплового излучения, отталкиваясь от такой его особенности, отличающей тепловое излучение от других видов излучения (например, от различных видов люминесценции), как способность находиться в равновесии со своим источником. В изолированной (замкнутой) системе, например в идеально отражающей полости, окружающей излучающее тело, его излучение со временем становится макроскопически определённым. Это значит, что распределение энергии по спектру со временем не меняется, и количество излучённой энергии в среднем должно быть равно количеству поглощённой энергии (для каждой частоты, направления распространения и поляризации). Поскольку излучение находится в равновесии (термодинамическом) с излучающим телом, можно говорить о температуре не только тела, но и самого излучения, считая их равными. Равновесный характер позволяет применить термодинамическое описание к тепловому излучению. Исходя из термодинамических соображений, Р. Кирхгоф в 1859 г. показал, что в состоянии термодинамического равновесия отношение излучательной и поглощательной способностей тел должно быть одинаковым для всех тел, независимо от их природы и конкретных особенностей, являясь функцией только температуры и частоты (длины волны): E,Т /,Т = (, Т), где (, Т) - универсальная (т. е. независящая от рода тела) функция длины волны и температуры, называемая функцией Кирхгофа. С  огласно закону Кирхгофа, тело, которое больше поглощает, должно и излучать больше. Особую роль в теории теплового излучения играет такая идеализированная модель, как абсолютно черное тело (а.ч.т.), которое полностью поглощает всё падающее на него излучение любых длин волн: для него ,Т 1. Близкой к единице поглощательной способностью обладает сажа ( 0,98), черный бархат ( 0,995). Технической моделью а.ч.т. является малое отверстие в полости с поглощающими стенками. Луч, вошедший в это отверстие, многократно отражаясь от стенок и поглощаясь ими, практически уже не выйдет из него, то есть полностью поглотится. В соответствии с законом Кирхгофа, для а.ч.т. E,Т = (, Т), т. е. излучательная способность абсолютно чёрного тела и есть универсальная функция Кирхгофа. Очередной шаг на пути решения основной задачи теории теплового излучения был сделан Стефаном в 1879 г, проанализировавшим накопленный экспериментальный материал и Больцманом в 1884 г, исходившим из термодинамических соображений. Они установили закон, названный их именами, связывающий энергетическую светимость (интегральную по всему спектру длин волн излучательную способность) EТ абсолютно черного тела с его температурой в четвёртой степени: Для равномерно излучающей черной поверхности в установившемся режиме EТ = Е/St = Р/S; отсюда энергия Е, излучаемая с поверхности S за время t равна: Е = Рt = EТSt = Т4St. Серое тело, у которого ,Т = Т = const 1, соответственно, излучает энергию W = ТТ4St В 1893 г Вин, исходя из термодинамических представлений, т. е. чисто феноменологически (внешне описательно), показал, что испускательная способность тел должна выражаться функцией вида Из формулы Вина для испускательной способности вытекало важное соотношение для длины волны м, соответствующей максимуму в спектре излучения тела. По условию экстремума, Согласно закону смещения Вина, максимум в спектре излучения а.ч.т. с ростом его температуры смещается в область более коротких волн. Физическая суть законов Стефана - Больцмана и смещения Вина довольно прозрачна. С ростом температуры возрастает интенсивность теплового движения атомов излучающего тела и интенсивность их теплового возбуждения, т. е. возрастает частота и высота уровней заброса электронов в атомах на возбуждённые орбиты (энергетические состояния). Обратные переходы электронов вниз и порождающие тепловое (электромагнитное) излучение, происходят с ростом температуры всё чаще и со всё более высоких орбит, соответствующих большим энергиям и частотам (Е = h) излучения. Поэтому с ростом температуры энергия излучения быстро растёт (пропорционально Т4), а максимум излучения смещается в область всё более высоких частот , то есть более коротких длин волн = с/. В 1900 г Релей, а затем и Джинс (1905 г) получили строго теоретически вид универсальной функции Кирхгофа, дающей распределение энергии в спектре излучения абсолютно чёрного тела. Тепловое излучение было рассмотрено на примере совокупности стоячих волн (осцилляторов) в полости с идеально отражающими стенками – в резонаторе. Расчет числа dn стоячих электромагнитных волн, заключенных в единице объема полости, длины волн которых заключены в интервале от до + d, дает значение dn = (2с/4)d. Применив классический закон о равномерном распределении энергии по степеням свободы (ЗРРЭСС), они приписали каждому собственному колебанию (моде) резонатора энергию, равную kТ (по kТ/2 на электрическую и магнитную составляющие электромагнитного колебания). Соответственно для спектральной плотности потока энергии излучения, т. е. для излучательной способности абсолютно черного тела, Релей и Джинс получили выражение: E,Т = (2с/4)kТ. Ф 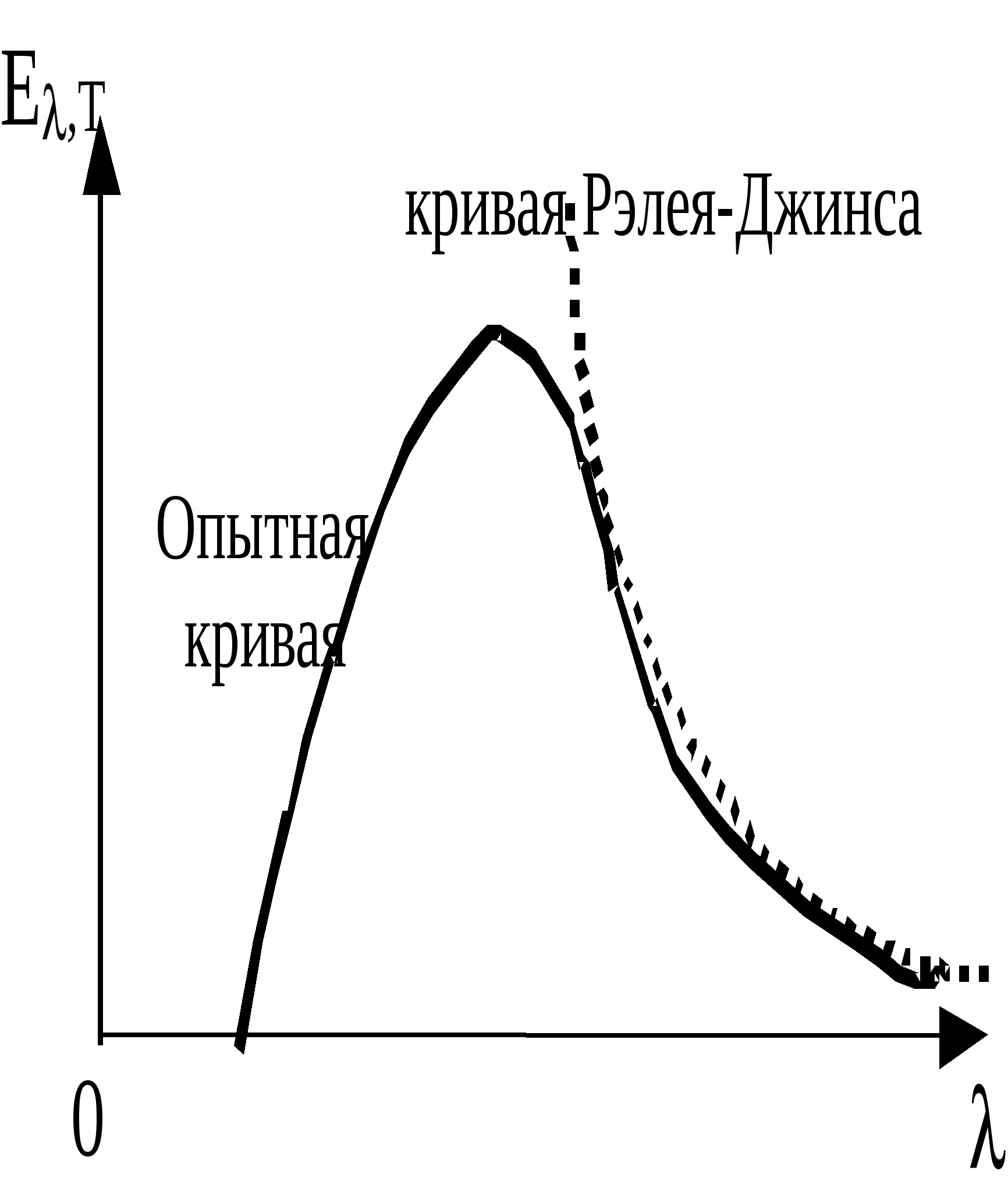 ормула Релея - Джинса хорошо соответствовала эксперименту в области больших длин волн, но имела значительное расхождение с ним в области коротких волн, соответствующих, например, ультрафиолетовому диапазону. Это несоответствие получило название ультрафиолетовой катастрофы. Катастрофы потому, что формула была получена в строгом соответствии с основными законами классической физики и, в частности, с законами классической статистики и волновой электромагнитной теории света, излучения. Стало очевидно, что эти основы классической теории не в состоянии адекватно отобразить новые экспериментальные факты. Возникла революционно-проблемная ситуация в фундаментальных основах классической теоретической физики. Первый шаг в переходе от классической к современной физике был сделан М. Планком в конце 1900 г. Что такое фотоны, и как гипотеза, и формула Планка позволяют получить и объяснить основные законы теплового излучения? Для устранения ультрафиолетовой катастрофы Планк вынужден был сделать чуждое классической физике предположение о том, что энергия осциллятора может принимать не непрерывный, а дискретный ряд значений, кратных некоторому кванту энергии, пропорциональному частоте колебаний: Е = h, где h = 6,6210-34 Джс - постоянная Планка. Это число формальное предположение, названное квантовой гипотезой Планка, устраняло ультрафиолетовую катастрофу тем, что в области высоких частот (высоких энергий Е = h) отсекало колебания, т. к. на их возбуждение не хватало энергии kT теплового движения атомов излучающего тела. Колебания с высокими частотами оказывались как бы замороженными, не возбуждаемыми и не вносящими вклад в энергию теплового излучения. По статистике Больцмана среднее значение Е энергии классического осциллятора, энергия Е которого обладает непрерывным спектром, равно: Е = 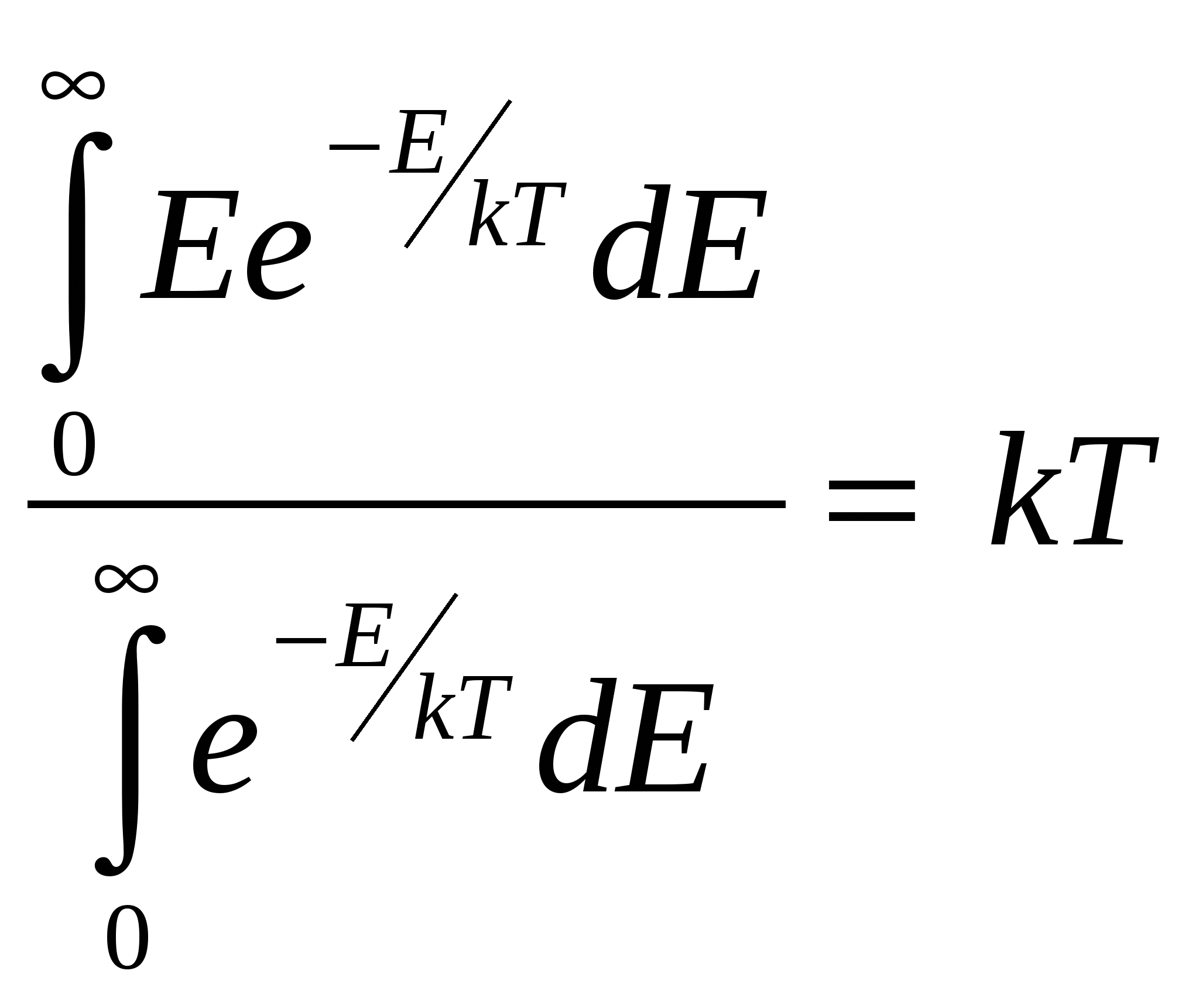 . . Для квантового осциллятора, энергия которого принимает дискретные значения nЕ, интегрирование необходимо заменить суммированием: 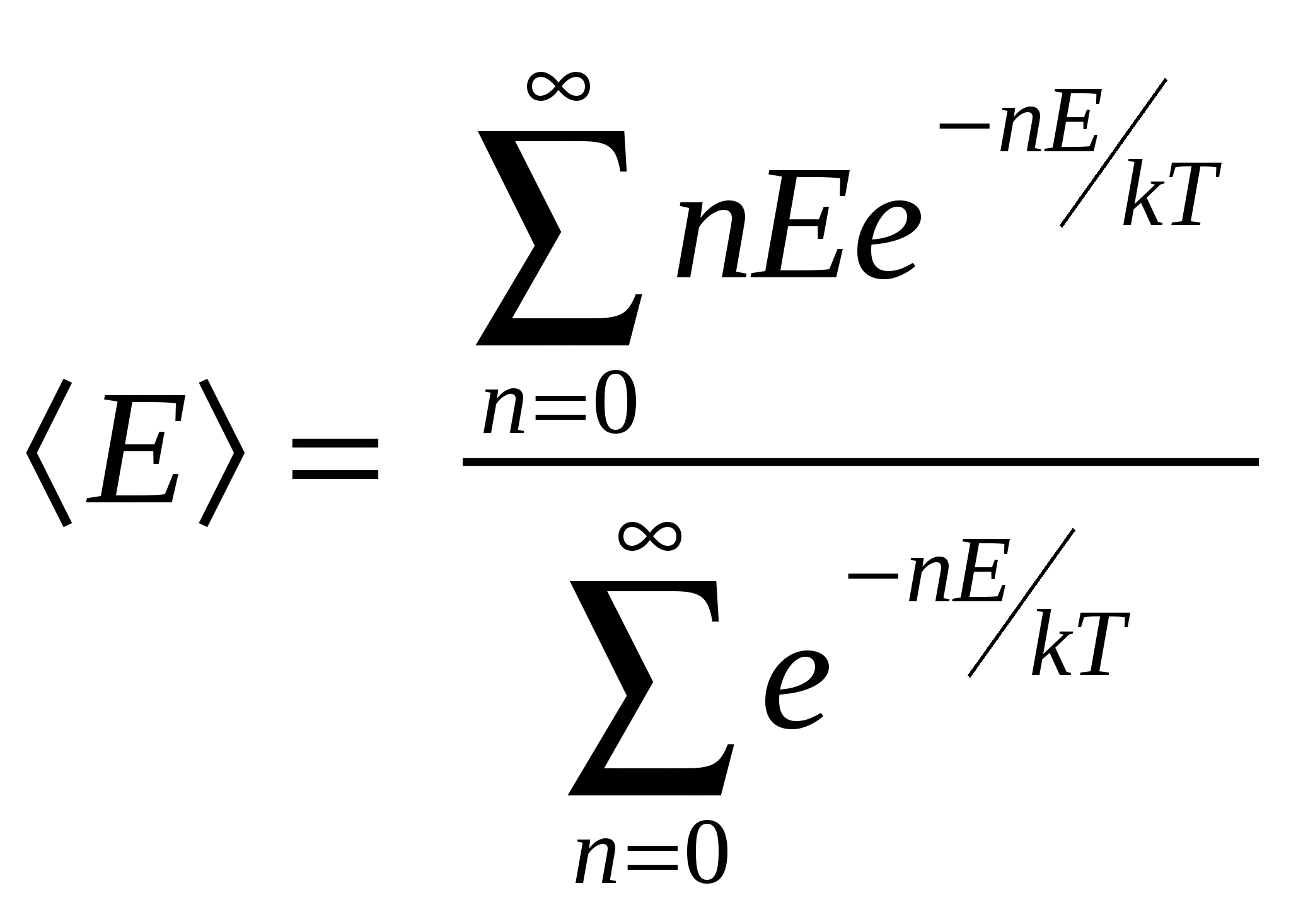 . Обозначая . Обозначая 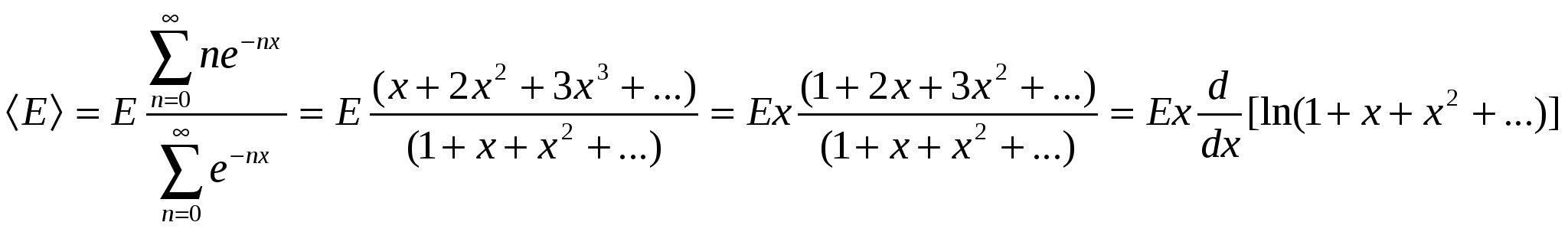 Аргумент логарифма – (1 + х + х2 + …) представляет собой геометрическую прогрессию с множителем равным х, сумма членов которой равна 1/(1 - х). Подставляя это выражение в формулу для Е, имеем: 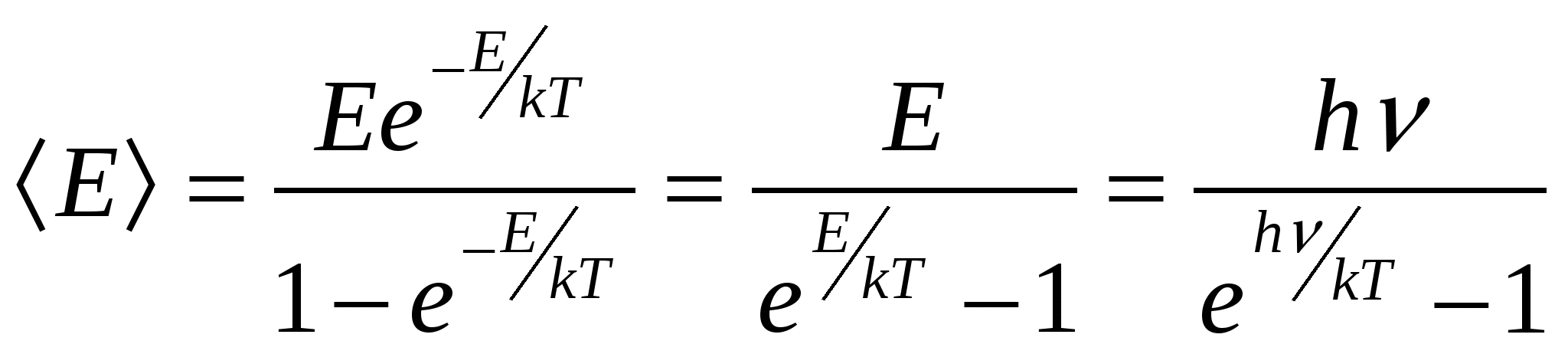 Заменяя в формуле Релея - Джинса классическое значение средней энергии Е = kT на квантовое Е = 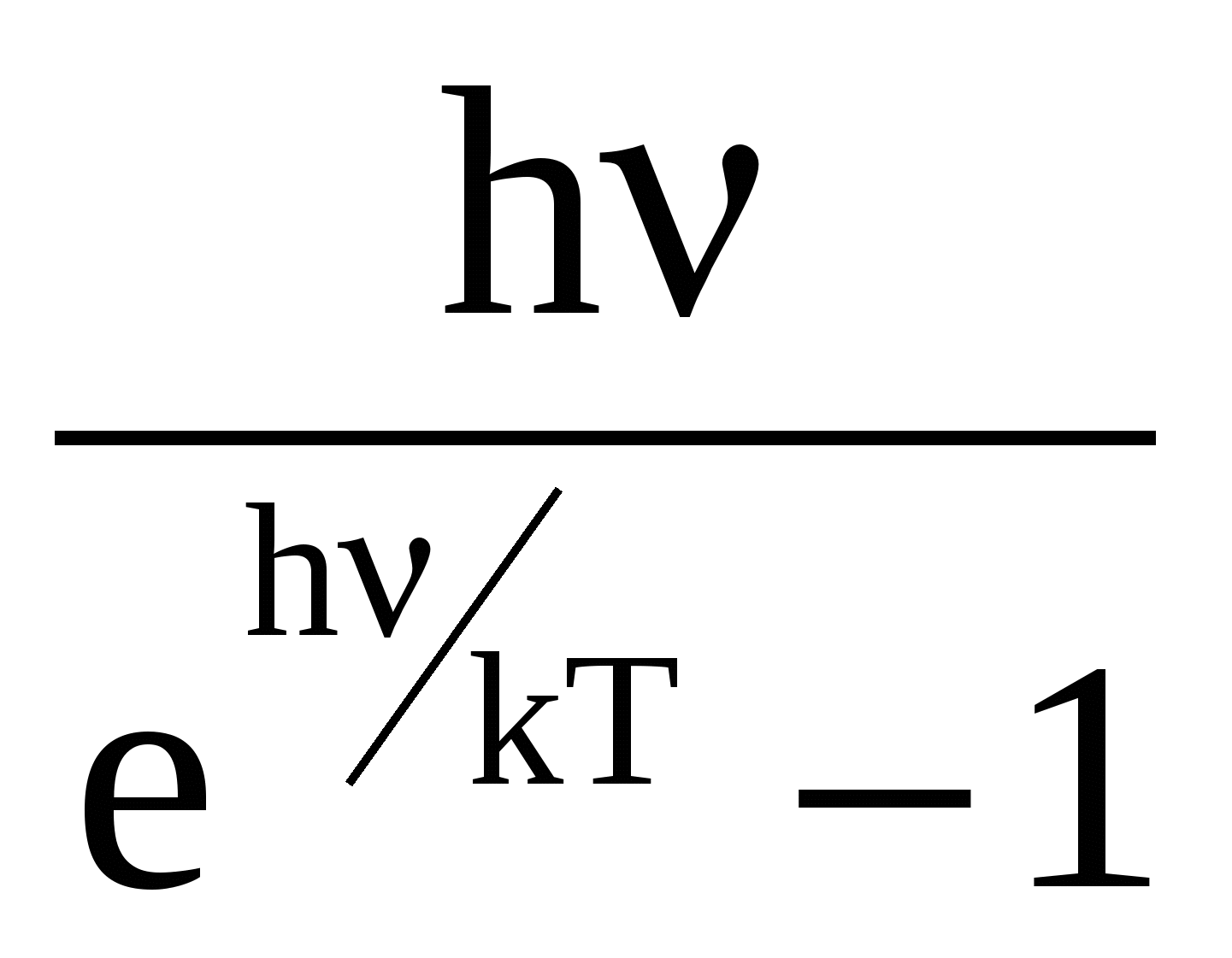 , получаем для излучательной способности формулу Планка: , получаем для излучательной способности формулу Планка:  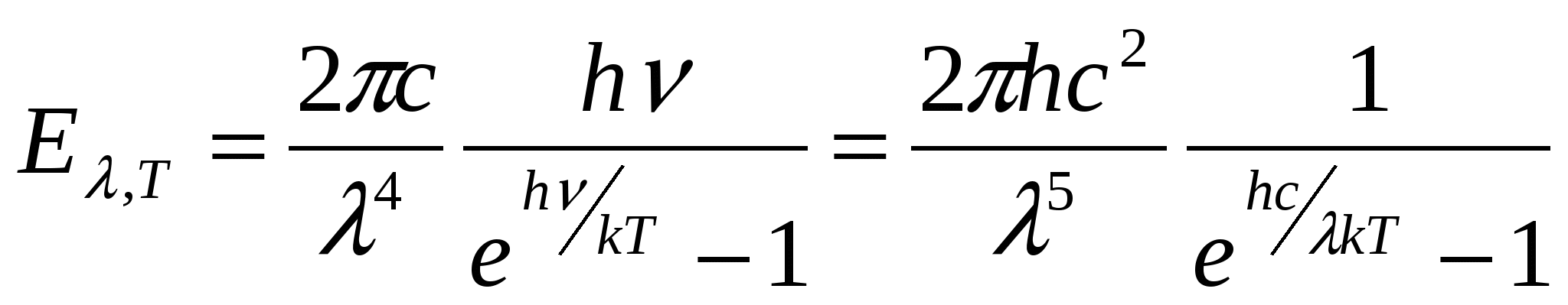 График спектра теплового излучения, даваемый формулой Планка, в точности совпадает с соответствующей экспериментальной зависимостью. Из формулы Планка вытекает формула Релея-Джинса, как её длинноволновое приближение: при  или или С увеличением длины волны (уменьшением частоты = с/) уменьшается энергия квантов света и резко понижается спектральная плотность их числа. В области больших длин волн и малых частот энергия h кванта ничтожна, и дискретный, квантовый характер излучения нивелируется, не проявляется В областях малых длин волн, то есть при приближение, отображаемое формулой Вина. Для интегральной излучательной способности (энергетической светимости) EТ получаем закон Стефана - Больцмана: 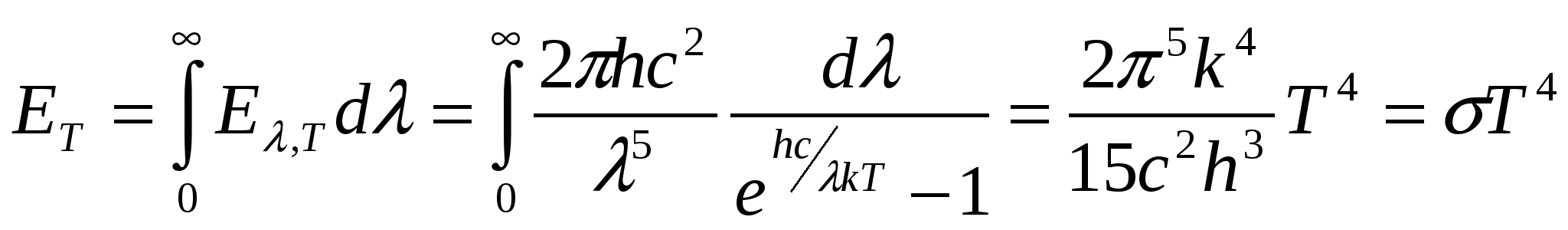 , , где = 25k4/15с2h3 = 5,6710-8 Вт/(м2К4). И, наконец, закон смещения Вина получается из формулы Планка при исследовании её на экстремум: Таким образом, М. Планком в 1900 г. было введено новое, непривычное для классической физики представление о квантах энергии электромагнитного излучения, позволившее целостно объяснить всю известную совокупность опытных фактов теплового излучения тел. Какие физические идеи и закономерности лежат в основе метода определения яркостной температуры в данной работе? Для определения постоянной Стефана-Больцмана, исходя из закона Стефана-Больцмана, необходимо знать температуру тела. Ее определение в данной работе осуществляется с помощью специального прибора – пирометра с исчезающей нитью. Он определяет так называемую яркостную температуру тела, в качестве которого в работе используется металлическая пластина, нагреваемая электрическим током. Пирометр содержит металлическую спираль, также нагреваемую электрическим током, регулируемым с помощью кругового реостата. Изменяя с помощью этого реостата ток накала нити пирометра, меняем температуру ее нагрева. Соответственно шкалу потенциометра (и пирометра в целом) можно проградуировать в единицах температуры. Такая градуировка производится с помощью уравнивания яркостей нити пирометра с яркостью эталонного (абсолютно черного) тела. Для этого сравнения пирометр снабжен оптической системой, позволяющей фокусировать изображение располагаемого перед пирометром эталонного (и/или исследуемого) нагретого тела в плоскость нити накала пирометра. При уравнивании с помощью регулировки круговым реостатом яркостей нити накала и нагретого тела происходит как бы растворение и исчезновение изображения нити накала пирометра на фоне изображения нагретого тела. Если исследуемое тело не абсолютно черное, пирометр покажет его яркостную температуру, которая оказывается заниженной, в сравнении с истинной. Как и почему взаимосвязаны яркостная и истинная температуры тела? Под яркостной температурой, по определению, понимают такую температуру тела, при которой его яркость в некотором узком интервале длин волн (задаваемом соответствующим светофильтром) равна яркости абсолютно черного тела. Так как абсолютно черное тело излучает больше энергии, то реальное (нечерное) тело должно иметь истинную температуру выше, чем черное тело. Поэтому истинная температура тела оказывается большей его яркостной температуры. Различие этих температур учитывается некоторым поправочным коэффициентом Z, значение которого зависит от поглощательной способности реального тела. Какой физический смысл имеет постоянная Стефана – Больцмана, и какова идея ее опытного определения? Коэффициент пропорциональности в законе Стефана-Больцмана ЕТ = Т4, называемый постоянной Стефана – Больцмана, численно равен: = 5,6710-8 Вт/(м2К4). Это значение равно мощности теплового излучения, испускаемого с единицы площади абсолютно чёрного тела при единичной температуре во всём диапазоне длин волн. Метод определения постоянной Стефана – Больцмана в данной работе основан на использовании условия энергетического баланса-равновесия: Р = Ризл - Рпогл нагреваемой электрическим током пластинки. Мощность электрического тока Р = UI, подводимая к пластинке, в состоянии равновесия равна разности мощностей Ризл - Рпогл, где Ризл = Т4S – мощность, отдаваемая пластинкой на тепловое излучение, а Рпогл = То4S – мощность поглощаемая пластинкой из окружающей среды, температура которой То. Из условия энергетического равновесия пластинки следует расчетная формула для постоянной Стефана-Больцмана: = UI/(Т4 - То4)S. 7. Охарактеризуйте полученные в работе результаты и оценку их точности. Работа № 46 Изучение законов фотоэффекта 1. Что такое фотоэффект, и каким образом свет вызывает вырывание электронов из вещества? Фотоэлектрическим эффектом или просто фотоэффектом называют совокупность электрических процессов, происходящих в веществе под воздействием света и включающую в себя внешний фотоэффект, внутренний фотоэффект и вентильный фотоэффект. П 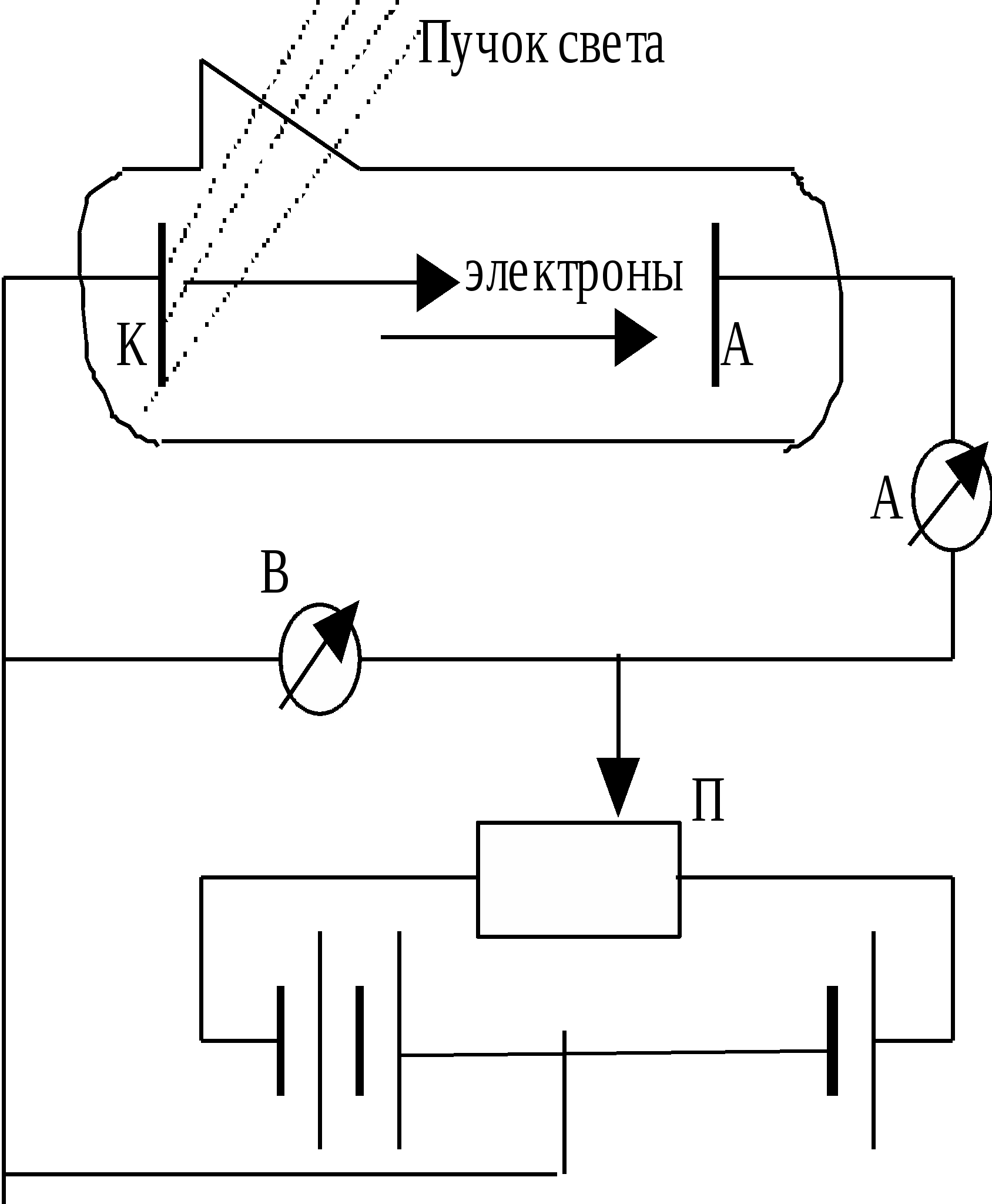 ервое фотоэлектрическое явление – внешний фотоэффект, заключающееся в вырывании светом электронов из вещества, впервые экспериментально было обнаружено в 1887 г. Г. Герцем и детально исследовано в 1888 - 1889 гг. А. Г. Столетовым. Падающий на катод свет своим переменным электрическим полем раскачивает электроны, и, при некоторых условиях, происходит отрыв электронов от вещества и вылет их из катода. 2. Каковы основные закономерности внешнего фотоэффекта? Обобщённая схема экспериментальной установки для изучения внешнего фотоэффекта (см. рис) представляла собой двухэлектродную стеклянную трубку, лампу (вакуумный диод - фотоэлемент), один из электродов (катод К) которой облучался пучком света. Между катодом и вторым электродом – анодом А прикладывалось напряжение U, которое можно было регулировать (как по величине, так и по знаку, полярности) с помощью потенциометра П. Амперметр А измерял силу I тока, протекающего через лампу, а вольтметр В измерял напряжение между анодом и катодом. В силу имеющегося разброса начальных скоростей электронов, вылетающих из разных по глубине слоев вещества катода, до анода долетают лишь наиболее быстрые из них. С ростом положительного напряжения на аноде число таких электронов возрастает, и при некотором напряжении все, вырванные светом из катода электроны, достигают анода, образуя ток насыщения нас. Чтобы обратить фототок в ноль, необходимо между анодом и катодом приложить напряжение Uз обратной полярности, называемое задерживающим или запирающим. Оно определяется из условия равенства кинетической энергии Ек фотоэлектрона работе А = qеUз задерживающего электрического поля по торможению электрона, то есть из равенства: Ек = qеUз. Х 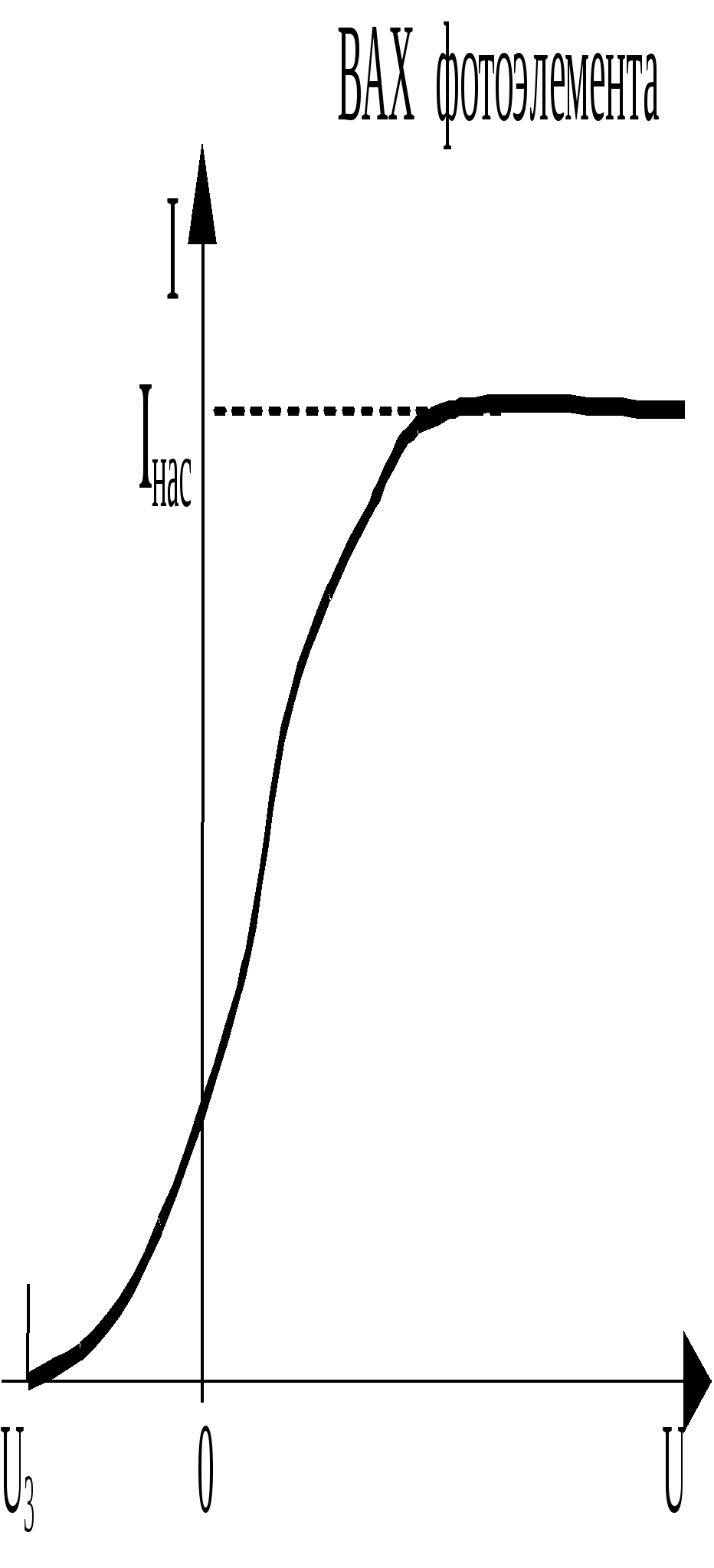 арактерные особенности внешнего фотоэффекта наиболее полно вскрываются в его вольтамперной характеристике (ВАХ), представляющей собой зависимость силы фототока (тока электронов, попадающих на анод) от напряжения между катодом и анодом (катодом является облучаемый светом материал). Опыты выявили следующие основные закономерности внешнего фотоэффекта: 1. Сила тока насыщения нас прямо пропорциональна световому потоку4 Ф: нас Ф (эта закономерность носит название закона Столетова). 2. Фотоэффект начинается с некоторой минимальной частоты света мин (или о), получившей название красной границы5 фотоэффекта. 3. Максимальные кинетическая энергия Ек макс и скорость к макс фотоэлектронов (а также и задерживающее напряжение Uз) пропорциональны частоте света и не зависят от его интенсивности. 4. Фотоэффект практически безынерционен, т. е. фототок возникает мгновенно после облучения светом вещества. 3. Что в фотоэффекте и почему не смогла объяснить волновая теория света? Согласно классической волновой электромагнитной картине света, вырывание электронов, связанных в веществе, происходило вследствие возрастающей во времени “раскачки” их переменным электрическим полем световой волны. В волновом подходе интенсивность света пропорциональна амплитуде световой волны, и именно эти характеристики должны были определять возможность самого фотоэффекта и его “силу”. Опыт же говорил о том, что определяющей характеристикой оказывается частота света. Волновой подход не смог объяснить основные закономерности внешнего фотоэффекта и, прежде всего, частотные закономерности (наличие красной границы, пропорциональность запирающего напряжения частоте света), а также его безынерционность и независимость запирающего напряжения от интенсивности света. Свет оказался объектом (микрообъектом), к которому нельзя было применять законы классической (макроскопической) физики. Это несоответствие классической волновой теории и опыта было преодолено в 1905 г. А. Эйнштейном путем привлечения квантово-корпускулярных представлений о свете, предложенных в 1900 г. М. Планком при объяснении закономерностей теплового излучения. 4. Что такое фотоны, и почему фотоэффект относят к типично квантовым оптическим явлениям? Для объяснения выявленных в опыте закономерностей фотоэффекта А. Эйнштейн развил гипотезу М. Планка о квантах света, предположив, что свет не только излучается в виде дискретных энергетических порций, квантов, энергия Е которых пропорциональна частоте Е = h, но и поглощается веществом также этими неделимыми порциями света, названными впоследствии фотонами. Фотоэффект является квантовооптическим явлением потому, что в его основе лежит взаимодействие элементарных частиц – микрообъектов (фотона и электрона), адекватно описать которое классическая волновая теория света оказалась неспособной. Как с позиций уравнения Эйнштейна для фотоэффекта объясняются его основные закономерности? Эйнштейн записал основное уравнение однофотонного фотоэффекта, представляющее собой фактически закон сохранения энергии при взаимодействии фотона со связанным в веществе электроном. Согласно этому уравнению, энергия фотона h = Авых + Ек макс За работу Авых в уравнении Эйнштейна принимают работу по вырыванию наименее связанных в веществе электронов, которые приобретают при вылете наибольшую скорость и кинетическую энергию Ек макс. Из уравнения Эйнштейна сразу вытекает наличие красной границы фотоэффекта, т. е. существование такой граничной частоты о, при которой начинается фотоэффект и ниже которой энергии фотона не хватит на совершение работы выхода электрона, т.е. на преодоление сил связи его с веществом: hо = Авых о = Авых/h. о и Авых являются табличными характеристиками вещества. Задерживающее напряжение определяется из условия обращения фототока в ноль. При этом тормозящее электрическое поле между катодом и анодом совершает работу А, равную максимальной кинетической энергии электронов А = qеUз = Ек макс. Подставляя вместо Ек макс в уравнение Эйнштейна qеUз, имеем: h = Авых + qеUз, откуда Uз = (h - Авых)/qе Uз . Таким образом, из уравнения Эйнштейна логически вытекает пропорциональная зависимость задерживающего напряжения Uз (а с ним и максимальных кинетической энергии Ек макс и скорости фотоэлектронов к макс) частоте света при фотоэффекте и независимость Uз от интенсивности света. Интенсивность света в квантовом подходе оказывается пропорциональной числу фотонов, ежесекундно, падающих на единицу площади. Отсюда становится понятной пропорциональность силы фототока насыщения световому потоку6 Ф, облучающему материал. При фототоке насыщения все вырванные из материала электроны достигают противоположного электрода. В стадии до насыщения часть вылетевших из материала электронов, обладающих скоростью, меньше максимальной, возвращалась обратно под воздействием отталкивающего электрического поля ранее вылетевших электронов и притягивающего действия, положительно заряжающегося при отдаче электронов катода. С увеличением интенсивности света увеличивается число фотонов, ежесекундно бомбардирующих катод и, соответственно, число вырываемых ими электронов, которые в стадии насыщения все достигают анода, обусловливая возрастание силы тока насыщения. Безынерционность фотоэффекта в квантовом подходе тем и объясняется, что взаимодействие электронов со светом носит не растянутый во времени, как с волной, а элементарный, мгновенный характер взаимодействия двух частиц – частицы вещества и частицы света (электромагнитного поля) – фотона. 5. Какие физические идеи и закономерности лежат в основе метода исследования» используемого в данной работе? 6. Дайте объяснение полученным в работе результатам и зависимостям? Работа № 48 СПЕКТРЫ АТОМАРНЫХ ГАЗОВ 1. Каков механизм излучения света атомами и характер спектра излучения? Под действием внешнего электромагнитного излучения (света) атом может совершить вынужденный переход "вверх" - в возбужденное состояние с повышенной, энергией. При этом происходит поглощение атомом кванта падающего на него света, частота которого должна отвечать условию (правилу) частот Бора: Возбужденное состояние атома с повышенной энергией является нестабильным, и спустя довольно малое время атом избавляется от избытка ("груза") энергии, переходя в энергетически более "выгодное" (более низкое) состояние. Такой переход "вниз" обычно сопровождается излучением кванта света, фотона. Наблюдения спектров1 излучения (с помощью призменных или дифракционных спектроскопов) показали, что в атомарном, газообразном состоянии вещество обладает дискретным (линейчатым) спектром, как излучения, так и поглощения. Этот спектр является своего рода паспортом соответствующего химического элемента, то есть он индивидуален, неповторим для атома каждого химического элемента. Линии поглощения расположены в тех же местах спектра, в которых находятся линии излучения. Дискретный характер спектра атомов обусловлен тем, что энергия атома квантуется, то есть, принимает лишь определенные, квантованные значения. 2. Почему энергия электрона в атоме квантуется? Как это подтверждается экспериментом? Атом является квантовой системой. Движение электронов в нем пространственно ограничено, и их энергия (а с нею и энергия атома в целом) квантуется, то есть принимает дискретный ряд значений. Согласно квантовой механике, аналитически общие условия квантования энергии микрочастицы задаются как условия ее локализации (двухсторонней пространственной ограниченности области ее движения): Волновая функция (х) квадратом своего модуля |(х)|2 выражает плотность вероятности местонахождений частицы. Поэтому условие (х) 0 при х означает, что с ненулевой вероятностью частица обнаруживается в некоторой конечной, ограниченной области (между – и + ), которая и есть область ее локализации. |
