Ответы на лабы по физике. Под светом в узком смысле

• Название: Под светом в узком смысле
• Анкор: Ответы на лабы по физике.doc
• Дата: 11.05.2017
• Размер: 2.8 Mb.
• Имя файла: Ответы на лабы по физике.doc
• Тип: Документы; #7447
• Категория: Физика
• страница: 3 из 6

43_1-4 1. Что такое свет и какова необходимость введения и суть такой его ха­рактеристики, как поляри­зация?

Под светом в узком смысле (видимым светом) понимают электромагнитные волны с длинами в интервале (0,38 - 0,76) мкм, размещающем в себе "семь цветов радуги". В более широком смысле под светом понимают электро­магнитные волны с длинами, меньшими одного миллиметра. Электромагнитная волна - распространяющиеся в пространстве взаимно перпендикулярные колебания электрического и магнитного полей - описывается урав­нением бегущей (вдоль оси Z:   ) волны:

= cos (t - kz + ) и =cos (t - kz + )

На практике большинство оптико-волновых эффектов связано с электрическим полем,
и поэтому в дальнейшем рассматриваются колебания только электрического поля. В силу чрезвычайно высокой частоты  колебаний вектора в световой волне (  10¹⁵ с^-1) и инерци­онности оптических приборов (включая наш глаз), они не успевают реагировать на текущие, мгно­венные изменения электрического поля. Приборы регистрируют лишь ус­реднённый во времени поток энергии, пропорциональный квадрату амплитуды, называемый интенсивностью J (или освещенностью, или световым потоком) света: J   Е² (угловые скобки означают усреднение величины по времени).

Представляя собой поперечные электромагнитные волны, свет обладает внутренней харак­теристикой, называемой поляризацией, отражающей возможность какого-либо упорядочения колебаний вектора (и, соответственно, вектора ) в плоскости перпендикулярной направлению распространения (вектору скорости ) волны.

2. Охарактеризуйте виды поляризации света и их взаимосвязь, взаимо­представления.

Свет называется полностью поляризованным, если две взаимно-перпендикулярные компо­ненты (проекции) век­тора светового пучка совершают колебания с постоянной во времени раз­ностью фаз. В общем случае проекция конца вектора такого света на плоскость перпендику­ляр­ную на­правления его распространения, описывает эллипс. Такой свет называют эллиптически поляризованным (ЭПС).

Большой интерес представляют предельные случаи эллиптической поляризации: 1) линейная, когда эллипс выро­ждается в отрезок прямой линии и 2) циркулярная (или круго­вая), когда эллипс переходит в окружность.

Е

стественный свет является неполяризованным. Он не обнаружи­вает фазовой корреляции между компо­нентами вектора ; разность фаз между ними непрерывно хаотически меняется и вектор с течением вре­мени рав­новероятно и неупорядо­ченно занимает любые направления (в плоскости перпендикулярной век­тору скорости волны).

Между видами поляризованного света существует взаимосвязь. Так, циркулярно или эллиптически поляризованный свет (ЦПС и ЭПС), можно разложить на две линейно поля­ризованные во взаимно-перпендикулярных направлениях световые волны с одинаковой частотой и разностью фаз в 90:

Е₁ = Е_м1 sin (t – kх) и Е₂ = Е_м2 cos (t – kу).

П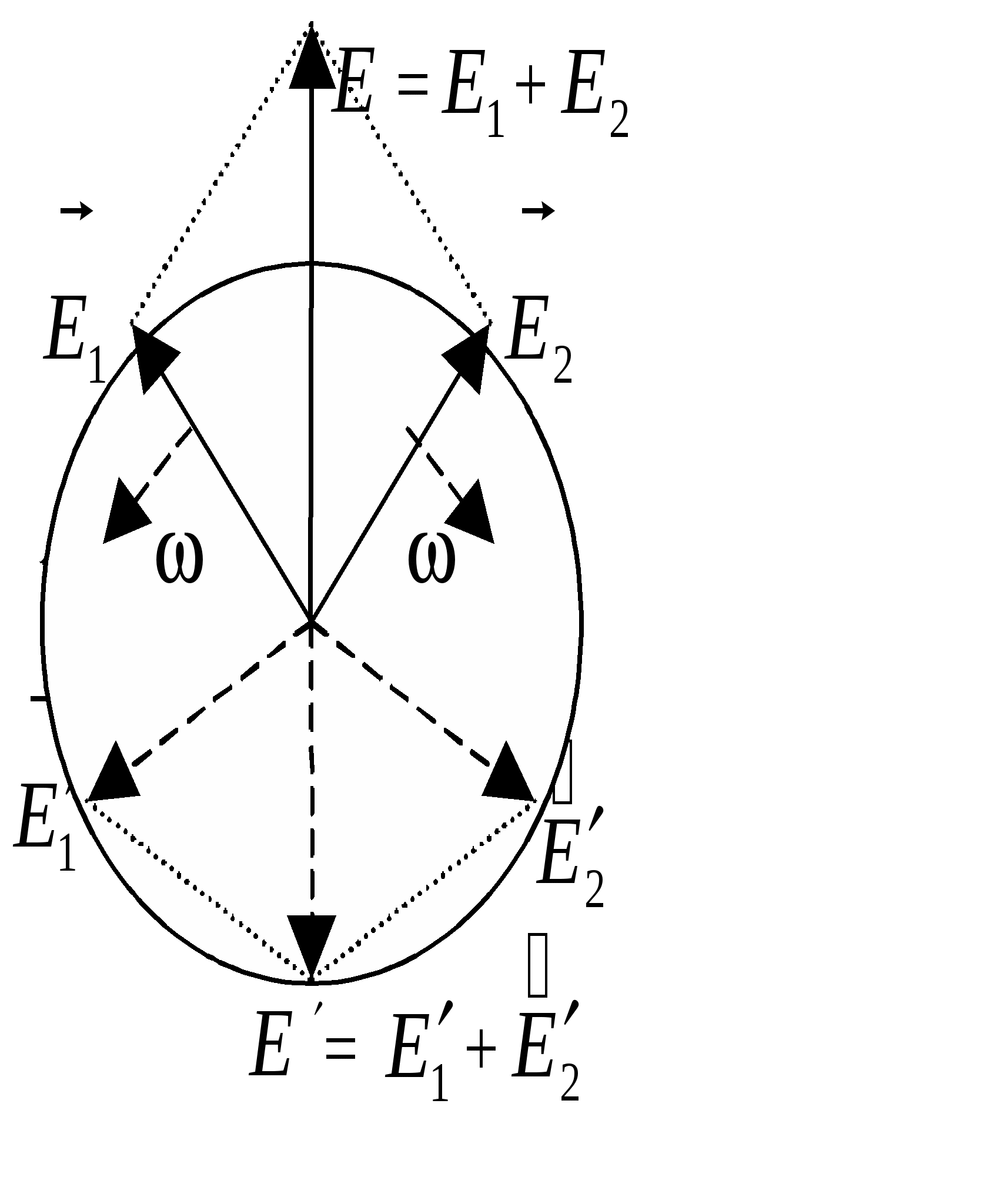


одобная взаимосвязь рассматривалась в механике, в задаче о сложении взаимно-перпендику­лярных колебаний одинаковой частоты. Если амплитуды Е_х = Е₁ и Е_у = Е₂ складываемых волн (колеба­ний) равны, то результирующее колебание оказывается циркулярно-поляризованным, в других же случаях – эллиптически поляризованным.

Линейно-поляризованный свет (ЛПС), в свою очередь, можно разложить на две циркулярно (или эллиптически) поляризованные волны, векторы которых вращаются с одинаковой скоростью  в противопо­ложных направлениях.

Поляризация света может быть частичной, когда фазовый сдвиг между взаимно перпенди­куляр­ными компонентами вектора световой волны имеет некоторое преимущественное значение. Если оно равно нулю, свет называется частично линейно поляризованным, если же оно равно /2, имеем час­тично циркулярно-поляризованный свет.

Величина Р степени поляризации света, опреде­ляемая как отношение разности интенсив­ностей J₁ – J₂ двух выделенных взаимно перпендикулярных компонент к их cyммe J₁ + J_2, то есть: Р = (J₁ – J₂)(J₁ – J₂), может ме­няться в пределах от 0 % (неполяризованный свет) до 100 % (полностью поляризованный свет).
3. Охарактеризуйте методы получения поляризованного света и дайте вывод закона Малюса.

Устройства, служащие для получения линейно поляризованного света из неполяризован­ного, называ­ются поляризаторами. Поляризатор обладает способно­стью пропускать свет с колеба­ниями вектора , парал­лельными некоторой плоскости, называемой плоскостью поляризатора. Т. к. в естественном свете колебания вектора всегда могут быть представ­лены в виде суммы двух равноправных взаимно перпендикулярных компонент, то поляризатор, про­пустив лишь компо­ненту параллельную своей плоскости, вдвое уменьшает интенсивность падающего на него естест­венного света, делая его линейно поляризован­ным.

Е


сли же на поляризатор падает линейно поляризованный свет (по­ляризатор в этом случае называют анализатором), то на выход проходит компонента _//, параллельная плоскости анализа­тора М: Е_// = Е_оcos , гдe  - угол между вектором _о падающего на анализатор ЛПС и плоскостью анализатора. Интенсивность же ЛПС на выходе анализатора:

J_вых =  Е_//² = Е_о²cos²  = J_оcos² .

Соотношение J_вых = J_оcos² , связывающее интенсивности ЛПС
на выходе и входе анализатора с углом между вектором _о и плоскостью анализатора, называется законом Малюса.

Если на вход системы из поляризатора и анализатора, угол между плоскостями которых равен , падает естественный свет с интенсивностью J_ест, то интенсивность J_вых линейно-поляризо­ванного света на выходе системы будет равна: J_вых = (12)J_ест cos² .
4. Дайте детальный физический анализ закону Брюстера.

Если на границу раздела двух сред с показате­лями преломления n₁ и n₂, падает пучок естественного света под таким углом _Б, при котором tg _Б = n₂n₁, то, согласно закону Брюстера, от­раженный луч оказыва­ется полностью линейно поляризованным в плоскости перпендикулярной плоскости падения. Пре­ломленный луч оказывается при этом частично (но наи­более) поля­ризован­ным, а угол между отраженным и преломлен­ным лучами составляет 90°.

В


естественном свете содержится равное количе­ство колебаний вектора , происходящих в плоскости паде­ния (обозначаемых /) и в перпендикулярной ей плоскости (обозначенных ). Отра­женный луч, как правило, состав­ляет по интенсивности (4 - 7) % от падающего луча и уносит лишь незначительную часть всех колебаний век­тора , совершающихся в плоскости перпендикулярной плоскости падения. Поэтому в преломленном луче поля­ризация оказыва­ется частичной; в нем лишь незначи­тельно преобладают колебания, совершающиеся в плос­кости паде­ния над перпенди­кулярными им колебаниями.

Простейшее физическое истолкование закона Брюстера состоит в следующем. Электриче­ское поле падающей световой волны вызывает в диэлектрике (во 2-ой среде) колебания электронов, направ­ление которых совпадает с направлением вектора во второй среде (в преломленной волне). Эти ко­лебания возбуждают на поверхности раздела сред отраженную волну. Но линейно колеб­лющийся электрон не излучает в направлении своих колебаний. Таким образом, в отраженной волне колебания электриче­ского поля происходят только в плоскости, перпендикулярной плоско­сти падения.

Перпендикулярность отраженного и преломленного лучей вытекает из формул закона Брюстера и закона преломления света:

t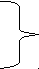g _Б = sin _Бcos _Б = n₂n₁

 sin  = cos _Б   + _Б = 2

sin _Бsin  = n₂n₁  =  - ( + _Б) = /2
Существуют среды, называемые анизотропными, в которых значение показателя преломле­ния оказывается разным для разных направлений колебаний вектора . При падении света (как естественного, так и линейно поляризованного) на анизотропный кристалл преломленный луч в нем раздваивается на два (обыкновенный и необыкновенный), которые оказываются линейно поля­ризованными во взаимно перпендикулярных направлениях.

Если длина кристалла равна /4, разность фаз обыкновенного и необыкновенного лучей
на выхода равна 2 (если на выходе был ЛПC), и складываясь, они дают свет, поляризованный
по эллипсу (ЭПС) (естественный же свет, падающий на кристаллическую пластинку в /4, после ее прохождения остается естественным).

Путем некоторой ориентации кристаллической «/4» пластинки относительно вектора
в падающем на нее ЛПС, можно добиться равенства амплитуд обыкновенного и необыкновенного лу­чей. Тогда их сумма на выходе пластинки дает свет, поляризованный по кругу (ЦПС).

Различие показателей преломления приводит к разли­чию скоро­стей вращения ₁ и ₂ векторов ₊ и 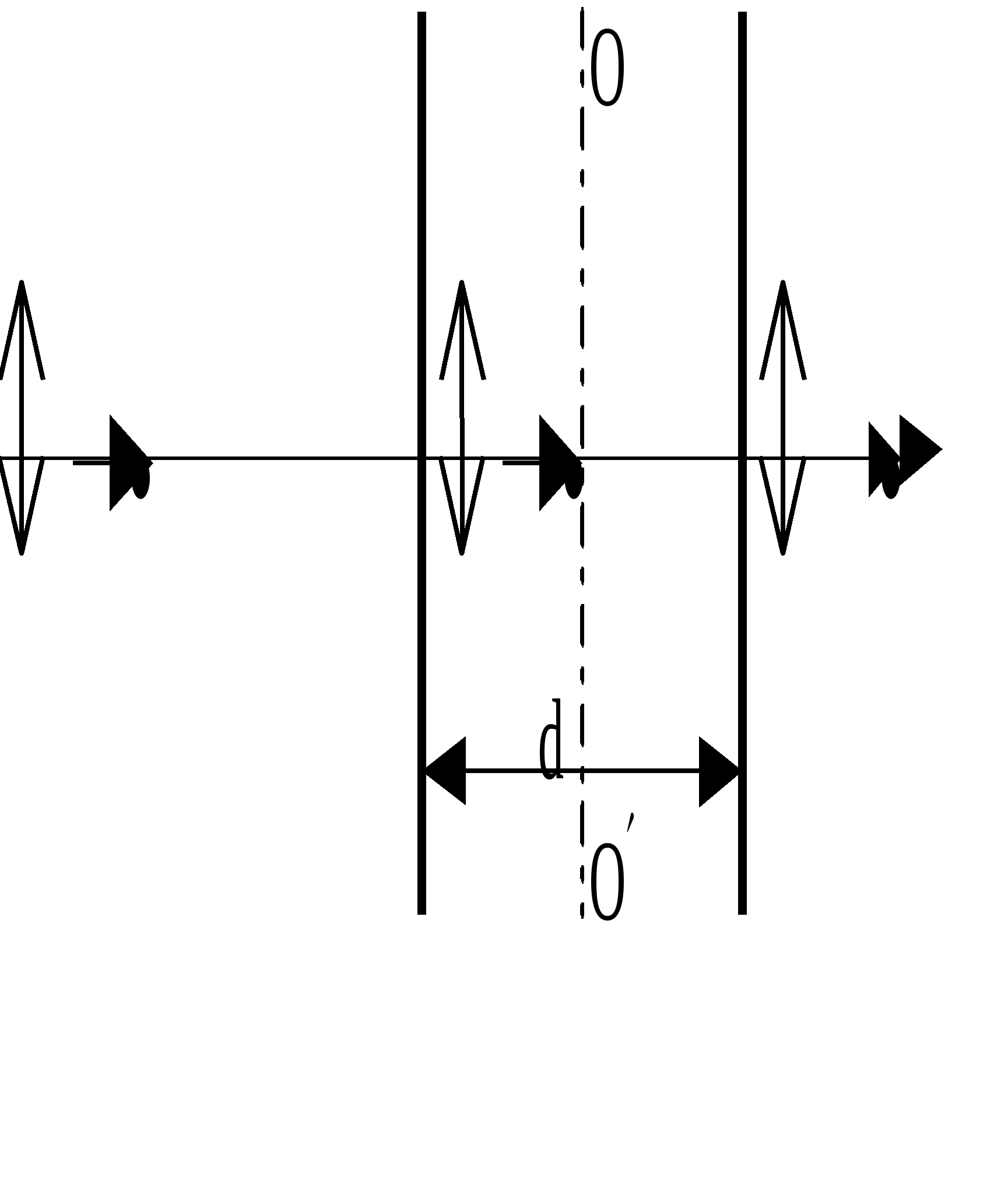_- и к возрас­тающему откло­нению с течением времени на угол  резуль­тирующего колебания вектора от первоначального на­правления.

П


усть из одноосного кристалла выре­зана пластинка, оптическая ось ОО^ которой парал­лельна поверхности кристалла и пусть на пла­стинку сверху нормально падает свет. В кристалле (пластинке) лучи пойдут без пре­ломления, не раздваиваясь на обыкновенный и необыкновенный лучи, но с разными скоростями: _о = с/n_о и _е = с/n_е. В результате, по выходе из кристалла, обыкновенный и необыкновенный лучи со вза­имно перпендикулярными поляризациями приобретут разность хода  = (n_о – n_е)d: и, соответст­венно, разность фаз Ф = (2_о)(n_о – n_е)d.

При  = m_о + _о4, где m  , Ф = 2m + 2, пластина называется пластинкой в четверть волны, а при  = m_о + _о2 пластинкой в полволны. Если пластинку в четверть волны поставить на пути эллиптически (или циркулярно) поля­ризованного света и ось кристалла направить параллельно оси симметрии эллипса, то из пластинки выйдет линейно поляризованный свет. На этой особенности основан метод различения эллиптиче­ски поляризованного света от частично поляризованного и циркулярно поляризованного света от естественного света.

Пластинка в четверть волны может превратить эллиптически поляризованный свет (вклю­чая, естественно и циркулярно поляризованный - как частный случай эллиптически поляризован­ного света) в линейно поляризованный свет, но она не меняет поляризации частично поляризован­ного света и естественного света.

Некоторые вещества, называемые оптически активными, обладают способностью поворачи­вать плоскость поляризации (плоскость векторов и скорости волны), проходящего через него линейно поляризованного света. Так например, в системе из скрещенных поляризаторов (николей) помещение пластинки кварца между ними с оптической осью 00', не вызывающей расщепления обыкновенного и необыкновенного лучей, вызывает просветление экрана. Мера этого просветления зависит от длины волны света и толщины пластинки. Это явление было объяснено тем, что кварц поворачи­вает плоскость поляризации вышедшего из первого поляризатора линейно поляризованного света. И на выходе кварцевой пластинки плоскость поляризации света оказывается уже не перпендику­лярной направлению пропускания второго поляризатора, и часть света будет пропущена на выход системы, на экран.

Опытным путём было выявлено, что угол  поворота плоскости поляризации оптически
активным веществом, проходящего через него линейно поляризованного света, прямо пропорцио­нален толщине d пластинки:  = _оd, где _о - постоянная, называемая удельным вращением, изме­ряется в градусах на миллиметр и зависит от длины волны, рода вещества, температуры. Для растворов оптически активных веществ:  = [_о]сd, где с - концентрация раствора, [_о] - постоянная вращения, зависящая также от , Т и рода вещества.

Ф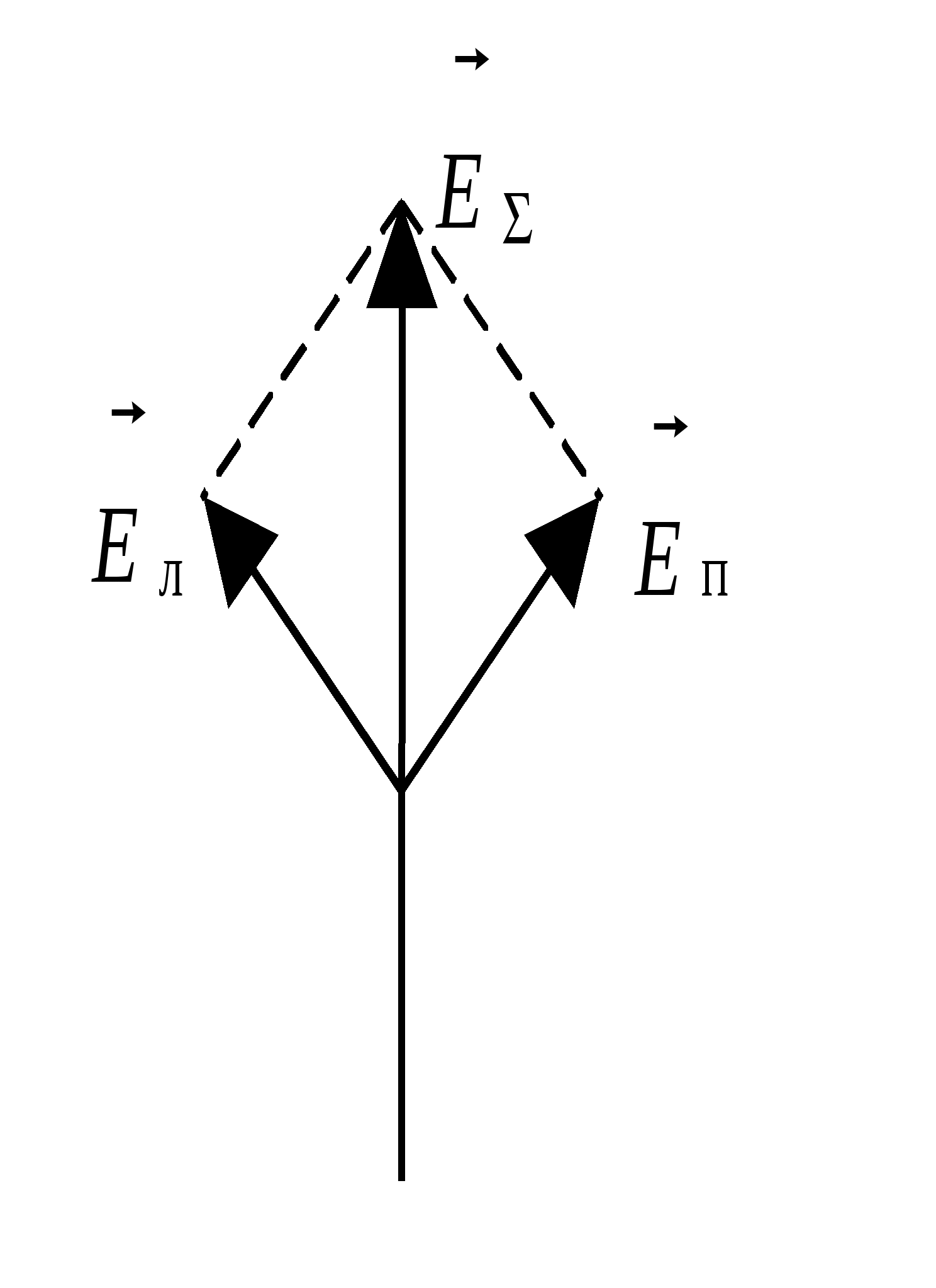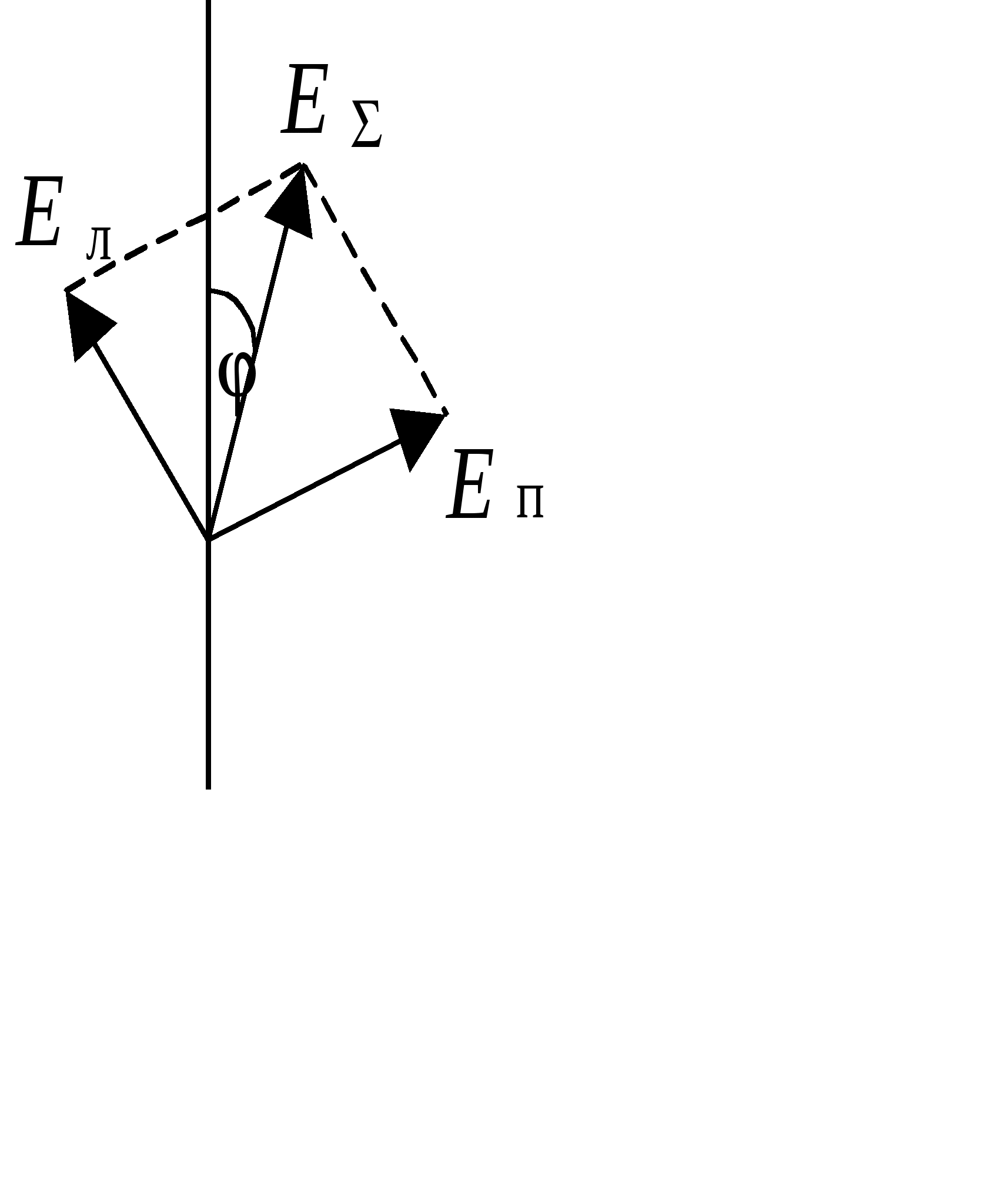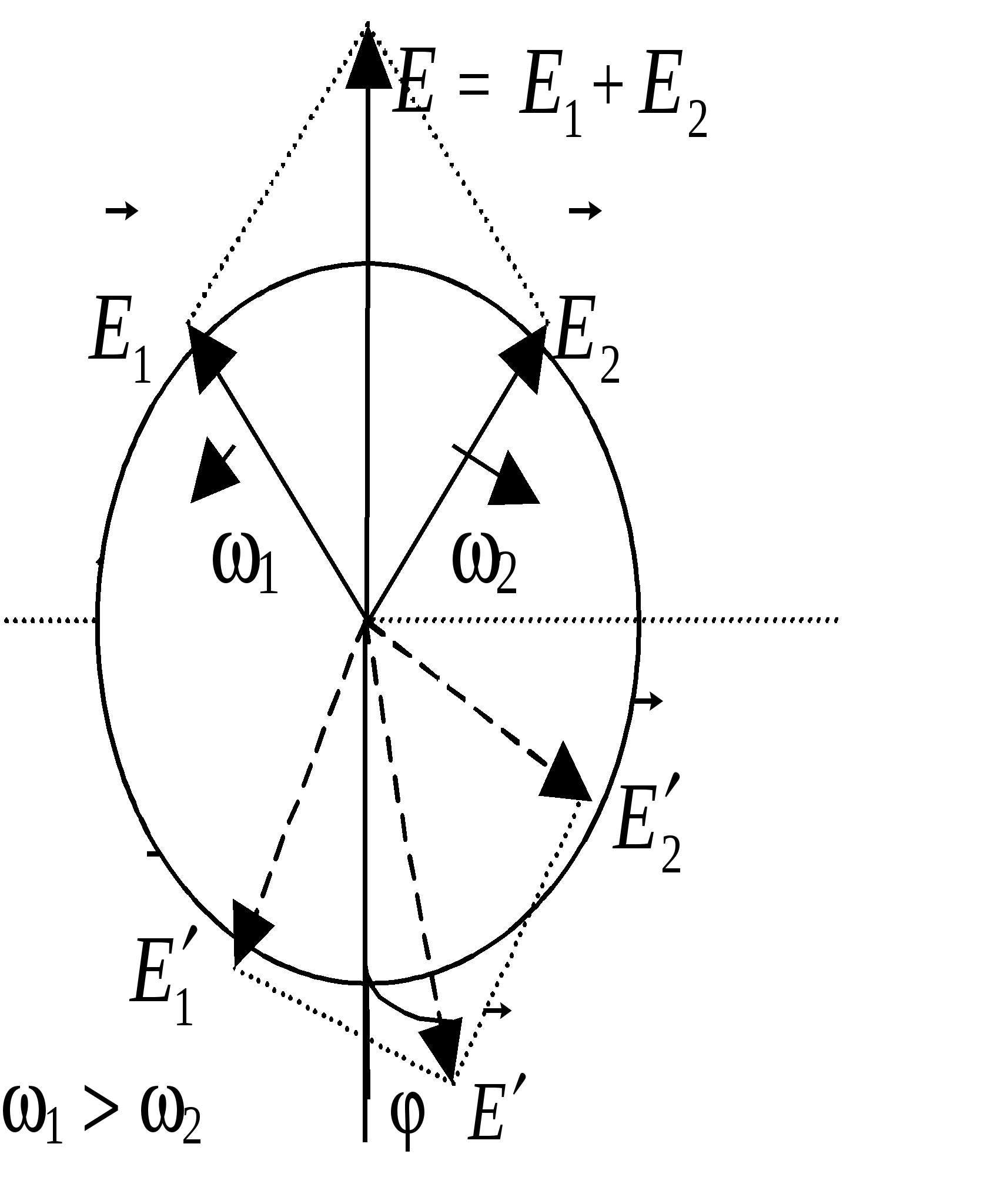








ренель объяснил явление вращения плоскости поляризации, разложив линейно поляризо­ванный свет на совокупность лево - и право циркулярно поляризованных волн (колебаний).
Он предположил также, что вещество в оптически активном состоянии обладает круговой асиммет­рией структурного, например внутримолекулярного характера, которая проявляет себя в различии показателей преломления n₁ и n₂ и угловых скоростей скоростей ₁ и ₂ распространения лево - и право поляризованных по кругу волн света. Одна из составляющих вектора вращается быстрее другой, и в результате с течением времени результирующее колебание поворачивается всё на больший угол относительно первона­чального направления.


5. Какие физические идеи и закономерности лежат в основе метода ис­следования» используемого в данной работе.

6. Дайте объяснение подученным в работе результатам и зависимостям.
Работа № 44 ИССЛЕДОВАНИЕ ХАРАКТЕРИСТИК ГАЗОВОГО ЛАЗЕРА

Каковы характерные отличия (и их причины) лазерного излучения от естественного света?

Если волна монохроматическая ("одноцветная"), то есть её частота пос­тоянна и начальная фаза  с течением времени не меняется, то вол­на называется когерентной.

Обычные источники света, в которых излучение света происходит за счёт хаотического теплового возбуждения отдельных атомов среды, излучают свет практически некогерентный. Однако, вырезая из результирующего светового потока уз­кий пучок света, излучаемый группой близких, синфазно излучающих ато­мов, можно получить волну, сохраняющую постоянной начальную фазу в течение времени  = 10^-8 - 10^-9 с. Это так называемое время когерентности естественного света - время непрерывного излучения света отдельным атомом

Свет с гораздо большей степенью когерентности создаётся в искус­ственных источниках света - лазерах. В них атомы активной среды излучают свет согласованно, синфазно, строго монохроматично, и начальная фаза световой волны способна длительно сохранять постоян­ным своё значение в данном месте с течением времени.

Какие физические идеи и закономерности лежат в основе принципа действия лазера?

В 1917 г. А. Эйнштейн предсказал возможность так называемого индуциро­ванного или
стимулированного, вынужденного излучения света атомами. Наря­ду со спонтанными (самопроизвольными) квантовыми переходами, атомы могут переходить в более низкие энергетические состояния индуцированно, под действием облучения светом. При этом они из­лучают свет с точно такими же характеристиками (частотой, фазой, поляризацией), как и вызвавший это излучение свет.

В 1940 г. В. А. Фабрикант указал на возможность использования явления вынужденного излучения для усиления и генерации когерентного света (электромагнитных волн).

В 1954 г. Н. Г. Басов и А. М. Прохоров, а также Ч. Таунс (США) создали первый генератор на основе вынужденного излучения с длиной волны  = 1,27 см. В 1960 г. в США был создан первый лазер - квантовый генератор света. Свет, излучаемый лазером, является строго монохроматическим, узконаправленным и когерентным.

Принцип действия лазера связан с созданием так называемой инверсной населённости энергетических уровней в системе атомов рабочего тела (активного вещества) лазера. В обычном, термодинамически равновесном состоянии, число атомов на энергетических уровнях (населенность уровней атомами) убывает экспоненциально с ростом энергии уровня. Но с помощью специального устройства накачки можно реализовать стационарное неравновесное состояние, при котором число атомов на каком-либо из возбужденных уровней будет большим их числа на каком-либо уровне с меньшей энергией.

При прохождении через активное вещество электромагнитной волны, частота  которой равна разности энергий Е состояний с инверсной населенностью, деленной на постоянную Планка h, волна будет не ослабляться, а усиливаться за счёт индуцированного излу­чения. Под её воздействием атомы активной среды согласованно переходят в низшие энергетические состояния, излучая волны, совпадающие по частоте, фазе и поляризации с соответствующими характеристиками падающей на вещество волны.

Двух уровней энергии для работы непрерывно действующего лазера не­достаточно. Устройство накачки одновременно и возбуждает, и сбрасывает атомы активной среды вниз. Выход был найден в использовании трёх "рабо­тающих" энергетических уровней.

Н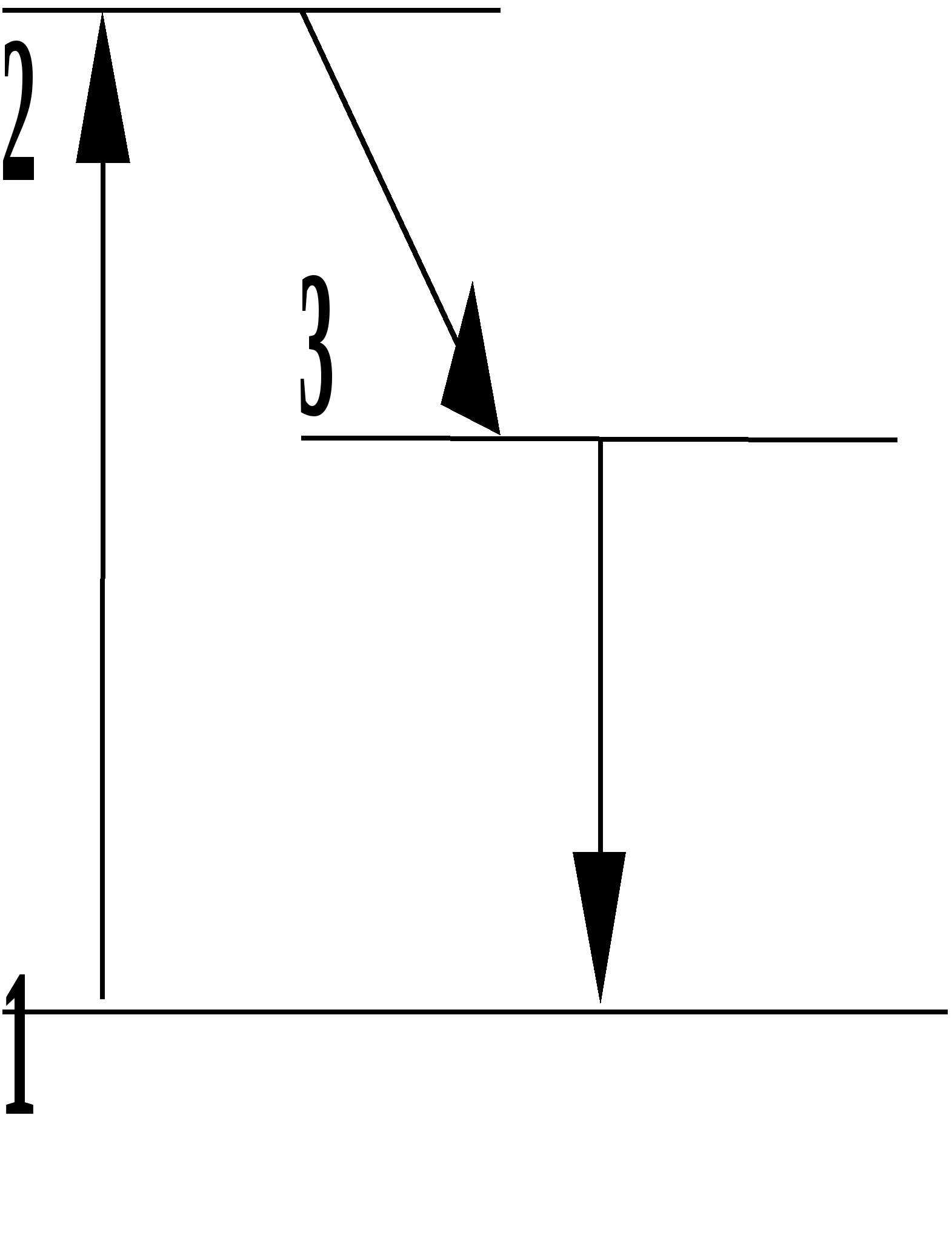


акачка (например, лампа-вспышка) переводит атомы из первого (нижнего) энергетического уровня на третий. Этот, возбужденный уровень, нестабилен, и за время порядка 10^-8 с атомы самопроизвольно переходят с него на более низкий - второй энергетический уровень. Он является метастабильным (так подбирается активное вещество, например - рубин), и на нём атомы "живут" примерно 10^-3 с, то есть в 10⁵ раз дольше, чем на верхнем уровне.

Переход же атомов из состояния 2 на нижний, исходный уровень осуществ­ляется под действием внешней электромагнитной волны и сопровождается вынужденным излучением, которое и представляет собой лазерное излучение.

В результате спонтанных, самопроизвольных переходов 2  1 излучаются волны (фо­тоны) всевозможных направлений. Те из них, которые идут под углом к оси кристалла, выходят из него, волны же, сонаправленные с осью кристалла, многократно отражаются от его посеребренных торцов и, непрерывно вызы­вая стимулированные переходы атомов активной среды, усиливаются. Один из торцов рубинового стержня делается полупрозрачным, а другой - зеркальным. Через полупрозрачный торец выходит мощный импульс (кратко­временный, порядка 10^-4 с) лазерного света.

Каковы основные необходимые элементы (и их функции), входящие в состав любого лазера?

Необходимыми частями любого квантового генератора являются рабочее тело (активная среда), устройство накачки и резонатор. Устройство накачки создает в системе атомов рабочего тела инверсную населенность атомов, при которой их число на одном из высших энергетических уровней оказывается большим, чем на каком либо из низших уровней. Резонатор представляет собой резонансную систему, настраиваемую на рабочую частоту (длину волны)  лазера, равную  = Е/h, где Е – разность энергий двух уровней атомов рабочего тела, между которыми осуществляется переход в лазере.

Один из первых генераторов когерентного света, работающих по трехуровневой схеме накачки с твердым телом в качестве активной среды, был создан в 1960 году Мейманом (США). Это был рубиновый (Al₂O₃ + 0,05 % Сr) лазер, активным веществом в котором являются ионы хрома Cr⁺³. Энергетическая схема уровней Cr⁺³ содержит две ближайшие к основному уровню C широкие энергетические полосы А и двойной метастабильный уровень В, переходы с которого на основной уровень С, соответствуют длинам волн 692,7 и 694,3 нм красного света (цвет рубина). Таким образом, в рубине для генерации и усиления света существенно наличие трех уровней, включая один метастабильный, то есть долгоживущий, обладающий повышенным временем жизни (с пониженной вероятностью спонтанных переходов).

П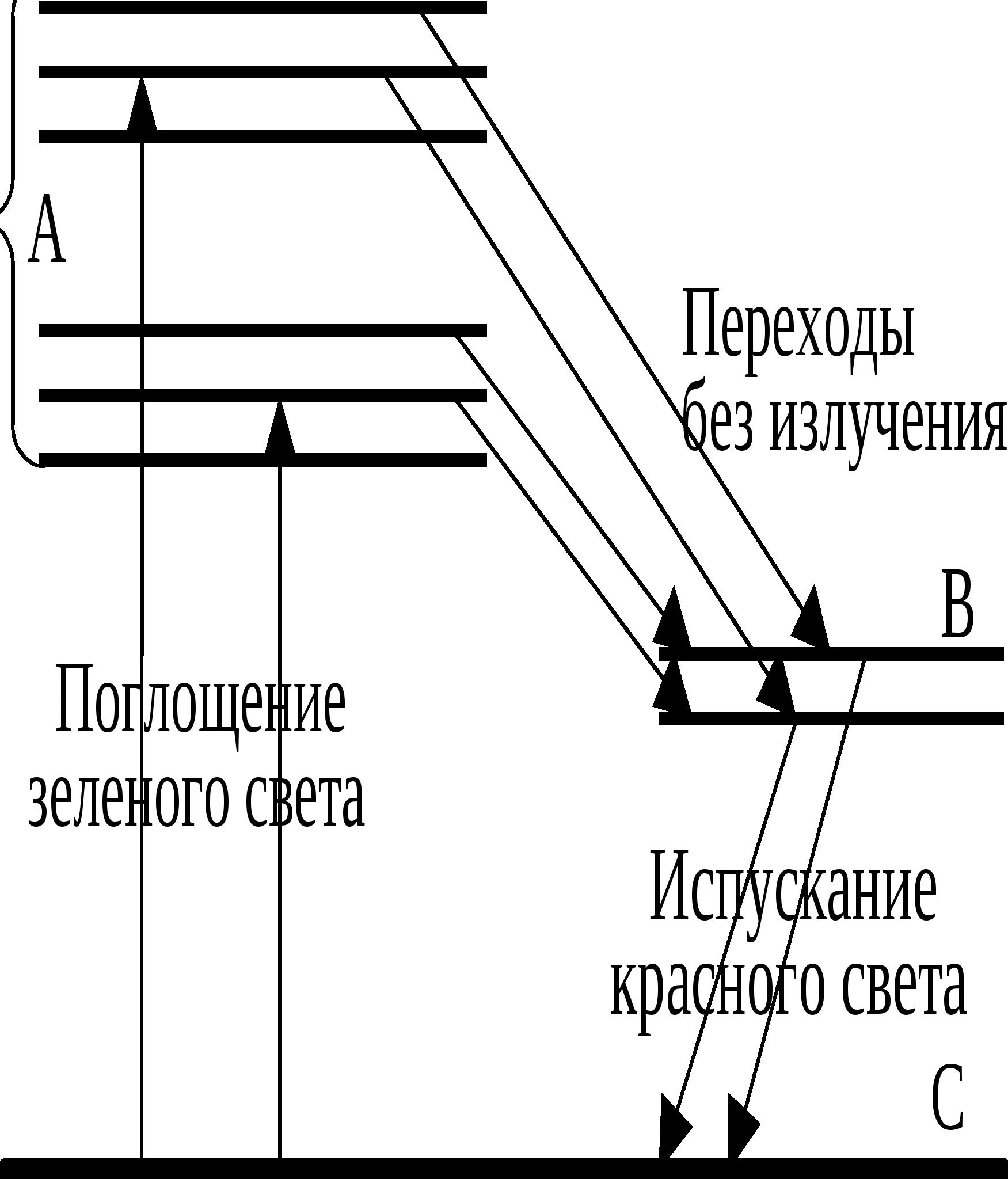


ри интенсивном облучении рубина зеленым светом мощной неон - криптоновой лампы наблюдается переход ионов хрома на уровни широкой полосы А, откуда наиболее вероятным является безызлучательный переход ионов на двойной уровень В с передачей избытка энергии кристаллической решетке рубина. Таким образом, можно создать условия, при которых населенность ионами двойного уровня В будет превышать заселенность основного уровня С, то есть уровни В и С будут заселены инверсно. Это и позволяет получить квантовый генератор света на линиях 692,7 и 694,3 нм.

Каковы принцип действия и устройство гелий – неонового лазера, используемого в работе?

В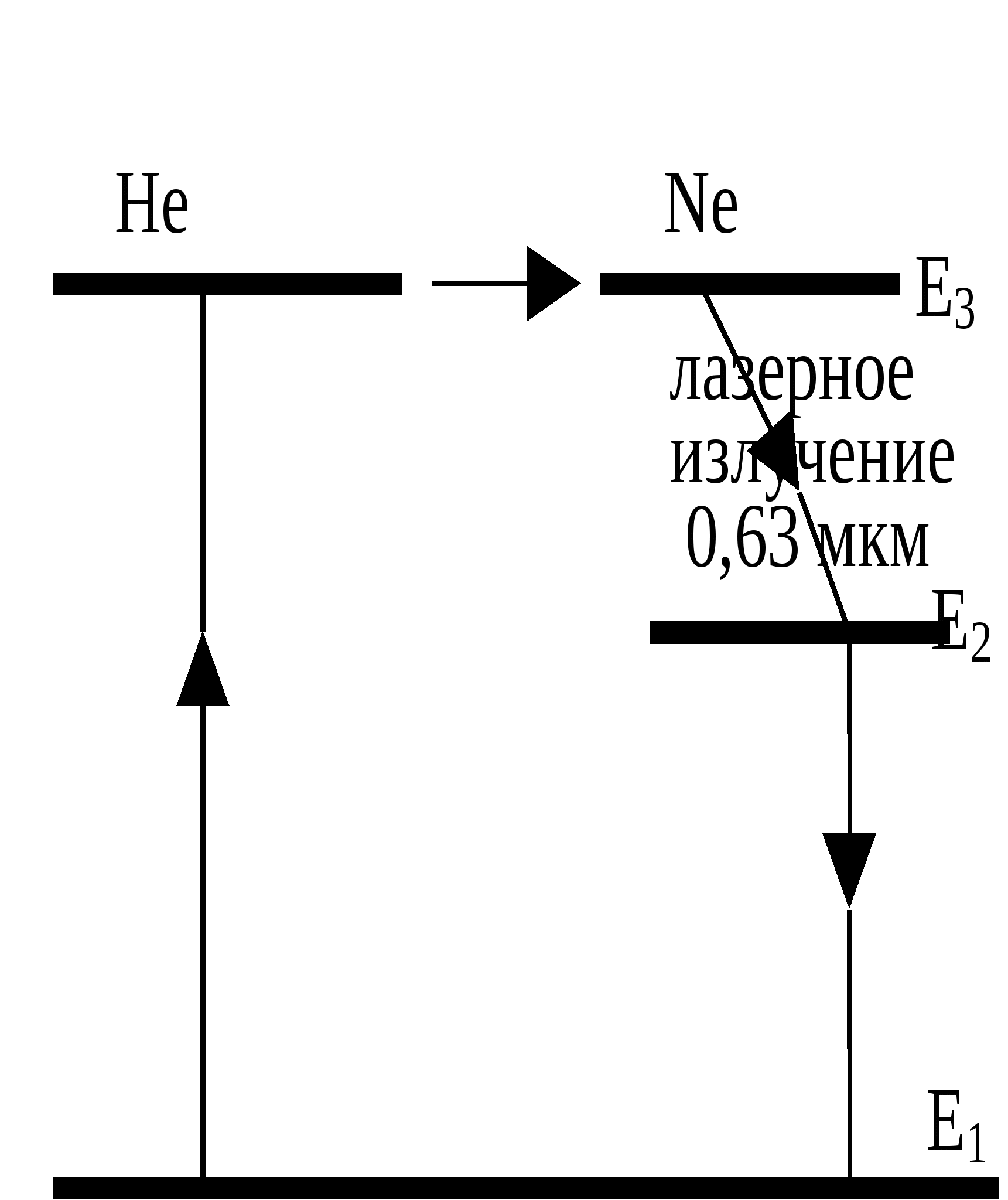


одном из газовых оптических квантовых генераторов света усиливающей (активной) средой служит плазма высокочастотного газового разряда, полученная в смеси гелия с неоном. Вследствие соударений с электронами в первую очередь возбуждаются (на уровень Е₃) более легкие атомы гелия. Затем возбужденные атомы гелия при столкновениях с атомами неона возбуждают их, то есть переводят на один из верхних энергетических уровней, близко расположенных к соответствующему уровню гелия. Переход атомов неона с этого метастабильного уровня на один из нижних уровней E₂ сопровождается излучением с длиной волны   0,63 мкм.

5. Проанализируйте полученные в работе результаты на их физическую достоверность и соответствие целям и задачам работы.
Работа №