Понятие экстремума функции. Локальный и глобальный экстремум. Точки экстремума функции
 Скачать 218.52 Kb. Скачать 218.52 Kb.
|
НЕОБХОДИМЫЕ И ДОСТАТОЧНЫЕ УСЛОВИЯ СУЩЕСТВОВАНИЯ ЭКСТРЕМУМОВТеорема Ферма (необходимый признак экстремума). Если функция 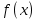 дифференцируема в точке дифференцируема в точке 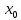 и имеет в этой точке экстремум, то её производная при и имеет в этой точке экстремум, то её производная при 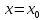 обращается в нуль, т.е. обращается в нуль, т.е. 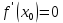 . .Теорема Ферма имеет простое геометрическое истолкование. Так как производная в точке 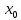 равна угловому коэффициенту касательной к графику функции в этой точке, то равенство равна угловому коэффициенту касательной к графику функции в этой точке, то равенство 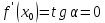 означает, что означает, что 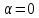 , т. е. касательная к кривой в этой точке параллельна оси Ox. , т. е. касательная к кривой в этой точке параллельна оси Ox.Следствие. Дифференцируемая функция может иметь экстремум лишь в тех точках, где производная равна нулю. Однако функция может иметь экстремум и в тех точках области определения, где производная не существует. 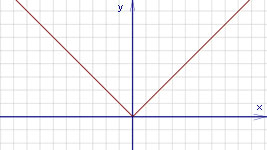 рис. 2 Пример 1. Функция 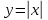 в точке в точке 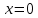 достигает минимума, но не дифференцируема при достигает минимума, но не дифференцируема при 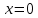 , так как в этой точке график не имеет определённой касательной (рис. 2).Курсовая работа курсовая работа курсовая работа курсовая работа , так как в этой точке график не имеет определённой касательной (рис. 2).Курсовая работа курсовая работа курсовая работа курсовая работа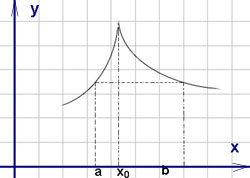 рис.3 Пример 2. Функция, изображённая на рисунке 3, имеет в точке 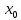 максимум, но не дифференцируема в этой точке, так как при максимум, но не дифференцируема в этой точке, так как при 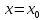 касательная к кривой образует с осью Ox угол касательная к кривой образует с осью Ox угол 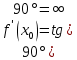 . .Замечание. Условия о том, что производная функции в точке равна нулю или не существует, являются необходимыми условиями экстремума, но не достаточными, поскольку можно привести примеры функций, для которых эти условия выполняются, но экстремума в соответствующей точке функция не имеет.2 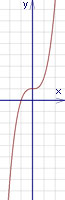 рис. 4 Пример 3. Функция 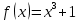 , изображённая на рисунке 4, имеет производную , изображённая на рисунке 4, имеет производную 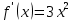 , которая обращается в нуль при , которая обращается в нуль при 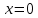 , однако в точке , однако в точке 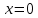 функция экстремума не имеет. функция экстремума не имеет.Те значения аргумента, при которых функция сохраняет непрерывность, а её производная обращается в нуль или не существует, называются критическими точками (или критическими значениями аргумента). Теорема Ферма является лишь необходимым признаком экстремума, так как не в каждой критической точке экстремум существует. Поэтому нужно располагать достаточными признаками, позволяющими судить, имеется ли в конкретной критической точке экстремум и какой именно - максимум или минимум.3 Первый достаточный признак экстремума. Если 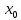 - критическая точка функции - критическая точка функции 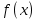 и в некоторой окрестности этой точки слева и справа от неё производная имеет противоположные знаки, то и в некоторой окрестности этой точки слева и справа от неё производная имеет противоположные знаки, то 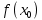 является экстремумом функции, причём: максимумом, если является экстремумом функции, причём: максимумом, если 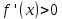 при при 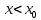 и и 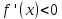 при при 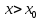 ; минимумом, если ; минимумом, если 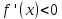 при при 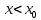 и и 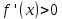 при при 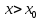 . .Если же вблизи точки 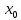 , слева и справа от неё, производная сохраняет знак, то это означает, что функция либо только убывает, либо только возрастает в некоторой окрестности точки , слева и справа от неё, производная сохраняет знак, то это означает, что функция либо только убывает, либо только возрастает в некоторой окрестности точки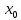 . В этом случае в точке . В этом случае в точке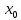 экстремума нет. экстремума нет.Таким образом, если 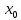 - критическая точка - критическая точка 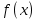 и при переходе через и при переходе через 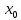 производная производная 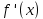 меняет знак, то меняет знак, то 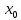 есть точка экстремума, причём точка максимума, если производная меняет знак с плюса на минус, и точка минимума, если с минуса на плюс. В противном случае в точке есть точка экстремума, причём точка максимума, если производная меняет знак с плюса на минус, и точка минимума, если с минуса на плюс. В противном случае в точке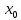 экстремума нет. экстремума нет.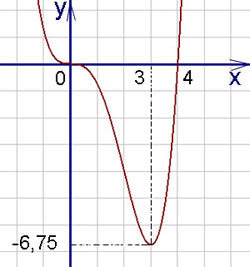 рис. 5 Пример 4. Исследовать на экстремум функцию 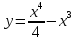 и построить её график. и построить её график.Решение. Функция определена и непрерывна на всей числовой прямой. Её производная 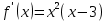 существует также на всей числовой прямой. Поэтому в данном случае критическими точками служат лишь те, в которых существует также на всей числовой прямой. Поэтому в данном случае критическими точками служат лишь те, в которых 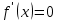 , т.е. , т.е. 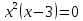 , откуда , откуда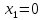 и и 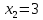 . Критические точки . Критические точки 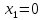 и и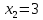 разбивают всю область определения функции на три интервала монотонности: разбивают всю область определения функции на три интервала монотонности: 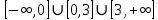 . Выберем в каждой из них по одной контрольной точке и найдём знак производной на этом промежутке. . Выберем в каждой из них по одной контрольной точке и найдём знак производной на этом промежутке.Для интервала 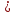 контрольной точкой может служить контрольной точкой может служить 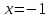 : находим : находим 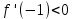 . Взяв в интервале . Взяв в интервале 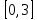 точку точку 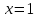 , получим , получим 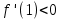 , а взяв в интервале , а взяв в интервале 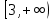 точку точку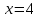 , имеем , имеем 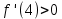 . Итак, в интервалах . Итак, в интервалах 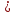 и и 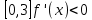 , а в интервале , а в интервале 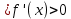 . Согласно первому достаточному признаку экстремума, в точке . Согласно первому достаточному признаку экстремума, в точке 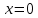 экстремума нет (так как производная сохраняет знак в интервале экстремума нет (так как производная сохраняет знак в интервале 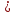 , а в точке , а в точке 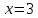 функция имеет минимум (поскольку производная при переходе через эту точку меняет знак с минуса на плюс). Найдём соответствующие значения функции: функция имеет минимум (поскольку производная при переходе через эту точку меняет знак с минуса на плюс). Найдём соответствующие значения функции: 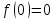 , а , а 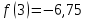 . В интервале . В интервале  функция убывает, так как в этом интервале функция убывает, так как в этом интервале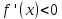 , а в интервале , а в интервале 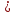 возрастает, так как в этом интервале возрастает, так как в этом интервале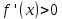 . .Чтобы уточнить построение графика, найдём точки пересечения его с осями координат. При 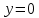 получим уравнение получим уравнение 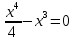 , корни которого , корни которого 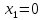 и и 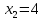 , т. е. найдены две точки , т. е. найдены две точки 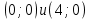 графика функции. Используя все полученные сведения, строим график (см. рис. 5). графика функции. Используя все полученные сведения, строим график (см. рис. 5).Второй достаточный признак экстремума. Если функция 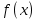 дважды дифференцируема и в точке дважды дифференцируема и в точке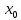 выполняются условия выполняются условия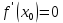 и и 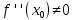 , то в этой точке функция имеет экстремум, причём максимум, если , то в этой точке функция имеет экстремум, причём максимум, если 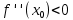 , и минимум, если , и минимум, если 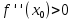 . .Замечание 1. Если в точке 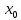 образуются в нуль обе производные, то в этой точке нельзя судить о наличии экстремума на основании второго достаточного признака. В этом случае нужно воспользоваться первым достаточным признаком экстремума. образуются в нуль обе производные, то в этой точке нельзя судить о наличии экстремума на основании второго достаточного признака. В этом случае нужно воспользоваться первым достаточным признаком экстремума.Замечание 2. Второй достаточный признак экстремума неприменим и тогда, когда в критической точке первая производная не существует (тогда не существует и вторая производная). В этом случае также нужно воспользоваться первым достаточным признаком экстремума. Пример 5. Исследовать на экстремум функцию 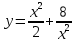 и построить её график. и построить её график.Областью определения функции является вся числовая прямая, кроме точки 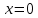 , т.е. , т.е. 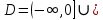 . .Для сокращения исследования можно воспользоваться тем, что данная функция чётная, так как 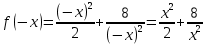 . Поэтому её график симметричен относительно оси Oy и исследование можно выполнить только для интервала . Поэтому её график симметричен относительно оси Oy и исследование можно выполнить только для интервала 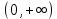 . .Находим производную 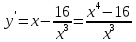 и критические точки функции: и критические точки функции:1) 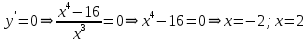 2) 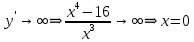 но функция терпит разрыв в этой точке, поэтому она не может быть точкой экстремума. Таким образом, заданная функция имеет две критические точки: 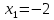 и и 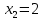 . Учитывая чётность функции, проверим по второму достаточному признаку экстремума только точку . Учитывая чётность функции, проверим по второму достаточному признаку экстремума только точку 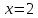 . Для этого найдём вторую производную . Для этого найдём вторую производную 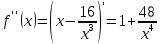 и определим её знак при и определим её знак при 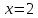 : получим : получим 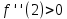 . Так как . Так как 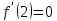 и и 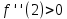 , то , то 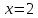 является точкой минимума функции, при этом является точкой минимума функции, при этом 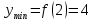 . .Чтобы составить более полное представление о графике функции, выясним её поведение на границах области определения: 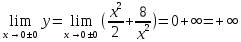 (здесь символом  обозначено стремление обозначено стремление  к нулю справа, причём к нулю справа, причём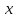 остаётся положительным; аналогично остаётся положительным; аналогично 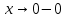 означает стремление x к нулю слева, причём x остаётся отрицательным). Таким образом, если означает стремление x к нулю слева, причём x остаётся отрицательным). Таким образом, если 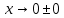 , то , то 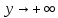 . Далее, находим . Далее, находим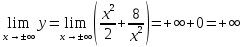 , ,т.е. если 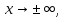 то то 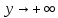 .4 .4Точек пересечения с осями график функции не имеет. 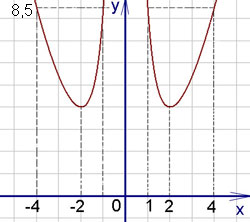 рис. 6 |
