Понятие экстремума функции. Локальный и глобальный экстремум. Точки экстремума функции
 Скачать 218.52 Kb. Скачать 218.52 Kb.
|
4. ЭКСТРЕМАЛЬНЫЕ ЗАДАЧИ В АЛГЕБРЕ И ГЕОМЕТРИИСреди задач математики, с помощью которых решают проблемы оптимизации, следует выделить задачи на экстремумы и оптимумы. Эти задачи в курсе математики старшей школы встречаются чаще всего, именно они, в свою очередь, являются фундаментом рассмотрения оптимизационных задач вообще. Из математического анализа известно, что если числовая функция 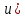 непрерывна, то экстремум непрерывна, то экстремум 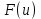 на на 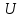 может достигаться лишь в тех точках может достигаться лишь в тех точках 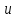 , в которых , в которых 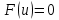 или или 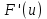 не существует или является граничной и для множества не существует или является граничной и для множества 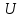 . .Описанным способом поиска экстремума можно пользоваться, начиная с 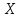 класса во всех тех случаях, когда решение задач сводится к исследованию функции, которая вместе с её производной имеет достаточно простой вид. В большинстве практических задач зачастую вычисление производной представляет большие трудности и нередко даже неизвестно, существует ли производная в интересующих нас точках. Бывает так, что функция класса во всех тех случаях, когда решение задач сводится к исследованию функции, которая вместе с её производной имеет достаточно простой вид. В большинстве практических задач зачастую вычисление производной представляет большие трудности и нередко даже неизвестно, существует ли производная в интересующих нас точках. Бывает так, что функция 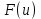 задана лишь таблично или вообще трудно представить задачу в аналитическом виде. В тех случаях, когда производная всё же вычислена, решение уравнения задана лишь таблично или вообще трудно представить задачу в аналитическом виде. В тех случаях, когда производная всё же вычислена, решение уравнения 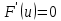 может также привести к серьёзным трудностям. может также привести к серьёзным трудностям.Важно иметь методические приёмы, способы решения экстремальных задач, не требующих вычисления производной. Это происходит, например, при решении задач на дискретную оптимизацию. Особым типом экстремальных задач являются задачи линейного программирования, которые решаются без помощи производной. Неприменима производная и при решении многих геометрических задач. Введение экстремальных задач в обучение педагогически оправдано, так как они с достаточной полнотой закладывают в сознание учащихся понимание того, как человек ищет, постоянно добивается решения жизненных задач, чтобы получающиеся результаты его деятельности были как можно лучшими. Решая задачи указанного типа, учащиеся видят, с одной стороны, абстрактный характер математических понятий, с другой – большую и эффективную их применимость к решению практических, жизненных задач. Такая постановка экстремальных задач способствует расширению сферы приложений учебного материала, повышает роль этих задач в осуществлении глубокой цели математического образования школьников – обучать приложению математики в различных областях человеческой деятельности. Экстремальные задачи могут помочь школьнику ознакомиться с некоторыми идеями и прикладными методами школьного курса математики, которые часто применяются в трудовой деятельности, в познании окружающей действительности. Такие задачи могут серьёзно повлиять на содержание учебного материала, на аспекты применения приложений изучаемой теории на практике. В школе на уроках математики учитель, как правило, ставит более скромную цель: воспитывать учащихся на примерах содержательных экстремальных задач, формировать у них научное мировоззрение, глубокие взгляды на процессы, происходящие как в природе, так и в общественной жизни, показывать важность математических знаний и умений решать задачи. Решение экстремальных задач способствует углублению и обогащению математических знаний учащихся. Через задачи они знакомятся с экстремальными свойствами изучаемых функций, рассматриваемых на непрерывном или дискретном множествах, с некоторыми свойствами неравенств. Изучая свойства той или иной геометрической фигуры, учащиеся с помощью задач приобретают знания об экстремальных свойствах этой фигуры, а также учатся применять их к решению прикладных задач. Следует отметить особую значимость постановки экстремальных задач в школьном курсе математики в воспитании исследовательской культуры учащихся. Ведь все решения таких задач предлагаются на уровне исследования математической модели и на уровне исследования реальной ситуации с использованием оптимизационных средств. Кроме того, в процессе решения большей части экстремальных задач широко и удачно используются эвристические приёмы, которые в отличие от алгоритмических могут подсказать путь решения предлагаемых задач. Для решения экстремальных задач существуют следующие методы: 1. Метод опорной функции; 2. Метод оценки; 3. Метод перебора; 4. Метод преобразования плоскости. Рассмотрим некоторые из перечисленных методов на конкретных примерах. Пример 7. Масса чугунной болванки 16кг. Сколько болванок потребуется, чтобы отлить 41 деталь массой 12 кг каждая? Решение. Первый способ. Поскольку масса одной детали 12 кг, то 41 деталь будет весить: 12*41 = 492 кг. Далее рассуждаем так: одна болванка весит 16 кг, поэтому потребуется 31 болванка (492 : 16 = 30 (12 – остаток)). Не обращая внимания на остаток, ученики делают ошибочный вывод. Вместо того, чтобы написать «31 болванка», пишут «30 болванок». Второй способ. Пусть n — количество болванок, тогда 16n – масса болванок, 12*41 – масса деталей. Далее ученикам предстоит сравнить и оценить значение выражений, чтобы поставить соответствующий знак между ними: 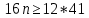 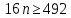 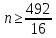 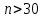 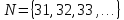 Наименьшее число болванок равняется 31. Если ознакомить учеников с условием задачи и при этом не задавать наводящих вопросов, то на поставленный в задаче вопрос некоторые ученики дают такой ответ: на 41 деталь нужно использовать 41 болванку, т. е. из каждой болванки изготавливают одну деталь. Чтобы исправить ошибку ученика, нужно заставить его тщательно прочитать задачу, обратить внимание на слова «отлить 41 деталь». Подобные ситуации, в которые попадают ученики при решении задач, дают учителю возможности для воспитательной работы. Он формирует у учащихся сознательное отношение к профессии, показывает, что высокий математический уровень знаний становится нужным и полезным в трудовой деятельности. Поскольку встречаются задачи с двойным неравенством, то можно решать задачи на нахождение наибольшего и наименьшего значения линейного выражения ах + в, где x – переменная, m и n – целые неотрицательные числа. При нахождении наименьшего и наибольшего значения выражения ах + в, ученики должны уметь: 1) решать двойное неравенство; 2) находить то значение переменной, которое удовлетворяет требованию задачи; 3) оценивать значение выражения. При решении приходится обращаться к таким вопросам: а) Как изменяется сумма при изменении слагаемого? б) Как изменяется разность при изменении вычитаемого и уменьшаемого? в) Как изменяется произведение при изменении сомножителей? Пример 8. Стоимость телеграммы вычисляется почтовыми работниками по следующему правилу: по 5 рублей за каждое слово и ещё 20 рублей за отправку телеграммы. Какая может быть наибольшая и наименьшая цена телеграммы, если количество слов в телеграмме определяется решением неравенства 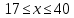 ? ? Решение задачи сводится к нахождению наибольшего и наименьшего значения выражения 5х + 20, если 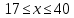 и хN. Сначала можно предложить вычислить значение выражения при нескольких значениях переменной, взятых из промежутка и хN. Сначала можно предложить вычислить значение выражения при нескольких значениях переменной, взятых из промежутка 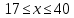 . Заметим, что сумма будет наибольшая, если слагаемое . Заметим, что сумма будет наибольшая, если слагаемое 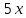 будет наибольшим, т. е. будет равно 5·40, и наименьшая, если слагаемое будет наибольшим, т. е. будет равно 5·40, и наименьшая, если слагаемое 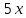 будет наименьшим, т. е. будет равно 5*17. Заметим, что второе слагаемое постоянно. будет наименьшим, т. е. будет равно 5*17. Заметим, что второе слагаемое постоянно. Среди экстремальных задач геометрические задачи на вычисление площадей и периметров представляют большой интерес. Решение этих задач методом оценки формирует первое представление о максимальном произведении при постоянной сумме двух переменных и о минимальной сумме при постоянном произведении. Рассмотрим примеры таких задач. Пример 9. Начертите прямоугольник, периметр которого 36 см, вычислите его площадь. Решение этой задачи можно оформить в виде такой таблицы:
Отсюда вывод: наибольшая площадь S = 81 при а = в = 9 см. Построение прямоугольников и запись решения в виде таблицы помогает лучше видеть, как изменяется площадь прямоугольника с постоянным периметром и как изменяется периметр прямоугольника с постоянной площадью. Остановимся на решении экстремальных задач в разделе «Натуральные числа». Здесь на первом этапе решаются самые простые задачи, где число рассматриваемых элементов невелико. Это во многом упрощает организацию работы, требует меньше времени и создаёт хорошую возможность детям увидеть особенности применения метода перебора к решению задач. Пример 10. С помощью цифр 5, 2 и 7 напишите все трёхзначные числа, в каждом из которых все цифры различны. Среди найденных чисел найдите наибольшее и наименьшее число. Очень часто мы встречаемся с такими фактами. Ученики решили задачу, т. е. нашли числа 527, 572, 275, 257, 752, 725 и указали наибольшее и наименьшее число. Но мала эффективность таких методических приёмов, если ученики не проявили творческого мышления, не увидели никакой новизны, не нашли самостоятельно приёмов составления перестановок, т. е. не нашли алгоритма построения перестановок, не подметили упорядочения чисел, не сделали вывод о том, в каком порядке расположены цифры в наибольшем и наименьшем числе. На первый взгляд, кажется, что это очень простая задача, но она несёт большую теоретическую нагрузку. Ученик знакомится с упорядоченными множествами, с методом перебора, перестановками, с методическими приёмами поиска экстремальной перестановки. Пример 11. В кабинет математики к началу консультации пришли 3 ученика (А, В, С). Предварительный разговор позволил учителю выяснить, что для рассмотрения вопроса ученика А требуется 5 мин, ученика В – 2 мин, ученика С – 7 мин. после получения ответа на свой вопрос ученик уходит. Как организовать консультацию, чтобы каждый из учеников находился в кабинете как можно меньше времени? Иными словами, учитель хочет как можно меньше задержать каждого из них, т. е. минимизировать общее время, проведённое учениками в кабинете. Для лучшего понимания задачи можно предложить ученикам записать условие задачи в виде таблицы:
Это даст возможность не только облегчить решение задачи, но и будет содействовать формированию понятия о матрице (хотя о таком понятии ничего не говорим). Решение этой задачи можно проиллюстрировать такой таблицей:
Оптимальный вариант:
Суммарное время: 3 + 8 + 15 = 26 мин. Итак, этот приём решения имеет много общего с решением предыдущей задачи, которая была как бы подготовительной, с её помощью ученикам легче было найти приём решения данной задачи. Последняя задача дала много интересного и полезного. Здесь появилась возможность подвести учащихся к пониманию способов построения искомых последовательностей (3, 5, 7) и (3, 8, 5). Ученикам не даются указания, как записывать рекуррентные формулы для нахождения экстремальных перестановок, последовательностей. С этим понятием знакомят учеников в 9 классе. Решение задач на экстремальные перестановки способствует приобретению учениками определённых комбинаторных навыков и знаний, более глубокому пониманию изучаемого материала. Нахождение наибольших и наименьших значений величин методом перебора рассматривается частично при изучении тем: «Наибольший общий делитель» и «Наименьшее общее кратное». Понятие экстремума в этих темах связывается с понятием наивыгоднейших значений величин. Решение экстремальных задач в курсе алгебры проходит в два этапа. На первом этапе рассматривается неопределенная задача, текст которой переводится на математический язык в виде неопределённого уравнения (функции), которое допускает много или бесконечно много решений. На втором этапе по тем или иным признакам, которые заданы в явном или неявном виде, определяется, какое из решений задачи наиболее выгодно. Темы курса алгебры, в которых приходится решать экстремальные задачи и формировать методы их решения, рассматриваем следующим образом: 1) Линейная функция. 2) Системы линейных уравнений. 3) Рациональные дроби. 4) Неравенства. 5) Квадратичная функция. 6) Последовательности. Арифметическая прогрессия. 7) Преобразование выражений, содержащих квадратные корни.6 Ознакомимся с решением экстремальных задач по теме «Линейная функция». Решение задач данной темы сводится к нахождению экстремума линейной функции 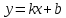 , где , где 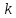 и и 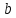 – постоянные. Если эту функцию рассматривать на отрезке, то она будет иметь на нём наибольшее и наименьшее значение. При – постоянные. Если эту функцию рассматривать на отрезке, то она будет иметь на нём наибольшее и наименьшее значение. При 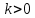 наименьшее значение у принимает в точке наименьшее значение у принимает в точке 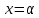 , а наибольшее – в точке , а наибольшее – в точке 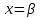 , при , при 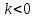 функция функция 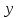 в точке в точке 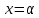 принимает наибольшее значение, а в точке принимает наибольшее значение, а в точке 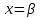 — наименьшее. — наименьшее.Рассмотрим одну из задач, решение которой сводится к нахождению наибольшего и наименьшего значения линейной функции одной переменной на некотором отрезке и покажем применение линейной функции в практике. Задача 12. На совхозной ферме нужно провести водопровод длиной 167м. Имеются трубы длиной 5 м и 7 м. Сколько нужно использовать тех и других труб, чтобы сделать наименьшее количество соединений (трубы не разрезать)? Учитывая, что количество как одних, так и других труб может изменяться, ученики предлагают количество 7-метровых труб обозначить через х, а 5-метровых – через у. Тогда 7х – длина 7-метровых труб, 5у – длина 5-метровых труб. Отсюда получаем неопределённое уравнение 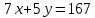 . Выразив, например, переменную у через переменную х, получим: . Выразив, например, переменную у через переменную х, получим: 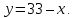 Так как х, у N, то методом перебора легко найти соответствующие пары значений х и у, которые удовлетворяют уравнению 7х + 5у = 167. К ним относятся пары (1; 32), (6; 25), (11; 18), (16; 11), (21; 4). Из этих решений наиболее выгодное последнее, т. е. х = 21, у = 4. Рассмотрим более сложные экстремальные задачи, в которых нахождение наибольшего или наименьшего значения сводится к решению неравенства вида 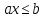 , где , где 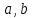 – заданные числа и хN. Понятия «наибольшее», «наименьшее» значение в этих задачах больше всего связаны с понятием «наивыгоднейших» значений величин. – заданные числа и хN. Понятия «наибольшее», «наименьшее» значение в этих задачах больше всего связаны с понятием «наивыгоднейших» значений величин.Задача 13. Предположим, что населенные пункты С, расположенные на отрезке АВ, снабжаются некоторым потребительским товаром как из пункта А, так и из пункта В. Одна тонна этого товара в А обходится в 5 тыс. руб., а в В – в 7 тыс. руб. Транспортировка 1 т груза на расстояние 1 км стоит 200 руб. расстояние между пунктами А и В равно 100 км. Нужно составить план снабжения товарами пунктов С, при котором будет допускаться минимальный расход денег. Попробуем представить эту жизненную ситуацию в математическом описании. Пусть расстояние АС = х, тогда ВС = 100 – х. Стоимость транспортировки 1т груза из пункта А в пункт С равна (5 + 0,2х) тыс. руб. Стоимость транспортировки 1 т груза из пункта В в пункт С равна: 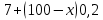 тыс. руб, или тыс. руб, или 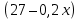 тыс. руб. Узнаем, на каком расстоянии стоимость транспортировки груза от пункта А будет не больше, чем от пункта В, т. е. тыс. руб. Узнаем, на каком расстоянии стоимость транспортировки груза от пункта А будет не больше, чем от пункта В, т. е.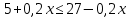 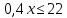 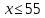 Итак, из пункта А нужно транспортировать товар на расстояние не больше, чем на 55 км, а из В – не больше, чем на 45 км. Целесообразно предложить ученикам подсчитать, сколько будет стоить транспортировка 1 т груза в пункт С, который находится от А на расстоянии 20 км, 55 км, 70 км, а потом от В – на расстоянии 80 км, 45 км, 30 км. Наконец, необходимо сделать вывод и оценить важность применяемых математических методов. При решении таких задач есть возможность сделать так, чтобы каждый из учеников почувствовал себя в роли экономиста, в роли директора, бригадира, заместителя, рабочего. Достаточно много экстремальных задач можно решать при изучении темы «Квадратный трехчлен». К исследованию квадратичной функции на экстремум сводятся многие прикладные задачи не только алгебры, но и экономики, геометрии, физики, техники. Простейшим и в то же время универсальным способом для решения экстремальных задач, связанных с квадратичной функцией, является способ выделения квадрата двучлена.7 Примером могут быть следующие задачи. Задача 14. Для строительства склада заготовлен материал на наружные стены длиной 32 м и высотой 4 м. Какими должны быть размеры (в виде прямоугольного параллелепипеда), чтобы склад имел наибольший объём? Решение задачи сводится к исследованию функции: 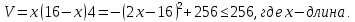 Задача 15. Сопротивление f дороги движению автомобиля при скорости v выражается следующими формулами: а) на хорошем шоссе: 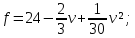 б) на плохом шоссе: 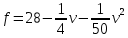 в) на булыжной мостовой: 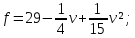 г) на мягкой грунтовой дороге: 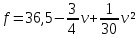 . .При какой скорости сопротивление должно быть наименьшим? Задача 16. Тело брошено вертикально вверх с высоты 25 м с начальной скоростью 4 м/с. Считая ускорение земного притяжения равным 10 м/с² и пренебрегая сопротивлением воздуха, найдите, на какую максимальную высоту взлетит тело? Как видно из приведенных примеров, решение экстремальных задач даёт возможность установить более тесную межпредметную связь алгебры, геометрии и физики. При их решении ученики приобретают не только математическую информацию, но и знания из курса физики. Решение физических задач поучительно с точки зрения математики, так как можно показать тонкости тех или иных математических приемов в действии, в их практическом приложении. В частности эти задачи помогают осознать, что функция, заданная аналитической формулой, может выражать зависимость между реальными величинами в самых различных явлениях и процессах.8 Метод опорных функций часто используется и при решении задач на геометрические экстремумы, если условие задачи удается формализовать, т.е. свести её к исследованию формулы. Характерной особенностью геометрических задач на нахождение экстремумов, решаемых методом опорных функций, является составление геометрических формул, непосредственно подсказанных соответствующими теоремами. Речь идет о таких теоремах и формулах, как теоремы косинусов, синусов; формулы для вычисления площадей; формулы метрических соотношений в прямоугольном треугольнике и других. Решение геометрических задач на нахождение наибольшего и наименьшего значения геометрической величины чаще всего сводится к исследованию опорных функций вида 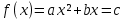 . . Но иногда решение таких задач с помощью опорной функции сводится непосредственно к использованию не одной известной геометрической формулы, а нескольких вспомогательных теорем (формул), которые в свою очередь могут потребовать новых теорем. Такое использование системы теорем (формул) требует и соответствующих логических рассуждений. Примером может быть следующая задача.9 Задача 17. На земельном участке, имеющем форму остроугольного треугольника АВС, надо построить дом прямоугольной формы так, чтобы он прилегал к сторонам участка. Известно, что АС = 40 м, h = ВД = 20 м. Какую наибольшую площадь участка может занять проектируемое здание? Пусть MN = х, МК = у. Так как 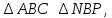 то то 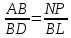 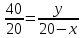 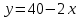 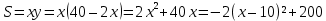 . .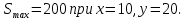 Итак, решение задачи сводится к исследованию опорной функции вида 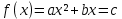 . .Решение: найдем полупериметр прямоугольника: 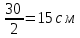 . Обозначим через . Обозначим через 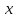 длину стороны прямоугольника (любую). Тогда длину стороны прямоугольника (любую). Тогда 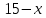 – длина смежной стороны: – длина смежной стороны: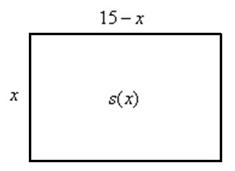 рис. 7 Составим функцию площади прямоугольника: 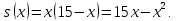 Найдем критические точки: 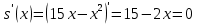 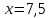 критическая точка. критическая точка.Проверим выполнение достаточного условия экстремума. 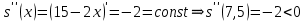 , значит, функция , значит, функция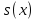 достигает максимума в точке достигает максимума в точке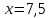 . .Таким образом 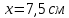 – оптимальная длина стороны прямоугольника, длина смежной стороны: – оптимальная длина стороны прямоугольника, длина смежной стороны: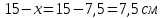 ; при этом максимальная площадь: ; при этом максимальная площадь: 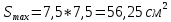 Ответ: оптимальный прямоугольник представляет собой квадрат со стороной 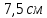 ; при этом максимальная площадь: ; при этом максимальная площадь: 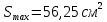 . .Задача 18. Найти прямоугольник наибольшего периметра, который можно вписать в полукруг данного радиуса Решение: выполним чертёж: 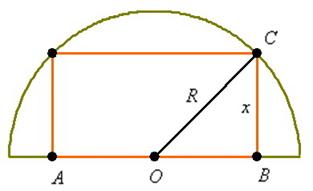 рис. 8 Пусть 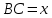 (как вариант, за «икс» можно обозначить (как вариант, за «икс» можно обозначить 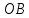 или даже или даже 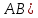 . Рассмотрим прямоугольный . Рассмотрим прямоугольный 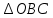 . По теореме Пифагора: . По теореме Пифагора: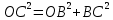 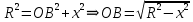 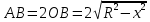 Составим функцию периметра прямоугольника: 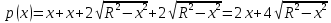 Найдём критические точки: 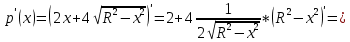  =0 =0Решим простейшее иррациональное уравнение: 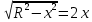 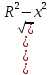 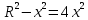 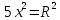 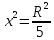 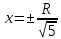 Уравнению 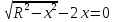 удовлетворяет корень удовлетворяет корень 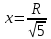 (корень (корень 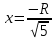 появился в результате возведения обеих частей в квадрат и является посторонним). появился в результате возведения обеих частей в квадрат и является посторонним).Проверим выполнение достаточного условия экстремума. Способ первый: определим знаки производной: 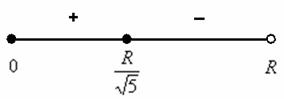 Примечание: используем стандартный метод интервалов: в производную 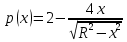 подставляем какое-нибудь значение, лежащее левее точки подставляем какое-нибудь значение, лежащее левее точки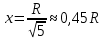 , например, , например, 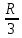 и подставляем какое-нибудь значение из правого интервала – проще всего взять и подставляем какое-нибудь значение из правого интервала – проще всего взять 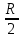 . .Вывод: функция 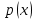 достигает максимума в точке достигает максимума в точке 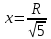 . .Способ второй: 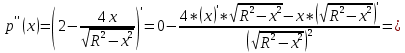 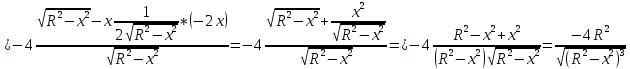 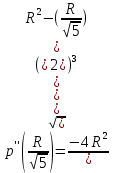 , значит, функция , значит, функция 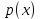 достигает максимума в точке достигает максимума в точке 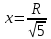 . .Таким образом, размеры оптимального прямоугольника: 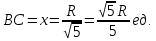 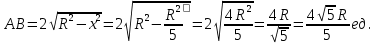 При этом максимальный периметр: При этом максимальный периметр: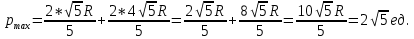 Ответ: оптимальный прямоугольник имеет размеры Ответ: оптимальный прямоугольник имеет размеры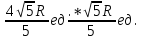 , при этом максимальный периметр: , при этом максимальный периметр: 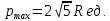 Задача 19. Найти оптимальные размеры банки, которую можно вырезать из данного листа прямоугольной формы с наименьшими отходами. Решение: составим функцию площади полной поверхности цилиндра 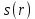 , зависящую от его радиуса. Пусть , зависящую от его радиуса. Пусть 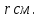 – радиус дна (и крышки) консервной банки: – радиус дна (и крышки) консервной банки: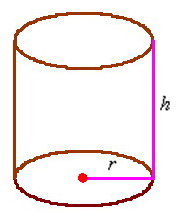 рис. 9 Тогда площадь дна: 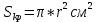 . Столько же и площадь крышки. . Столько же и площадь крышки.По условию объём консервной банки равен 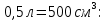 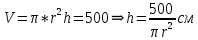 Выразим через площадь боковой поверхности банки: 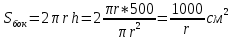 Площадь полной поверхности банки равна сумме площадей дна, крышки и боковой поверхности: 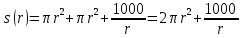 Найдём критические точки: 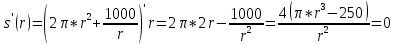 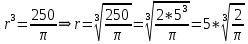 – критическая точка. – критическая точка.Проверим выполнение достаточного условия экстремума: 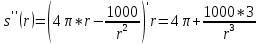 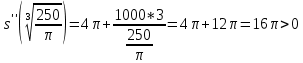 , значит, функция , значит, функция 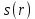 достигает минимума в точке достигает минимума в точке 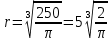 . .Высота оптимальной банки: 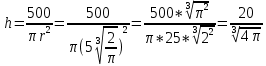 Ответ: радиус основания оптимальной банки: 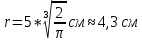 , её высота: , её высота: 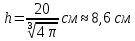 Задача 20. Из листа картона прямоугольной формы необходимо вырезать коробку наибольшей вместимости. Найти размеры коробки. Решение: пусть 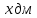 – сторона вырезаемых по углам квадратов (высота будущей коробки). Тогда смежные стороны дна коробки составят – сторона вырезаемых по углам квадратов (высота будущей коробки). Тогда смежные стороны дна коробки составят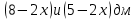 : :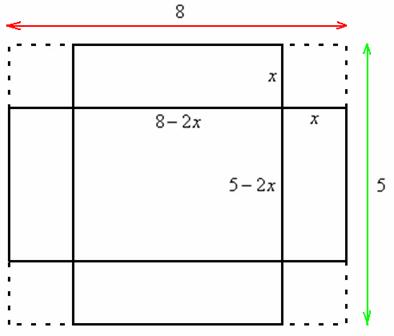 рис. 10 Составим функцию объёма коробки: 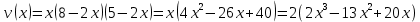 Найдём критические точки: 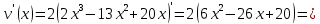 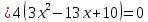 Решим квадратное уравнение: 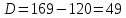 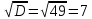 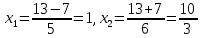 – критические точки. – критические точки. Второе значение не удовлетворяет геометрическому смыслу задачи, поскольку суммарная длина отреза сверху и снизу 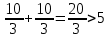 (ширины листа). (ширины листа). Проверим выполнение достаточного условия экстремума: 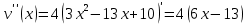 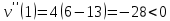 , значит, функция , значит, функция 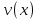 достигает максимума в точке достигает максимума в точке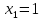 . .Ответ: размеры оптимальной коробки: 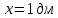 – высота (сторона вырезаемых по углам квадратов); – высота (сторона вырезаемых по углам квадратов);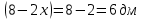 – длина; – длина;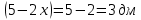 – ширина;при этом максимальный объем: – ширина;при этом максимальный объем: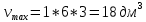 . .Геометрические задачи в силу своих особенностей и возможностей допускают различные методы решения. Так, в частности, одна и та же задача может быть решена как методом преобразования плоскости, так и алгебраическими методами. Во многих геометрических экстремальных задачах решение алгебраическими средствами становится очень сложным, а методом преобразования плоскости они решаются проще.10 Формирование умения решать задачи на экстремумы с помощью производной – одна из важных целей изучения начал математического анализа в средней школе. Задачи этого типа имеют чёткую прикладную направленность. Действительно, в них представлены все фазы построения и использования математической модели: формализация – составление функции, описывающей условия задачи; решение формализованной задачи – поиск значений аргумента, в которых значение производной функции равно нулю или в которых она не существует (критических точек); интерпретация – анализ критических точек с учётом особенностей задачи. Вместе с тем следует учитывать, что задачи, которые решаются с использованием производной, во многих случаях оказывается возможным решить и другими, элементарными методами. Сопоставление различных способов решения экстремальных задач, проведенное на нескольких примерах, может оказаться полезным в нескольких отношениях: - можно сравнить единообразный характер решения задач с помощью производной с приемами, которые приходится выискивать, если производной не пользоваться; - решение экстремальных задач элементарными методами обычно находится с большим трудом; оно включает элемент догадки и творчества. В то же время использование производной может оказаться принципиально не сложным, но связанным с достаточно большими вычислениями. |
