Понятие экстремума функции. Локальный и глобальный экстремум. Точки экстремума функции
 Скачать 218.52 Kb. Скачать 218.52 Kb.
|
ОГЛАВЛЕНИЕВВЕДЕНИЕ 3 1.ПОНЯТИЕ ЭКСТРЕМУМА ФУНКЦИИ. ЛОКАЛЬНЫЙ И ГЛОБАЛЬНЫЙ ЭКСТРЕМУМ. ТОЧКИ ЭКСТРЕМУМА ФУНКЦИИ 5 2.НЕОБХОДИМЫЕ И ДОСТАТОЧНЫЕ УСЛОВИЯ СУЩЕСТВОВАНИЯ ЭКСТРЕМУМОВ 7 3.АЛГОРИТМ НАХОЖДЕНИЯ ТОЧЕК ЭКСТРЕМУМА ФУНКЦИИ 13 4. ЭКСТРЕМАЛЬНЫЕ ЗАДАЧИ В АЛГЕБРЕ И ГЕОМЕТРИИ 16 5. ЭКСТРЕМАЛЬНЫЕ ЗАДАЧИ В ДРУГИХ НАУКАХ 35 ЗАКЛЮЧЕНИЕ 42 СПИСОК ЛИТЕРАТУРЫ 44 ВВЕДЕНИЕЭкстремальные задачи – задачи на максимум и минимум – играют большую роль в нашей жизни. С такими задачами приходится иметь дело представителям самых разных специальностей. Инженеры-технологи стараются так организовать производство, чтобы выпускалось как можно больше продукции; конструкторы пытаются разработать прибор для космического корабля так, чтобы его масса была наименьшей; экономисты стараются спланировать связи завода с источниками сырья так, чтобы транспортные расходы оказались минимальными и т.д. Каждая организация сталкивается с необходимостью сделать определенную работу, затратив как можно меньше ресурсов. Здесь и приходят на помощь методы решения задач оптимизации, о которых и пойдет речь в моей работе. Существование этих задач и методы их решения являются ярчайшим примером необходимости математики в нашей жизни. Развитие областей науки и техники существенно зависит от развития различных направлений математики. В настоящее время математика становится средством решения проблем организации производства, помогает в поиске оптимальных решений, что содействует повышению производительности труда. Многие прикладные задачи сводятся к исследованию функции на экстремум. В частности, в экономической теории задача математического программирования часто сводится к задаче на условный экстремум. Одним из наиболее удобных способов поиска экстремума функции при наличии ограничений на ее переменные, т.е. решения задачи условной оптимизации, является метод множителей Лагранжа. Основное практическое значение метода Лагранжа заключается в том, что он позволяет перейти от условной оптимизации к безусловной. Курс алгебры содержит разнообразный материал, однако, одним из его разделов является вопрос о нахождении экстремальных значений. Между тем знание способов решения подобного рода задач оказывается полезным при решении многих текстовых задач, т.к. может значительно облегчить их решение. Решение задач за экстремумы имеет не только теоретический интерес. К решению таких задач сводятся иногда задачи, связанные с практикой и повседневной деятельностью человека. Также такие уравнения иногда встречаются в физике и геометрии. Все выше сказанное подчеркивает актуальность выбранной темы курсовой работы. Целью исследования является систематизация и обобщение методов решения задач на экстремумы из различных предметных областей. Объектом исследования стали методы математического анализа. Предмет исследования – задачи на нахождение экстремальных значений величин и методы их решения. Цель, объект и предмет исследования обусловили выбор следующих задач: - рассмотреть понятие экстремума функции, изучить локальный и глобальный экстремум, а также точки экстремума функции; - изучить необходимые и достаточные условия существования экстремума функции; - охарактеризовать алгоритм нахождения точек экстремума функции; - рассмотреть экстремальные задачи в курсе алгебре и геометрии; - выделить особенности экстремальных экономических и производственных задач; - рассмотреть экстремальные задачи в других науках. Курсовая работа курсовая работа курсовая работа курсовая работа ПОНЯТИЕ ЭКСТРЕМУМА ФУНКЦИИ. ЛОКАЛЬНЫЙ И ГЛОБАЛЬНЫЙ ЭКСТРЕМУМ. ТОЧКИ ЭКСТРЕМУМА ФУНКЦИИЭкстремумом функции называется максимальное (минимальное) значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Точка 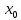 называется точкой локального максимума функции f(x), если выполняется условие: называется точкой локального максимума функции f(x), если выполняется условие:  Аналогично точка 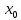 называется точкой локального минимума функции называется точкой локального минимума функции 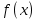 , если выполняется условие: , если выполняется условие:  Точки, в которых производная равна нулю, называются стационарными точками. Точки, в которых функция непрерывна, а её производная либо равна нулю, либо не существует, называются критическими точками.1 Нахождение экстремумов функции может быть как самостоятельной задачей, так и одним из этапов полного исследования функции и построения её графика. 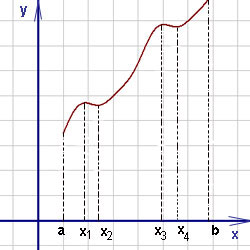 рис. 1 Точки экстремума - объединяющий термин для точек максимума и минимума, а значения функций в этих точках называются экстремумами функции. Рассмотрим график непрерывной функции. Из рисунка 1 видно, что значение функции в точке 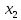 меньше, чем значения функции в достаточно близких к ней точках, соседних с ней справа и слева. В этом случае говорят, что функция имеет в точке меньше, чем значения функции в достаточно близких к ней точках, соседних с ней справа и слева. В этом случае говорят, что функция имеет в точке 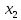 минимум. минимум.В точке 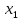 значение функции больше значений функции в достаточно близких к ней точках, расположенных справа и слева от неё. В этом случае говорят, что функция имеет в точке значение функции больше значений функции в достаточно близких к ней точках, расположенных справа и слева от неё. В этом случае говорят, что функция имеет в точке 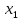 максимум. максимум.Приведем строгие определения точек экстремума. Определение 1: Функция 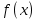 имеет минимум в точке имеет минимум в точке 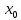 , если существует такая окрестность точки x0, что для всех , если существует такая окрестность точки x0, что для всех  из этой окрестности выполняется неравенство из этой окрестности выполняется неравенство  Определение 2: Функция 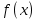 имеет максимум в точке имеет максимум в точке 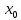 , если существует такая окрестность точки , если существует такая окрестность точки 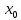 , что для всех , что для всех  из этой окрестности выполняется неравенство из этой окрестности выполняется неравенство  Из приведённых определений следует, что экстремум функции имеет локальный характер - это наибольшее и наименьшее значение функции по сравнению с близлежащими значениями. На промежутке функция может иметь несколько экстремумов, причём может оказаться, что какой-либо минимум функции больше какого-либо ее максимума. Так, для функции, изображённой на рисунке 1, 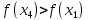 . .Следующая теорема позволяет ответить на вопрос, в каких точках функция может достигать экстремума. |
