Понятие экстремума функции. Локальный и глобальный экстремум. Точки экстремума функции
 Скачать 218.52 Kb. Скачать 218.52 Kb.
|
АЛГОРИТМ НАХОЖДЕНИЯ ТОЧЕК ЭКСТРЕМУМА ФУНКЦИИОпределение 3. Точкой максимума (минимума) функции 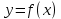 называется значение аргумента называется значение аргумента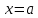 такое, что существует окрестность точки такое, что существует окрестность точки 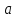 , в которой , в которой 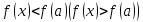 для для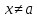 . . Определение 4. Максимумом (минимумом) функции называется её значение в точке экстремума, т.е. величина 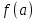 . .Таким образом, если в задании стоит требование определить точки экстремума в ответе следует писать найденные значения 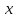 , если нужно указать сами экстремумы, то нужно определить значения y в этих точках, подставив их в формулу функции , если нужно указать сами экстремумы, то нужно определить значения y в этих точках, подставив их в формулу функции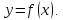 5 5Что касается наибольшего или наименьшего значения функции на заданном отрезке, то для непрерывной функции они могут достигаться как внутри отрезка, так и на его концах. Если наибольшего (наименьшего) значения функция достигает во внутренней точке отрезка, то эта точка совпадает с точкой соответствующего экстремума. Для ответа на такой вопрос следует сравнить значения функции в точках экстремума с её значениями на концах отрезка. (На практике для решения этой задачи не обязательно определять вид экстремума, достаточно вычислить значения функции в критических точках и на концах отрезка и сравнить их между собой.) Рассмотрим задачи на нахождение точек экстремума функции. Алгоритм нахождения точек экстремума. 1) Найти область определения функции. 2) Найти производную функции f '(x). 3) Найти точки, в которых f '(x) не существует. 4) Найти точки, в которых f '(x) = 0. 5) Отметить на числовой прямой область определения функции и все точки, выявленные в п. 3 и п. 4. Получатся промежутки области определения, на которых производная сохраняет постоянный знак. 6) Определить знак f '(x) для каждого промежутка. (Чаще всего это делается подстановкой "удобного" значения x из этого промежутка в полученную в п. 2 формулу для производной.) 7) Определить по знакам производной участки возрастания и убывания функции и сделать выводы о наличии или отсутствии экстремума и его характере в каждой из критических точек. Задача 6. Найдите точку максимума функции 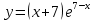 1) Функция представляет собой произведение линейной и показательной функций, которые определены на всей действительной оси. 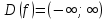 2) Вычисляем производную, пользуясь правилом дифференцирования произведения и формулами для производной степенной и показательной функций. 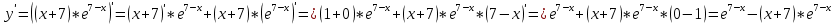 Вычисление производной завершено, но для облегчения действий в следующих пунктах, стоит преобразовать её к наиболее компактному виду. 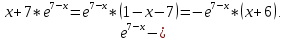 Итак, 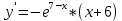 3) Выражение  определено во всех точках действительной оси. определено во всех точках действительной оси. Точек, где 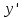 не существует, нет. не существует, нет.4) Решаем уравнение 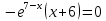 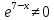 при любых значениях x, при любых значениях x,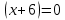 при при 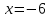 . .5) Изображаем "бесконечную" числовую ось, совпадающую в нашем случае с областью определения функции. Отмечаем на ней единственную найденную критическую точку 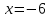 . .6) Определяем знаки производной на получившихся двух участках оси. При 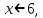 например при например при 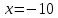 , имеем , имеем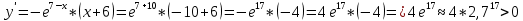 При 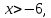 например при например при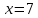 , имеем , имеем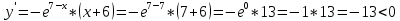 Отмечаем на оси знаком "+" участок, где 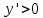 и знаком "−", где и знаком "−", где 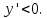  7) На участках, где производная положительна, функция возрастает, а где производная отрицательна, функция убывает. Расставляем на рисунке соответствующие стрелочки. По стрелочкам видно, что в точке 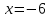 функция переходит от возрастания к убыванию, значит это и есть искомая точка максимума. функция переходит от возрастания к убыванию, значит это и есть искомая точка максимума.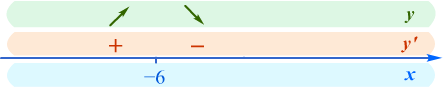 Ответ: −6 |
