Практическая значимость применения математических знаний
 Скачать 371.59 Kb. Скачать 371.59 Kb.
|
ВВЕДЕНИЕМатематика в различных профессиях, имея разную степень использования, лишь в одном может быть определяющей, когда она используется в профессиях, от которых зависит безопасность и жизнь других людей. Такой степенью ответственности обладает математика в профессии железнодорожника. При проектировании сложных транспортных сооружений от действия любых видов статических и динамических нагрузок требуется проведение большого количества вычислений. Основой вычислительного эксперимента являются математическая модель. Решение каждой из проставленных задач в настоящее время – это знание и применение численных методов расчета. Целью данного проекта является изучение значимости применения математики на железной дороге. Для достижения поставленной цели необходимо решить следующие задачи: рассмотреть практическую значимость применения математики; изучить основные показатели, применяемые в отношении работы на железной дороге; проанализировать области практического применения расчетов на железной дороге; привести примеры решения задач. Объект исследования: математические задачи. Предмет исследования: применение математических знаний в железнодорожном транспорте. Методы исследования: кро аплро Продукт работы: ТЕОРЕТИЧЕСКАЯ ЧАСТЬПрактическая значимость применения математических знаний В развитии различных областей человеческой деятельности математика оказывала и оказывает существенное влияние. Ее роль складывалась исторически и зависела от двух факторов: степени развития математических понятий и математического аппарата, а также степени зрелости знания об изучаемом объекте. Современное развитие науки характеризуется потребностью изучения сложных всевозможных процессов и явлений – физических, химических, биологических, экономических, социальных и других. Теории математики широко применяются в других науках, казалось бы, совершенно от нее далеких – лингвистике, юриспруденции. Развитие методов вычислительной математики и нарастание мощности компьютеров позволяют в наши дни выполнять точные расчеты в самых разных областях деятельности человека. Область применения математических законов не знает границ, они используются во многих отраслях науки и производства. Строительные задачи могут отличаться по степени сложности расчетов. Например, прочностные расчеты, определяющие геометрию основных элементов здания и степень выносливости несущих конструкций, относятся к сложнейшим вычислениям. Подобные расчеты выполняются с учетом множества факторов и стоят на стыке двух наук – математики и сопротивления материалов. Однако помимо таких сверхсложных задач существуют и более простые. По данным элективного курса «Человек. Математика. Железная дорога», говорится, что овладение практически любой профессией требует разнообразных знаний по математике [6]. Особое значение имеет умение смоделировать реальные ситуации с помощью математики. Данное умение интегрирует в себе разнообразные специальные умения, адекватные отдельным элементам математических знаний, их системам, а также различные мыслительные приёмы, характеризующие культуру мышления, вырабатывает умение выделять главное, обобщать, сравнивать, анализировать. Железная дорога – это одна сплошная математика. Люди сталкиваются с математикой уже при покупке билета. Стоимость билета, номер места, время отправления и прибытия на конечный пункт – это все математика [2]. Расстояние, время следования в пути, количество остановок, вагонов, нумерация вагонов. В самом вагоне: количество ступенек при поднятии в вагон, мест в вагоне, купе, мест в купе, мест на боковых местах, окон, туалетов в вагоне. При возврате постельного белья проводнику обязательно должны сдать две простыни, одну наволочку и одно полотенце. Покупая чай или кофе, в ход идут уже деньги, а деньги любят счет. Теперь сам вокзал обязательно предусматривает наличие нескольких платформ и нескольких путей. Например, 3-я платформа 5-й путь, слышишь объявление диспетчера. Это тоже математика. И это лишь малая часть математики на железной дороге. Сооружению каждого километра железной дороги предшествует упорный труд людей – тех людей, которые должны рассчитать и спроектировать каждый шаг строительства. Строительство дороги начинается с экономических расчетов, целью которых является определение размеров и характера предстоящих перевозок, т.е. составляется техническое задание на проектирование железной дороги. Сооружая дорогу, строители стремятся сделать ее как можно дешевле, а значит, рассчитывается объем земельных работ, сколько кубов необходимо для насыпей, рассчитывают крутизну дороги. Стремление к быстрому преодолению расстояний – одна из естественных потребностей человека. Поэтому борьба за скорость на железных дорогах ведется с момента их возникновения, и в этом помогают знания и понимание математического анализа [https://www.informio.ru/publications/id3734/Primenenie-matematiki-v-razlichnyh-sferah-chelovecheskoi-dejatelnosti]. [2] ССЫЛКА ПО ОБРАЗЦУ Основные показатели работы железнодорожного транспортаПродукция железнодорожного транспорта оценивается целым рядом количественных и качественных показателей. Количественные показатели характеризуют объем перевозочной работы. Одним из основных установлен количественный показатель ЕP — объем перевозок (по отправлению) грузов, в тоннах (т), обычно за год, утверждаемый для сети железных дорог правительством. Этот показатель обеспечивает лучшую увязку планов производства с планами перевозок единым измерением — тоннами — по сравнению с показателем грузооборота в тонно-километрах, считавшимся основным до 1982 г. Вторым основным количественным показателем является грузооборот Pl — в тонно-километрах (т*км), представляющий собой произведение массы перевозимых грузов на расстояние (дальность) /перевозки. Грузооборот является обобщающим показателем, планируемым на всех уровнях, и используется для определения потребности в подвижном составе и ремонтной базе, затратах труда, топлива, электроэнергии и т.д. В целях сокращения расходов на перевозки и ускорения доставки грузов план грузооборота должен выполняться за счет роста количества перевозимого груза, а не за счет увеличения дальности перевозок [1]. К числу важнейших количественных показателей относится количество перевезенных пассажиров Аl обычно за год, а также пассажирооборот Аl, исчисляемый в пассажиро-километрах (пасс. - км) и представляющий собой сумму произведений числа перевезенных пассажиров на среднее расстояние перевозки. Приведенная продукция железнодорожного транспорта, исчисляемая в приведенных тонно-километрах, определяется по формуле: Е lпр=Е Pl + k Е (1); (https://studall.org/all4-49343.html) [2] ПО ОБРАЗЦУ где k — коэффициент перевода пассажиро-километров в тонно-километры. Коэффициент перевода определяется соотношением себестоимости перевозок одного тонно километра и одного пасс. км. При определении производительности труда на железнодорожном транспорте значение к в большинстве случаев принимают равным 2, что соответствует учету труда на выполнение грузопассажирских перевозок. Грузонапряженность железных дорог определяется средним количеством выполненной тонно-километровой работы или приведенными тонно-километрами, приходящимся на один км эксплуатационной длины. Основными качественными показателями работы железных дорог и их подразделений являются: Выполнение плана перевозок, графика движения и плана формирования поездов; Техническая, участковая и маршрутная скорость движения поездов; Степень использования подвижного состава: оборот вагона и локомотива, статическая, динамическая нагрузка и производительность грузового вагона. Важнейшим качественным показателем на железнодорожном транспорте, отражающим работу всех основных подразделений дорог, являются оборот вагона, представляющий собой время от начала погрузки вагона до начала следующей его погрузки. К обобщающим экономическим показателям работы железнодорожного транспорта относятся производительность труда, себестоимость перевозок и прибыль. Производительность труда определяется объемом выполненной продукции, приходящимся на одного работника эксплуатационного штата, исчисляемом в тонно-километрах, пассажиро-километрах или приведенных тонно-километрах. Себестоимость перевозок представляет собой отношение суммы эксплуатационных расходов по перевозке к объему выполненной продукции. Прибыль определяется как разность между суммарными доходами железной дороги или отделения дороги и суммой эксплуатационных расходов на выполнение перевозок за тот же период времени. Прибыль — это показатель, в котором аккумулируются итоги всей хозяйственной деятельности железных дорог и предприятий транспорта [3]. Есть и более сложные показатели, расчеты которых служат для прогнозирования определенных воздействий. К примеру, чтобы защитить железнодорожные пути и сооружения от воздействия снежных заносов инженеру необходимо определить вид снегозащиты. Для этого он рассчитает количество снега, которое должно быть задержано, по формуле:  (2) (2)где: α – угол направления линии снегозащиты к снеговетровому потоку; t – продолжительность метели, мин; i – интенсивность переноса снега). Площадь поперечного сечения снежного вала, образующегося у этой защиты, по формуле:  (3) (3)где d – плотность снега) [2]. Таким образом, в современной железнодорожной отрасли роль математики, как мы видим, очень велика. Благодаря применению математических знаний, работа железной дороги становится более продуктивной, что влечёт за собой рост её значимости. ПРАКТИЧЕСКАЯ ЧАСТЬОбласти практического применения математики на железной дороге Цель практической части: практическая значимость применения математических знаний Железнодорожный транспорт играет главнейшую роль в перевозке разного рода грузов по сравнению с водным, автомобильным и воздушным транспортом. Железные дороги являются ключевым элементом транспортной и логистической инфраструктуры. Современный мир – это постоянное развитие, новые технологии, научные исследования и разработки, роль математики в которых постоянно возрастает. Трудно понять и освоить явления действительности без их математической модели. Математика играет большую роль и в современной железнодорожной отрасли. Строительство дороги начинается с экономических расчетов, целью которых является определение размеров и характера предстоящих перевозок, т. е. составляется техническое задание на проектирование железной дороги. Далее нужно ответить на вопрос, где лучше провести дорогу. Просчитываются технические экономические варианты [5]. Сооружая дорогу, строители стремятся сделать ее как можно дешевле, а значит, рассчитывается объем земельных работ, сколько кубов необходимо для насыпей, рассчитывают крутизну железных дороги. При строительстве каждой железной дороги устанавливается наибольший уклон, который может преодолеть локомотив с составом заданной массы. Поэтому проводится большое количество расчетов, чтобы определить выгоду, полученную от увеличения массы поезда и уменьшение земельных работ. Нужно рассчитать, сколько кубов земли нужно убрать, и сколько кубов нужно перевести туда, где будет насыпь. Если внимательно посмотреть на состав грузового поезда, можно увидеть, что его вагоны отличаются друг от друга не только внешним видом, но и размерами. Перед железнодорожниками встала задача, как увеличить массу поезда, не увеличивая его длинны. Для этого опять требуются математические расчеты. Не обошла эта проблема и пассажирские вагоны. Они тоже требуют кропотливых расчетов. Ведь их необходимо сделать надежнее и долговечные, и при этом не израсходовать лишние материалы и не увеличить их стоимость. Математические расчеты нужны и на сортировочных горках. Продолжительность торможения зависит не только от массы вагона, но и от скорости и направления ветра, длины пути, кривизны уклона, количество стрелок и кривых, по которым пролегает путь вагона, Чтобы учесть все эти факторы, опять необходимы математические расчеты. Правильно высчитать расстояние между колеей рельсов, определить и устранить их проседание с помощью подбивки шпал, рассчитать время прибытия следующего товарного или пассажирского состава, определить допустимый зазор в буксах колесных пар – в этом и многом другом нужна математика, железнодорожнику. Строительство нового железнодорожного пути, ремонт и текущее содержание существующего пути включают в себя комплекс геодезических и инженерных, а, следовательно, и математических расчётов. Развитие железнодорожного транспорта в настоящее время невозможно представить без использования математических моделей и алгоритмов. Повысить скорости движения поездов и сократить время в пути, минимизировав при этом затраты, можно только при качественном и полном использовании математического аппарата. Использование информационных технологий позволяет принять эффективное решение при разработке проекта реконструкции железнодорожной линии. Железная дорога требует точности, исключает любые погрешности. Все должно быть слажено и взаимосвязано, например движение поездов. Каждый поезд движется строго по расписанию. Специалисты, которые занимаются его составлением, должны знать свойства функций, способы построения графиков, комбинаторику и теорию графов. Применение методов компьютерной оптимизации при реконструкции железных дорог позволяет найти оптимальное решение при той или иной постановке задачи без значительного увеличения материальных расходов, которые в настоящее время являются основным из важнейших критериев любого исследования [4]. При математическом моделировании железная дорога представляется в виде технической системы, которая делится на участки (перегоны и раздельные пункты), в пределах которых ограничение скорости постоянно. Участок описывается множеством параметров технических устройств (верхнее строение пути, в том числе стрелочные переводы, искусственные сооружения), определяющих ограничения скорости на участке. Скорость на линии ограничена возможностями технических устройств. Ограничения скорости изменяются по длине линии [4]. Продолжительность торможения зависит не только от массы вагона, но и от скорости и направления ветра, длины пути, кривизны уклона, количества стрелок и кривых, по которым пролегает путь вагона. Все эти факторы необходимо учитывать в математических расчетах. Таким образом, использованием аппарата математики ведется по вопросам экономики железнодорожного транспорта, рационализации управленческих, организационных и социальных систем на железных дорогах, оптимизации процесса перевозок, использования подвижного состава, организация управления вагонным хозяйством, использование вычислительной техники, сокращение расходов электроэнергии и т.д. [https://cyberleninka.ru/article/n/primenenie-metodov-matematicheskogo-modelirovaniya-pri-proektirovanii-rekonstruktsii-zheleznodorozhnogo-puti]. [2]. ПО ОБРАЗЦУ 2.2 Примеры решения задачРассмотрим типовую задачу на движение, которые требует составления уравнения, системы уравнений или неравенства на основании условия задачи. Основные компоненты: пройденный путь (s); скорость (v); время (t). Зависимость между указанными величинами выражаются формулами: s=vt; (4) v=s/t; (5) t=s/v.[ https://skysmart.ru/articles/mathematic/vremya-skorost-rasstoyanie].ССЫЛКА План решения: 1. Выбираем одну из величин, которая по условию задачи является неизвестной, и обозначаем ее через x (y или z); 2. Устанавливаем, какая из величин является по условию задачи известной; 3. Третью (из оставшихся) величину выражаем через неизвестную (x) и известную с помощью одной из формул; 4. Составляем уравнение на основании условия задачи, в котором указано, как именно изменилась (уменьшилась, увеличилась и т.д.) третья величина [6]. Задача 1. Из города А в город В, расстояние между которыми 300 км, выехал автобус. Через 20 мин навстречу ему из В в А вышел электропоезд и через 2 часа они одновременно прибыли на станцию М. С какой скоростью шел электропоезд, если она была на 20 км /ч больше скорости автобуса? Решение: 1. Принимаем за х скорость электропоезда; 2. Скорость автобуса (х - 20) км/ч; 3. 20 минут = 20/60 часа = 1/3 часа. 4. Автобус выехал из города раньше на 1/3 часа, поэтому до встречи с электропоездом ехал: 2 +1/3 = 7/3 часа. 5. Составим уравнение и решим его: 2х +7/3(х - 20) = 300; 2х + (7х - 140)/3 = 300; 6х +7х - 140 = 900; 13х = 1040; х = 80. Ответ: скорость электропоезда составляла 80 км/ч. Далее рассмотрим типовую задачу на производительность труда железнодорожных работников. Задача 2. Две ремонтные бригады Вагонной части депо выполнили работу по ремонту букс за 4 дня. За сколько дней может выполнить ремонт каждая бригада, если одной из них для выполнения этой работы потребовалось бы на 6 дней меньше, чем другой? Решение: Пусть за х дней выполнит всю работу первая бригада, за х-6 дней – другая. По условию задачи за 4 дня выполняют всю работу обе бригады. 1/х – производительность труда первой бригады; 1/х-6 - производительность труда второй бригады; 1/4 - производительность труда двух бригад вместе. Составим и решим уравнение: 1/х+1/(х-6)=1/4; 4(х-6)+4х=х(х-6); х=12; Ответ:12 дней. Рассмотрим пример расчета необходимого материала. Задача 3. Железнодорожная насыпь - прямая призма, основание равнобедренная трапеция. Основание: а=8 м, b=13 м, h= 3,2 м, Н=1 км=1000м (м³)– столько земли нужно привезти на 1кг насыпи. Для решения будем использовать следующую формулу: V = Sосн * H; Sосн = (a+b)*h/2; Sосн 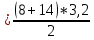 = 35, 2; = 35, 2;V = 35, 2 * 1000; V = 35200 м³. Ответ: 35200 м³. Вывод по практической части По результатам работы, можно сказать, что благодаря применению математических знаний, работа железной дороги становится более продуктивной, что влечёт за собой рост её значимости. Современный специалист не может стать профессионалом своего дела без знаний математики. ЗАКЛЮЧЕНИЕСовременное развитие науки характеризуется потребностью изучения сложных всевозможных процессов и явлений – физических, химических, биологических, экономических, социальных и других. Теории математики широко применяются в других науках, казалось бы, совершенно от нее далеких. Развитие методов вычислительной математики и нарастание мощности компьютеров позволяют в наши дни выполнять точные расчеты в самых разных областях деятельности человека. В современной железнодорожной отрасли роль математики, как мы видим, очень велика. Благодаря применению математических знаний, работа железной дороги становится более продуктивной, что влечёт за собой рост её значимости. Использованием аппарата математики ведется по вопросам экономики железнодорожного транспорта, рационализации управленческих, организационных и социальных систем на железных дорогах, оптимизации процесса перевозок, использования подвижного состава, организация управления вагонным хозяйством, использование вычислительной техники, сокращение расходов электроэнергии и т.д. По результатам работы, можно сказать, что благодаря применению математических знаний, работа железной дороги становится более продуктивной, что влечёт за собой рост её значимости. Современный специалист не может стать профессионалом своего дела без знаний математики. Подводя итог работы, можно отметить, что для формирования профессиональных компетенций будущих железнодорожников требует наличия высокого уровня математических знаний. Формирование навыков моделировать жизненные ситуации с помощью инструментов математической науки способствуют развитию технического мышления. СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫЕфименко Ю.И. Железные дороги. Общий курс: учебник / Ю.И. Ефименко, В.И. Ковалев, С.И. Логинов и др.; под ред. Ю.И. Ефименко. - 6-е изд., перераб. и доп. - М.: «Учебнометодический центр по образованию на железнодорожном транспорте», 2018. - 503 с; Крейнис З.Л., Селезнёва Н.Е. Техническое обслуживание и ремонт железнодорожного пути: учебник. – М.: «Учебно-методический центр по образованию на железнодорожном транспорте», 2017. – 568 с. 3; Крейнис З.Л., Федоров И.В. Железнодорожный путь. Учебник для техникумов и колледжей ж.-д. транспорта. М,: УМК МПС России 2016 – 368 с; Лазарев А.А., Мусатова Е.Г., Гафаров Е.Р., Кварацхелия А.Г. Теория расписаний. Задачи железнодорожного планирования /Научное издание. — М.: ИПУ РАН, 2016. — 92 с; Лецкий Э.К. Информационные технологии на железнодорожном транспорте. - М.: УМК ПМС России, 2017; Элективный курс «Человек. Математика. Железная дорога» – Электронный ресурс. Режим доступа: http://festival.1september.ru/articles/633749/ |
