планэкс(Изначальный). Практикум и пособие для выполнения домашнего задания и курсовой работы для специальности 1105
 Скачать 0.77 Mb. Скачать 0.77 Mb.
|
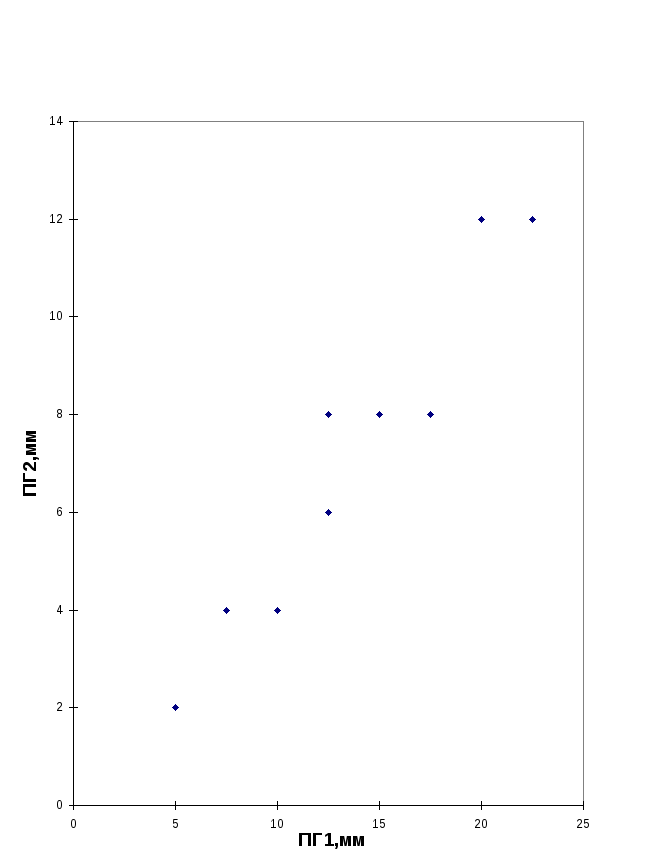 Рис.2.2. Корреляция между стандартными (ПГ1) и лабораторными (ПГ2) показателями горячеломкости ЛАБОРАТОРНАЯ РАБОТА N3 ИСПОЛЬЗОВАНИЕ ФУНКЦИИ ЖЕЛАТЕЛЬНОСТИ ДЛЯ ВЫБОРА СПЛАВА С ОПТИМАЛЬНЫМ СОЧЕТАНИЕМ РАЗЛИЧНЫХ ПОКАЗАТЕЛЕЙ КАЧЕСТВА (2 ч ) 1. ЦЕЛЬ РАБОТЫ Научиться использовать функцию желательности для решения задач, связанных с достижением наилучшего комплекса различных параметро оптимизации. Ознакомиться с использованием языка программирования QuickBASIC для расчета функции желательности.
В подавляющем большинстве случаев при проведении исследовательских работ по выбору оптимального состава сплава (или технологических параметров) необходимо определить наилучший комплекс различных показателей (прочности, твердости, пластичности, вязкости разрушения, коррозионной стойкости, жаропрочности, литейных характеристик, обрабатываемости резанием, свариваемости и т.д.). Одни сплавы имеют более высокий уровень одних показателей (например, прочности); другие сплавы - других (например, пластичности). Из этого следует, что выбор оптимального состава непосредственно по результатам эксперимента сделать обычно нельзя, особенно при большом количестве параметров оптимизации. В этом случае целесообразно использовать функцию желательности как обобщенный показатель качества, который и служит мерой сравнения разных сплавов (или технологических параметров). Сущность данного метода заключается в том, что различные показатели качества с разной размерностью переводятся в соответствующие безразмерные желательности (d), после чего рассчитывают обобщенную фукцию желательности (D): где n- число параметров оптимизации. Таким образом, величина D становится единственным параметром оптимизации. Под желательностью di понимают задаваемый уровень желательности, который может меняться в пределах от 0 до 1: d=1 - максимально возможный уровень качества d=1-0.8 очень хороший уровень качества d=0.8-0.6 хороший уровень качества d=0.6-0.37 допустимый и достаточный уровень качества d=0.37 заданный уровень качества d=0.37-0 недопустимый уровень качества Возможны два варианта перевода значений параметра оптимизации всоответствующие желательности. В случае односторонних ограничений Y>Ymin или Y d= (3.2) где y’ - безразмерная величина, которая линейно (реже нелинейно) связана с Y . Если ограничения двусторонние Ymin функция желательности задается выражением: d= (3.3) где y =(2Y -(Y +Y ))/(Y -Y ), а n- целое положительное число, вычисляемое после задания свойству желательностей (в интервале 0.6-0.9). После определения y по уравнению 3.3 вычисляют n: n=lnln(1/d)/ln (y ). Выбирая разные значения n, можно получать различную кривизну функций желательности, общий вид которых показан на рис.3.1. При использовании функции желательности наиболее ответственным этапом является выбор реперных точек. Обычно это определение 2-х уровней: d=0,37 и d=0,6-0,8, т.е. удовлетворительного и хорошего. Первому уровню может соответствовать требование технического задания, а второму- реально достижимый максимальный уровень. Например, если требуется разработать литейный алюминиевый сплав с пределом текучести (0.2 ) не ниже 300 МПа и показателем жидкотекучести по прутковой пробе (ПЖ) не ниже 350 мм, то можно выбрать следующие реперные точки: 1- d =О.37 0.2=300 МПа и ПЖ=350 мм;
В этом случае превышению минимального уровня до второй реперной точки будет отвечать сильный почти линейный рост d, а при дальнейшем росте значений 0.2 и ПЖ увеличение d будет менее существенным. Очевидно, что при решении конкретных задач значение d<0.37 недопустимо для любого показателя. В последнем случае сплав необходимо улучшать (модифицировать) с целью достижения заданных требований. Используя значения функции желательности, можно выбрать сплав наилучшим образом отвечающий этим требованиям, что позволяет максимально сократить стадию его доработки. При выполнении поисковой исследовательской работы, когда требования к конкретным показателям жестко не определены (например, задача заключается в выборе перспективной области составов), выбор параметров оптимизации и реперных точек более произволен и в значительной мере зависит от того, как исследователь представляет проблему. Например, если из пяти рассматриваемых свойств три являются характеристиками прочности, то наилучшим значением D скорее всего будет обладать наиболее прочный сплав, и наоборот если будут рассматривать в основном литейные свойства - то лучшим окажется другой сплав. Из этого следует, что выбор свойств и соответствующих им реперных точек при решении таких задач является процедурой, трудно поддающейся формализации. Однако, если задача уже конкретно сформулирована, то использование функции желательности для ее решения может быть очень эффективным.
I. Поставлена задача разработать новый алюминиевый сплав, к которому предъявляются следующие требования: 1- временное сопротивление в,МПа - не ниже 400 МПа; 2- твердость - не ниже 120 НВ и не выше 160 НВ 3- относительное удлинение - не ниже 3%; 4- горячеломкость по кольцевой пробе ВИАМ (ПГ) -не более 15 мм; 5- коэффициент термического расширения (КТР)- не более 22.5 *10-6 1/С. Данные значения следует использовать в качестве реперных точек для удовлетворительного уровня (y'=0; d=0,37). Для хорошего уровня (y'=1; d=0,7) рекомендуются следующие значения: в =600 МПа; =10%;ПГ=7.5 мм и КТР=20*10--6 1/ С. Для твердости, имеющей двустороннее ограничение, рекомендуется задать значению 130 НВ, уровень желательности d=0,7. II. Задача, сформулированная в п. I, имеет другие исходные данные (в скобках хороший уровень d=0.7): 1- временное сопротивление в ,МПа - не ниже 200 МПа (280 МПа) ; 2- твердость - не ниже 80 НВ и не выше 120 НВ (93 НВ) 3- относительное удлинение - не ниже 1,5% (3%); 4- горячеломкость по кольцевой пробе ВИАМ (ПГ) -не более 10 мм (5 мм); 5- коэффициент термического расширения (КТР)- не более 20 *10-6 1/С (18.5 *10-6 1/С) В результате проведенной работы было предложено 3 сплава с различным сочетанием заданных характеристик (см. варианты задания) 1. По имеющимся данным с использованием ЭВМ определить желательности всех заданных показателей (d1 ...d5 ) для всех сплавов (для двух вариантов) и рассчитать обобщенную функцию желательности (D).
1. Привести все расчетные формулы, связанные с определением функции желательности, с расшифровкой всех обозначений. 2. Привести графики функции желательности для односторонних и двусторонних ограничений. 3. Привести в виде таблицы исходные экспериментальные данные и рассчитанные значения di и D.
5. ЛИТЕРАТУРА
6. КОНТРОЛЬНЫЕ ВОПРОСЫ 1. Что такое желательность параметра оптимизации и в каких пределах она может меняться? 2. Что показывает обобщенная функция желательности? 3. Что означают следующие уровни желательности: d=0.37; d=1; d=0v 4. Что такое реперные точки и как они задаются? 5. В каком случае выше значение обобщенной функции желательности, рассчитанной по четырем показателям: при среднем уровне всех свойств (около заданного) или при очень высоким уровне трех показателей (d=0.9-1) и низком значении четвертого (d=0.001). 6. Что такое двусторонние и односторонние ограничения параметра оптимизации? 7. Чем руководствуются при выборе реперных точек?
а 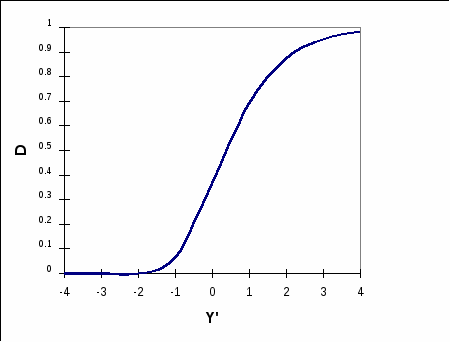 б 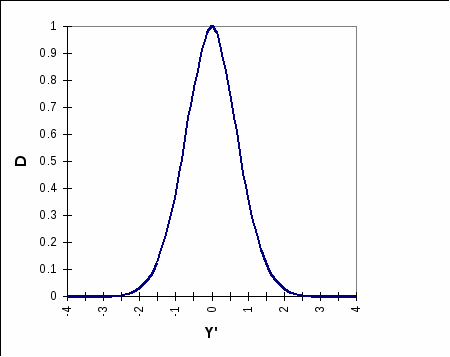 Рис.3.1. Функция желательности для односторонних (а) и двухсторонних (б) ограничений ЛАБОРАТОРНАЯ РАБОТА N4 ПОСТРОЕНИЕ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ ЗАВИСИМОСТЕЙ СОСТАВ-СВОЙСТВО МЕТОДОМ СИМПЛЕКСНОГО ПЛАНИРОВАНИЯ (4 ч)
Освоить метод симплекс- п ланирования для построения математических моделей состав-свойство многокомпонентных систем. Ознакомится с компьютерной программой "СИМПЛЕКС" для решения различных задач, связанных с симплекс-планированием. 2. ТЕОРЕТИЧЕСКОЕ ВВЕДЕНИЕ Симплекс- простейшая выпуклая геометрическая форма, образованная множеством q точек в (q-1)- мерном пространстве и обладающая минимальном количеством вершин. Симплекс является правильным, если расстояния между всеми его вершинами равны. Треугольник - двумерный симплекс, тетраэдр -трехмерный, (q-1)-мерный симплекс задает состав q-мерной системы, в частности составы тройных сплавов задают с помощью треугольника, а четверных - с помощью тетраэдра, поэтому использование симплексов для изучения зависимостей состав-свойство в соответствующих системах представляется естественным. Наиболее простые и распространенные - симплекс-решетчатые планы, в которых экспериментальные точки располагаются симметрично по симплексу (рис.4.1). По результатам определения изучаемого параметра оптимизации (Y) в точках симплекса q-мерной системы строят математические модели зависимости Y=f?X ,X ...X ) в виде полиномов различной степени. Для тройной системы A-B-C данные модели имеют следующий вид: полная 2-ая степень - 6 опытов (рис.4.1а) Y=1 X1+ 2 X2 +3 X3+ 12 X1X2 +13 X1X3 + 23 X2X3 (4.1) неполная 3-ая степень - 7 опытов (рис.4.1б) Y=1 X1+ 2 X2 +3 X3+ 12 X1X2 +13 X1X3 + 23 X2X3 + 123 X1X2X3 (4.2) полная 3-ая степень- 10 опытов (рис.4.1в) Y=1 X1+ 2 X2 +3 X3+ 12 X1X2 +13 X1X3 + 23 X2X3 + 123 X1X2X3+12 X1X2 (X1-X2) +13 X1X3 (X1-X3)+ 23 X2X3 (X2-X3) (4.3) неполная 4-ая степень- 9 опытов (рис.4.1г) Y=1 X1+ 2 X2 +3 X3+ 12 X1X2 +13 X1X3 + 23 X2X3+1 X12 X2 X3 +2 X22 X1 X3 + +3 X32 X1 X2 (4.4) полная 4-ая степень- 15 опытов (рис.4.1е) Y=1 X1+ 2 X2 +3 X3+ 12 X1X2 +13 X1X3 + 23 X2X3 +1 X12 X2 X3 +2 X22 X1 X3 + 3 X32 X1 X2 +12 X2) +13 X1X3 (X1-X3)+ 23 X2X3 (X2-X3) +12 X1X2 (X1-X2)2 + 13 X1X3 (X1-X3)2+ 23 X2X3 (X2-X3)2 (4.5) где X1 ,X2 ,X3 - концентрации компонентов A,B,C в долях от единицы (X1 +X2 +X3) =1), i , ij......- коэффициенты моделей, которые необходимо рассчитать по экспериментальным данным; Степень модели выбирают исходя из предполагаемой зависимости параметра оптимизации: чем более сложна ожидаемая зависимость - тем выше степень модели. Данные планы являются полностью насыщенными, т.е число опытов в них полностью соответствует числу определяемых коэффициентов, поэтому существуют однозначные соотношения между экспериментальными значениями Y и коэффициентами. Чем выше степень модели, тем больше требуется экспериментальных точек для ее построения (расположение экспериментальных точек показано на рис.4.1) . Если для моделей второй степени расчет коэффициентов относительно простой и может быть легко выполнен вручную (i =Yi ; ij =4Yij -2Yi -2Yj ), то в моделях более высоких степеней расчетные формулы заметно сложнее (приложение 4), что требует использования ЭВМ. После расчета коэффициентов оценивают адекватность модели, т.е. проверяют, насколько точно рассчитанные значения Y (по уравнениям 4.1-4.5) будут соответствовать истинным. Для этого необходимо знать дисперсию опыта S . Эта дисперсия может быть известна из предыдущих работ или определена экспериментальным путем (дублированием эксперимента в отдельных или во всех точках). Далее ставят контрольные опыты (эти опыты можно сделать вместе с основным экспериментом) между точками симплекса, определяют дисперсию S , а затем по критериям Фишера (F) или Стьюдента (t) определяют адекватность модели для заданного уровня значимости (обычно 0.05 или 0.01). При использовании критерия Фишера расчетное значение F определяют по формуле: F=Sост2 /Sy2 , (4.6) где Sост - остаточная дисперсия (или дисперсия неадекватности), которая рассчитывается по формуле: Sост = V(yрасч - yэксп)2/L, (4.7) где L - число контрольных опытов; yэксп ,yрасч - соответственно экспериментальное и расчетное значение параметра в i-том контрольном опыте. Гипотеза об адекватности при выбранном уровне значимости не отвергается, если выполняется условие F При использовании критерия Стьюдента расчетное значение t определяют по формуле: t= (y -y )/V (S +S ), (4.8) где S - дисперсия для i-контрольного опыта. Гипотеза об адекватности модели не отвергается, если для всех контрольных точек выполняется условие t При выборе контрольных точек обычно исходят из возможности их использования для построения моделей более высоких степеней, если построенная модель окажется неадекватной. Например, контрольные опыты для проверки адекватности модели второй степени целесообразно ставить в точках, которые соответствуют плану для модели неполной четвертой степени (рис.4.1а,в). В случае адекватной модели (F работе с цветным монитором вместо изолиний удобно использовать разные цвета, которые соответствуют заданным диапазонам параметра оптимизации. Рассмотренные зависимости можно строить не для всей системы, а только для ее части, ограниченной любым треугольником. В этом случае необходимо перевести истинные концентрации в кодовые значения, исходя из того что вершины этого треугольника представляют собой псевдокомпоненты, т.е. значение одной кодовой концентрации равно 1, а остальных 0. Например, если в системе A-B- C ограничиться областью A-10%B-10%C, то 1-ой вершиной останется компонент A (X1=1), а 2-ой и 3-ей - будут сплавы A-10%B (X2=1) и A-10%C (X3=1). В этом случае состав сплава A-5%B-2%C будет иметь следующее кодовое обозначение: X1=0.3; X2=0.5; X3=0.2. Двумерный симплекс, т.е. треугольник, можно использовать и для построения математических моделей многокомпонентных систем, если все концентрации свыше 3-х находятся на постоянном уровне. Например, составы сплавов пятикомпонентой системы A-B-C-D-E, содержащих постоянные концентрации D и E (5 и 10% соответственно) и переменные концентрации B и C (до 30 и 20 % соответственно) можно изобразить на треугольнике с вершинами: 1- A-5%D-10%E; 2- A-5%D-10%E-30%B; 3- A-5%D-10%E-20%C. 3. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ Поставлена задача изучить влияние состава на заданное свойство (Y) сплавов тройной или многокомпонентной системы (см. варианты задания). 1. По имеющимся данным построить симплекс, отметив все точки плана и контрольные точки для проверки адекватности модели. 2. Построить соотвествующую матрицу планирования в виде таблицы. 3. Используя программу СИМПЛЕКС рассчитать на ЭВМ значения коэффициентов математической модели и построить ее графическую иллюстрацию в виде линий равных значений. 4. Используя математическую модель и экспериментальные значения всех контрольных сплавов оценить адекватность построенной модели для =0,01 по F-критерию.
4. ОФОРМЛЕНИЕ ОТЧЕТА 1. Привести симплекс для изучаемой системы с точками плана и контрольными точками. 2. Привести матрицу планирования, включающую натуральные и кодовые составы экспериментальных сплавов и рассчитанные значения коэффициентов модели. 3 Привести расчетную формулу для определения параметра оптимизации (Y) в зависимости от состава сплава. 4. Привести рассчитанные значения для контрольных сплавов и результат оценки адекватности модели.
5. ЛИТЕРАТУРА
1. Что такое симплекс?
4. Какова насыщенность математических моделей в случае симплексного моделирования? 5. Сколько независимых переменных содержит уравнение математической модели в случае тройной системы? 6. Что такое кодовые значения концентраций? Как они определяются? 7. Зачем проводят оценку адекватности математической модели? 8. Что необходимо знать для оценки адекватности математической модели? 9. Что необходимо делать, если построенная модель окажется неадекватной?
|
