статистика заочн.. Практикум київ 2014 Розповсюдження і тиражування без офіційного дозволу кнтеу заборонено
 Скачать 0.97 Mb.
|
Таблиця 3.2.4Динаміка чисельності продавців овочевої продукції міста у третьому кварталі року
Визначимо середню чисельність продавців овочів у третьому кварталі за формулою середньої хронологічної для моментного ряду динаміки з рівними проміжками часу між датами. 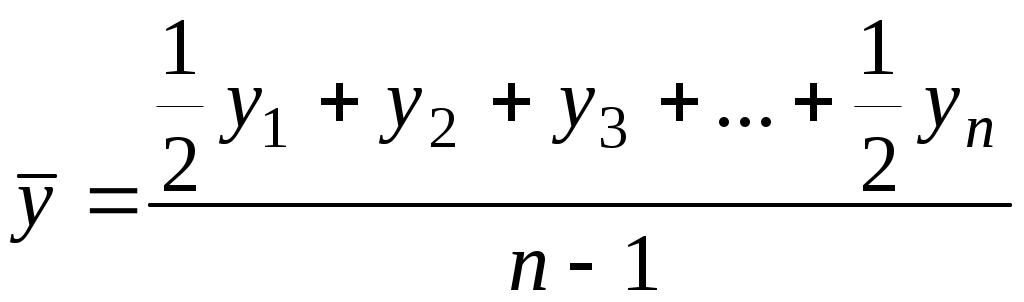 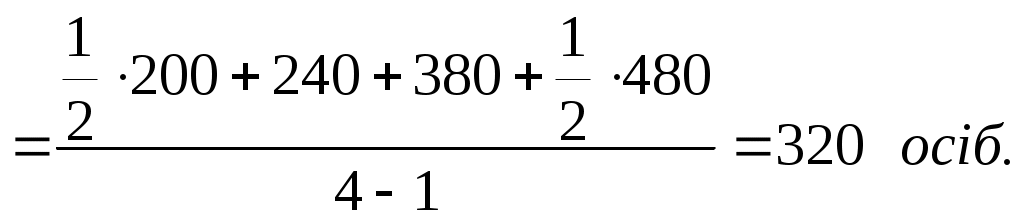  – середній рівень ряду динаміки; у – конкретні рівні ряду динаміки;п – число рівнів ряду динаміки, або число календарних дат. Якщо інтервали (проміжки часу) між датами моментного ряду динаміки неоднакові, слід використати формулу середньої арифметичної зваженої, де як ваги (частоти) беруться протяжність відрізків часу між датами, а як варіанти – парні середні суміжних значень рівнів ряду динаміки. Обчислимо середнє значення моментного ряду динаміки з нерівними проміжками часу за допомогою середньої арифметичної зваженої (табл. 3.2.5.). Таблиця 3.2.5 Динаміка вкладів населення в акціонерних банках міста
 млн грн.Обчислення можна провести і за формулою:  , де у – рівні моментного ряду динаміки, t – проміжки часу між датами. Підставимо дані табл. 3.2.5. у формулу і обчислимо середній рівень ряду: 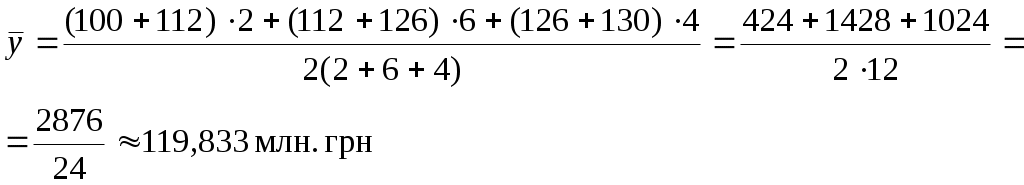 Висновок. У середньому щомісячно в акціонерних банках сума вкладів населення складала 119,833 млн грн. 3.2.9. Мода і медіана у статистиці Модою у статистиці називається ознака, яка зустрічається в досліджуваній сукупності найчастіше. Для дискретного ряду розподілу модою буде ознака, що має найбільшу частоту (f). Так, у табл. 3.2.1. мода (Мо) дорівнює 2440 грн, оскільки таку заробітну плату одержує найбільша кількість (3) працівників. В інтервальному ряді розподілу мода обчислюється за формулою:  , де Мо – мода (конкретне значення); h – величина модального інтервалу; f2 – частота модального інтервалу; f1– частота інтервалу, що стоїть перед модальним; f3– частота інтервалу, що стоїть після модального. Типова задача За даними табл. 3.2.6. визначити моду (модальний товарооборот). Таблиця 3.2.6Розподіл магазинів за обсягом товарообороту
На цьому прикладі можна побачити, що мода знаходиться в третій групі, оскільки тут найбільша частота (21 магазин). Отже, товарооборот третьої групи (1869 – 1887 тис. грн) і буде модальним. Мінімальне значення модального товарообороту (х0) дорівнює 1869 тис. грн. Величина модального інтервалу (h) дорівнює 18 тис. грн (1887 – 1869=18). Частота модального інтервалу (f2) становитиме 21 магазин. Частота інтервалу, що стоїть перед модальним (f1), дорівнює 9 магазинів, а частота інтервалу, що стоїть після модального (f3), дорівнює 15 магазинів. Підставимо наведені дані у формулу і визначимо моду:  тис. грн.Таким чином, можна зробити висновок, що в наведеній сукупності магазинів найбільш часто зустрічаються магазини з товарооборотом 1881 тис. грн. Медіаною, або серединною варіантою називається ознака, яка знаходиться у середині ранжованого ряду значень ознаки. Порядковий номер медіанної варіанти в ряді розподілу знаходиться за формулою:  , або  ,де п – число варіант;  – сума частот.Наприклад, розподіл магазинів за прибутком:
 Таким чином, медіанним буде 4-й магазин, а медіаною – його прибуток (18 тис. грн). Для парного числа магазинів (8) медіана дорівнює середній арифметичній із 4 і 5 значень ознаки. Медіана в інтервальному ряді розподілу обчислюється за формулою: 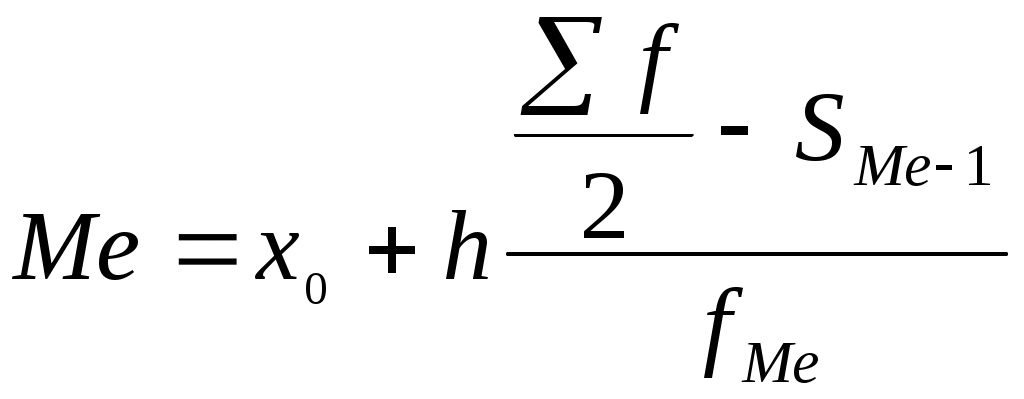 ,де  – мінімальне значення медіанного інтервалу; h – величина медіанного інтервалу;  – напівсума частот; – сума частот, що стоять перед медіанною частотою; – частота медіанного інтервалу.Типова задача Обчислити конкретне значення медіани для попередньої (табл. 3.2.6.) задачі. Спочатку слід визначити медіанний інтервал. Для цього суму частот плюс один (f+1) ділимо на 2 (54+1):2=27,5. Це означає, що медіана у ранжированому ряді буде знаходитися між 27 і 28-ю варіантами. Щоб визначити медіанний інтервал, потрібно знайти суму накопичених частот, в якій нагромаджується понад 50% чисельності ряду (3+9+21=33), тобто медіанний інтервал знаходиться у третій групі і буде дорівнювати 1869–1887, а частота цього інтервалу (21 магазин) і буде медіанною (fMe) частотою. 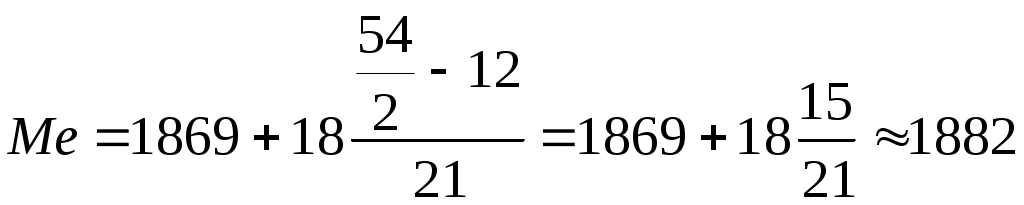 тис. грн. Таким чином, можна зробити висновок, що одна половина магазинів має товарооборот до 1882 тис. грн, а інша – понад 1882 тис. грн. 4. РЯДИ РОЗПОДІЛУ ТА ЇХ АНАЛІЗ 4.1. Ряди розподілу Статистичний ряд – це ряд чисел одержаних в процесі статистичного спостереження. Статистичний ряд, ранжирований за будь-якою ознакою називається рядом розподілу. Ряд розподілу, складений за атрибутивною ознакою, називається атрибутивним (табл 4.1). Ряд розподілу, складений за кількісною ознакою, називається варіаційним (табл. 4.2, 4.3). Варіаційні ряди прийнято поділяти надискретні (переривчасті) і неперервні. Таблиця 4.1Розподіл магазинів міста за формами власності(у % до підсумку) Атрибутивний ряд розподілу
У дискретних рядах ознаки виражені лише цілими числами без проміжних значень (табл. 4.2) Якщо варіаційний ряд характеризує розподіл одиниць сукупності за кількісною ознакою, вираженою у вигляді інтервалів, то він називається інтервальним (табл. 4.3). У неперервних рядах ознака може бути виражена не лише у цілих, але й у дробових числах. Наприклад, розподіл магазинів за рівнем виконання плану товарообороту, рентабельністю, продуктивністю праці, розподіл банків за номіналом акцій (табл. 4.4). Кожне окреме числове значення ознаки у варіаційному ряді носить назву варіанта і позначається «х». Число, яке вказує на те, скільки разів зустрічається та або інша варіанта у досліджуваній сукупності, називається частотою і позначається «f». Розподіл магазинів за кількістю працівників | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
