статистика заочн.. Практикум київ 2014 Розповсюдження і тиражування без офіційного дозволу кнтеу заборонено
 Скачать 0.97 Mb.
|
Таблиця 2.6Групування магазинів за рівнем витрат обігу
* Кожна риска відповідає одному магазину. Якщо завдання ускладнити, запропонувавши виявити залежність ціни ковбасних виробів від рівня витрат обігу, слід побудувати аналітичне групування (табл. 2.7). Таблиця 2.7Залежність середньої ціни ковбасних виробів від рівня витрат обігу
Дані таблиці свідчать, що із підвищенням рівня витрат обігу середня ціна ковбасних виробів зростає. Слід пам’ятати, що якщо із збільшенням розміру групувальної ознаки число одиниць сукупності зменшується – використовують зростаючі інтервали, а збільшується – спадаючі. Для побудови рівнонаповненого групування слід ранжирувати одиниці сукупності за групувальною ознакою і розподілити сукупність на рівні частини. Рівнонаповненим називається групування із однаковою кількістю одиниць у кожній групі. Типова задача Внаслідок спостереження одержано такі дані про кількість покупців у відділах універмагу протягом години.
Розподілити відділи універмагу на 3 групи з рівнонаповненим інтервалом за кількістю покупців. У кожну групу попадає 5 відділів (15: 3 = 5). Ранжируємо відділи за кількістю покупців і зазначаємо шифр.
За даними розшифровки легко здійснити групування відділів (табл. 2.8). Таблиця 2.8Групування відділів універмагу за кількістю покупців
2.3. Статистичні таблиці Статистичною таблицею називається форма раціонального і зв’язного викладу узагальнюючих числових показників, які характеризують різні суспільні процеси і явища (табл. 2.11). Кожна статистична таблиця має горизонтальні рядки і вертикальні графи (колонки, стовпчики). Сукупність горизонтальних рядків і вертикальних граф, а також відповідних заголовків без числових даних утворюють макет таблиці. Статистичні таблиці залежно від побудови підмету поділяються на прості, групові та комбіновані (комбінаційні). Простою називають таблицю, підмет якої містить перелік об’єктів без групування їх за будь-якою ознакою. Перелік областей України, екзаменаційні відомості, статті витрат обігу в торгівлі, відрізки часу (дати) та ін. (табл. 2.11). Груповою називається таблиця, підмет якої розбито на групи за якоюсь однією ознакою (табл. 2.8). Групування магазинів за величиною товарообороту, групування акціонерних банків за доходністю, групування студентів за віком, зростом. Комбінаційною називають таблицю, підмет якої має групування за двома і більше ознаками, пов’язаними між собою (табл. 2.4). При складанні статистичних таблиць слід дотримуватися таких правил: Кожна таблиця повинна мати загальну назву, яка розміщується над таблицею. Заголовок повинен бути точним, коротким і виразним. Заголовок має відображати: чітке визначення змісту (мети) таблиці; об’єкт, що досліджується; обмеження об’єкта в просторі і часі; іноді одиниця виміру. Кожний рядок і графа повинні мати назву. Таблиця має бути невеликою за розміром. Таку таблицю легше читати і аналізувати. Рядки в підметі і графи в присудку повинні нумеруватися. Рядки – цифрами, колонки – літерами. Суворо дотримуватися таких умовних позначень: відсутність явища, процесу, (- ), тире. відсутність даних (…), три крапки, або «нема відом.» якщо дані є, але їх числові значення менші за прийнятий у графі ступінь точності обчислення, записують 0,0 або 0,00. Абсолютні дані в межах однієї графи повинні бути округлені з однаковим ступенем точності. У таблиці спочатку розміщуються складові частини, а потім підсумок (Всього). «Всього» – остаточний результат. «Разом» – проміжний. Таблиці повинні бути замкненими, тобто мати підсумкові результати. Підсумковий рядок виділяється від основного тексту таблиці (подвійною лінією, більшою величиною інтервалу, шрифтом, кольором). 3. УЗАГАЛЬНЮЮЧІ СТАТИСТИЧНІ ПОКАЗНИКИ ТА ЗАГАЛЬНІ ПРИНЦИПИ ЇХ ЗАСТОСУВАННЯ 3.1. Абсолютні та відносні статистичні величини Абсолютними величинами називаються показники, які виражають розмір або об’єм того чи іншого суспільного явища за певний час на певній території. Наприклад, чисельність населення країни, обсяг товарообороту, величина статутного капіталу. Моментні абсолютні величини свідчать про наявність явища на певний момент часу, певну дату. Наявність населення на початок року, залишок грошей в касі на кінець робочого дня. Періодичні (інтервальні) абсолютні величини характеризують розміри, величину явища за певний проміжок часу: робочий день, тиждень, місяць, рік. Наприклад, обсяг товарообороту, кількість випущених акцій, величина валового внутрішнього продукту тощо. Основними вимірниками абсолютних величин є натуральні, умовно-натуральні, трудові та вартісні одиниці виміру. Відносними величинами у статистиці називаються узагальнюючі показники, які характеризують кількісні співвідношення між окремими ознаками суспільних явищ. Тобто, відносна величина це частка від ділення двох абсолютних величин. Відносні величини, що застосовуються у статистиці поділяють на відносні величини динаміки, планового завдання, виконання плану, структури, координації, інтенсивності. Відносними величинами динаміки, або темпами зростання, називаються показники, які характеризують зміну рівня однойменних явищ у часі. Видами відносних величин динаміки є коефіцієнти і темпи зростання, темпи приросту і середні темпи зростання та приросту. Вони обчислюються як відношення рівня звітного періоду до рівня будь-якого іншого, прийнятого за базу. Відносні величини, обчислені до якогось одного періоду, називаються базисними, а до попереднього – ланцюговими: Базисний Ланцюговий   ,де  – коефіцієнт динаміки; – рівень порівнюваного звітного періоду;У0 – рівень базисного періоду.  – рівень попереднього періоду.Коефіцієнт динаміки (зростання) показує, у скільки разів рівень звітного періоду збільшився порівняно з базисним, або попереднім. В обчисленнях базисних коефіцієнтів зростання (табл. 3.1) товарооборот кожного наступного періоду ділиться на товарооборот січня (базисного):  Ланцюгові коефіцієнти зростання обчислюються як відношення товарообороту кожного наступного місяця до попереднього:  Слід пам’ятати, що добуток усіх ланцюгових коефіцієнтів зростання дорівнює останньому базисному (1,201,251,20=1,80) і навпаки, частка від ділення кожного базисного на попередній дорівнює відповідному ланцюговому (1,8:1,5=1,2; 1,5:1,2=1,25). Таблиця 3.1 Способи обчислення відносних величин динаміки
Наявність такого зв’язку дозволяє переходити від ланцюгових коефіцієнтів до базисних і навпаки. Наприклад, у січні ціни на акції зросли на 10%, у лютому – ще на 8% і в березні – ще на 5%. На скільки процентів ціни зросли за три місяці? Просте підсумовування темпів приросту (10+8+5=23%) – неправильний результат. Наведені вище ланцюгові темпи приросту слід перетворити у коефіцієнти і перемножити їх (1,11,081,05=1,2474). Це й буде коефіцієнт зростання цін за три місяці. Тобто ціни за три місяці зросли в 1,2474 раза, досягли 124,74%, або підвищилися на 24,74%. Відносні величини планового завдання показують, у скільки разів планова величина того чи іншого показника повинна перевищувати його фактичну величину в базисному періоді:  ,де  – коефіцієнт планового завдання; – плановий рівень звітного періоду; – рівень базисного періоду.Наприклад, товарооборот магазину у звітному періоді склав 30 млн грн при плані 24 млн грн, а в базисному (минулому) році складав 20 млн. грн. Для того, щоб визначити, у скільки разів, або на скільки процентів передбачається зростання, слід обчислити .  Тобто, у звітному році порівняно з базисним товарооборот магазину передбачається (заплановано) збільшити у 1,2 раза, довести до 120%, або збільшити на 20%. Відносна величина виконання плану – це результат відношення фактичного рівня до планового:  .Відносна величина виконання плану (  ) показує,у скільки разів перевиконано план, на скільки процентів виконано план або на скільки процентів план перевиконано.Якщо фактичний обсяг товарообороту магазина ( ) складає 30 млн грн, а плановий ( ) 24 млн грн, то коефіцієнт виконання плану дорівнює 1,25. Тобто, обчислений коефіцієнт свідчить, що план перевиконано в 1,25 рази, план виконано на 125% або перевиконано на 25%. Для деяких явищ суспільного життя план передбачає не зростання, а зменшення рівня показника. Це стосується планових завдань зі зниження собівартості одиниці продукції, продуктивності праці (зменшення витрат часу на одиницю продукції) тощо. Якщо планова величина встановлюється у вигляді приростів (зниження) в абсолютних величинах, то рівень виконання плану (  ) визначається як співвідношення фактичного приросту із плановим. ,де  – фактична величина приросту,  – планова величина.Наприклад, планом передбачалося собівартість телевізора знизити на 25 грн (  ), а фактично вона знизилася на 30 грн ( ). Планове завдання зі зниження собівартості продукції перевиконано в 1,2 раза. Таким чином, план зі зниження собівартості перевиконано в 1,2 раза, виконано на 120%, або перевиконано на 20%. Якщо планове завдання пропонується у відносних величинах (коефіцієнтах або процентах) до базисного періоду, то рівень виконання плану визначається як відношення фактичного коефіцієнта зростання (  ) до планового ( ). Наприклад, прибуток підприємства у звітному періоді порівняно із базисним заплановано збільшити на 20% ( = 1,2), а збільшено на 26% ( = 1,26). Таким чином  , тобтоплан перевиконано в 1,05 раза; план виконано на 105%; план перевиконано на 5%. Якщо характер показника передбачає не його зростання, а зменшення (собівартість одиниці продукції, затрати праці на одиницю продукції, матеріалоємність продукції), то: перевищення фактичної величини над плановою є свідченням невиконання плану; якщо ж фактична величина менша за планову – це є свідченням перевиконання плану. Так, якщо собівартість (ціну) продукції в звітному періоді порівняно із базисним планували знизити на 25% ( = 0,75), а знизили на 30% ( = 0,70), то рівень виконання плану зі зниження собівартості визначається як відношення  .У такому разі стверджується, що план зі зниження собівартості продукції перевиконано на 6,7%. Якщо ж собівартість планували знизити на 20% ( = 0,8), а знизили на 12% ( = 0,88), то план зі зниження собівартості продукції недовиконано на 10%. Між відносними величинами планового завдання, виконання плану і динаміки, виражених у коефіцієнтах, існує така залежність: Добуток відносної величини планового завдання на відносну величину виконання плану дорівнює відносній величині динаміки.  Якщо відомі два із трьох названих показників, завжди можна визначити третій.  ;  ;  Типова задача. Прибуток магазину заплановано збільшити із 20 тис. грн у минулому році ( ) до 24 тис. грн у звітному році ( ), або на 20%. Фактично він зріс на 50% порівняно із минулим роком і досяг 30 тис. грн ( ). На скільки процентів перевиконано план?Розв’язання за допомогою відносних величин: = 1,2 [план = ( +20%)] = 1,5 [факт = ( +50%)]  Відповідь: план перевиконано на 25%. Відносні величини структури характеризують склад сукупності, її структуру. Обчислюються вони переважно у процентах до підсумку:  , де  – кількість одиниць сукупності з однаковою ознакою;  – загальна кількість одиниць сукупності.Наприклад, у магазині 25 продавців. Серед них 8 осіб – чоловічої статі, 17 – жіночої. Частка осіб чоловічої статі становитиме 32% (8100/25), а жіночої – 68% (17100/25). 3.2. Середні величини та загальні принципи їх застосування 3.2.1. Середня арифметична проста Припустімо, що п’яти працівникам нараховано заробітну плату 2400, 2440, 2480, 2580 і 2600 грн, а вирішено усім заплатити порівну, тобто виплатити середню зарплату. Для визначення середньої заробітної плати слід дізнатися, скільки її нараховано усім працівникам і одержану суму розділити на кількість працівників, тобто здійснити такі обчислення:  Підставимо замість чисел умовні позначення: =  грн.Це і буде формула середньої арифметичної простої, в якій по чисельнику записується сума варіант (  ), а по знаменнику – число варіант ( ), де  – середнє значення ознаки,  – варіанта (конкретне значення ознаки), – число варіант (ознак),  – знак додавання (підсумовування). Середня арифметична проста використовується тоді, коли кожна варіанта (ознака) зустрічається у сукупності один або однакове число разів. Якщо ж окремі значення ознаки (варіанти) повторюються неоднакове число разів, то середня визначається за формулою середньої арифметичної зваженої. 3.2.2. Середня арифметична зважена Середня арифметична зважена визначається за формулою:  , де – середнє значення ознаки; – варіанта;  – частота.Візьмемо такий приклад. Десяти працівникам нараховано таку заробітну плату (табл. 3.2.1): Таблиця 3.2.1 Розподіл працівників за величиною заробітної плати
Для визначення середньої заробітної плати потрібно фонд заробітної плати усіх працівників (24860 грн) розділити на чисельність працівників (10), тобто зробити обчислення: = грн.3.2.3. Обчислення середньої із інтервального ряду розподілу Щоб обчислити середню арифметичну із інтервального ряду, слід для кожного інтервалу знайти його середину і після цього проводити обчислення відомим способом. Розглянемо техніку обчислення на такому прикладі (табл. 3.2.2). Таблиця 3.2.2. Розподіл магазинів за обсягом товарообороту
Насамперед закриємо відкриті інтервали у першій і п’ятій групах магазинів. Закрити інтервали – означає віднайти невідоме мінімальне або максимальне значення ознаки у групі. Закривають інтервали за величиною наступного або попереднього інтервалу. У першій групі відсутнє мінімальне значення ознаки. Величина інтервалу в наступній групі дорівнює 2 млн грн (10–8). Умовно приймається, що і в першій групі величина інтервалу дорівнює 2 млн грн. Тобто мінімальне значення товарообороту в першій групі буде дорівнювати (8–2) 6 млн грн. Отже, перша група включає магазини із товарооборотом від 6 до 8 млн грн. В останній групі відсутнє максимальне значення ознаки. Величина інтервалу в попередній (четвертій) групі дорівнює також 2 млн грн (14–12). Умовно приймається, що і в п’ятій групі магазинів величина інтервалу така ж, як і в попередній. Максимальне значення ознаки в останній групі складатиме 16 млн. грн (14+2). Закривши відкриті інтервали, слід знайти так звану середину інтервалу за середньою арифметичною простою. Так, середина інтервалу в першій групі буде дорівнювати 7 (6+8) : 2, у другій 9 (8+10) : 2 і т. д. Скориставшись формулою середньої арифметичної зваженої, обчислимо середній обсяг товарообороту на один магазин.  млн грн.Звичайно, обчислений середній товарооборот – це досить умовна величина, приблизна. При обчисленні середньої арифметичної замість частот (f), можна брати частості (F – в % до підсумку, або D – коли сума частот приймається за одиницю). Результат від цього не зміниться. Властивість середньої арифметичної. Якщо збільшити або зменшити всі частоти (ваги) в одну і ту саму кількість разів, то числове значення середньої не зміниться. (Розрахунок подано у попередній таблиці). Зменшимо всі частоти у 3 рази: 3:3=1; 9:3=3; 21:3=7 і т. д. Обчислимо середній товарооборот за формулами:  тис. грн.Інші властивості середньої арифметичної та спрощені способи її обчислення Сума відхилень кожного конкретного значення ознаки (х) від середнього значення ознаки (  ) дорівнює нулю. або  .Якщо замість середнього значення ознаки ( ) взяти довільну величину (а) і сума відхилень  не дорівнюватиме "0", то середнє значення можна обчислити за формулою:  , де а – добровільно взята величина; с – середнє відхилення  .Якщо кожну варіанту (х) зменшити або збільшити на величину "а", то й середня зменшиться, або збільшиться на цю величину Якщо кожну варіанту (х) зменшити або збільшити у кілька разів "і", то й середня зменшиться, або збільшиться у стільки ж разів Середня гармонічна У багатьох випадках для обчислення середньої величини використовують середню гармонічну. Середня гармонічна – це величина, обернена середній арифметичній з обернених значень ознаки. Застосовуються у тих випадках, коли відсутні частоти, а є дані про варіанти (х) та добуток варіант на частоти (xf), який для зручності позначимо  w. Проста Зважена   ,де n – число варіант; w– добуток варіант на частоти (xf); 1/x – обернене значення варіанти. Типова задача Протягом години два магазини продавали картоплю по 2,0 та 3,0 грн за кілограм. Одержали однакову виручку по 1200 грн. Визначити середню ціну проданої картоплі. Здавалося б, можна скористатися формулою середньої арифметичної простої  грн. Проте обчислена таким чином середня не буде відповідати дійсності, бо за 1000 кг картоплі, проданих двома магазинами, одержано 2400 грн (1200+1200), а не 2500 (1000 2,5) грн. Середню ціну в такому разі визначають шляхом ділення спільної виручки двох магазинів (2400 грн) на загальну кількість проданої картоплі (1000 кг), обчислену діленням виручки кожного магазину на ціну  .Розв’язок має такий вигляд: 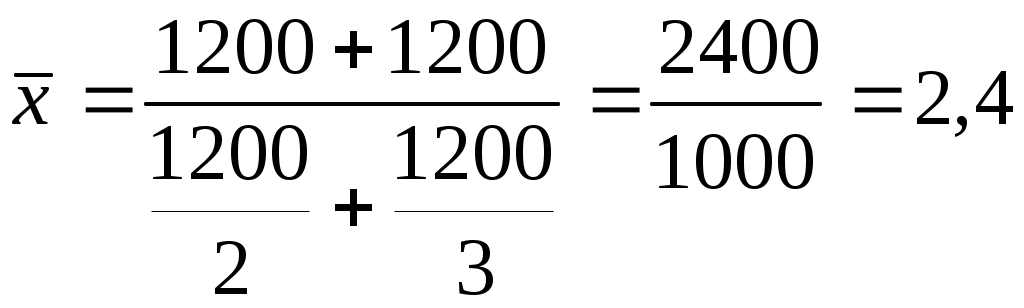 грн. Цей розв’язок можна подати у вигляді формули, де х – ціна одного кілограма картоплі,  – виручка від реалізації продукції.  грн.Це і є формула середньої гармонічної зваженої.  Оскільки виручка від реалізації картоплі в обох магазинах однакова ( 1= 2), цю величину можна винести за дужки у чисельнику і знаменнику і скоротити:  Це і буде формула середньої гармонічної простої. Розв’язок буде мати вигляд:  грн.Залежно від того, які вихідні дані є в умові задачі, використовується відповідний вид середньої: Якщо є варіанти (х) і частоти (f) – використовується середня арифметична зважена. Якщо ж у кожній групі частоти (f) однакові – можна використовувати середню арифметичну просту. Якщо є варіанти (х) і добуток варіанти на частоту (xf =  ) – використовується середня гармонічна зважена.Якщо ж у кожній групі добутки варіанти на частоту (xf = ) однакові, можна використовувати середню гармонічну просту.3.2.6. Середня квадратична Наприклад, потрібно визначити середню сторону квадратів, яка залишила б незмінною їх загальну площу. Припустімо, що сторона першого квадрата дорівнює 20 см, а другого – 30 см (рис. 1).  x1 20 см x2 30 см Рис. 1. Площі і сторони квадратів Визначити середню сторону квадрата. Здавалося б, що для розв’язання задачі найбільш придатна формула середньої арифметичної простої  см.Але ця середня (25 см) дає площу двох рівновеликих квадратів 1250 квадратних сантиметрів  . А реальна площа двох різновеликих квадратів (202+302) становить 1300 квадратних сантиметрів. Отже 25 см – не середня сторона рівновеликих квадратів. Істинна середня сторона рівновеликих квадратів буде дорівнювати кореню квадратному із половини загальної площі двох різновеликих квадратів.  см.На цьому і побудована логіка середньої квадратичної. Середня квадратична, як і всі степеневі середні, буває простою і зваженою: Проста Зважена 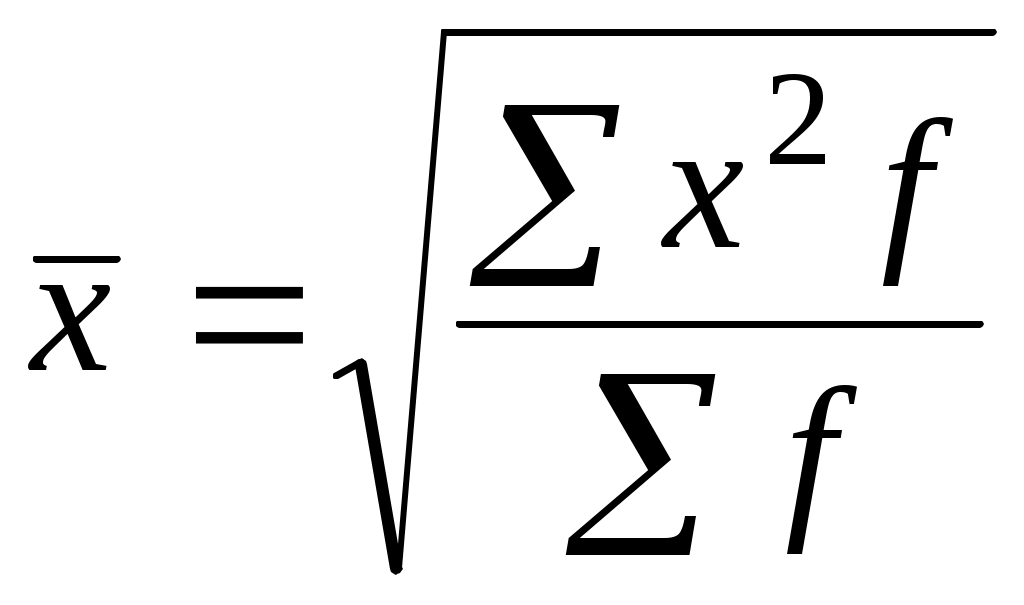  Середня квадратична використовується: При обчисленні середніх сторін квадратів. При обчисленні середніх діаметрів циліндричних тіл (труби, колоди, цистерни, банки, люки, колодязі тощо). В електротехніці при визначенні середніх перерізів провідників електроенергії. У медицині при визначенні середніх діаметрів пухлин, синців, гематом. При обчисленні деяких показників варіації у статистиці (дисперсія, середнє квадратичне відхилення, коефіцієнт варіації). 3.2.7. Середня геометрична Середня геометрична у статистиці (економіці) використовується лише для обчислення середніх коефіцієнтів динаміки, темпів росту та приросту. З’ясуємо поняття середньої геометричної на такому прикладі. Прибуток роздрібного підприємства зріс із 20 до 24 тис. грн у лютому і до 30 тис. грн. у березні, або на 50% .  На скільки процентів в середньому щомісячно зростав прибуток роздрібного підприємства? Здавалося б що на 25%. Якщо за два місяці прибуток зріс на 50%, то в середньому за місяць (50 : 2) – на 25%. Прості розрахунки спростовують це. Якби прибуток щомісячно зростав на 25%, то уже в лютому він досяг би (20 тис. грн + 25%) 25 тис. грн, а в березні (25 тис. грн + 25%) 31,25 тис. грн, а не 30 тис. грн, як задано в умові задачі. Отже в середньому прибуток зростав не на 25%, а на дещо меншу величину. Зробимо обчислення за середньою геометричною. Середня геометрична із п варіант дорівнює кореню п-ної степені із добутку ланцюгових коефіцієнтів динаміки.  , де  – середній коефіцієнт динаміки,  – ланцюгові коефіцієнти динаміки, n– число ланцюгових коефіцієнтів.Підставимо дані задачі у формулу:  Таким чином прибуток роздрібного підприємства в середньому щомісячно зростав у 1,225 раза, або на 22,5%. Перевіримо:  З попередньої теми відомо, що добуток ланцюгових коефіцієнтів динаміки (  ) дорівнює останньому базисному. Звідси формула може мати такий вигляд:  ,  – рівень звітного періоду, – рівень базисного періоду, m– число рівнів ряду динаміки , або календарних дат у періоді.3.2.8. Середня хронологічна Середня хронологічна використовується лише для обчислення середнього рівня моментного ряду динаміки. Припустімо, що нам відома чисельність працівників на початок кожного місяця третього кварталу року (табл. 3.2.4.) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
