статистика заочн.. Практикум київ 2014 Розповсюдження і тиражування без офіційного дозволу кнтеу заборонено
 Скачать 0.97 Mb.
|
Таблиця 4.5Розподіл працівників двох відділів магазину за розміром заробітної плати
Розмах варіаціїРозмах варіації (R) – це різниця між найбільшим і найменшим значенням ознаки.  Відділ А. 2560 – 2360 = 200 грн.Відділ Б. 2480 – 2400 = 80 грн. Він показує, на скільки одиниць максимальне значення ознаки в сукупності відрізняється від мінімального значення. З наведених даних можна зробити висновок, що розмах варіації у відділі А значно вищий. Отже, сукупність у ній менш однорідна, а середня – недостатньо типова. Середнє лінійне відхилення (d) обчислюється без урахування знаків (за модулем) за такими формулами: Просте Зважене  ,де d – середнє відхилення; x– варіанта;  – середнє значення ознаки; n – число варіант; f – частота. Середнє лінійне відхилення показує, на скільки одиниць кожне конкретне значення ознаки (х) в середньому відрізняється від середнього значення ознаки ( ). Обчислимо за даними табл. 4.5. середню заробітну плату працівників першого (А) та другого (Б) відділів:  грн.    грн.Знайдемо відхилення заробітної плати кожного працівника (х) від середньої заробітної плати ( ) у відділах і обчислимо середнє лінійне відхилення (d).  ;  грн.  грн.Висновок.Заробітна плата кожного працівника в середньому відрізняється від середньої заробітної плати в першому відділі на 60 грн, а в другому – на 20 грн. Тобто сукупність працівників другого відділу більш однорідна, а середня, яка її представляє – більш типова. Середній квадрат відхилення (2), або дисперсія обчислюється за формулою: Проста Зважена  У цьому прикладі дисперсія буде дорівнювати у першому відділі  у другому відділі  .Дисперсія – виключно математична величина, яка не має економічного змісту. Середнє квадратичне відхилення – це корінь квадратний з дисперсії. Середнє квадратичне відхилення ( ) Просте Зважене 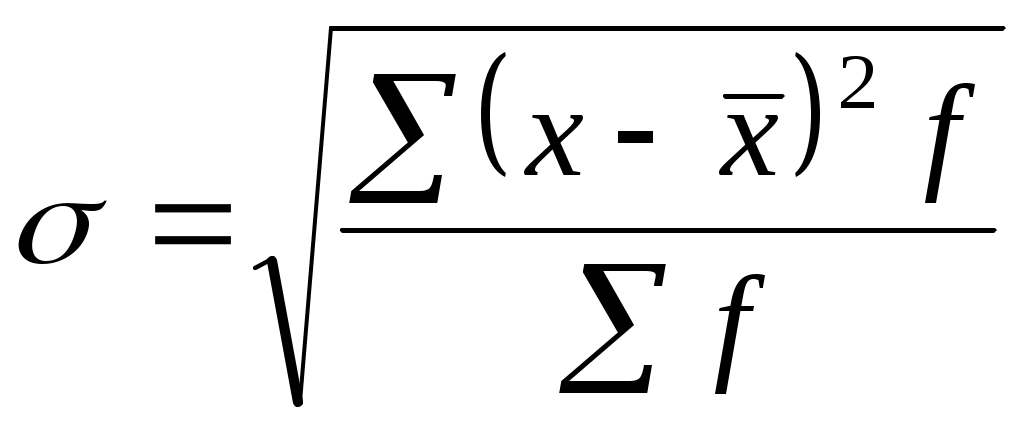  Середнє квадратичне відхилення ( ) показує, на скільки одиниць кожне конкретне значення ознаки (х) в середньому відрізняється від середнього значення ознаки ( ).   грн.  грн.Висновок. Заробітна плата кожного працівника першого відділу відрізняється від середньої заробітної плати в середньому на 70,2 грн, а в другому – на 25,8 грн. Тобто сукупність працівників другого відділу за величиною заробітної плати більш однорідна, ніж в першому, а середня, яка її представляє – більш типова. Середнє квадратичне відхилення () для однієї сукупності завжди більше, ніж середнє лінійне відхилення (d). Так, 1,25d; R : 6 або R : 5. Коефіцієнт варіації показує, на скільки процентів кожне конкретне значення ознаки (х) відрізняється в середньому від середнього значення ознаки ( ).   Висновок.Заробітна плата кожного працівника першого відділу відрізняється від середньої заробітної плати в середньому на 2,9 %, а в другому – на 1,1%. Тобто сукупність працівників другого відділу за величиною заробітної плати більш однорідна, ніж в першому, а середня, яка її представляє – більш типова. Сукупність вважається однорідною, якщо коефіцієнт варіації не перевищує 33 відсотки для нормальних статистичних сукупностей. Отже, сукупність працівників за величиною заробітної плати і в першому, і в другому відділах вважається однорідною, оскільки коефіцієнт варіації (V) у них не перевищує 33 відсотків. 4.3. Спрощені прийоми обчислення середнього квадратичного відхилення Дисперсія, як і середня арифметична, має властивості, знання яких дозволяє обчислювати середнє квадратичне відхилення спрощеним способом. Деякі властивості дисперсіїЯкщо кожне конкретне значення ознаки (х) зменшити або збільшити на будь-яке число (а), то дисперсія від цього не зміниться. Якщо кожне конкретне значення ознаки (х) зменшити або збільшити в одне і теж число разів (і), то дисперсія від цього зменшиться або збільшиться в (і2) разів. Дисперсія ознаки дорівнює різниці між середнім квадратом значень ознаки і квадратом їх середньої. 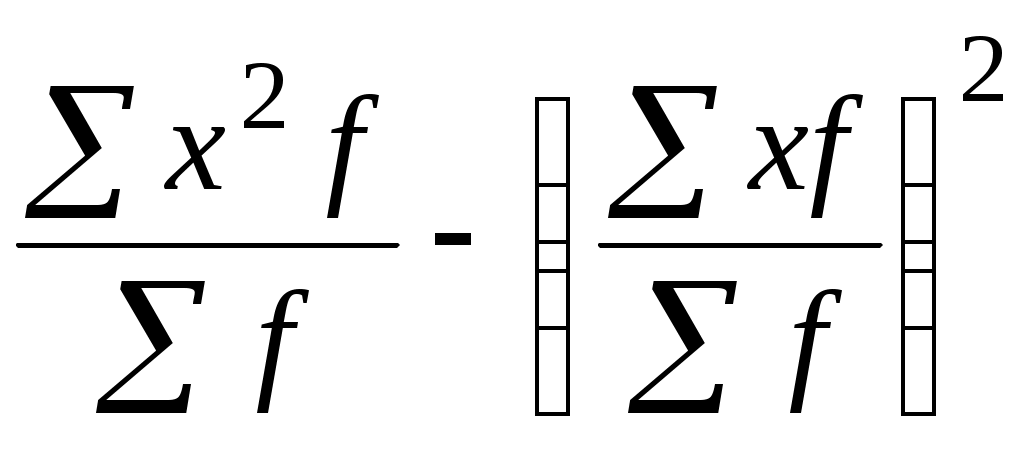 або  Для обчислення усіх показників варіації слід скласти таблицю і зробити в ній відповідні розрахунки (табл. 4.6.). Середня ціна автомобіля обчислюється за формулою середньої арифметичної зваженої  тис. дол.Таблиця 4.6 Робоча таблиця для обчислення основних показників варіації
Розмах варіації =13-3=10 тис. дол. Середнє лінійне відхилення  тис. дол. Дисперсія  Середнє квадратичне відхилення 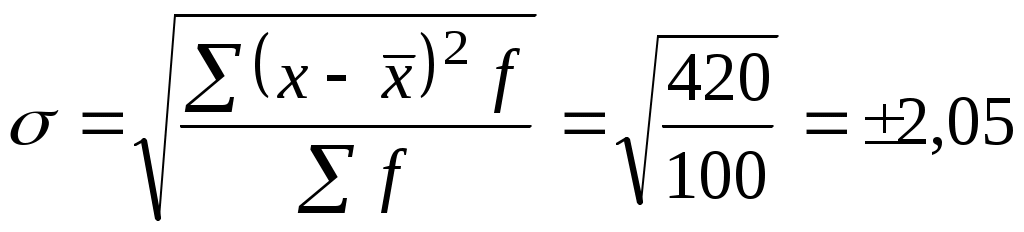 тис. дол. Коефіцієнт варіації  Середнє квадратичне відхилення можна обчислити іншим способом, на основі третьої властивості. 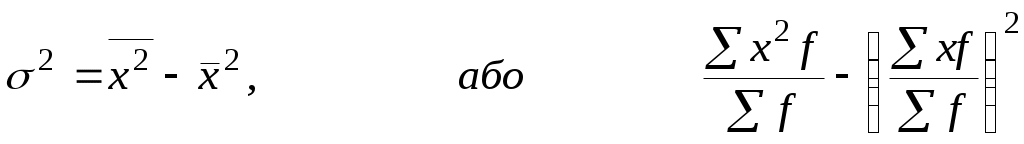 , де  – середній квадрат значень ознаки; – квадрат середнього значення ознаки.Обчислимо дисперсію цим способом на такому прикладі (табл. 4.7). Таблиця 4.7 Робоча таблиця для обчислення дисперсії спрощеним способом
Обчислимо дисперсію ( 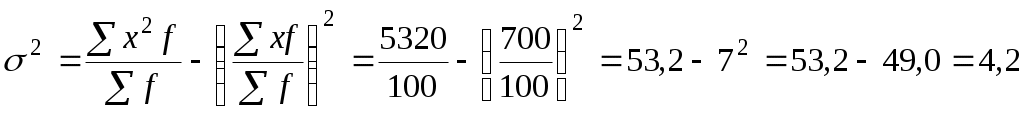 ) спрощеним способом: Середнє квадратичне відхилення (  ) дорівнює кореню квадратному із дисперсії. тис. дол. АНАЛІЗ ТЕНДЕНЦІЙ РОЗВИТКУ 5.1. Поняття про ряди динаміки та їх види Ряд динаміки– це ряд розміщених в хронологічній послідовності статистичних показників для характеристики суспільних явищ. Ряди динаміки поділяють на моментні та інтервальні. Моментним називається ряд динаміки, величини якого характеризують стан явища на певний момент часу. Наприклад, чисельність населення, магазинів, банків, митниць на певну дату. Слід пам’ятати, що показники (рівні) моментних рядів динаміки як правило не підсумовують, оскільки в кожному наступному показнику ряда вміщується попередній або його частина. Разом з тим, з кожної наступної величини моментного ряду динаміки можна віднімати попередню, що дає можливість встановити, як змінився рівень ряду за досліджуваний період. Періодичним (інтервальним) називається ряд динаміки, величини якого характеризують розміри суспільних явищ за певні періоди (інтервали) часу. Наприклад, розмір товарообороту магазинів за рік, виробництво продукції промисловості, сільського господарства, споживання хліба по місяцях (сума дає за рік). Величини інтервального ряду динаміки можна підсумувати. На цій особливості будують ряди накопичених підсумків. 5.2. Показники ряду динаміки, техніка їх обчислення та економічний зміст Кількісні зміни суспільних явищ в часі статистика відображає за допомогою таких показників: рівень ряду динаміки, абсолютний приріст, коефіцієнт динаміки (зростання), темп динаміки (зростання), темп приросту, абсолютне значення одного процента приросту, середні темпи динаміки і приросту, середній абсолютний приріст, коефіцієнт випередження. Рівнями ряду динаміки називають статистичні показники, які характеризують досліджуваний об’єкт. Розрізняють: початковий рівень ряду У0, кінцевий рівень ряду  , середній рівень ряду  .Початковим рівнем називається перший член ряду динаміки (табл. 5.1 – 2600 грн). Кінцевим рівнем називається останній член ряду динаміки (табл. 5.1 – 2680 грн.) Середній рівень періодичного (інтервального) ряду динаміки визначається за формулою середньої арифметичної простої (при рівних проміжках часу між датами (повні ряди динаміки) і за формулою середньої арифметичної зваженої при нерівних проміжках часу (неповні ряди динаміки) (табл. 5.1). Таблиця 5.1 Динаміка середньомісячної заробітної плати трудового колективу
Середньомісячна заробітна плата складатиме:  грн.Середній рівень моментного ряду динаміки визначається за формулами середньої хронологічної простої (для повних рядів динаміки) і середньої хронологічної зваженої (для неповних рядів динаміки), тобто рядів динаміки з нерівними проміжками часу між датами. Рівень, з яким порівнюють, називається базисним (У0), або попереднім (Уп-1). Рівень, який порівнюється, називається поточним або звітним (Уп). Якщо кожний рівень ряду динаміки (Уп) порівнюється з попереднім (Уп-1), то одержані показники називають ланцюговими. Коли ж кожен рівень ряду динаміки (Уп) порівнюється з одним і тим самим рівнем, що є постійною базою порівняння (У0), такі показники називаються базисними. Абсолютним приростом називається різниця між звітним і базисним рівнями. Він показує, на яку величину збільшився або зменшився звітний рівень порівняно з базисним або попереднім періодом часу. Базисний Ланцюговий   , де А– абсолютний приріст; У0 – базисний рівень; Уп– поточний (звітний) рівень; Уп-1 – попередній рівень. За даними табл. 5.2 обчислимо абсолютний приріст і результати внесемо до відповідних граф таблиці. Абсолютний приріст, тис. грн Базисний Ланцюговий  ,  , Лютий =24–20= 4 Лютий =24–20= 4 Березень =30–20= 10 Березень =30–24= 6 . . . . . . . . . . . . . . . . . Травень = 54–20= 34 Травень =54–36= 18 Висновок.У травні порівняно із січнем прибуток фірми збільшився на 34 тис. грн, а порівняно з квітнем – на 18 тис. грн. Між базисними і ланцюговими абсолютними приростами існує зв’язок: сума ланцюгових абсолютних приростів дорівнює останньому базисному.  тис. грн.Різниця між кожним наступним базисним абсолютним приростом і попереднім свідчить про величину відповідного ланцюгового приросту: 34–16=18; 16–10=6; 10–4=6 тис. грн. Коефіцієнт динаміки (зростання) обчислюється як відношення рівня досліджуваного періоду (Уп) до рівня, з яким порівнюють. Показує, у скільки разів рівень звітного періоду збільшився порівняно із базисним або попереднім. Базисний Ланцюговий   Коефіцієнти динаміки прийнято обчислювати із точністю до третього десяткового знаку (0,000). За даними табл. 5.2. обчислимо названі коефіцієнти і внесемо до відповідних граф таблиці. Таблиця 5.2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
=7