Учебно пособие ТБ - 30.05. Практикум Новосибирск 2022 г. Удк ефремов А. М., Транспортная учебное пособие

• Название: Практикум Новосибирск 2022 г. Удк ефремов А. М., Транспортная учебное пособие
• Дата: 28.09.2022
• Размер: 79.27 Kb.
• Имя файла: Учебно пособие ТБ - 30.05.docx
• Тип: Практикум; #702371
• страница: 2 из 7

ПРАКТИЧЕСКАЯ РАБОТА № 2
ПРАКТИЧЕСКОЕ ОПРЕДЕЛЕНИЕ СРЕДНЕГО СРОКА СЛУЖБЫ ЭЛЕМЕНТОВ ПРИЧАЛЬНОГО СООРУЖЕНИЯ

1. Цели работы -

2. Исходные данные

Исходными данными являются статистические (экспериментальные) совокупности, состоящие из n = 20 различных случайных значений X_i – срока службы больверка (год, месяц) (элементов причальной стенки). Результаты наблюдений сводятся в таблицу 1 согласно порядкового номера варианта.

Табл.1.

Результаты измерений Xi год, месяц

X1

X2

X3

X4

X5

……………………..

Xn=20

3. Состав работы:

3.1 Произвести обработку экспериментальных данных (исследовать случайную величину X – срока службы больверка) и объяснить физический смысл результатов.

3.2 Проверить гипотезу о нормальном законе распределения случайной величины X – срока службы больверка по критерию согласия Пирсона.

3.3 В случае подтверждения гипотезы нормального распределения, найти доверительный интервал для истинного значения срока службы больверка.

4. Методические указания

По результатам анализ транспортных проишествий (в работе №1) выяснилось, что основными причинами аварийных случаев на водном транспорте считаются: ошибки судоводительского состава в управлении судном; низкая квалификация членов экипажей судов; износ механизмов и оборудования и т.д., но значительным показателем аварийности на водном транспорте, особенно на внутренних водных путях (ВВП) являются транспортные проишествия связанные с ударами и повреждениями гидротехнических сооружений (ГТС), которые входят в инфраструктуру портов и пристаней – это причальные сооружения. Причальные сооружения являются основными элементами, которые обеспечивают непрерывность, надёжность и безопасность транспортного процесса

Поддержание причальных сооружений в рабочем состоянии являются актуальной для всех портов.

При оценке технического состояния причальных сооружений следует уделять внимание различным видам износа отдельных элементов и сооружения в целом, методам определения качественных и количественных характеристик.

В данной работе предлагается использовать теорию вероятности для определения конкретных сроков службы элементов причальных набережных.

Причальная набережная рассматривается как система, состоящая из строительных конструкций и инженерных устройств, имеющих свой срок службы. При эксплуатации причальных сооружений важно определить значения сроков службы конструктивных элементов, которые вычисляются по натурным данным. Конкретный срок службы конструктивного элемента, выявленный при натуральных исследованиях, рассматривается как случайная величина. Для определения среднего срока службы конструктивного элемента совокупности полученных значений необходимо дать вероятностную оценку.

5. Последовательность выполнения

Составим ряд распределения исследуемой случайной величины X - срока службы

больверка, в годах.

Имеем объем выборки n = 20. Число интервалов разбиения найдем по следующей

формуле: К 1 + 3.21 • lgn. Следовательно, число интервалов разбиения равно К. Найдем длину интервалов 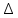. Наибольшее значение срока

службы Х_max = … , а наименьшее X_min = …. Тогда длина интервала вычислится по формуле: =

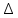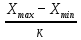
Таким образом, получили К интервалов разбиения:

1-ый интервал [… ; …] - содержит n_i значений исследуемой величины;

2-ой интервал [… ; …] - содержит n_i значения исследуемой величины;

3-ий интервал [… ; …] - содержит n_i значений исследуемой величины;

4-ый интервал [… ; …] - содержит n_i значения исследуемой величины;

5-ый интервал […; …] - содержит n_i значения исследуемой величины.


Ряд распределения исследуемой случайной величины X - срока службы
больверка, в годах сводим в таблицу 2.

Таблица 2.

Интервалы, Года.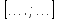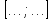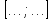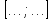
Середины интервалов, х,
Частота, пi
Относитель ная частота,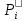

Вычислим точечные оценки неизвестных параметров исследуемой случайной величины X. А именно: М(Х) - математическое ожидание и D(Х) - дисперсия. Напомним, что М(Х) выражает среднее значение случайной величины, которое следует ожидать при испытании, a D(X) характеризует степень рассеяния значений случайной величины около его математического ожидания (выборочная средняя)

М(Х) = ·

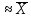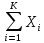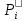
Итак за оценку математического ожидания следует взять число 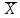, т.е. М(Х) = 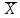года.

Оценим дисперсию D(X). Для этого вычислим выборочную дисперсию 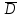и исправленную выборочную дисперсию s².

= ·

= ·

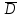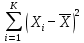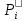
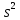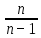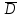
Как доказывает практика, если объем n выборки достаточно "большой" (не менее 30-40
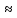
испытаний), то D(X) 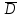, в противном случае D(X) =s².

Таким образом, за оценку дисперсии следует взять D(X) = … год.².

Как известно из курса теории вероятностей, что случайная величина полностью будет
определена, если известен ее закон распределения. Очень часто, исследуемая случайная
величина подчиняется нормальному закону распределения.

Выдвинем гипотезу о нормальном распределении исследуемой случайной величины X -
срока службы больверка. Проверим эту гипотезу с помощью критерия согласия Пирсона.
Как известно, плотность нормального распределения задается формулой:

= · ,

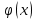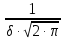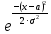где а = М(Х)и 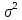= D(X)

Следовательно, у нас два неизвестных параметра a и 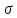. Точечные оценки математического ожидания и дисперсии мы сделали раньше. А именно: а = М(Х) = …, = = …

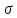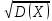Вычислим эмпирические частоты, используя следующую формулу:

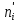=n· ,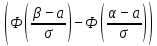

где Ф(х) – функция Лапласа. (1)

a( 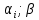) – рассматриваемый интервал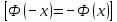

Таблица для эмпирических и теоретических частот выглядит следующим образом:

Таблица 3.

Интервалы	[…; …]	[…; …]	[…; …]	[…; …]	[…; …]
Эмпиричес кие частоты, nt
Теоретичес кие частоты, п[

Эмпирические частоты, n_i берутся из ряда распределения (смотри таблицу 2). Объясним, как вычисляются теоретически е частоты.

Вычислим 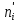по формуле (1).

Вычислим меру отклонения .

= .

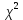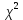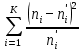Вычислим критическое значение .

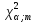Для этого зададим, во-первых, уровень значимости. Допустим а = 0.01.

Вычислим количество степеней свободы т . Формула для вычисления:

m = k – 1 – r,

гдеk— число интервалов;

r - число неизвестных параметров распределения/

Число неизвестных параметров равно 2, так как мы оценивали только а и 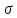, т.е. r = 2.

a = M(X) 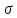= D(X)

Из приложения 2 находим .

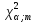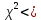
Если 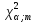, то гипотезу о нормальном распределении срока службы больверка следует принять с заданной вероятностью.

Итак, срок службы больверка есть нормально распределенная случайная величина, что позволяет разрешать различного рода задачи.

Например, можно получить интервальную оценку математического ожидания (ранее была получена точечная оценка а = ….).

Для оценки математического ожидания а случайной величины X, распределенной по нормальному закону, при известной дисперсии D(X) = 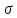² служит доверительный интервал:

- · + · ;

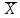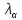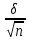
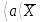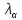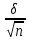где 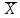= 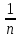· 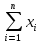– выборочное среднее;
n – объём выборки; 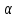- надежность результата;
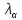- такое значение аргумента функции Лапласа Ф(х), при котором 2 · Ф( 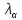) = 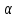. (см. приложение 4)

Если же дисперсия D(X) неизвестна, то для оценки М(Х) = а служит доверительный интервал:

- · + · ,

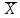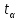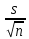
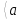
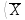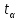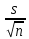где n – объём выборки, (2)

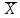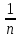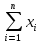₌ · – выборочное среднее,

s = 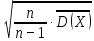= =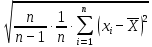 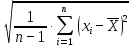- исправленное среднее квадратическое отклонение, a 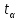- находят по таблице по заданным п и 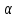(см. приложение 5).

Предположим, мы хотим оценить истинное значение срока службы больверка по данным наших измерений с доверительной вероятностью 1 - 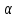= 0.99.

У нас дисперсия D(X) неизвестна, но мы знаем, что срок службы больверка - есть нормально распределенная случайная величина. Поэтому можно воспользоваться 2-ой из приведенных выше формул. Выборочное среднее X и исправленное выборочное отклонение s² были вычислены ранее. X = … иs² = ….

По таблице приложения 5 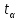= 2.86 при 1 - 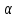= 0.99 и п = 20 .

Следовательно: ·

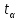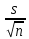
Таким образом, истинное значение срока службы больверка будет лежать в интервале: 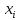— 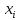< а 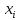< + или x < а < x .

Можно было бы исходить из правила трех сигм, которое гласит, что почти достоверно значения нормально распределенной случайной величины находятся в интервале

(а - 3 · 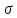; a + 3 · ).

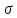В нашем случае а = 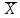и 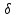или S = 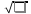. Истинное значение будет лежать в интервале: - 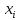< X < .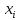

Из всего сказанного, можно сделать вывод, что средний срок службы больверка будет от x_i до x_i лет, но некоторые могут прожить и до x_i лет. Вероятно, замена больверка должна осуществляться до x_i лет, чтобы не было нежелательных последствий. Конечно, чтобы был точнее результат сделанных выводов, нужно делать большую выборку.

6. Контрольные вопросы

6.1 Что такое внутренняя безопасность транспортного процесса?

6.2 Что обеспечивает внутреннюю безопасность?

6.3 Что такое внешняя безопасность?

6.4 Дать определение надёжности?

6.5 Какие методы используются для получения критериев и показателей надёжности?

6.6 Понятие случайная величина (событие)?

6.7 Что такое среднее значение случайной величины?

6.8 Дать определение вероятности безотказной работы?

6.9 Дать определение интенсивности отказов?

6.10 Назначение критерия согласия Пирсона?