|
|
Учебно пособие ТБ - 30.05. Практикум Новосибирск 2022 г. Удк ефремов А. М., Транспортная учебное пособие
ПРАКТИЧЕСКАЯ РАБОТА № 3
ОПРЕДЕЛЕНИЕ ХАРАКТЕРА ФАКТИЧЕСКОГО РАСПРЕДЕЛЕНИЯ ДВИЖЕНИЯ СУДОВ НА ОПАСНЫХ УЧАСТКАХ СУДОВОГО ХОДА
1. Цели работы -
2. Исходные данные
Для наблюдения за интенсивностью движения судов на опасных участках судового хода (створах водного пути) устанавливаются посты, ведущие регистрацию судов и составов. На основании зарегистрированных данных строится таблица и строится гистограмма (Приложение…). Требуется выяснить характер фактического распределения движения судов в створе водного пути за сутки по периодам 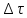 длительностью 0,5 часа при среднем количестве судов М = ?. длительностью 0,5 часа при среднем количестве судов М = ?.
3. Состав работы:
4. Методические указания
В результате выполнения практических работ № 1 и № 2 выяснилось, что основными причинами транспортных проишествий являются:
- судоводительские ошибки (выбор неудачного маневра, ошибки в ориентирование, отсутствие учета внешних факторов, влияющих на управляемость судна, неправильная оценка данных электронавигационных приборов) и др.
Рассмотрим применение теории вероятности применительно к транспортному потоку судов, то есть выясним характер фактического распределения движения судов на опасных участках судового хода, с целью предотвращения аварийных ситуаций.
Транспортный поток судов можно представить как неравномерную во времени последовательность движения неоднородных судовых транспортных средств.
Транспортный поток состоит из различных видов судов: толкачей, буксировщиков-плотоводов, танкеров, грузовых, пассажирских, технических, вспомогательных, на подводных крыльях и воздушной подушке.
Экспериментальная оценка основных характеристик потока судов при многообразии сочетания действующих факторов сложна, а часто и невозможна. В связи с этим основным средством понимания проблемы транспортного потока судов является применение методов моделирования, т.е. создание модели процесса движения потоков судов.
Модель представляет собой идеализированное описание действительного процесса. Она должна как можно точнее характеризовать реальный процесс движения потоков судов, так как невозможно получить полную однозначность с действительным (реальным) процессом движения из-за его большой сложности.
Имеется два метода моделирования: физический и математический.
Физический метод моделирования не может быть полностью использован для изучения транспортного потока и выявления его закономерностей.
Математическое моделирование использует метод описания соотношений между наиболее важными переменными факторами процесса движения потока судов с помощью формул, уравнений, и в большинстве случаев математические модели строятся на определенных гипотезах.
В связи с большим разнообразием факторов, воздействующих на потоки судов, основным способом моделирования является математический. При этом используются детерминистические модели, когда выбранная математическая модель позволяет вычислить изменения одной переменной с изложением других переменных и вероятностные (стохастические) модели, когда в транспортном процессе существуют элементы случайности, а характеристики совокупности системы определяются при помощи анализа отдельных выборок.
Исследования последнего времени на речном транспорте показали, что основные операции флота достаточно хорошо согласуются с законами теории вероятности. Однако применение теории вероятности к решению транспортных задач не гарантирует безопасности плавания, поэтому требуется соблюдать определенную меру при использовании на практике результатов чисто теоретических исследований.
Интенсивность движения - одна из важных характеристик транспортного потока к основная мера сравнения, от которой во многом зависит вероятность аварий. Чем больше судов и составов и чем выше скорость движения, тем чаще возникает необходимость в расхождениях и обгонах, тем больше вероятность в неправильных и несогласованных действиях судоводителей.
Простейшей математической моделью, описывающей поток судов, является динамическая модель, используемая для определения возможной интенсивности движения на одной полосе судового хода:
M = 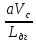 , суд/ч (1) , суд/ч (1)
где a — коэффициент размерности; Vc— скорость движения судов в потоке, км/ч; 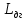 — динамический габарит, т.е. расстояние между судами, следующими друг за другом, м. — динамический габарит, т.е. расстояние между судами, следующими друг за другом, м.
Данная математическая модель принята при ряде допущений: скорость всех судов в потоке одинакова, суда однотипны, имеют одинаковые габариты и тормозные характеристики.
Динамический габарит определяется по формуле:
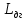 = = 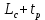 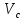 + + 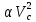 (2) (2)
где 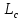 — длина судна, м; — длина судна, м; 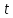 p — время реакции судоводителя, мин; p — время реакции судоводителя, мин; 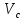 — скорость судна, м/мин; — скорость судна, м/мин; 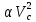 — величина пути торможения судна, м; — величина пути торможения судна, м; 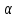 — коэффициент размерности. — коэффициент размерности.
Уравнение (2) является квадратичной функцией, интенсивность имеет предел при определенном значении скорости потока, а в целом формула (2) больше соответствует требованиям обеспечения безопасности движения судов с высокими скоростями.
В случае если поток судов плотный, а скорости движения небольшие, действительная дистанция между движущимися судами может быть меньше их тормозных путей. Следовательно, динамический габарит необходимо определять с учетом возможной разницы тормозных путей судов.
Интенсивность движения судов на внутренних водных путях отличается большой изменчивостью, поэтому для ее изучения необходимо применять методы теории вероятности и математической статистики. При малой и средней интенсивности движения судов транспортный поток приближенно можно считать простейшим потоком событий.
Для описания транспортного потока речных судов при допущении отсутствия их взаимного влияния вполне приемлемо использование закона распределения редких событий или закона Пуассона.
Закон Пуассона независимо от вероятности события имеет место тогда, когда эти события распределяются с одинаковой средней плотностью независимо друг от друга и совместное наступление двух или нескольких событий практически исключено. Закон Пуассона выражается
Pk = 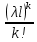 · · 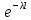 (3) (3)
где 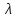 — средняя плотность потока событий; — средняя плотность потока событий; 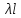 — среднее число событий, наблюдаемых на отрезке длиной l; k — число событий. — среднее число событий, наблюдаемых на отрезке длиной l; k — число событий.
Дисперсия случайной величины, распределенной по закону Пуассона, равна ее математическому ожиданию 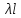 . Таким образом, если математическое ожидание или среднее число событий, наблюдаемое на некотором промежутке (принятом за единицу), равно . Таким образом, если математическое ожидание или среднее число событий, наблюдаемое на некотором промежутке (принятом за единицу), равно 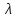 , то вероятность того, что на интервале l произойдет ровно kсобытий, определяется законом распределения Пуассона. , то вероятность того, что на интервале l произойдет ровно kсобытий, определяется законом распределения Пуассона.
Этот закон достаточно хорошо подходит к условиям свободного движения судов по внутренним водным путям.
Математическое выражение закона редких событий применительно к нашим условиям будет иметь вид:
Px = 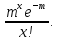 (4) (4)
где Рx - вероятность прохода одного или нескольких судов в определенном створе водного пути за промежуток времени t; m— среднее число проходящих судов: х — число судов (при х = 0 непоявление судна).
Для наблюдения за интенсивностью в заданных створах водного пути устанавливаются посты, ведущие регистрацию судов и составов. На основании зарегистрированных данных составляются таблицы и строятся гистограммы.
Для оценки точности теоретического описания вероятностного процесса в сравнении с действительным использованием критерий Пирсона 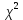 , формула которого имеет вид: , формула которого имеет вид:
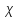 2 = 2 = 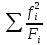 – n. (5) – n. (5)
где fi- наблюдаемая частота случаев; Fi – теоретическая частота случаев; n – общее число случаев.
Величина интервалов времени между движущимися друг за другом судами (т.е. длины промежутков между соседними событиями) является важной характеристикой транспортного потока судов.
Распределение интервалов между проходящими створ судами - непрерывно меняющиеся процессы, которые также могут быть определены с помощью закона распределения редких событий.
Проведенные исследования позволяют сделать вывод, что для описания транспортного потока судов на внутренних водных путях вполне применим закон распределения редких событий. Однако практическое распределение иногда не совпадает с распределением Пуассона. Значительные расхождения бывают в областях средних и больших интервалов, так как по допущению отсутствует взаимное влияние судов, хотя уже при небольшой интенсивности возникают помехи движению.
Отклонения от закона распределения редких событий при практическом движении будут проявляться: в большей мере при значительной разнородности состава транспортного потока судов; при больших размерах и плотности потока, ограничивающего свободу движения; при большом количестве затруднительных участков, создающих помехи движению; при большом числе задержек, например, у шлюзов, мостов и др.
Скорость движения имеет большое значение для безопасности плавания. Чем значительнее разница в скоростях движения судов и составов в транспортном потоке, тем чаще возникает потребность в обгонах, а это приводит к повышению возможности аварийных происшествий.
Количество аварийных случаев возрастает с увеличением скорости судов. Поэтому снижение скорости движения - определенная мера, обеспечивающая безопасность плавания. Однако это входит в крупное противоречие с общей задачей увеличения скорости движения судов, сокращения сроков доставки грузов и увеличения экономической эффективности работы судов.
Выработать конкретные рекомендации режимов скоростей движения судов на все случаи невозможно. Скорость всегда должна соответствовать конкретно сложившейся обстановке. Каждый судоводитель при выборе скорости должен учитывать все условия, влияющие на безопасность плавания, и в зависимости от этих условий выбирать безопасную скорость движения. В связи с этим в Правилах плавания уделяется значительное внимание обеспечению безопасной скорости движения судна.
5. Последовательность выполнения
5.1 Строится гистограмма (Приложение…)
5.2 Расшифровать гистограмму и перенести данные в таблицу 1.
Таблица 1.
x
|
0
|
1
|
…
|
…
|
…
|
xi
|
|
nx
|
|
|
|
|
|
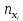
|
|
x – число судов;
nx– количество интервалов 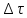 длительностью 0,5 ч. длительностью 0,5 ч.
Как известно фактическое распределение движения судов (интенсивности) описывается в виде закона редких событий (см. теорию, формула 4), т.е. определяется законом распределения Пуассона.
Применительно к нашим условиям будет иметь вид:
P(x) = 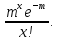 (1) (1)
где P(x) – вероятность прохода x судов в определённом створе водного пути за промежуток времени 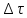 ; ;
m – среднее число прохода судов;
x – число судов;
x! - факториал натуральных чисел.
Применительно к рассматриваемой задаче:
x - число судов, проходящих за период 0,5 часа;
fx = n – наблюдаемая частота движения;
P(x) – теоретическая вероятность прохождения;
Fx = pP(x) – расчётная частота движения (2)
(p =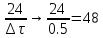
m = 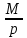 . (3) . (3)
5.3 Вычисляем теоретические вероятности прохождения (формула 1);
5.4 Вычисляем расчётные частоты движения (формула 2);
5.5 Полученные результаты заносим в таблицу 2.
Таблица 2.
x
|
P(x)
|
F(x)=nx
|
Fx
|
.
.
.
.
.
xn
|
.
.
.
.
.
Pi(x)
|
.
.
.
.
.
.
|
|
|
|
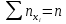
|
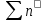
|
На основании результатов таблицы 2 провести анализ согласования расчётных и натуральных наблюдений (частот), если отношения незначительные, то для оценки точности теоретического описания можно воспользоваться критерием Пирсона
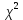 = = 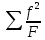 – n (4) – n (4)
За меру отклонения наблюдаемых данных от расчётных применяется сумма квадратов отклонений частностей от теоретической вероятности показания отдельного значения.
Расчётные значения 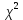 сравниваем с табличным (приложение 4) сравниваем с табличным (приложение 4)
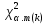
где 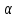 = 0,05 или 95% - уровень значимости, = 0,05 или 95% - уровень значимости,
а m(k) – число степеней свободы.
Число степеней свободы расчитывается следующим образом:
K = S – r – 1.
где S – количество интервалов;
r – число параметров предполагаемого распределения.
В нашем случае предполагаемое распределение определяется только одним параметром m(формула 1), тогда r = 1; а количество интервалов см. таб. 2
Если 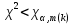 , тогда фактическое распределение действительно согласуется с теоретическим, необходимо сделать выводы в заключении. , тогда фактическое распределение действительно согласуется с теоретическим, необходимо сделать выводы в заключении.
Если 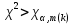 , необходимо проанализировать работу, выделить величины которые влияют на данное условие и предложить рекомендации для безопасного прохождения опасных участков судового хода. , необходимо проанализировать работу, выделить величины которые влияют на данное условие и предложить рекомендации для безопасного прохождения опасных участков судового хода.
6. Контрольные вопросы
6.1 Какие мероприятия обеспечивают безопасность плавания?
6.2 Что такое транспортный поток?
6.3 Какие существуют методы моделирования транспортного потока?
6.4 Цель математического моделирования потока движения судов?
6.5 Объяснить понятие – интенсивность движения судов в потоке?
6.7 Объяснить простейшую математическую модель для определения интенсивности движения судов?
6.8 В каких случаях возможно значительное отклонение результатов теоретических и практических данных при использовании закона редких событий?
6.9 Что такое гистограмма?
6.10 Скоростной режим и его влияние на безопасность транспортного потока?
|
|
|
 Скачать 79.27 Kb.
Скачать 79.27 Kb.
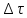 длительностью 0,5 ч.
длительностью 0,5 ч.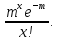 (1)
(1)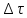 ;
;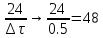
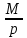 . (3)
. (3) 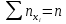
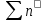
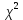 =
= 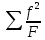 – n (4)
– n (4)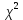 сравниваем с табличным (приложение 4)
сравниваем с табличным (приложение 4)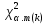
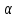 = 0,05 или 95% - уровень значимости,
= 0,05 или 95% - уровень значимости, 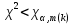 , тогда фактическое распределение действительно согласуется с теоретическим, необходимо сделать выводы в заключении.
, тогда фактическое распределение действительно согласуется с теоретическим, необходимо сделать выводы в заключении.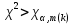 , необходимо проанализировать работу, выделить величины которые влияют на данное условие и предложить рекомендации для безопасного прохождения опасных участков судового хода.
, необходимо проанализировать работу, выделить величины которые влияют на данное условие и предложить рекомендации для безопасного прохождения опасных участков судового хода.
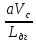 , суд/ч (1)
, суд/ч (1)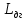 — динамический габарит, т.е. расстояние между судами, следующими друг за другом, м.
— динамический габарит, т.е. расстояние между судами, следующими друг за другом, м.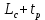
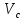 +
+ 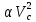 (2)
(2)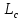 — длина судна, м;
— длина судна, м; 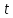 p — время реакции судоводителя, мин;
p — время реакции судоводителя, мин; 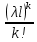 ·
· 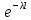 (3)
(3)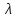 — средняя плотность потока событий;
— средняя плотность потока событий; 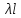 — среднее число событий, наблюдаемых на отрезке длиной l; k — число событий.
— среднее число событий, наблюдаемых на отрезке длиной l; k — число событий.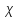 2 =
2 = 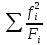 – n. (5)
– n. (5)