ЛАБОРАТОРНЫЙ ПРАКТИКУМ ПО ХИМ ТЕРМОДИНамиКЕ. Практикум по химической термодинамике учебное пособие для студентов всех специальностей

• Название: Практикум по химической термодинамике учебное пособие для студентов всех специальностей
• Анкор: ЛАБОРАТОРНЫЙ ПРАКТИКУМ ПО ХИМ ТЕРМОДИНамиКЕ.doc
• Дата: 19.05.2017
• Размер: 2.28 Mb.
• Имя файла: ЛАБОРАТОРНЫЙ ПРАКТИКУМ ПО ХИМ ТЕРМОДИНамиКЕ.doc
• Тип: Практикум; #7896
• страница: 10 из 15

Трехкомпонентные системы
Для трехкомпонентной системы, на равновесие которой из внешних факторов оказывают влияние только давление и температура – правило фаз Гиббса –выражается уравнением

С = 5 – Ф.

(3.18)

Отсюда следует, что в трехкомпонентной системе число фаз, находящихся в равновесии, не может быть более пяти (С = 0, если Ф = 5), а максимальное число термодинамических степеней свободы, т.е. независимых параметров состояния системы, равно четырем – давление, температура, концентрации Х₁ и Х₂ двух компонентов, выраженные в массовых или молярных долях или процентах (С = 4, если Ф = 1). При выбранных параметрах состояния системы (Р, Т, Х₁, Х₂) полная диаграмма состояния должна быть четырехмерной. В связи с этим состояние трехкомпонентной системы и равновесие фаз в ней рассматривают при постоянном давлении и строят трехмерную пространственную диаграмму состояния в виде прямой трехгранной призмы, основанием которой служит равносторонний треугольник состава, а по высоте откладывается температура. При Р = const

Сусл = 4 – Ф.

(3.19)

Изучение равновесий в трехкомпонентной системе еще более упрощается при постоянных давлении и температуре. В этом случае, можно использовать плоскую диаграмму состояния, являющуюся сечением трехгранной призмы, параллельным основанию (диаграмма состава). При Р = const и Т = const

Сусл = 3 – Ф.

(3.20)

Для графического изображения состава трехкомпонентных систем при постоянных Р и Т применяются треугольные и прямоугольные диаграммы. Треугольные диаграммы строят по методу Гиббса или по методу Розебома. В каждом из этих методов используется равносторонний треугольник, вершины которого соответствуют чистым компонентам А, В и С (рис. 3.15).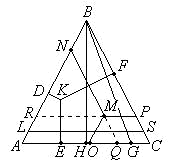



Рис. 3.15. Изображение состава трехкомпонентной системы

Фигуративная точка, лежащая на любой из сторон треугольника, изображает состав соответствующей двухкомпонентной системы, а фигуративная точка, находящаяся внутри этого треугольника, – состав трехкомпонентной системы. При анализе треугольных диаграмм используют свойства равностороннего треугольника:

1) сумма длин перпендикуляров, опущенных из любой точки, лежащей внутри равностороннего треугольника, на его стороны, есть величина постоянная, равная высоте этого треугольника (KD + КЕ + KF = ВН);

2) сумма отрезков прямых, проведенных параллельно сторонам равностороннего треугольника через любую точку, лежащую внутри этого треугольника, есть величина постоянная, равная стороне треугольника (MN + МО + МР = АВ = ВС = АС).

Из этих свойств следует:

а)точки,лежащие на прямой(LS), параллельной одной из сторон равностороннего треугольника (АС), противолежащей данной вершине (В), изображают составы системы с постоянным содержанием того компонента, которому соответствует эта вершина (В);

б) точки, лежащие на прямой (BG), проходящей через вершину треугольника (В), изображают составы системы с постоянным соотношением концентраций двух других компонентов (А и С).

Метод Гиббса основан на использовании первого свойстваравностороннего треугольника. Для удобства изображения состава трехкомпонентной системы по методу Гиббса каждую высоту треугольника делят на 100 (или 10) равных частей и через точки деления проводят прямые, параллельные сторонам треугольника. Длина каждой полученной части будет соответствовать 1 % (или 10 %). Чтобы по методу Гиббса указать состав трехкомпонентной системы, изображенной на диаграмме фигуративной точкой К (рис. 14), из точки К опускают перпендикуляры на стороны треугольника. Длина каждого перпендикуляра будет отвечать содержанию одного из компонентов: процентное содержание компонента А характеризуется отрезком KF, компонента В – отрезком КЕ и компонента С – отрезком KD.

Метод Розебома основан на использовании второго свойстваравностороннего треугольника. Для удобства изображения состава трехкомпонентной системы по методу Розебома каждую сторону треугольника делят на 100 (или 10) равных частей и через точки деления проводят прямые, параллельные сторонам треугольника. Длина каждой части соответствует 1 % (или 10 %). Для того чтобы по методу Розебома указать состав трехкомпонентной системы, изображенной на диаграмме фигуративной точкой М (рис. 14), из точки М проводят прямые, параллельные сторонам треугольника. Содержание компонента А характеризуется отрезком МР, компонента В –отрезком МО и компонента С –отрезком МN.

Состав трехкомпонентной системы можно также изобразить с помощью прямоугольной диаграммы. Этот способ выражения состава трехкомпонентной системы широко используется при изучении равновесий в растворах солей, имеющих низкую растворимость. Начало координат прямоугольной диаграммы соответствует воде, а концентрации двух солей, наносятся на оси абсцисс и ординат. Этот способ изображения состава значительно проще метода Розебома, но его недостаток в том, что фигуративные точки солей находятся в бесконечности.