ЛАБОРАТОРНЫЙ ПРАКТИКУМ ПО ХИМ ТЕРМОДИНамиКЕ. Практикум по химической термодинамике учебное пособие для студентов всех специальностей
 Скачать 2.28 Mb. Скачать 2.28 Mb.
|
1. ТЕПЛОВЫЕ ЭФФЕКТЫ ХИМИЧЕСКИХ РЕАКЦИЙИ КАЛОРИМЕТРИЯ1.1. ТЕОРЕТИЧЕСКАЯ ЧАСТЬОсновные понятия Термодинамика изучает взаимные переходы различных форм энергии, не ограничиваясь рассмотрением соотношений между теплотой и механической работой. Термодинамика основана на трех законах природы, благодаря этому ее выводы обладают общностью и не зависят от статистической теории, как классической, так и квантовой. Объектом изучения термодинамики является система. Формально система определяется как некоторая часть объективного мира, которая подвергается термодинамическому изучению. Термохимия – раздел химической термодинамики, в задачу которой входит определение и изучение тепловых эффектов реакций, а также установление их взаимосвязей с различными физико-химическими параметрами. Ещё одной из задач термохимии является измерение теплоёмкостей веществ и установление их теплот фазовых переходов. Первый закон термодинамики Первый закон термодинамики это закон сохранения энергии. «Энергия мира остается постоянной» (Клаузиус). Поэтому если некоторая система теряет энергию, то в окружающей среде должно наблюдаться соответствующее увеличение ее. Кроме того, когда энергия одного вида превращается в энергию другого вида, должно существовать количественное соотношение между этими величинами, независимое от систем и определяемое только формами превращающейся энергии. Чтобы выразить первый закон в математическом виде, рассмотрим некоторую систему, содержащую определенное количество вещества – твердого, жидкого или газообразного. Система может быть гомогенной или гетерогенной и подвергаться или не подвергаться химическому изменению. С изменением состояния системы в общем связаны следующие изменения энергии:
где Q и А - неполные дифференциалы. Работа A может складываться из работ различного типа: механической, электрической, гравитационной и поверхностной. Ограничимся только механической работой. Если система под давлением Р увеличивает свой объем на бесконечно малую величину dV, то работа, совершенная системой над окружающей средой , равна PdV. Поэтому для любого изменения в системе с постоянной массой при отсутствии электрического, гравитационного и поверхностного изменений A = PdV и первый закон записывается в виде:
где U – внутренняя энергия системы. Второй закон термодинамики В отличие от первого закона термодинамики, применимого ко всем явлениям, второй закон применим только к обратимым процессам. Это закон гласит, что если количество тепла Q поглощается путем обратимого процесса при температуре T, то энтропия системы возрастает на величину
Обратимым называется такой процесс, при котором система во всех стадиях процесса лишь бесконечно мало отклоняется от состояния равновесия. Примерами обратимых процессов могут служить процессы плавления твердых тел, растворения солей и испарения жидкостей при равновесных условиях. Однако, повседневный опыт показывает, что все естественные и самопроизвольные процессы протекают необратимо. Возрастание энтропии системы, подвергающейся необратимому изменению, больше величины Q/T. При изложении термодинамики с применением методов статистической теории мерой вероятности состояния системы (неупорядоченности системы) является энтропия S – величина, пропорциональная логарифму числа равновероятных микросостояний, которыми может быть реализовано данное макросостояние, характеризующееся макроскопическими свойствами системы (температура, давление, объем и т.п.):
где k = 1,38∙10-23 (Дж/моль∙К) – постоянная Больцмана; W – термодинамическая вероятность, т.е. число возможных микросостояний системы, осуществляющее данное макросостояние. Чем больше неупорядоченность, тем больше энтропия и наоборот. Энтропию относят к 1 моль вещества, и она имеет размерность Дж/(моль·К). Для большинства веществ определены и сведены в таблицы термодинамических констант стандартные значения (Р = 1,013·105 Па) энтропии S0298, полученные при 25С. Далее S0298, будут обозначаться просто S0, с указанием вещества, к которому они относятся. Например, S0(O2) = 205,0 Дж/(моль·К); S0(CO2) = 213,8 Дж/(моль·К). Пример 1. Предскажите знак изменения энтропии ΔS0х.р. в приведенных реакциях:
Решение 1) ΔS0х.р. > 0, так как в результате реакции образуется газообразный кислород, а исходное вещество было кристаллическим, т.е. не упорядоченность в системе возрастает. 2) ΔS0х.р. < 0, так как в реакцию вступает 3 моль газов, а образуются 2, т.е. число частиц газообразных веществ уменьшается, в системе растет упорядоченность. Третий закон термодинамики При стремлении температуры к нулю кельвин энтропия любого вещества в изотермических процессах (T = const) перестает зависеть от каких-либо его параметров и в пределе стремиться к одной величине, которую принимают за ноль:
Данная формулировка третьего закона термодинамики принадлежит Планку. Из нее следует, что изменение энтропии для кристаллических веществ при всех изотермических процессах, происходящих при абсолютном нуле, также равно нулю. Третий закон термодинамики устанавливает ноль отсчета энтропии, поэтому энтропию вещества можно измерять в абсолютных единицах. Первый и второй законы термодинамики оперируют с изменениями энергии и энтропии, третий закон – с их абсолютными значениями. Ни одна система не может обладать отрицательной энтропией. Система, обладающая нулевой энтропией, является наиболее упорядоченной, с возрастанием энтропии системы возрастет ее разупорядоченность. ЭНЕРГЕТИКА ХИМИЧЕСКИХ РЕАКЦИЙ Тепловые эффекты химических реакций Количество теплоты. Уравнение теплового баланса Количество теплоты – это количественная мера изменения внутренней энергии тела при теплообмене. Единица измерения – джоуль (Дж). Количество теплоты при нагревании или охлаждении можно рассчитать по формуле:
где Q – количество теплоты; сm – мольная теплоемкость вещества Дж/(К·моль) или кал/(моль∙град); Коэффициент пропорциональности между количеством сообщенной телу теплоты и изменением его температуры называется теплоемкостью: Q = С∙ΔТ; С = Q/ΔТ. Мольной теплоемкостью cm называется количество тепла, которое необходимо сообщить одному молю вещества для того, чтобы увеличить его температуру на один градус Кельвина. Удельной теплоемкостью называется количество тепла, необходимое для увеличения температуры одного килограмма вещества на один градус Кельвина. При нагревании тело получает энергию; при охлаждении – выделяет, так как T = T1 – T2 < 0, Q < 0. Если теплообмен происходит между несколькими телами, составляющими изолированную от окружающих тел систему, то применяют уравнение теплового баланса:
где Q1, Q2, Q3 – количество теплоты, полученное или отданное телами; n – число тел, участвующих в теплообмене. Теплоту, полученную телом, считают положительной и в уравнении ставят знак «+»; теплоту, отданную телом, считают отрицательной и ставят знак «-». Тепловым эффектом химической реакции называют алгебраическую сумму поглощенной при реакции теплоты и совершённой работы за вычетом работы против сил внешнего давления (pΔV). В соответствии с первым законом термодинамики:
где ΔU – изменение внутренней энергии системы; A – совершенная системой работа. Тепловой эффект реакции зависит от пути и способа проведения процесса. Однако, по крайней мере, при соблюдении одного из двух условий теплота химической реакции не зависит от пути и способа осуществления взаимодействия:
где U2 – внутренняя энергия продуктов реакции; U1 – внутренняя энергия исходных веществ;
где Н2 – энтальпия продуктов реакции; Н1 – энтальпия исходных веществ. Измерение тепловых эффектов реакций составляет обширную область термохимии, данные которой позволяют составить правильное представление об энергетической ценности той или иной реакции, ее внутреннем механизме, возможном направлении кинетики и т.д. Для практических измерений тепловых эффектов употребляются калориметры. Результаты термохимических измерений – тепловые эффекты реакций – принято относить к одному молю образующегося вещества. Количество теплоты, которое выделяется при образовании 1 моля соединения из простых веществ, называется теплотой образования данного соединения. Например, выражение «теплота образования воды равна 285,8 кДж/моль» означает, что при образовании 18 г жидкой воды из 2 г водорода и 16 г кислорода выделяется 285,8 кДж. Если элемент может существовать в виде нескольких простых веществ, то при расчете теплоты образования этот элемент берется в виде того простого вещества, которое при данных условиях наиболее устойчиво. Теплоты образования наиболее устойчивых простых веществ принимаются равными нулю. Например, при обычных условиях наиболее устойчивой формой кислорода является молекулярный кислород О2, теплота образования которого считается равной нулю. Теплота же образования озона О3 равна -142 кДж/моль, поскольку при образовании из молекулярного кислорода одного моля озона поглощается 142 кДж. Тепловые эффекты можно включать в уравнения реакций. Химические уравнения, в которых указано количество выделяющейся или поглощаемой теплоты, называются термохимическими уравнениями. Величина теплового эффекта указывается обычно в правой части уравнения со знаком «+» в случае экзотермической реакции и со знаком «-» в случае эндотермической реакции. Например, термохимическое уравнение реакции образования жидкой воды имеет вид 2H2 + O2 = 2H2O +571,6 кДж или H2 + ½O2 = H2O +285,8 кДж. Возможна и другая запись термохимических уравнений, в которой величина теплового эффекта указана в виде изменения энтальпии ∆H. Часто изменение энтальпии записывается как ∆H0298. Верхний индекс 0 означает стандартную величину теплового эффекта реакции, а нижний температуру, при которой идет взаимодействие. В реакциях, идущих с выделением теплоты (экзотермических), энтальпия системы уменьшается (∆H < 0); в реакциях, идущих с поглощением теплоты (эндотермических), энтальпия системы увеличивается (∆H > 0). Ниже приведен пример записи термохимического уравнения с учетом вышесказанного: N2 + O2 = 2NO, ∆H0298 = +90,25 кДж. Данная запись означает, что реакция образования оксида азота (II) идет с поглощением теплоты (эндотермическая). Обе формы записи правильны и возможно использование любой из них. Важнейшей характеристикой веществ, применяемых в качестве топлива, является их теплота сгорания. Эту величину также принято относить к одному молю вещества. Таким образом, выражение «теплота сгорания ацетилена равна 1300 кДж/моль» эквивалентно термохимическому уравнению С2H2 + 2½O2 = H2O + 2CO2 + 1300 кДж. Величина теплового эффекта зависит от природы исходных веществ и продуктов реакции, их агрегатного состояния и температуры. Для удобства сравнения различных реакций по величинам их тепловых эффектов последние обычно указывают для случая, когда температура исходных веществ и продуктов реакции равна 250С1. При этом также подразумевается, что участвующие в реакции вещества находятся в том агрегатном состоянии, которое устойчиво при 250С (стандартной температуре). Агрегатное состояние вещества указывается в уравнении реакции: для обозначения кристаллического состояния используется знак (к) около формулы вещества, жидкого – (ж), газообразного – (г). Изменение давления, концентрации веществ и температуры приводит к смещению равновесия в ту или иную сторону. Направление смещения определяется известным принципом Ле-Шателье: при воздействии на систему, находящуюся в равновесии, равновесие смещается в сторону той из двух противоположных реакций (прямой или обратной), которая ослабляет эффект внешнего воздействия. Остановимся подробнее на влиянии температуры. Реакция между кислородом и водородом сопровождается выделением тепла (уменьшением энтальпии) 2Н2 + О2 = 2Н2О + Q (H0). Пусть все три вещества при температуре Т1 находятся в равновесии, описываемом константой К1: 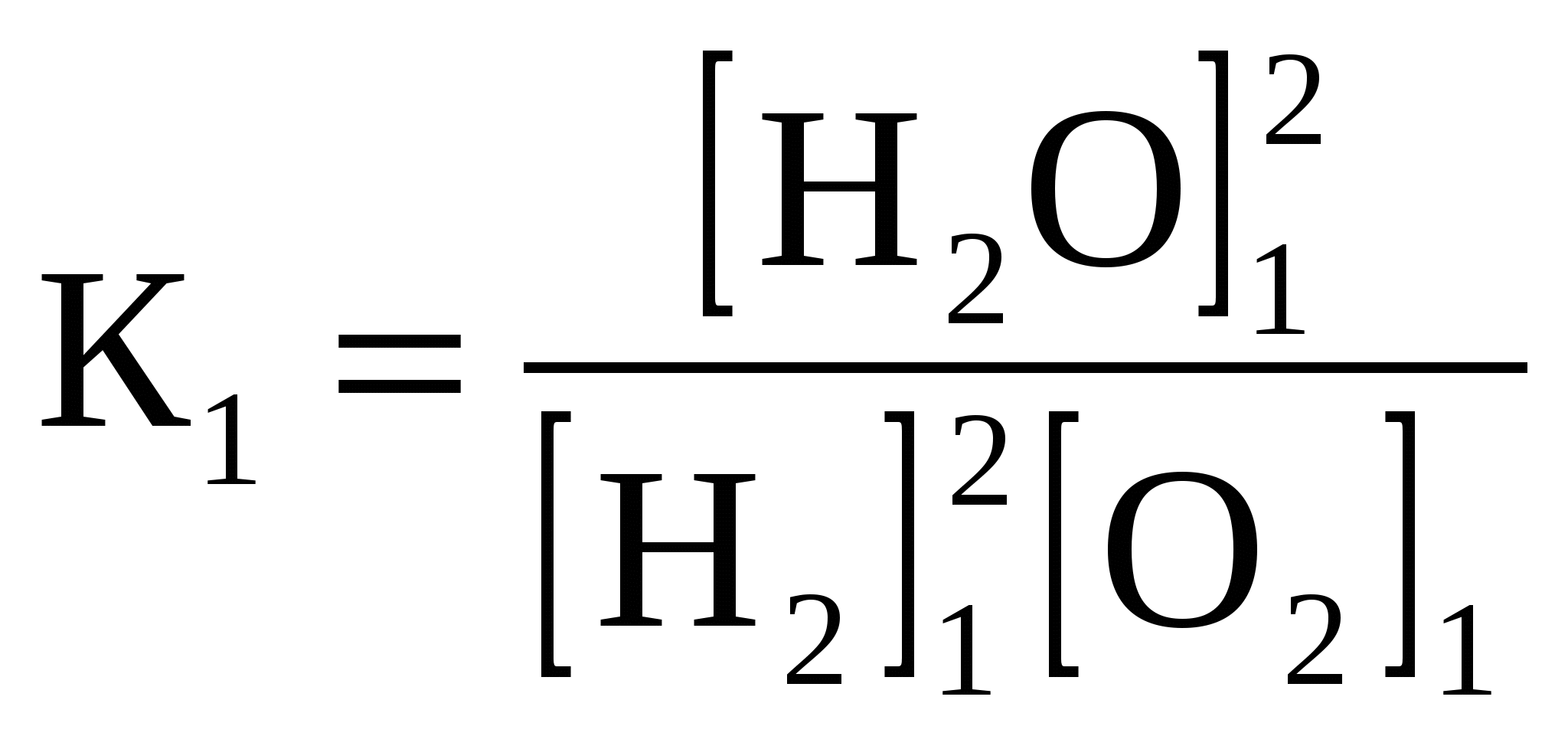 . .Затем температура повышается до Т2 и достигнуто новое состояние равновесия с константой К2: 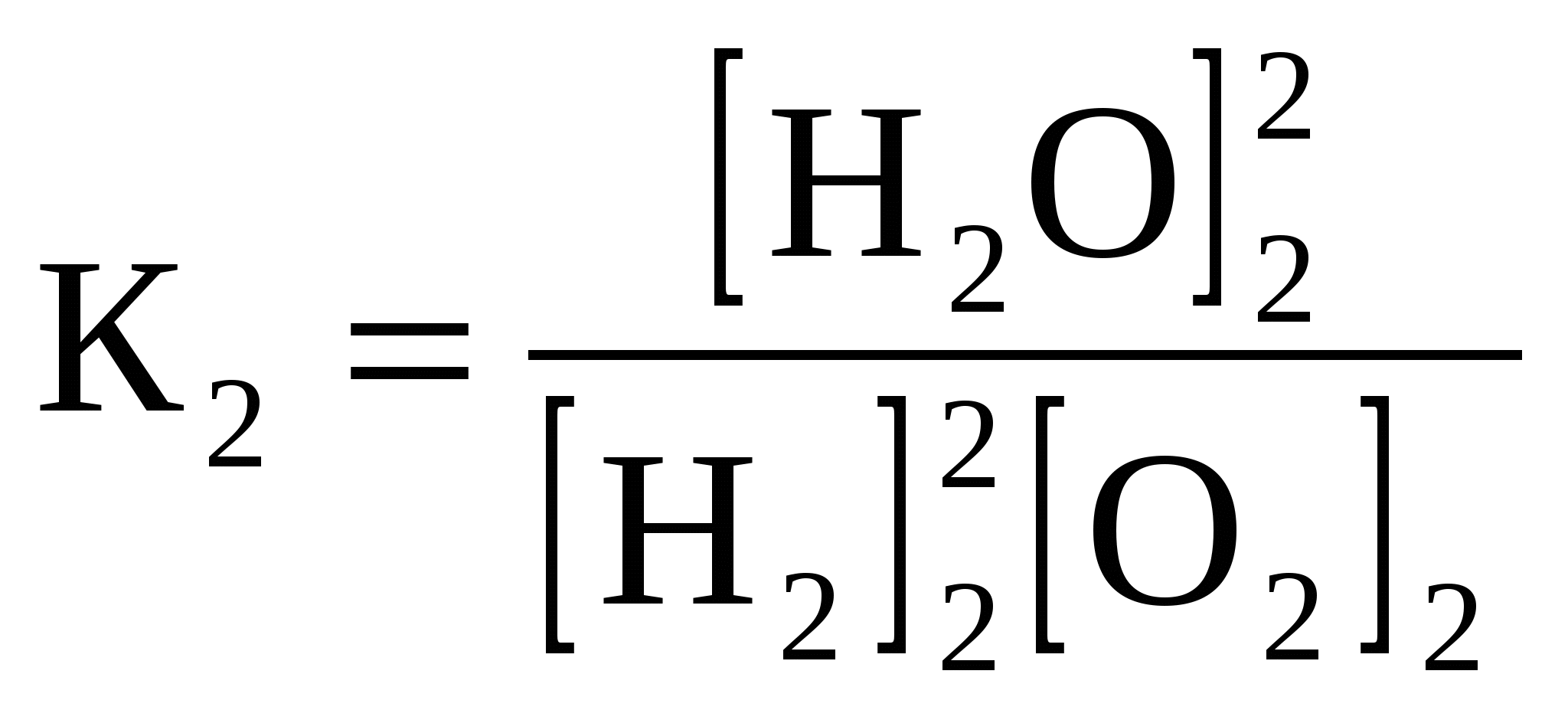 . .Спрашивается, как отличаются константы К1 и К2? Из принципа Ле-Шателье следует, что при повышении температуры равновесие смещается в сторону той реакции, которая ослабляет повышение температуры, а такой реакцией является процесс, идущий с поглощением тепла. Для данной системы это будет реакция диссоциации воды: 2Н2О = 2Н2 + О2 – Q. При повышении температуры равновесие смещается в сторону образования H2 и O2, т. е. с ростом температуры скорость взаимодействия кислорода и водорода замедляется, а скорость диссоциации воды возрастает, и это приводит к росту концентраций О2 и Н2 в равновесной газовой смеси. В реакции 2Н2 + О2 = 2Н2О + Q повышение температуры будет уменьшать константу равновесия, следовательно, [Н2О]1 [ Н2О]2, [H2]1 [H2]2, [O2]1 [O2]2. Отсюда вытекает общее правило: повышение температуры вызывает уменьшение константы равновесия реакции, идущей с выделением тепла (с уменьшением энтальпии), и увеличение константы равновесия реакции, сопровождающейся поглощением тепла (увеличением энтальпии). Направление смещения химического равновесия и изменение константы (увеличение или уменьшение её) определяется знаком теплового эффекта или знаком изменения энтальпии (см. таблицу 1.1). Таблица 1.1
Степень смещения равновесия определяется величиной теплового эффекта, или величиной изменения энтальпии. Чем больше эти величины, тем значительнее влияние температуры на константу равновесия. По степени изменения состояния равновесия при изменении температуры можно судить о тепловом эффекте реакции. Если известны две константы равновесия (К1 и К2) при двух температурах Т1 и Т2, то изменение энтальпии при протекании реакции вычисляют по следующей формуле: Данное уравнение широко используется в физико-химических расчетах для нахождения тепловых эффектов. Термохимические законы Закон Гесса Независимость теплоты химической реакции от пути процесса при р=const и Т=const была установлена в первой половине XIX века русским учёным Г.И. Гессом. Гесс сформулировал закон, который носит сейчас его имя: тепловой эффект химической реакции не зависит от пути ее протекания, а зависит лишь от природы и физического состояния исходных веществ и продуктов реакции. Этот закон справедлив для тех взаимодействий, которые протекают в изобарно-изотермических (или изохорно-изотермических) условиях при том, что единственным видом совершаемой работы является работа против сил внешнего давления. В термохимических уравнениях необходимо указывать агрегатные состояния веществ с помощью буквенных индексов, а тепловой эффект реакции (ΔН) записывать отдельно, через запятую. Например, термохимическое уравнение показывает, что данная химическая реакция сопровождается выделением 1531 кДж теплоты, при давлении 101 кПа, и относится к тому числу молей каждого из веществ, которое соответствует стехиометрическому коэффициенту в уравнении реакции. Важнейшей величиной в термохимии является стандартная теплота образования (стандартная энтальпия образования). Стандартной теплотой (энтальпией) образования сложного вещества называется тепловой эффект (изменение стандартной энтальпии) реакции образования одного моля этого вещества из простых веществ в стандартном состоянии. Стандартная энтальпия образования простых веществ в этом случае принята равной нулю. В термохимии используют уравнения, в которых тепловой эффект относят к одному молю образовавшегося вещества, применяя в случае необходимости дробные коэффициенты. Рассмотрим пример, поясняющий закон Гесса. Раствор сульфата натрия можно приготовить из растворов серной кислоты и гидроксида натрия двумя способами: 1. Смешать раствор, содержащий два моля NaOH, с раствором, содержащим один моль H2SO4.
Запишем термохимические уравнения этих реакций. Первый способ: 2NaOH(водн) + H2SO4(водн) = Na2SO4(водн) + 2H2O + 131,4 кДж. Второй способ: NaOH(водн.) + H2SO4(водн.) = NaHSO4(водн.) + 2H2O + 61,7 кДж, NaHSO4(водн.) + NaOH(водн.) = Na2SO4(водн.) + 2H2O + 69,7 кДж. Символ (водн.) означает, что вещество взято в виде водного раствора. Согласно закону Гесса, тепловой эффект в обоих случаях должен быть одним и тем же. Действительно, складывая тепловые эффекты, отвечающие двум стадиям второго способа, получаем тот же суммарный тепловой эффект, который наблюдается при первом способе проведения процесса: 61,7 + 69,7 = 131,4 кДж. Таким образом, подобно обычным уравнениям химических реакций, термохимические уравнения можно складывать. В основе большинства термохимических расчетов лежит следствие из закона Гесса: тепловой эффект химической реакции равен сумме теплот (энтальпий) образования продуктов реакции за вычетом суммы теплот (энтальпий) образования исходных веществ с учетом коэффициентов, стоящих перед веществами в термохимическом уравнении реакции:
Величины стандартных энтальпий образования веществ приведены в справочной таблице приложения. Уравнение (1.11) позволяет определять как тепловой эффект реакции по известным величинам стандартных энтальпий образования веществ, участвующих в реакции, так и одну из энтальпий образования, если известны тепловой эффект реакции и все остальные энтальпии образования. Пример 2. Рассчитать стандартный тепловой эффект реакции ½Na2O(к) + ½Н2O(ж) = NaOH(к) по известным величинам стандартных энтальпий образования веществ (см. таблицу приложения). Записать термохимическое уравнение реакции. Решение. На основании следствия из закона Гесса можно записать: ∆H0298 = ∆H0298 обр.(NaOH) – [½∆H0298 обр.(Na2O) + ½∆H0298 обр.(H2O)]. Подставив в это выражение значения стандартных энтальпий образования веществ с учётом их агрегатных состояний, получим для NaOH ∆H0298 = -426,60 + 215,30 + 142,92 = -68,38 кДж/моль. Термохимическое уравнение реакции следует записать так: ½Na2O(к) + ½Н2O(ж) = NaOH(к), ∆H0298 = –68,38 кДж/моль или так: ½Na2O(к) + ½Н2O(ж) = NaOH(к) + 68,38 кДж/моль. Пример 3. Стандартный тепловой эффект реакции 2А + В = 2С равен 150 кДж/моль. Рассчитать стандартную теплоту (энтальпию) образования вещества А, если ∆H0298 обр.(В) = –45,0 кДж/моль и ∆H0298 обр.(С) = –60 кДж/моль. Решение. На основании следствия из закона Гесса для рассматриваемой реакции имеем: ∆H0298 = 2∆H0298 обр C – ( 2∆H0298 обр. A + ∆H0298 обр. B). Подставив в это выражение приведенные в условии задачи значения ∆H, определим величину ∆H0298 обр. (A): ∆H0298 обр. A = ½ (-150-120+45) = - 112,5 кДж/моль. Пример 4. При восстановлении 12,7 г оксида меди (II) углем (с образованием СО) поглощается 8,24 кДж. Определить ∆H0298 обр CuO. Решение. CuO + C → Cu + CO. Согласно следствию из закона Гесса имеем: ∆H0298 = (∆H0298 обр Cu + ∆H0298 обр.CO) – ∆H0298 обр. СuO, откуда ∆H0298 обр CuO = - ∆H0298 + ∆H0298 обр Cu + ∆H0298 обр СО. Произведем пересчет теплового эффекта восстановления 1 моль оксида меди: при сгорании 12,7 г СuO поглощается 8,24 кДж; при сгорании 79,5 г СuO поглотится х кДж. Решая эту пропорцию, получим х = 51, 58 кДж. (Молярная масса оксида меди (II) М = 79,5 г/моль). Произведем подстановку полученного значения в выражение для нахождения ∆H0298 обр CuO: ∆H0298 обр CuO = -51,58 – 110,5 = -162,1 кДж. Пример 5. Вычислить тепловой эффект реакции сгорания метана СН4, зная теплоты образования метана (74,9 кДж/моль) и продуктов его сгорания – диоксида углерода (393,5 кДж/моль) и воды (285,8 кДж/моль). Решение. Для вычисления запишем реакцию горения метана сначала непосредственно, а затем разбив на стадии. Соответствующие термохимические уравнения будут иметь вид: СН4 + 2О2 = СО2 + 2Н2О + х кДж; СН4 = С (графит) + 2Н2 – 74,9 кДж; С (графит) + О2 = СО2 + 393,5 кДж; 2Н2 + О2 = 2Н2О +2∙285,8 кДж. Складывая последние три термохимические уравнения, отвечающие проведению реакции по стадиям, получим суммарное уравнение горения метана: CН4 + 2О2 = СО2 + 2Н2О + (- 74,9 + 393,5 + 571,6) кДж. Согласно закону Гесса, - 74,9 + 393,5 + 571,6 = х, откуда теплота сгорания метана х = 890,2 кДж. Закон Кирхгофа В термодинамических таблицах содержатся стандартные энтальпии (изобарные тепловые эффекты, изобарные теплоты) образования химических соединений из простых веществ при 25С. При температурах, отличных от 25С, тепловые эффекты в общем случае будут иными. Причем для различных реакций влияние температуры на тепловой эффект неодинаково. Только в одном случае, когда суммы теплоёмкостей исходных веществ и продуктов реакции равны, температура не влияет на тепловой эффект реакции. Чем сильнее отличаются теплоёмкости исходных веществ от теплоёмкостей продуктов, тем сильнее сказывается влияние температуры на тепловой эффект реакции. Зависимость теплот химических реакций от температуры была изучена Кирхгофом. Эта зависимость выражается уравнением
где ∆С – разность сумм теплоемкостей продуктов реакции и исходных веществ, взятых с учетом стехиометрических коэффициентов. Так как чаще всего процессы протекают при постоянном давлении, то обычно применяют уравнение (1.12), в котором Qp = ∆H и ∆С = ∆Сp. В этом случае интегрирование уравнения (1.12) дает известное уравнение Кирхгофа
где ∆H0298 – стандартный тепловой эффект реакции при Т=298 К; ∆H0Т – стандартный тепловой эффект реакции при температуре Т; ΔСр – разность мольных изобарных теплоёмкостей всех продуктов реакции и мольных изобарных теплоёмкостей всех исходных веществ. Закон Кирхгофа можно сформулировать так: изменение энтальпии в реакции при температуре Т2 равно изменению ее при температуре Т1 плюс разность мольных теплоемкостей продуктов реакции и исходных веществ, умноженная на изменение температуры. Расчеты по уравнению Кирхгофа показывают, что в том интервале температур, который может иметь практическое значение, изменение величины теплового эффекта реакции невелико. Так, например, тепловой эффект реакции Cu(к) + ½О2(г) = СuO(к), протекающей при р = 101 кПа, меняется с температурой следующим образом: Т1=298 К; ∆H0298 = - 156,9 кДж/моль; Т2=500 К; ∆H0298 = - 155,5 кДж/моль; Т3=1000 К; ∆H0298 = - 149,5 кДж/моль. Тепловой эффект процесса ½N2 + ½O2 = NO(г) при повышении температуры от 298 до 4000 К изменяется на 2,0 кДж/моль. Еще меньше влияние давления на тепловой эффект реакции. Так, для реакции синтеза аммиака из азота и водорода (все реагенты - газы) различие между величинами ∆HТ при р=101 кПа и р=50 МПа не превышает 5%. Поэтому при выполнении термохимических расчетов, допуская обычно незначительную ошибку, можно пользоваться стандартными значениями теплот образования даже тогда, когда условия протекания процесса отличаются от стандартных. Закон Лавуазье-Ломоносова-Лапласа Тепловой эффект образования сложного вещества равен по величине и противоположен по знаку тепловому эффекту процесса разложения этого вещества. Например: Н2 + ½О2 = Н2О(г) + 241,83 кДж/моль; Н2О (газ) = Н2 + ½О2 – 241,83 кДж/моль. Знак изменения энтальпии или внутренней энергии в тех же самых процессах противоположен, и если провести термодинамическую запись рассмотренных выше уравнений, то она будет выглядеть так: Н2 + ½О2 = Н2О(г) (ΔНо = -241, 83 кДж/моль); Н2О(г) = Н2 + ½О2 (ΔНо = +241, 83 кДж/моль). Тепловые эффекты фазовых превращений Фазовые превращения часто сопутствуют химическим реакциям. Однако тепловые эффекты таких превращений, как правило, меньше тепловых эффектов химических реакций. Ниже приведены примеры термохимических уравнений некоторых фазовых превращений: H2O(ж) H2O(ж) H2O(к) J2(к) Тепловой эффект реакции зависит от агрегатных состояний и модификаций исходных веществ и продуктов реакции. И если, например, взаимодействие йода с водородом, которое протекает по уравнению ½J2 + ½Н2 = HJ, может сопровождаться или поглощением теплоты ∆H0298 = +25,94 кДж/моль, или ее выделением ∆H0298 = -5,18 кДж/моль, то это значит, что в первой реакции участвует кристаллический йод, а во второй – газообразный: ½J2(к) + ½Н2(г) = HJ(г), ∆H0298 = +25,94 кДж/моль; ½J2(г) + ½Н2(г) = HJ(г), ∆H0298 = -5,18 кДж/моль. Направленность химических процессов Химические процессы могут протекать самопроизвольно (без затрат энергии извне) и несамопроизвольно (требуют для своего осуществления затрат энергии). Направление, в котором самопроизвольно протекает химическая реакция, определяется совместным действием двух факторов: 1) стремлением системы к минимуму энергии (при Р = const - к минимуму энтальпии); 2) стремлением системы к достижению наиболее вероятного состояния, т.е. состояния, которое может быть реализовано наибольшим числом равновероятных способов (микросостояний, характеризующихся определенным состоянием каждой частицы, входящей в состав системы). Функцией состояния, одновременно отражающей влияние обеих упомянутых выше тенденций на направление протекания химических процессов, служит энергия Гиббса, связанная с энтальпией и энтропией соотношением
где Т - абсолютная температура (К). Энергия Гиббса имеет ту же размерность, что и энтальпия, и выражается, в джоулях (Дж) и килоджоулях (кДж). Уравнение, отражающее связь возможности протекания химической реакции в системе с происходящими при этом изменениями Н и S, имеет вид:
где ΔG°х.р. — изменение стандартной энергии Гиббса химической реакции или просто стандартная энергия Гиббса химической реакции. Как и в случае с ΔН, изменение энтропии ΔS0х.р. и изменение энергии Гиббса ΔG0х. р. рассчитываются с использованием следствия закона Гесса (суммирование производят с учетом числа молей участвующих в реакции веществ):
При постоянстве температуры и давления химические реакции могут протекать самопроизвольно только в таком направлении, при котором энергия Гиббса системы уменьшается (ΔG0х.р. < 0). Чем меньше ΔG0х.р., тем больше вероятность протекания данного процесса. При ΔG0 х.р. > 0 реакция самопроизвольно не идет в прямом направлении, но возможно самопроизвольное протекание в обратном направлении. Таким образом, ΔG0 х.р., является критерием направленности химических процессов. Если для какой-то реакции ΔН < 0 (экзотермическая реакция), а ΔS > 0, то в соответствии с уравнением следует, что реакция может самопроизвольно протекать при любых температурах. Если ΔН < 0 и ΔS < 0, то реакция возможна при условии, что член ΔН в уравнении для энергии Гиббса больше по абсолютному значению, чем член ТΔS; поскольку абсолютное значение члена ТΔS с ростом множителя Т увеличивается, то указанное условие будет действовать при достаточно низких температурах. Иначе говоря, при низких температурах наиболее вероятно самопроизвольное протекание экзотермических реакций, даже если при этом энтропия системы уменьшается. При высоких температурах наиболее вероятно протекание реакций, сопровождающихся возрастанием энтропии, в том числе и эндотермических. Если ΔG0 х.р. = 0, то это соответствует термодинамическому условию равновесия в системе, откуда можно найти температуру, при которой наступит равновесие в системе:
Для определения возможности протекания процесса при данных условиях надо определить знак ΔG0х.р..С этой целью в справочных таблицах термодинамических величин находятся стандартные значения ΔH0обр и ΔS0обр веществ, участвующих в реакции, по которым вычисляют ΔG0х.р. в соответствии с приведенной выше формулой. Для расчета можно также использовать табличные значения ΔG0обр образования химических соединений, которые соответствуют изменению энергии Гиббса реакции образования 1 моль данного вещества в стандартном состоянии из простых веществ, также взятых в стандартных состояниях. Величины ΔG0обр образования простых веществ приняты равными нулю. Табличные значения стандартных величин ΔG0обр образования простых веществ приводятся для 25°С (298 К) и обозначаются ΔG0обр, с указанием соединения, к которому они относятся. Например: ΔG0обр Fe2O3(к) = -740,8 кДж/моль. Пример 6. Можно ли получить металлический кадмий из сульфида кадмия (П) восстановлением оксида углерода (II) по реакции: 2CdS(к) + 2СО(г) = СО2(г) + CS2(г) + 2Cd(к). Решение. Ответ на вопрос задачи дает вычисление энергии Гиббса, рассматриваемой реакции. Проще всего воспользоваться табличными значениями энергии Гиббса образования соответствующих веществ: ΔG0обр CdS = -153,16 кДж/моль; ΔG0обр CO = -137,15 кДж/моль; ΔG0обр CO2 = -394,37 кДж/моль; ΔG0обр CS2 = 66,65 кДж/моль. Вычисляем ΔG0 х.р. (химической реакции) используя уравнение (1.17): ΔG0 х.р = ΔG0обр CO2 + ΔG0обр CS2 – 2 ΔG0обр CdS - 2 ΔG0обр CO ΔG0 х.р = -394,37 + 66,65 -- 2(-153,16) - 2(-137,15) = 252,88 кДж. ΔG0х.р. > 0, следовательно, данная реакция в стандартных условиях протекать не может, и металлический кадмий таким способом получить нельзя. Пример 7.Прямая или обратная реакция будут протекать при стандартных условиях в системе: 2NO2(г) = 2NO(г) + О2(г), ΔН0х.р. = 113,2 кДж. Решение. Для ответа на этот вопрос следует вычислить ΔG0х.р. прямой реакции: ΔG0х.р. = ΔН0х.р. - TΔS0 х.р., ΔН0х.р. по условию задачи известно, Т = 298К, так как условия стандартные. Следовательно, необходимо вычислить ΔS0х.р, используя табличные значения энтропии соответствующих веществ: S0обр NO2 = 240,5 Дж/(моль·К); S0обр O2 = 205,0 Дж/(моль·К); S0обр NO = 210,6 Дж/(моль·К ). Используя уравнение (1.16) находим ΔS0х.р.: ΔS0х.р. = 2S0обр NO + S0обр O2 - 2S0обр NO2 ΔS0х.р. = 2·210,6 + 205,0 - 2·240,5 = 145,2 Дж/К. На основании уравнения (1.15) вычисляем ΔG0х.р., подставляя ΔН0х.р и ΔS0х.р., переводя при этом Дж в кДж: ΔG0х.р. = 113,2 - 298 (145,2/1000) = 70,0 кДж. ΔG0х.р. > 0, следовательно, самопроизвольно в стандартных условиях может протекать только обратная реакция. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
