ЛАБОРАТОРНЫЙ ПРАКТИКУМ ПО ХИМ ТЕРМОДИНамиКЕ. Практикум по химической термодинамике учебное пособие для студентов всех специальностей

• Название: Практикум по химической термодинамике учебное пособие для студентов всех специальностей
• Анкор: ЛАБОРАТОРНЫЙ ПРАКТИКУМ ПО ХИМ ТЕРМОДИНамиКЕ.doc
• Дата: 19.05.2017
• Размер: 2.28 Mb.
• Имя файла: ЛАБОРАТОРНЫЙ ПРАКТИКУМ ПО ХИМ ТЕРМОДИНамиКЕ.doc
• Тип: Практикум; #7896
• страница: 9 из 15

Двухкомпонентные системы
Состав двойных систем можно изобразить в виде отрезка прямой, длина которого принимается за единицу при выражении состава в атомных, мольных, массовых долях или за 100 – при выражении состава атомных, мольных или массовых процентах.


Рис. 3.3. Ось состава двойной системы
На рис. 3.3 изображена ось состава в виде отрезка прямой АВ, на котором точке А соответствует чистый компонент А (одна доля или 100 %), а точке В – чистый компонент В. По мере удаления от точки А вправо в смеси уменьшается содержание компонента А и увеличивается содержание компонента В. Например, состав смеси, изображенный фигуративной точкой Q, отвечает AQ процентам (долям) компонента В и QВ –процентам(долям)компонента А.Для оси состава двойнойсистемы при выражении этого состава в процентах (долях) можно применять правило рычага, устанавливающее зависимость между соотношением масс смесей различного состава и отношением отрезков на оси состава. Допустим, что взято q₁ массовых единиц смеси состава, изображенного фигуративной точкой Q₁, и q₂ массовых единиц смеси Q₂. При смешении их получим новую смесь Q, масса которой равна q = q₁ + q₂.В соответствии с правилом рычага q₁/ q₂ = Q Q₂/ Q₁ Q.

При помощи правила рычага возможно решение ряда задач, связанных с расчетом составов смесей веществ.
Пример 1. Cмешано3г смеси,содержащей0,8мас.долей компонентаА и5г смеси,содержащей0,2мас.доли компонента А.Каков составполученной смеси?

Решение. По правилу рычага 5/3 = Q₁ Q / Q Q₂ = (0,8 – х) / (х – 0,2). Отсюда х = 0,425. Таким образом, полученная смесь содержит 0,425 мас. долей компонента А.
Пример 2.Предположим,что необходимо получить9г смеси,содержащей 0,5 мас. доли А, из смеси, содержащей 0,7 мас. доли А и 0,4 мас. доли А. Сколько по массе нужно взять этих смесей?

Решение. По правилу рычага

q₁/ q₂ = Q Q₂/ Q ₁Q = (x₂– x) / (x – x₁);

q₁/ (9 – q₁) = (0,7 – 0,5) / (0,5 – 0,4) = 0,2 / 0,1.

Отсюда q₁ = 6 г, q₂ = 3 г.
Для двухкомпонентной системы, на которую из внешних условий оказывают влияние давление и температура, правило Гиббса выражается уравнением

С= 4 – Ф.

(3.14)

Следовательно, в двухкомпонентных системах число фаз, находящихся в равновесии, не может быть больше четырех (С = 0, если Ф = 4), а максимальное число независимых параметров состояния системы, то есть термодинамических степеней свободы, равно трем: давление, температура и концентрация одного из компонентов, выраженная в массовых или молярных долях или процентах (С = 3, если Ф = 1).

Для выяснения характера взаимодействия между компонентами и выявления областей существования и состава равновесных фаз требуется построение трехмерной диаграммы, поскольку состояние двухкомпонентной системы определяется тремя параметрами (температура, давление, концентрация одного из компонентов). Однако чаще используют плоские диаграммы, получаемые при постоянстве одного из трех параметров. Рассмотрим несколько диаграмм состав – свойство для двухкомпонентных систем.
Равновесие пар – жидкий раствор
Рассмотрим диаграммы кипения для некоторых реальных систем при Р = const (рис. 3.4, 3.5).На этих диаграммах фигуративные точки а и b соответствуют температурам кипения чистых компонентов А и В при данном внешнем давлении Р. При температуре кипения чистого компонента система условно инварианта (С_усл = 1 – 2 + 1 = 0). Та из двух жидкостей, которая обладает более низкой температурой кипения при заданном внешнем давлении, будет более летучей при данной температуре, т.е. чем ниже температура кипения жидкости, тем выше давление пара над ней. Каждая из диаграмм кипения имеет две кривые, разделяющие диаграмму на три области:

I – область пара (С_усл = 2 – 1 + 1 = 2),

II – область жидкости (С_усл = 2 – 1 + 1 = 2),

III – область равновесия пара и жидкости (С_усл = 2 – 2 + 1 = 1).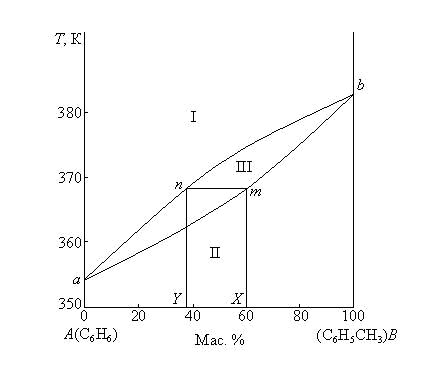


Рис. 3.4. Диаграмма кипения системы бензол – толуол

при P = 1,0133·10⁵Па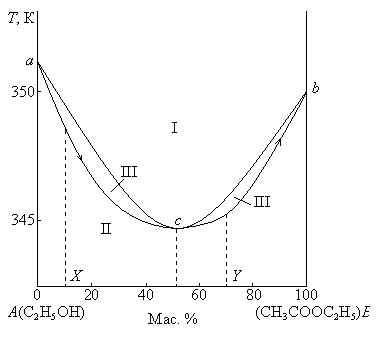



Рис. 3.5. Диаграмма кипения системы этиловый спирт – этилацетат

при P = 1,0133·10⁵Па
Фигуративные точки, лежащие на кривой жидкости (нижняя кривая), характеризуют составы кипящих жидкостей и температуры, при которых начинают кипеть жидкости заданного состава. Например, фигуративная точка m (рис. 3.4) показывает, что раствор состава X начинает кипеть при 368 К. Фигуративные точки, лежащие на кривой пара (верхняя кривая), характеризуют составы пара и температуры, при которых исчезают последние капли жидкости при кипении исходных смесей. Например, фигуративная точка n (рис.3.4) отвечает составу (Y) первого пузырька пара, полученного при кипении раствора т состава X. С другой стороны, точка п показывает температуру 368 К, при которой исчезает последняя капля жидкости при кипении раствора состава Y. Количества равновесных фаз для исходных смесей, находящихся между линиями пара и жидкости, определяются по правилу рычага как обычно в двухкомпонентных системах.

Реальные растворы со значительным положительным или отрицательным отклонением от идеального способны образовывать азеотропные смеси (азеотропы). Так на рис. 3.5 азеотропная смесь изображена точкой с. Азеотропные смеси – это растворы, при испарении которых получается пар того же состава, что и исходная жидкая смесь (X_(п) = X_(ж)). Азеотропные смеси – условно инвариантные системы (С_усл = 2 – 2 = 0). В реальных растворах азеотропная смесь имеет самую низкую или самую высокую температуру кипения (рис. 3.5). При изменении внешнего давления изменяется не только температура кипения, но и состав азеотропного раствора. Это указывает на то, что азеотропная смесь не является химическим соединением.

Как для идеальных, так и для реальных растворов справедлив первый закон Гиббса – Коновалова:пар по сравнению с жидким раствором,изкоторого он получен, при равновесии богаче тем компонентом, прибавление которого к раствору приводит к понижению температуры кипения раствора при заданном внешнем давлении или к повышению давления пара над раствором. Следует отметить, что в системах с азеотропными смесями добавление к раствору более летучего компонента не всегда приводит к повышению давления пара над раствором, т.е. к понижению температуры кипения раствора. Так, при добавлении к растворам, находящимся левее точки с (рис.3.4), более летучего компонента В температура кипения раствора понижается, а следовательно, повышается давление пара над раствором. При добавлении компонента В к растворам, находящимся правее точки с, температура кипения раствора повышается, а давление пара над раствором понижается, при этом пар богаче компонентом А.

Для реальных растворов с азеотропными смесями справедлив также второй закон Гиббса – Коновалова:в азеотропных смесях,изображенныхна диаграммах состояния экстремальными точками (максимум или минимум), составы жидкости и пара совпадают.

Законы Гиббса – Коновалова были выведены теоретически Дж. Гиббсом и независимо открыты экспериментальным путем Д.П. Коноваловым (1881).

Азеотропные смеси образуются не только в системах со значительными отклонениями от закона Рауля, но и в системах с незначительными отклонениями, когда компоненты раствора имеют близкие температуры кипения, т.е. почти одинаковые давления пара над чистыми компонентами (). В этом случае на диаграмме состояния появляется экстремум, лежащий в средней части диаграммы. Чем больше различие между и , тем больше положение экстремума сдвинуто в сторону одного из компонентов системы: при максимуме на кривой давления пара в сторону более летучего компонента, при минимуме – в сторону менее летучего компонента.
Двухкомпонентные конденсированных системы
К основным типам диаграмм состояния двухкомпонентных конденсированных систем относятся:

• 
  диаграмма с простой эвтектикой;
  
• 
  диаграмма с образованием устойчивого химического соединения (конгруэнтно плавящегося);
  
• 
  диаграмма с образованием неустойчивого химического соединения (инконгруэнтно плавящегося);
  
• 
  диаграмма с неограниченной взаимной растворимостью компонентов в твердом состоянии;
  
• 
  диаграмма с ограниченной растворимостью компонентов в твердом состоянии (I и II вида);
  
• 
  диаграмма с ограниченной взаимной растворимостью компонентов в жидком состоянии.
  

Для изучения равновесия кристаллы – жидкий раствор широко применяются диаграммы плавкости, выражающие зависимость температур плавления смесей от их состава. Частным случаем диаграмм плавкости являются диаграммы растворимости, характеризующие зависимость растворимости твердых веществ в жидкостях от температуры.

Вид диаграмм плавкости определяется взаимной растворимостью компонентов в жидком и твердом состояниях.
Диаграмма состояния системы с эвтектикой
Наиболее проста диаграмма состояния системы, в которой компоненты неограниченного смешиваются в жидком состоянии, совершенно не смешиваются в твердом, химически не взаимодействуют друг с другом и не образуют твердых растворов.

Образование таких диаграмм наблюдается, как правило, в том случае, когда компоненты А и В имеют разные типы кристаллических решеток и различные размеры радиусов частиц решетки, или при наличии одинакового типа решетки резко различные радиусы частиц.

В системах, не образующих химических соединений, при охлаждении расплава любого состава всегда кристаллизуются чистые компоненты. Диаграмма плавкости для одной из таких систем приведена на рис. 3.6.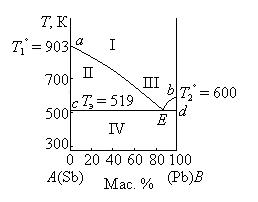



Рис. 3.6. Диаграмма плавкости системы Sb – Pb при Р = const
На данной диаграмме фигуративные точки а и b изображают температуры плавления (кристаллизации) чистых компонентов А и В (T₁^o и T₂^o).При этих температурах системы условно инварианты(С_усл= 1 – 2 + 1= 0). При температурах выше T₁^o или T₂^o соответствующие чистые компоненты находятся в расплаве (С_усл = 1 – 1 + 1 = 1), при температурах ниже T₁^o или T₂^o – в твердом состоянии (С_усл =1 – 1 + 1 = 1). Фигуративные точки, лежащие на кривых аЕ и bЕ, характеризуют температуры, при которых из жидких расплавов начинается кристаллизация компонента А или В. Эти температуры ниже соответственно T₁^o или T₂^o. Одновременно фигуративные точки, лежащие на кривых аЕ и bЕ, изображают составы жидких расплавов, при охлаждении которых начинается кристаллизация из расплава чистого компонента А или В. Линии аЕ и bЕ называются линиями ликвидуса (от латинского словаliguor –жидкость).

В отличие от чистых компонентов кристаллизация (плавление) большинства двухкомпонентных систем происходит не при постоянной температуре, а в температурном интервале, который определяется составом системы. Минимальная температура, при которой заканчивается кристаллизация расплава любого состава (или начинается плавление твердой двухкомпонентной системы), называется эвтектической температурой (T_э). Линия cd, отвечающая эвтектической температуре (ниже которой не может существовать жидкая фаза), называется линией солидуса (от латинского словаsolid –твердый).Фигуративная точка Е –точка пересечения линий ликвидуса с линией солидуса – характеризует состав расплава, который находится в равновесии одновременно с кристаллами компонентов А и В. Точка Е называется эвтектической точкой, а соответствующий расплав – эвтектическим расплавом. Смесь кристаллов компонентов А и В, выпадающая из этого расплава при температуре T_э, называется эвтектической смесью или просто эвтектикой (от греческого слова eutektik – хорошо плавящийся). Эвтектика кристаллизуется при постоянной температуре, система условно инвариантна (С_усл = 2 – 3 + 1 = 0). В этом состоит сходство эвтектики с чистыми компонентами. Однако между эвтектикой и чистыми компонентами есть и различия. Главное различие состоит в том, что при изменении давления, как следует из правила фаз, меняется и температура плавления, и состав эвтектики, тогда как у чистых компонентов изменяется только температура плавления. Кроме того, при кристаллизации чистого компонента из его расплава состав твердой фазы одинаков с составом жидкого расплава. При кристаллизации эвтектики состав жидкого расплава отличается от состава каждой из равновесных с ним твердых фаз.

Линии ликвидуса и солидуса делят диаграмму плавкости на ряд областей:

I – жидкий расплав (С_усл = 2 – 1 + 1 = 2),

II – жидкий расплав и кристаллы компонента А (С_усл = 2 – 2 + 1 = 1),

III – жидкий расплав и кристаллы компонента В (С_усл = 2 – 2 + 1 = 1),

IV – кристаллы компонентов А и В (С_усл = 2 – 2 + 1 = 1).

При температурах ниже эвтектической система условно моновариантна. При сохранении постоянства состава равновесных твердых фаз произвольно можно изменять только температуру.

Диаграммы плавкости с простой эвтектикой, состоящей из чистых компонентов, встречаются довольно часто среди металлических, солевых, органических систем, например, системы Ag – Pb, Zn – Sn, Bi – Cd, KCl – LiCl, AgBr – KBr, хлорид бензоила – дифенил. Диаграммы состояния аналогичного вида характерны и для многих водных солевых систем (диаграммы растворимости), при охлаждении которых кристаллизуются эвтектические смеси, состоящие из воды и солей, называемые криогидратами. Например, системы NH₄C1 – H₂O, NaNO₃ – Н₂О. Явления, связанные с образованием и свойствами эвтектик, известны очень давно. Эвтектики широко применяются для практических целей. Так, для пайки свинцовых водопроводных труб издавна используется легкоплавкий припой – третник, состоящий из двух частей олова и одной части свинца, очень близкий по составу к эвтектическому сплаву этих металлов. Эвтектические смеси, действие которых основано на поглощении теплоты при образовании жидких эвтектик из некоторых солей и снега, применяются и для получения искусственного холода. Например, смесь шестиводного хлорида кальция со снегом дает понижение температуры до – 50°С.
Системы с образованием химических соединений,

плавящихся конгруэнтно
Плавление называется конгруэнтным (от латинского слова congruentis – совпадающий), если состав жидкости совпадает с составом твердого химического соединения, из которого жидкость образовалась. Такие химические соединения являются устойчивыми и плавятся без разложения. Диаграмма плавкости двухкомпонентной системы с образованием одного химического соединения, плавящегося конгруэнтно, на которой указаны области существования и равновесные фазы, приведена на рис. 3.7.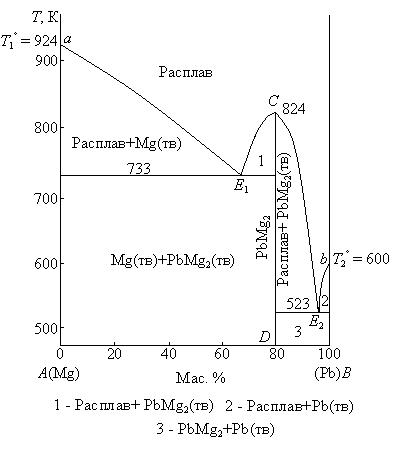


Рис. 3.7. Диаграмма плавкости системы Mg – Pb при Р = const:

1 – расплав + PbMg_2(тв); 2 – расплав + Pb_(тв); 3 – PbMg_2(тв) + Pb_(тв)
Эта диаграмма по сути является сочетанием двух диаграмм плавкости, каждая из которых имеет одну эвтектику. Так как в рассматриваемой системе Mg – Pb образуется одно химическое соединение, то из расплава могут кристаллизоваться три твердые фазы: компонент A (Mg), компонент В (Рb)и химическое соединениеPbMg₂.Прибавление магния или свинцак химическому соединению приводит к понижению температуры начала кристаллизации из расплава химического соединения. В связи с этим линия ликвидуса Е₁СЕ₂ конгруэнтно плавящегося химического соединения имеет максимум (фигуративная точка С), отвечающий температуре плавления (кристаллизации) химического соединения. Положение этого максимума строго соответствует составу образующегося химического соединения. Система, изображенная диаграмме фигуративной точкой С, условно инвариантна (С_усл = 1 – 2 + 1 = 0). Фигуративные точки, лежащие на линии CD, соответствуют твердому химическому соединению при разных температурах (С_усл = 1 – 1 + 1 = 1). В различных системах вид максимума кривой плавкости химического соединения разный и зависит от степени диссоциации соединения при температуре плавления, протекающей по схеме

.

(3.15)

Чем больше степень диссоциации химического соединения, тем более пологим будет этот максимум. Чем меньше степень диссоциации химического соединения, тем острее максимум на кривой плавления. В пределе, когда степень диссоциации равна нулю, радиус кривизны линий ликвидуса Е₁С и Е₂С превращается в нуль, что отвечает острому максимуму. Фигуративная точка С, отвечающая недиссоциированному химическому соединению, называется сингулярной, или дальтоновской точкой. Характерной особенностью сингулярных точек является то, что при изменении условий равновесия (в частности, температуры или давления) отвечающий им состав не изменяется. Примерами систем с одним конгруэнтно плавящимся соединением являются системы Sn – Mg, Mg – Si, CaCl₂ – KCl.

Если компоненты А и В образуют несколько химических соединений, плавящихся конгруэнтно, на диаграмме плавкости каждому химическому соединению отвечает свой максимум. Примерами систем с образованием нескольких химических соединений, плавящихся конгруэнтно, являются системы Ag – Ca, Ce – Sn, Cu – Mg, Al₂O₃ – СаО, РbО – PbCrO₄, Ag₂S – Sb₂S₃, Na₂O – SiO₂.
Системы с образованием химических соединений,

плавящихся инкогруэнтно
Плавление называется инконгруэнтным (от латинского слова incongruentis – несовпадающий), если состав жидкости не совпадает с составом твердого химического соединения, из которого жидкость образовалась. Такие химические соединения являются неустойчивыми и разлагаются при более низких температурах, чем их температура плавления. Диаграмма плавкости двухкомпонентной системы с образованием одного химического соединения, плавящегося инконгруэнтно, на которой указаны области существования и равновесные фазы в системе, приведена на рис. 3.8.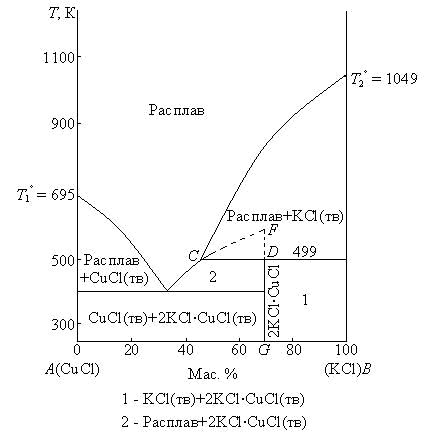


Рис. 3.8. Диаграмма плавкости системы CuCl – KCl при Р = const:

1 – KCl_(тв) + 2KCl·CuCl_(тв); 2 – расплав + 2KCl·CuCl_(тв).
При образовании химического соединения, плавящегося инконгруэнтно, максимум, отвечающий температуре плавления этого соединения (фигуративная точка F), не реализуется и попадает в область, находящуюся под линией ликвидуса одного из компонентов (в системе CuCl – КСl компонента В). Такой максимум называется скрытым. Это связано с тем, что химическое соединение устойчиво только до температуры, отвечающей фигуративной точке D. При этой температуре химическое соединение распадается на жидкий расплав (фигуративная точка С) и кристаллы компонента В. Точка С называется переходной, или перитектической точкой.В процессе распада химического соединениярасплав находится в равновесии с двумя твердыми фазами (химическое соединение и компонент В), поэтому система условно инвариантна (С_усл = 2 – 3 + 1 = 0). При исчезновении кристаллов химического соединения система становится условно моновариантной (C_усл =2 – 2 + 1 = 1). Линия DG –линия твердого химического соединения(С_усл= 1 – 1 + 1 = 1).Примерами систем с одним инконгруэнтно плавящимся соединением являются системы К – Na, Au – Sb, C₆H₅I – SbCl₃.

Если компоненты А и В образуют несколько химических соединений, плавящихся инконгруэнтно, на диаграмме плавкости каждому химическому соединению отвечает свой скрытый максимум. Примерами систем с образованием нескольких химических соединений, плавящихся инконгруэнтно, являются системы ZnCl₂ – H₂O, MgSO₄ – H₂O, MgCl₂ – H₂O.
Системы с неограниченной растворимостью компонентов в жидком и ограниченной взаимной растворимостью в твердом состояниях
В системах, в которых оба компонента неограниченно растворимы в жидком состоянии, ограниченно растворимы в твердом состоянии и не образуют химических соединений, из расплавов кристаллизуются не чистые компоненты, а твердые растворы. Таким образом, в системах такого рода возможно существование трех фаз:

• 
  расплава;
  
• 
  твердого раствора α– внедрение компонента Вв кристаллическую решетку компонента А;
  
• 
  твердого раствора β – внедрение компонента А в кристаллическую решетку компонента В.
  

Диаграммы состояния таких систем могут быть двух типов:

1. Диаграмма с эвтектикой (I типа) – твердые растворы образуют эвтектическую смесь (рис. 3.8).

2. Диаграмма с перитектикой (II типа) – твердые растворы образуют перитектическую смесь (один из твердых растворов устойчив только до определенной температуры) (рис. 3.9).
Диаграммы состояния с ограниченной растворимостью компонентов в твердом состоянии с эвтектикой (I типа).

Рассмотрим фазовую диаграмму образования твердых растворов с ограниченной растворимостью компонентов и с образованием эвтектической смеси (рис. 3.9).

В такой системе не образуются фазы, представляющие собой чистые компоненты. Из расплава могут кристаллизоваться только твердые растворы α или β.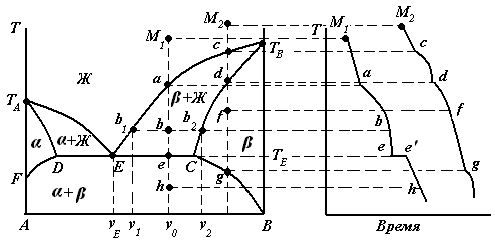



Рис. 3.9. Диаграмма состояния системы с ограниченной растворимостью компонентов в твердом состоянии с эвтектикой

Значение полей
Ж	расплав
α	кристаллы твердого раствора α
β	кристаллы твердого раствора β
α + Ж	расплав + кристаллы твердого раствора α
β + Ж	расплав + кристаллы твердого раствора β
α + β	механическая смесь кристаллов твердых растворов α и β
Значение линий
ТАЕ и ЕТВ	линии ликвидуса, каждая точка линий показывает состав расплава, равновесного с твердыми растворами α и β соответственно
ТАD и ТВС	линии солидуса, каждая точка линий показывает составы твердых растворов α и β, равновесных с расплавом
DF	состав равновесного твердого раствора α, определяющий предельную растворимость В в А
CB	состав равновесного твердого раствора β, определяющий предельную растворимость А в В
DЕC	линия эвтектики (ниже этой линии жидкой фазы нет)
Значение точек
ТА		температура плавления компонента А
ТВ		температура плавления компонента В
ТЕ		температура эвтектики
Е		точка эвтектики

На линии эвтектики DЕC в равновесии находятся три фазы:

• 
  расплав состава точки Е (L_E);
  
• 
  кристаллы твердого раствора α состава точки D (α_D);
  
• 
  кристаллы твердого раствора β состава точки C (β_C);
  

По достижении температуры эвтектики (Т_Е) наступает эвтектическая реакция – из расплава выделяются кристаллы обоих твердых растворов:

.

(3.16)

Рассмотрим процесс охлаждения расплава, заданного точкой М₁.

Точка	Что происходит	Ф	С	Что означает число степеней свободы
М1	Охлаждение расплава	1	2	Можно менять температуру и состав жидкой фазы
а	Появляются первые кристаллы твердого раствора β из расплава состава y0	2	1	Можно менять или температуру или состав расплава. Каждой температуре соответствует определенный состав жидкой и твердой фаз
b	Продолжается кристаллизация твердого раствора β состава y2из расплава состава y1	2	1	Можно менять температуру или состав расплава
е	Одновременно кристаллизуются твердый растворы α и β. Состав расплава остается постоянным yЕ. На кривой охлаждения наблюдается горизонтальный участок е-е’	3	0	Температура (ТЕ), состав твердых фаз и состав расплава постоянные
h	Продолжается охлаждение механической смеси твердых растворов α и β	2	1	Можно менять только температуру

Рассмотрим процесс охлаждения расплава, заданного точкой М2.

Точка	Что происходит	Ф	С	Что означает число степеней свободы
М2	Охлаждение расплава	1	2	Можно менять темпера- туру и состав расплава
с	Появляются первые кристаллы твердого раствора β	2	1	Можно менять или температуру или состав расплава
d	Исчезает последняя капля расплава	2	1	Можно менять только температуру
f	Охлаждение твердого раствора β	1	1	Можно менять только температуру
g	Образуются кристаллы твердого раствора α, в твердом растворе β уменьшается содержание компонента А	2	1	Каждой температуре соответствует определенный состав твердого раствора

Диаграммы состояния с ограниченной растворимостью компонентов в твердом состоянии с перитектикой (II типа).

Рассмотрим фазовую диаграмму образования твердых растворов с ограниченной растворимостью компонентов в твердом состоянии и с образованием перитектической смеси (рис. 3.10).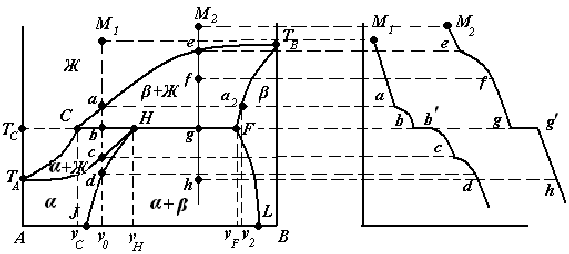

Рис. 3.10. Диаграмма состояния системы с ограниченной растворимостью компонентов в твердом состоянии с перитектикой
В этом случае один из твердых растворов устойчив только до определенной температуры (температуры перитектики Т_С).

Значение полей
Ж	расплав
α	кристаллы твердого раствора α
β	кристаллы твердого раствора β
α + Ж	расплав + кристаллы твердого раствора α
β + Ж	расплав + кристаллы твердого раствора β
α + β	механическая смесь кристаллов твердых растворов α и β
Значение линий
ТАС и СТВ	линии ликвидуса, каждая точка линий показывает состав расплавов, равновесных с кристаллами твердых растворов α и β соответственно
ТАH и ТВF	линии солидуса, каждая точка линий показывает составы твердых растворов α и β, находящихся в равновесии с расплавом
СНF	линия перитектики
НJ	каждая точка линии показывает состав кристаллов твердого раствора α, равновесного с кристаллами α + β (линия расслоения)
FL	каждая точка показывает состав кристаллов тв. раствора β, равновесного с кристаллами α + β (линия расслоения)
Значение точек
ТА	температура плавления компонента А
ТВ	температура плавления компонента В
ТС	температура перитектики
С	точка перитектики

На перитектической прямой СНF в равновесии находятся три фазы:

• 
  расплав состава точки С (L_С);
  
• 
  кристаллы твердого раствора α состава точки H (α_H);
  
• 
  кристаллы твердого раствора β состава точки F (β_F);
  

Для поддержания постоянного состава расплава при кристаллизации твердого раствора α, ранее выпавшие кристаллы твердого раствора β должны растворяться. При этом происходит перитектическое превращение:

.

(3.17)

Рассмотрим процесс охлаждения расплава, заданного точкой М₁.

Точка	Что происходит	Ф	С	Что означает число степеней свободы
М1	Охлаждение расплава	1	2	Можно менять температуру и состав расплава
а	Появляются первые кристаллы твердого раствора β состава y2из расплава состава y0	2	1	Каждой температуре соответствует состав жидкой и твердой фаз.
b	Кристаллизуются твердый раствор α состава yН, ранее выпавшие кристаллы твердого раствора β состава yFпереходят в расплав. Состав расплава остается постоянным yC. На кривой охлаждения горизонтальный участок b-b’	3	0	Температура (ТC), состав твердых фаз и состав расплава постоянные
c	Исчезает последняя капля расплава	2	1	Можно менять только температуру
d	Из кристаллов твердого раствора α образуются кристаллы твердого раствора β	2	1	Можно менять только температуру

Рассмотрим процесс охлаждения расплава, заданного точкой М₂.

Точка	Что происходит	Ф	С	Что означает число степеней свободы
М2	Охлаждение расплава	1	2	Можно менять температуру и состав расплава
е	Появляются первые кристаллы твердого раствора β	2	1	Можно менять или температуру или состав жидкой фазы
f	Продолжают выпадать кристаллы твердого раствора β	2	1	Можно менять или температуру или состав жидкой фазы
g	Исчезает последняя капля расплава, в результате перитектического превращения появляются кристаллы α, на кривой охлаждения горизонтальный участок g-g’	3	0	Температура (ТC), состав твердых фаз и состав расплава постоянные
h	Охлаждение механической смеси твердых растворов α и β	2	1	Можно менять только температуру

Системы с ограниченной взаимной растворимостью компонентов

в жидком состоянии
Растворы жидкостей в жидкостях очень разнообразны по своей природе и свойствам. Растворимость жидкостей в жидкостях зависит от природы растворителя и растворенного вещества, температуры, присутствия в растворе посторонних веществ. Существуют растворы с неограниченной взаимной растворимостью, ограниченной взаимной растворимостью и с практически полной взаимной нерастворимостью жидкостей.

Рассмотрим системы с ограниченной взаимной растворимостьюжидкостей. Ограниченная взаимная растворимость двух жидкостей наблюдается в системах со значительным отклонением от идеальной. Растворимость таких жидкостей зависит от температуры. В одних системах взаимная растворимость жидкостей с ростом температуры увеличивается (системы с верхней критической температурой растворения), в других уменьшается (системы с нижней критической температурой растворения).

Под критической температурой растворения понимают ту температуру, при которой составы двух равновесных жидких фаз одинаковы.

Для изображения зависимости взаимной растворимости жидкостей от температуры при постоянном давлении строят диаграммы состояния в координатах температура – состав (диаграммы растворимости). Такая диаграмма состояния для системы с верхней критической температурой растворения приведена на рис. 3.10. На этой диаграмме кривая akb, называемая кривой расслоения, делит диаграмму на две области: гомогенную,лежащую над кривой расслоения,и гетерогенную,находящуюся под кривой расслоения. Фигуративные точки внутри гомогенной области, например точка d, изображают состояние однофазной условно бивариантной системы (С_усл = 2 – 1 + 1= 2). Фигуративные точки, лежащие внутри гетерогенной области, например точка О, изображают состояние двухфазной условно моновариантной системы (С_усл = 2 – 2 + 1 = 1).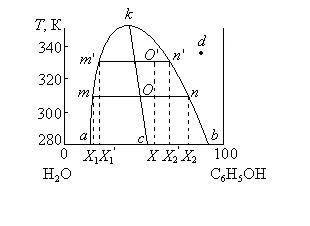



Рис. 3.11. Диаграмма растворимости системы вода-фенол с верхней критической температурой растворения при P = const
Составы равновесных жидких фаз определяются по правилу соединительной прямой, согласно которому фигуративные точки, изображающие состав всей системы в целом и составы отдельных равновесных фаз, лежат на одной прямой, называемой нодой (или коннодой), которая для двухкомпонентных систем параллельна оси состава. Так система состава X, изображенная на диаграмме точкой О (рис. 3.11), при температуре 310 К распадается на две равновесные жидкие фазы m и n состава X₁ и X₂. Характерной особенностью расслаивающихся систем является то, что с изменением состава всей системы при данной температуре составы отдельных равновесных фаз остаются неизменными, а изменяется только их количественное соотношение. С изменением температуры составы равновесных жидких фаз изменяются. Так, при повышении температуры от 310 до 330 К (рис. 3.10) состав слоя m изменяется от X₁ до X₁^′, а слоя n – от X₂ до X₂^′. При критической температуре растворения оба жидких раствора по составу тождественны, и система, изображенная на диаграмме точкой k, при Р = const является условно инвариантной (С_усл = 2 – 2 = 0).

Положение критической точки k на диаграмме определяется по правилу Алексеева: середины нод, расположенных между точками, изображающими составы равновесных жидких фаз при разных температурах, лежат на одной прямой, идущей от критической точки (прямая kc на рис. 3.10). Для большинства систем линия kc не перпендикулярна оси состава.
Системы с неограниченной взаимной растворимостью компонентов в жидком и твердом состояниях (изоморфные смеси)
Изоморфные смеси –это кристаллические фазы переменного состава,образованные двумя или более изоморфными компонентами. Под изоморфными компонентами понимают кристаллические вещества,аналогичные по химическому составу и по структуре, способные образовывать кристаллы смешанного состава. Основным признаком изоморфных веществ является способность их атомов или ионов к взаимному замещению с образованием твердых растворов.

Твердые растворы– гомогенные системы переменного состава, состоящие из двух или более компонентов.

В отличие от механической смеси твердый раствор является однофазным, состоит из одного вида кристаллов и имеет одну кристаллическую решетку. В отличие от химического соединения твердый раствор существует не при строго определенном соотношении компонентов, а в интервале концентраций.

Строение твердых растворов на основе одного из компонентов системы таково, что в кристаллическую решетку одного компонента входят атомы другого компонента системы. Различают твердые растворы трех типов: внедрения, замещения и вычитания.

Твердые растворы внедрения– растворы, при кристаллизации которых частицы (атомы, молекулы или ионы) одного компонента размещаются между узлами кристаллической решетки другого компонента. Они могут образовываться лишь при условии, что размеры частиц компонента, растворяющегося путем внедрения, невелики. Так, в металлических сплавах диаметр атома растворяемого вещества обычно не превышает 0,6 диаметра атома основного металла – растворителя (растворение в металлах неметаллов – бора, углерода, водорода, азота).

По мере накопления внедряемого вещества устойчивость кристаллической решетки растворителя уменьшается. Поэтому концентрация растворяемого вещества не может быть выше некоторого предела – ограниченная растворимость.

Твердые растворы замещения– растворы, при кристаллизации которых частицы (атомы или ионы) растворяемого вещества замещают в узлах кристаллической решетки частицы растворителя. Для образования твердых растворов замещения необходимо, чтобы кристаллические структуры замещающего и замещаемого компонентов были достаточно близки, и чтобы радиусы атомов или ионов компонентов различались не очень сильно. При этих условиях замещение не вызывает чрезмерных напряжений в кристаллической решетке и устойчивыми могут быть твердые растворы любого состава. Таким образом, компоненты бинарной смеси, образующие твердые растворы замещения, могут быть неограниченно растворимы один в другом, и образовывать непрерывный ряд твердых растворов от 0 до 100% каждого из компонентов. Примером таких растворов может служить система AgCl-NaCl. Кристаллическая решетка обоих компонентов – кубическая гранецентрированная, длина ребра куба элементарной ячейки AgCl составляет 5,56 Ǻ, у NaCl5,63 Ǻ; радиусы ионов серебра и натрия соответственно равны 1,13 Ǻ и 0,98 Ǻ.

Твердые растворы вычитания– растворы, образование которых связано с дефектами структуры, в которой имеются вакантные (не занятые) места.

Необходимо подчеркнуть, что в твердом растворе внедренные или замещенные атомы располагаются в хаотическом беспорядке. Об их равномерном распределении во всем кристалле можно говорить только в статистическом смысле, т.е. сопоставляя объемы, содержащие достаточно большое число кристаллических ячеек.

Для систем с неограниченной взаимной растворимостью компонентов как в жидком, так и в твердом состоянии известны три типа диаграмм плавкости, примеры которых приведены на рис. 3.12–3.14. Области существования и равновесные фазы указаны на диаграммах. Твердыми фазами в таких двухкомпонентных системах являются твердые растворы с неограниченной растворимостью компонентов в твердом состоянии. Характерной особенностью диаграмм плавкости таких систем является отсутствие эвтектик. На этих диаграммах верхние кривые – линии ликвидуса, нижние кривые – линии солидуса. В системах первого типа (рис.3.12) при увеличении концентрации компонента В в расплаве температура начала кристаллизации из него твердого раствора непрерывно повышается. Линия ликвидуса имеет вид непрерывной кривой, все точки которой лежат между температурами кристаллизации чистых компонентов А и В.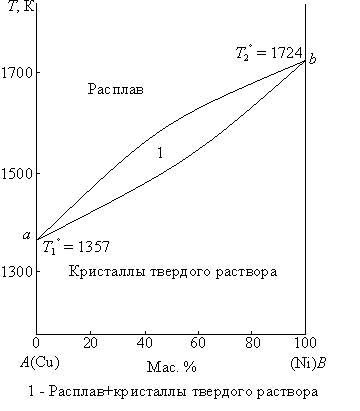



Рис. 3.12. Диаграмма плавкости системы Cu – Ni при Р = const:

1 – расплав + кристаллы твердого раствора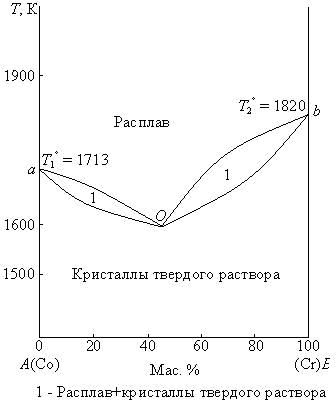


Рис. 3.13. Диаграмма плавкости системы Co – Cr при Р = const:

1 – расплав + кристаллы твердого раствора
В системах второго типа (рис. 3.13) температура начала кристаллизации твердого раствора из расплава понижается при добавлении одного компонента к другому до точки О на линии ликвидуса, имеющей вид непрерывной кривой, проходящей через максимум, а затем повышается.

В системах третьего типа (рис. 3.14) температура начала кристаллизации твердого раствора из расплава повышается при добавлении одного компонента к другому до точки О на линии ликвидуса, имеющей вид непрерывной кривой, проходящей через максимум, а затем понижается.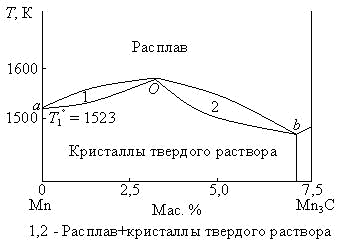



Рис. 3.14. Диаграмма плавкости системы Mn – C при Р = const:

1, 2 – расплав + кристаллы твердого раствора
При кристаллизации из расплава твердого раствора в большинстве случаев изменяется состав как расплава, так и твердого раствора. Согласно первому правилу Гиббса – Розебома, твердый раствор по сравнению с жидким расплавом, находящимся с ним в равновесии, богаче тем компонентом, прибавление которого к расплаву приводит к повышению температуры начала кристаллизации твердого раствора. В соответствии со вторым правилом Гиббса – Розебома в точках минимума и максимума на кривых температур плавления (кристаллизации) твердый раствор и находящийся с ним в равновесии жидкий расплав имеют одинаковый состав. Система, изображенная на диаграмме плавкости фигуративной точкой O (рис. 12, 13), при Р = const условно инвариантна (С_усл = 2 – 2 = 0).

Системы с неограниченной взаимной растворимостью компонентов в жидком и твердом состояниях встречаются довольно часто. Наиболее распространенными являются системы первого и второго типа. Примерами систем первого типа могут служить системы Ag – Аu, Со – Ni, Fe – Co, Mo – W, РbСl₂ – SnCl₂. Примерами систем второго типа являются системы Аu – Сu, Со – Сr, Мn – Ni, KCl – КВr, СаСl₂ – SnCl₂.