ЛАБОРАТОРНЫЙ ПРАКТИКУМ ПО ХИМ ТЕРМОДИНамиКЕ. Практикум по химической термодинамике учебное пособие для студентов всех специальностей

• Название: Практикум по химической термодинамике учебное пособие для студентов всех специальностей
• Анкор: ЛАБОРАТОРНЫЙ ПРАКТИКУМ ПО ХИМ ТЕРМОДИНамиКЕ.doc
• Дата: 19.05.2017
• Размер: 2.28 Mb.
• Имя файла: ЛАБОРАТОРНЫЙ ПРАКТИКУМ ПО ХИМ ТЕРМОДИНамиКЕ.doc
• Тип: Практикум; #7896
• страница: 8 из 15

3. ФАЗОВЫЕ РАВНОВЕСИЯ

3.1. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

Физико-химические системы подразделяются на гомогенные и гетерогенные.

Гомогенной называется система, внутри которой нет поверхностей раздела, отделяющих различающиеся либо по физическому строению, либо по химическим свойствам, части системы. Примерами таких систем могут служить: смесь газов, ненасыщенный раствор соли в воде, кристаллы чистого вещества.

Гетерогенной называется система,состоящая из различных по своимфизическим или химическим свойствам частей, отделенных друг от друга поверхностями раздела. Примерами гетерогенных систем могут служить: смесь кристаллических веществ, смесь нескольких жидкостей, ограниченно растворимых друг в друге, насыщенный раствор соли в воде с избытком твердой соли.

Любая гетерогенная система состоит из нескольких фаз. Фазой называется гомогенная часть системы, ограниченная поверхностью раздела и характеризующаяся одинаковыми химическими и физическими свойствами во всех своих точках. По числу фаз (Ф) различают системы однофазные, двухфазные, трехфазные и т. д.

Каждая система состоит из одного или нескольких веществ. Индивидуальные химические вещества, которые могут быть выделены из системы простыми препаративными методами (кристаллизация, осаждение, испарение и др.) и существовать вне ее самостоятельно, называются составляющими веществами системы. Например, в водном растворе хлорида натрия составляющими веществами являются NaCl и Н₂О, а ионы Na⁺ и С1⁻ ими не являются.

Составляющие вещества, с помощью наименьшего числа которых можно однозначно выразить состав каждой фазы при любых условиях существования системы, называются компонентами.

Если в системе между составляющими веществами нет химического взаимодействия, то число компонентов равно числу составляющих веществ. При наличии химического взаимодействия число компонентов находится как разность между числом составляющих веществ и числом уравнений, связывающих равновесные концентрации этих веществ. В зависимости от способа образования равновесной системы и условий ее существования при одном и том же числе составляющих веществ число компонентов может быть разным.

Например, равновесная газообразная система, содержащая азот, водород и аммиак, может быть получена двумя путями:

N2 + 3H2 ↔2NH3	(3.1)
2NH3 ↔ N2 + 3H2	(3.2)

В первом случае, если азот и водород взяты в исходной системе в произвольном соотношении, равновесные концентрации или пропорциональные им относительные парциальные давления всех трех составляющих веществ связаны между собой только одним уравнением:

(3.3)

где ; – парциальное давление i-ого компонента; –стандартное давление,равное1,01325·10⁵Па.В этом случае числокомпонентов в системе равно двум.

Во втором случае равновесные концентрации или относительные парциальные давления трех составляющих веществ связаны между собой двумя уравнениями:

	(3.4)
	(3.5)

В этом случае число компонентов в системе равно единице.

При подсчете числа компонентов в системе учитываются уравнения, связывающие равновесные концентрации или пропорциональные им относительные парциальные давления, но не числа молей составляющих веществ. Это особенно следует иметь в виду, если система гетерогенная.

Например, в системе, состоящей из СаСО_3(тв), СаО_(тв) и CO_2(газ), при равновесии, описываемом уравнением:

СаСО3(тв) ↔ СаО(тв) + CO2(газ)

(3.6)

закон действующих масс имеет вид:

(3.7)

В рассматриваемой равновесной системе число молей СаО_(тв) равно числу молей CO_2(газ), но (– относительное парциальное давление паров СаО над твердым СаО). В такой системе число компонентов не может быть меньше двух.

По числу компонентов (К) различают системы однокомпонентные, двухкомпонентные, трехкомпонентные и т. д.

Любая система обладает определенными свойствами. Термодинамические свойства, наименьшее число которых необходимо для описания состояния данной системы, называются параметрами состояния.В качестве параметров состояния выбираются такиетермодинамические свойства, которые легко могут быть измерены экспериментальным путем. К таким свойствам относятся температура, давление, объем, концентрация. Концентрация обычно выражается в массовых или молярных процентах или долях.

Число независимых термодинамических параметров состояния фаз равновесной системы, произвольное изменение которых в определенных пределах не вызывает исчезновения одних и образования других фаз, называется числом термодинамических степеней свободы, или вариантностью системы.

По числу степеней свободы (С) системы разделяются на инвариантные, или нонвариантные (С = 0), моновариантные (С = 1), бивариантные, или дивариантные (С = 2) и т. д. В равновесной системе связь между числами фаз, компонентов и термодинамических степеней свободы выражается законом равновесия фаз – правилом фаз Гиббса:

С = К – Ф + 2.

(3.8)

Цифра 2 в уравнении (3.8) свидетельствует о влиянии на систему двух внешних параметров – давления и температуры. В частных случаях, когда из внешних факторов на систему оказывает влияние только давление (T = const) или температура (р = const), число степеней свободы уменьшается на единицу и правило фаз принимает вид:

Сусл = К – Ф + 1.

(3.9)

Вариантность системы в этом случае называется условной (С_усл), а система – условно инвариантной, условно моновариантной и т. д. При постоянстве давления и температуры

Сусл = К – Ф.

(3.10)

Если в рассматриваемой системе составы двух равновесных фаз, выраженные в массовых или молярных процентах или долях, одинаковы, например, состав жидкой фазы одинаков с составом пара, то при подсчете числа степеней свободы вместо уравнения (3.8) следует пользоваться уравнением

Сусл = К – Ф +2 – 1 = К – Ф + 1,

(3.11)

а вместо уравнения (3.9) уравнением

Сусл = К – Ф + 1 – 1 = К – Ф.

(3.12)

В некоторых случаях состояние системы определяется и такими внешними факторами как электрический потенциал, магнитное поле, поле тяготения и др., которые также следует учитывать при подсчете числа степеней свободы в равновесной системе. В общем случае, когда на систему действуют n различных внешних факторов, уравнение имеет вид:

С = К – Ф + n.

(3.13)

Из уравнения (3.13) следует, что число степеней свободы возрастает с увеличением числа независимых компонентов и уменьшается при росте числа фаз.

Правилу фаз Гиббса не подчиняются коллоидные системы, в которых дисперсная фаза микроскопических размеров. Правило фаз не применимо к неравновесным метастабильным состояниям (переохлажденная вода, перегретый пар и т.д.).
Фазовые диаграммы состояния систем
Для графического изображения фазовых равновесий в системе пользуются диаграммами состояния, построенными в координатах свойство-состав. В качестве изучаемых свойств могут быть выбраны тепловые, объемные, электрические, магнитные, оптические и другие свойства. Диаграмма– совокупность геометрических элементов (точек, линий, плоскостей и т.д.), которые изображают связь между параметрами, определяющими состояние системы и ее составом. С помощью диаграмм состояния можно установить протекающие в системе качественные изменения, характер взаимодействия между компонентами, области существования и составы равновесных фаз и т. д. В основе анализа диаграмм состояния лежат два положения, сформулированные Н.С. Курнаковым: принцип непрерывности и принцип соответствия.

Согласно первому принципу, при непрерывном изменении параметров, определяющих состояние системы, свойства отдельных фаз изменяются также непрерывно, свойства же всей системы изменяются непрерывно лишь до тех пор, пока не меняется число или природа ее фаз. При исчезновении старых или появлении новых фаз свойства системы изменяются скачкообразно.

Согласно принципу соответствия, на диаграмме состояния при равновесии каждому комплексу фаз и каждой фазе в отдельности соответствует свой геометрический образ: плоскость, линия, точка.

Одной из задач физико-химического анализа является построение диаграмм состояния двойных, тройных и более сложных систем, изображающих зависимость между свойством (температурой) и составом. Интерес и важность исследования подобных диаграмм состояния заключается не только в установлении наличия фаз в системе, но также выяснении природы и характера взаимодействия между компонентами системы, насколько это возможно, на основании изучения вида полученных диаграмм.

Вид диаграммы состояния зависит от числа компонентов в системе.

Для построения фазовых диаграмм используют различные экспериментальные методы, наиболее эффективным из которых является метод физико-химического анализа. В основе физико-химического анализа лежит изучение функциональной зависимости между значениями какого-либо физического свойства системы и факторами, определяющими ее равновесие. Наиболее общим современным способом определения равновесия между твердыми и жидкими фазами при некоторых температурах является метод термического анализа (термография).

Метод термического анализа (термография) – совокупность экспериментальных методов определения температуры, при которой в равновесной системе изменяется число фаз. Сущность метода термического анализа заключается в том, что процессы, протекающие в веществе и сопровождающиеся тепловым эффектом, приводят к появлению изотермических остановок или изменения угла наклона кривой температура – время.

Различают: визуальный термический анализ (простая термография) и термический анализ, основанный на построении кривых охлаждения (дифференциальная термография). Метод построения кривых охлаждения(Н.С.Курнаков) основан на том, что пока в охлаждаемой системе не происходит никаких превращений, температура падает равномерно. Появление или исчезновение фаз сопровождается тепловыми эффектами, на кривой охлаждения появляются перегибы или происходит температурная остановка. Таким образом, по изломам на кривых охлаждения можно судить об изменении фазового состава исследуемой смеси (рис. 3.1).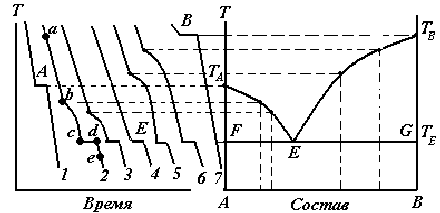

Рис. 3.1. Построение диаграммы плавкости двухкомпонентной системы

по кривым охлаждения
Если медленно охлаждать чистое расплавленное вещество (кривые 1 и 7 на рис. 3.1), то его кристаллизация вызовет температурную остановку, так как выделяющаяся скрытая теплота кристаллизации будет компенсировать отвод теплоты в окружающую среду. Поэтому на кривой охлаждения появляется горизонтальный участок. Размер горизонтального участка, т.е. длительность температурной остановки, зависит от количества вещества и от скорости охлаждения системы. Состав жидкой фазы при кристаллизации чистого вещества не изменяется, поэтому температура кристаллизации постоянна. Подобную кривую охлаждения дает смесь эвтектического состава (кривая 4).

Несколько сложнее кривые охлаждения смесей различного состава (кривые 2, 3, 5, 6). В этом случае до начала кристаллизации температура падает со временем практически линейно (участок ab,кривая 2). Однако, смесь в отличие от чистого вещества, кристаллизуется не при постоянной температуре (хотя процесс также является экзотермическим), а в некотором температурном интервале. Это обусловлено тем, что при выделении кристаллов одного из компонентов смесь обогащается вторым, и температура ее кристаллизации понижается. Поэтому на кривых охлаждения при температуре начала кристаллизации (точка b, кривая 2) происходит лишь излом кривой, так как скорость охлаждения уменьшается в результате выделения теплоты кристаллизации (участок bc, кривая 2).

Температура падает до тех пор, пока состав сплава (смеси) не станет эвтектическим (точка c). С этого момента будет кристаллизоваться эвтектика(мелкозернистая смесь кристаллов двух компонентов) при постоянной температуре (участок cd). В точке d расплав полностью исчезает и начинается охлаждение твердых фаз (участок de, кривая 2).

В результате исследования чистых веществ и нескольких смесей с различными содержаниями компонентов получают серию кривых охлаждения. Затем строят диаграмму плавкости системы, откладывая по оси ординат температуру плавления (кристаллизации) чистых веществ, смесей (сплавов), а по оси абсцисс - состав в массовых, атомных и т.д. процентах, т.е. содержание одного из компонентов.

Точки А, В на диаграмме соответствуют 100%-ному содержанию компонентов А и В соответственно. Отсчет содержания компонента В начинается от точки А, где его содержание составляет 0%.

Построение фазовых диаграмм состояния является тонким и трудоемким исследованием. Однако большая ценность полученных с их помощью результатов вполне оправдывает затраченный труд. В минералогических системах диаграммы состояния позволяют судить о внутренней структуре минерала, об образовании различных соединений между компонентами и их составе, об образовании смешанных кристаллов, полиморфных превращениях и многих других особенностях внутреннего строения минерала.
Однокомпонентные системы
Состояние однокомпонентной системы вполне определяется двумя независимыми параметрами, например, давлением и температурой, а объем системы является функцией давления и температуры V = f (P,T). Если по трем координатным осям отложить, соответственно, давление, температуру и объем системы, то полученная пространственная диаграмма, выражающая зависимость состояния системы и фазовых равновесий в ней от внешних условий, называется диаграммой состояния, или фазовой диаграммой. Построение таких диаграмм связано с трудностями, и они мало удобны для практического применения. Поэтому чаще используют плоские фазовые диаграммы, являющиеся проекциями пространственной диаграммы на плоскость Р–Т, V–Т, Т–V. На плоской диаграмме состояния каждой фазе отвечает своя область, представляющая собой совокупность так называемых фигуративных точек, изображающих состояния равновесной системы. Равновесия двух фаз на диаграмме изображаются линиями пересечения областей, а равновесия трех фаз – точкой пересечения этих линий, называемой тройной точкой. По диаграмме состояния можно установить число фаз, их химическую природу и границы существования фаз.

Состояние воды изучено в широком интервале температур и давлений. При высоких давлениях установлено семь кристаллических модификаций льда. На рис. 3.2 приведена плоская диаграмма состояния воды при невысоких давлениях (Р < 2,03^.10⁷ Па).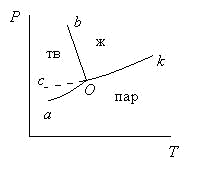




Рис. 3.2. Диаграмма состояния воды при низких давлениях
Наклон линии плавления Оb отличается от линий плавления большинства других систем, что объясняется уменьшением объема при плавлении льда. На рисунке линия сО соответствует равновесию между переохлажденной водой и паром, которое является неустойчивым, метастабильным. Перегреть кристаллическое вещество не удается, так как происходит разрушение решетки, поэтому линия возгонки аО заканчивается в тройной точке О. При отсутствии воздуха тройной точке воды соответствует Т = 273,16К и Р = 610,48Па.Температура,равная273,16К,принятав качестве единственной реперной точки (точки отсчета) для абсолютной термодинамической температурной шкалы Кельвина. При атмосферном давлении (Р = 1,0133^.10⁵ Па) температура льда на 0,01 К ниже тройной точки (Т = 273,15 К = 0^о С). Линия аО – линия возгонки, kО – линия испарения.