VBA-методичка. Практикум по информатике для студентов очной формы обучения Часть ii. Visual Basic for Applications
 Скачать 0.95 Mb.
|
Вариант 1. Отладку программы выполнить на примере, приведенном в таблице.Вариант 2. Программу отладить на примере, в котором измерены правые углы.Исходные данные этого примера. Столбец 1: 1, 2, 3, 4, 5, 6.Столбец 2: 122, 98, 153, 90, 203, 52. Столбец 3: 28, 8, 27, 1, 12, 46.Столбец 9: 301.77, 284.67, 254.52, 318.33, 242.37, 524.88. Значения для первой точки в столбцах 6,7,14,15: 163, 17, 461.83, 235.49.2. Разработка приложения “Прямая геодезическая задача” На листе Excel разместить таблицу, содержащую 5 столбцов с именами: N-номер пункта, A-дирекц. угол (град.), d-гориз. Пролож. до след. пункта, X, Y -координаты. Ввести данные тестового примера (для 3-7 пунктов) в столбцы N,A,d, а для первого пункта - и в столбцы X,Y. Программа должна вычислять координаты X,Y остальных пунктов. Рекомендации. На листе Excel разместить переключатели (Option Buttons) с надписями (свойство Caption) Левые углы и Правые углы, а еще правее кнопку с надписью Вычислить. Кнопке должна соответствовать событийнаяпроцедура вычисления координат пунктов. Программу надо отладить на примерах, когда измерены левые и правые углы. 3. Разработка приложения “Обратная геодезическая задача” Задача аналогична предыдущей (см. работу 2), только заданными являются столбцы N, X, Y, а вычислить надо дирекционные углы и горизонтальные проложения в столбцах A, d. 4. Разработка приложения “Преобразование географических координат в прямоугольные и прямоугольных в географические” Э   Y-500 та курсовая работа особенно полезна для студентов, будующая специальность которых имеет отношение к наукам о Земле (геология, геодезия, экология, горное дело и т.п.). Но, вообще говоря, представлять системы координат, в которых строятся различные карты, должен каждый образованный человек. Известно, что в качестве геометрической модели Земли используют эллипсоид. В России обычно применяют параметры эллипсоида Красовского: a 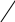 = 6 378 245.000 м - большая полуось,b = 6 356 863.019 м - малая (полярная) полуось, e   X 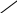 12 = 0.006 693 4216 – квадрат первого эксцентриситета, e22 = 0.006 719 2188 – квадрат второго эксцентриситета. Д  ля перехода к прямоугольным координатам эллипсоид (как дыню) разрезают от полюса к полюсу на шестиградусные зоны (дольки). Каждая зона-долька как-бы распрямляется – делается плоской. Координата X отсчитывается от экватора, а Y – от осевого меридиана зоны с добавлением 500 км. Эта добавка к координате Y служит для того, чтобы координаты Y были положительными. Таким образом, в каждой зоне свои координаты Y, отсчитываемые от своего осевого меридиана.Каждая шестиградусная зона делится еще параллелями через 4 градуса, и получаются листы, для которых строятся карты масштаба 1:1000000 (в 1 см 10 км). Каждый лист миллионного масштаба делится на 36 листов масштаба 1:200000 или на 144 листа масштаба 1:100000 (в 1 см 1 км) – так строятся карты в прямоугольных координатах. Обозначим широту точки через LT (Latitude – широта), а долготу – через LN (Longitude – долгота). С формулами для расчета X, Y по известным значениям LT, LN при заданном осевом (центральном) меридиане CM можно познакомиться по указанным в конце этой работы книгам. Вместо формул, здесь просто приведем начало модуля, содержащего общую процедуру LTLNtoXY, пересчитывающую географические координаты в прямоугольные, и опишем постановку остальных задач, которые надо запрограммировать, чтобы завершить разработку приложения. Option Explicit Const Pi180 As Double = 0.0174532925 Const A As Double = 6378245 Const B As Double = 6356863.019 Const EE1 As Double = 0.0066934216 Const EE2 As Double = 0.0067192188 Private Sub LTLNtoXY(LT As Double, LN As Double, X As Double, Y As Double, CM As Double) ' LT – ШИPOTA (радианы) ' LN – ДOЛГOTA (радианы) ' CM - ОСЕВОЙ MEPИДИAH (градусы) ' X, Y – KOOPДИHATЫ (км) Dim N As Double, DL As Double, S As Double, DL2 As Double, T As Double, T2 As Double Dim SINLT As Double, COSLT As Double, COS2 As Double, COS3 As Double, COS5 As Double Dim A2 As Double, A4 As Double, B1 As Double, B3 As Double, B5 As Double, T4 As Double DL = LN - CM * Pi180: DL2 = DL * DL SINLT = Sin(LT): COSLT = Cos(LT): T = SINLT / COSLT T2 = T * T: T4 = T2 * T2 COS2 = COSLT * COSLT: COS3 = COSLT * COSLT * COSLT: COS5 = COS2 * COS3 N = A / Sqr(1 - EE1 * SINLT * SINLT) S = 6367558.49587 * LT - 16036.48027 * Sin(2 * LT) + _ 16.828067 * Sin(4 * LT) - 0.021975 * Sin(6 * LT) A2 = N * SINLT * COSLT / 2: A4 = N * SINLT * COS3 * (5 - T2) / 24 B1 = N * COSLT: B3 = N * COS3 * (1 - T2 + EE2 * COS2) / 6 B5 = N * COS5 * (5 - 18 * T2 + T4) / 120 X = ((A2 + A4 * DL2) * DL2 + S) * 0.001 Y = ((B3 + B5 * DL2) * DL2 + B1) * DL * 0.001 + 500 End Sub Для построения приложения (назовем его Координаты.xls) на листе Excel в первой строке поместим названия столбцов таблицы: Номер точки, LT, LN, X, Y, Число итераций. Введем в ячейки второй и следующих строк номера нескольких точек и их географические координаты в градусах и поместим на лист Excel элементы управления, как показано ниже:
Поясним элементы управления, событийные и общие процедуры. Поле с именем TextBox1 (имена элементов управления на листе Excel не показаны) предназначается для ввода значения осевого меридиана – в нашем примере 105о. Командные кнопки c именами BTN1 и BTN2 инициируют исполнение событийных процедур BTN1_Click и BTN2_Click. Первая из них из каждой непустой строки таблицы (начиная со строки 2) извлекает географические координаты LT, LN, переводит их из градусов в радианы и обращается к общей процедуре LTLNtoXY, текст которой приведен выше. Вычисленные координаты X,Y процедура BTN1_Click заносит в столбцы 4, 5 таблицы Excel. Событийная процедура BTN2_Click похожа на процедуру BTN1_Click, только исходные данные она берет из столбцов 4, 5 таблицы, а результаты помещает в столбцы 2, 3. Для вычисления значений LT, LN по известным прямоугольным координатам X, Y она обращается к общей процедуре XYtoLTLN, которая вычисляет географические координаты в следующей последовательности: устанавливается счетчик итераций K=0; задается первое приближение, например, LT = 56 ∙ Pi180, LN = CM ∙ Pi180, где Pi180 – константа для перевода градусов в радианы, CM – осевой (центральный) меридиан; путем обращения к процедуре LTLNtoXY находятся координаты XX, YY, соответствующие LT, LN; наращивается на 1 счетчик итераций и вычисляются невязки DX = X - XX, DY = Y – YY, DXY = DX2 + DY2 , а также новые значения широты и долготы LT = LT + DX ∙ 1000 / a, LN = LN + DY ∙ 1000 /a / cos(LN); если DXY < 0.0000001 , то задача считается решенной; в противном случае проверяется значение счетчика итераций; если K< 20, то управление передается блоку 3; иначе считается, что процесс не сходится (это может быть, если заданы нереальные для Земли координаты X,Y), и в качестве результатов условно присваиваются значения LT = 0, LN = 0. Обе событийные и общую процедуру XYtoLTLN надо разработать, а в событийной процедуре BTN2_Click также предусмотреть занесение в столбец 6 таблицы числа итераций, за которое сошелся процесс. Для проверки этой процедуры, можно очистить столбцы 2, 3 таблицы и нажать вторую командную кнопку – мы вновь должны получить исходные географические координаты. Литература к курсовой работе 4. Ломтадзе В.В. Программное обеспечение обработки геофизических данных. Л.: Недра, 1982. –280 с. Ломтадзе В.В. Программное и информационное обеспечение геофизических исследований. М.: Недра, 1993. –268 с. Справочник геодезиста (в двух книгах). Книга 1. М.: Недра, 1975. –544 с. ЛИТЕРАТУРА Абрамов С.А., Гнездилова Г.Г., Капустина Е.Н., Селюн М.И. Задачи по программированию. -М.: Наука. Гл. ред. физ.-мат. лит., 1988. -224 с. Гарнаев А.Ю. Самоучитель по VBA. -СПб: БХВ - Санкт-Петербург, 1999. -512 с. Ломтадзе В.В., Шишкина Л.П. Информатика: Учебное пособие. -Иркутск: Изд-во Иркутского госуд. технич. ун-та, 1999. -116 с. Пол Санна и др. Visual Basic для приложений (версия 5) в подлиннике: пер. с англ. –СПб.: BHV-Санкт-Петербург, 1999. -704 с. Численные методы. Учебник для техникумов. М., "Высш. Школа", 1976. -368 с. |