VBA-методичка. Практикум по информатике для студентов очной формы обучения Часть ii. Visual Basic for Applications
 Скачать 0.95 Mb.
|
По коэффициентам системы составляют расширенную матрицу a11 a12 …a1n a1,n+1 a21 a22 … a2n a2,n+2 (1.1) ….......................... an1 an2 … ann an,n+1 Одним из методов решения систем линейных алгебраических уравнений является метод последовательного исключения неизвестных (метод Гаусса), который состоит из двух этапов. 1 этап - исключение переменных Переменную x1 исключают из 2, 3, … , n-го уравнения . Переменную x2 исключают из 3, … , n-го уравнения и т.д. Наконец, переменную xn-1 исключают из n-го уравнения. Для исключения, допустим, переменной xk из i-го уравнения, необходимо сначала определить множительный коэффициент C=aik/akk , как отношение элементов k-го столбца, расположенных в i-ой и k-ой строках. Далее каждый элемент i-ой строки изменяется путем вычитания соответствующего элемента k-ой, умноженного на коэффициент С, т.е. aij=aij-akj*C. В результате таких преобразований элемент aik получит значение 0, а остальные элементы изменятся.В процессе исключения переменных изменяются элементы расширенной матрицы, и она приобретает следующий вид: a11 a12 …a1n a1,n+1 0 a[1]22 … a[1]2n a[1]2,n+2 ….......................... (1.2) 0 0 … a[n-1]nn a n-1]n,n+1 В квадратных скобках указано количество преобразований элементов расширенной матрицы. 2 этап - нахождение корней системы По элементам последней строки матрицы (1.2) можно найти значение . Значение корня xn используется для нахождения значения xn-1 по элементам (n-1)-ой строки и найденные корни xk+1, xk+2, … , xn будет найдено как  В работе используйте кнопку метод Гаусса, счетчик и поле для ввода n – количества неизвестных. Матрицу коэффициентов расположите на листе Excel. Зарезервируйте два массива. В первый массив копируете матрицу, во втором выполняете исключение очередного неизвестного, а затем заменяете первую матрицу. Корни уравнения выводите на лист Excel. Решите следующую систему уравнений: 2x1+3x2+7x3+6x4=1 3 x1+5 x2+3 x3+ x4=3 5 x1+3 x2+ x3+3 x4=4 3 x1+3 x2+ x3+6 x4=5 9. Приближенные методы решения систем алгебраических уравнений Наиболее распространенным приближенным методом решения является метод Зейделя. Суть метода заключается в том, что каждое уравнение разрешается относительно своей k-ой переменной и это значение считается новым приближением этой переменной, т.е.  О  собенностью этого метода является то, что для нахождения  используют уже уточненные значения  Разность между двумя соседними приближениями запоминается в элементах массива Tk= - |. Процесс поиска заканчивается, если все значения Tk окажутся меньше некоторой малой величины . В работе используйте кнопку – метод Зейделя, счетчик и поле для ввода n – количество неизвестных, поле для ввода . Матрицу коэффициентов располагаете на листе Excel. Корни уравнения выводите на лист Excel. Начальное приближение  задаете в ячейках листа.Решите следующую систему уравнений: 2x1+3x2+7x3+6x4=1 3 x1+5 x2+3 x3+ x4=3 5 x1+3 x2+ x3+3 x4=4 3 x1+3 x2+ x3+6 x4=5 Литература Н.И. Данилина, Н.С. Дубровская и др. «Численные методы». Высшая школа 1976г. 10. Интерполяция функций, заданных таблично Для исследования систем автоматического управления с нелинейными элементами, характеристики которых заданы в виде таблицы значений и моделирования таких характеристик на ЭВМ, применяются методы интерполяции. Эти методы позволяют подобрать полином, описывающий нелинейную зависимость, представленную таблично. Интерполяция – это подбор полинома m-ой степени, обеспечивающий прохождение функции через узловые точки. Количество узловых точек должно быть m+1. Метод Лагранжа Полином, формируемый методом Лагранжа, имеет вид Pm(x)=Y1B1(x)+Y2B2(x)+…+Ym+1Bm+1(x), где Bj(x) – многочлен m-ой степени. Многочлены Bj(x) могут принимать только два значения – либо 0, либо 1. 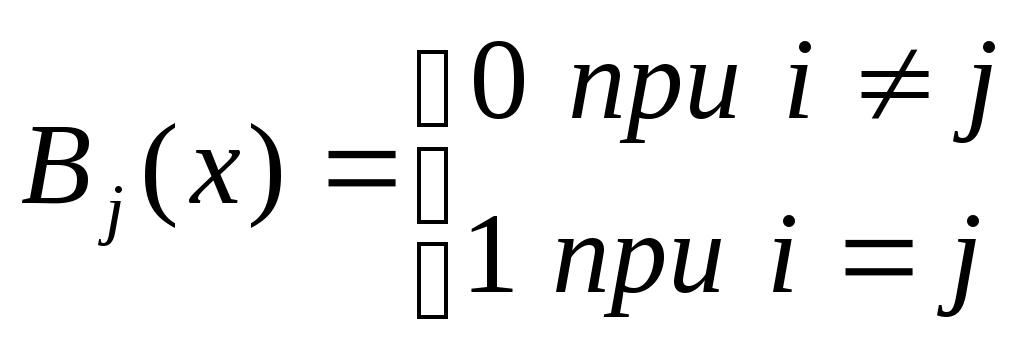 Полином в этом случае примет вид  Полином формируется сразу после ввода исходных данных для любой контрольной точки. В работе используйте кнопку – метод Лагранжа, счетчик и поле для ввода m – степень полинома, счетчик и поле для ввода Kkt – количество контрольных точек. Координаты узловых точек (X1 ,Y1)… (Xm+1 ,Ym+1) и значения контрольных точек (Xk) вводятся в колонки листа Excel. Для каждой контрольной точки вычисляется значение полинома. Функция f(x) задана таблично:
Значения контрольных точек выбрать самостоятельно. 11. Допольнительные курсовые работы для студентов горно-геологических специальностей1. Вычисление координат замкнутого теодолитного хода На горизонтально ориентированном листе Excel разместить таблицу - ведомость вычислений. В нее занести исходные данные - столбцы 1,2,3,9 и данные в первой строке столбцов 6,7,14,15. В первой (широкой) строке, справа от заголовка, разместить переключатели (Option Buttons) с надписями (свойство Caption) Левые углы и Правые углы, а еще правее кнопку с надписью Вычислить. Кнопке должна соответствовать событийнаяпроцедура вычисления координат замкнутого теодолитного хода. В результате вычислений должны быть последовательно заполнены пустые ячейки таблицы. Невязки углов и приращений координат до и после уравнивания разместить в соответствующих столбцах, под таблицей, пропустив одну строку. В приведенном примере измерены левые углы.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||