|
|
VBA-методичка. Практикум по информатике для студентов очной формы обучения Часть ii. Visual Basic for Applications
yy
  
X0=a x1 xn-1 b=xn x
Если же в качестве ξi выбирать правый конец отрезка Δxi , то приближенное значение интеграла равно площади ступенчатой фигуры, ограниченной сверху пунктирной линией и считается по формуле правых прямоугольников:
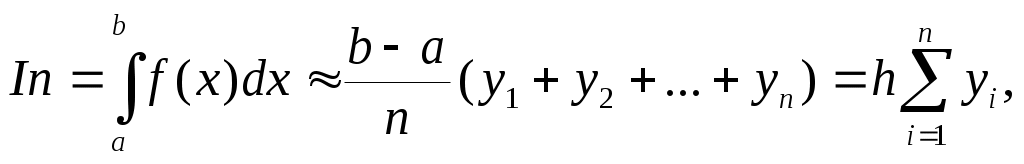
Интегрирование по методу трапеций М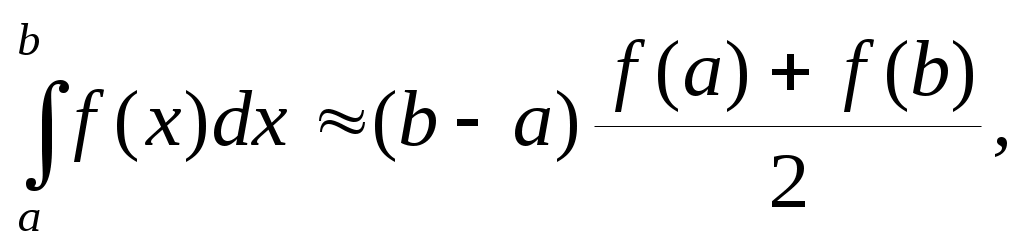
етод трапеций заключается в том , что на отрезке [a,b] дуга AB графика подинтегральной функции y=f(x) заменяется стягивающей ее хордой и вычисляется площадь трапеции Abba.
 Точность вычислений возрастает, если отрезок [a,b] разделить на несколько частей и применить формулу к каждому отрезку Δxi . Тогда
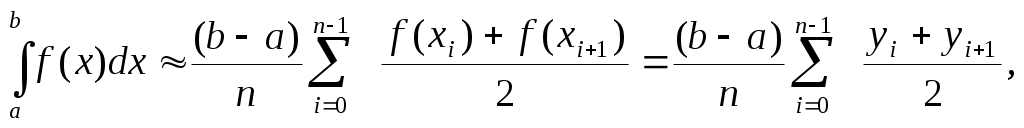
Так как под знаком суммы величины yi встречаются дважды (от i =1 до i =n-1), то последнее равенство можно записать в следующем виде:
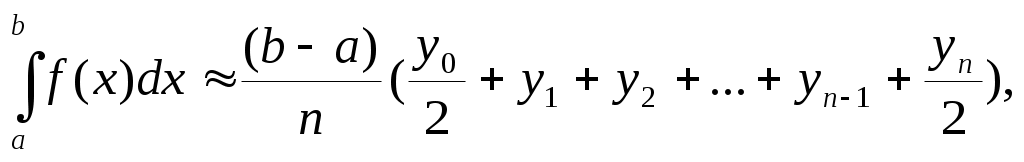
эта формула называется общей формулой трапеций ее можно переписать в следующем виде:
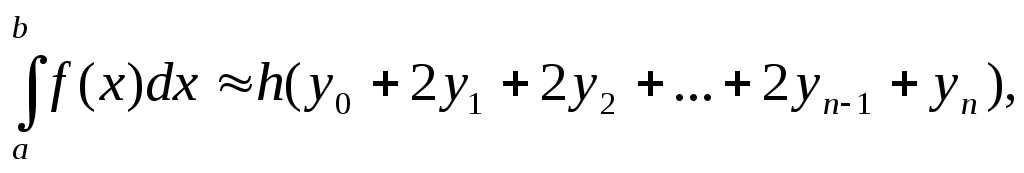
где шаг h = (b-a)/n .
Метод Симпсона (парабол)
Точность приближенного возрастает, если подинтегральную функцию y = f(x) на отрезке [a,b] интерполировать участками парабол, то в этом случае используется метод Симпсона. Для увеличения точности вычислений отрезок [a,b]на n пар участков [x2n-2, x2n-1, x2n]. Вычисление определенного интеграла проводится по формуле:
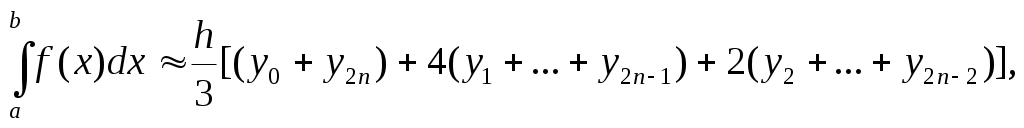
где h=(b-a)/2n
В работе используете три варианта вычисления определенного интеграла, для этого используете следующие элементы управления: 3 переключателя, кнопку – вычислить, счетчик и поле для ввода n – число интервалов, поле – значение x.
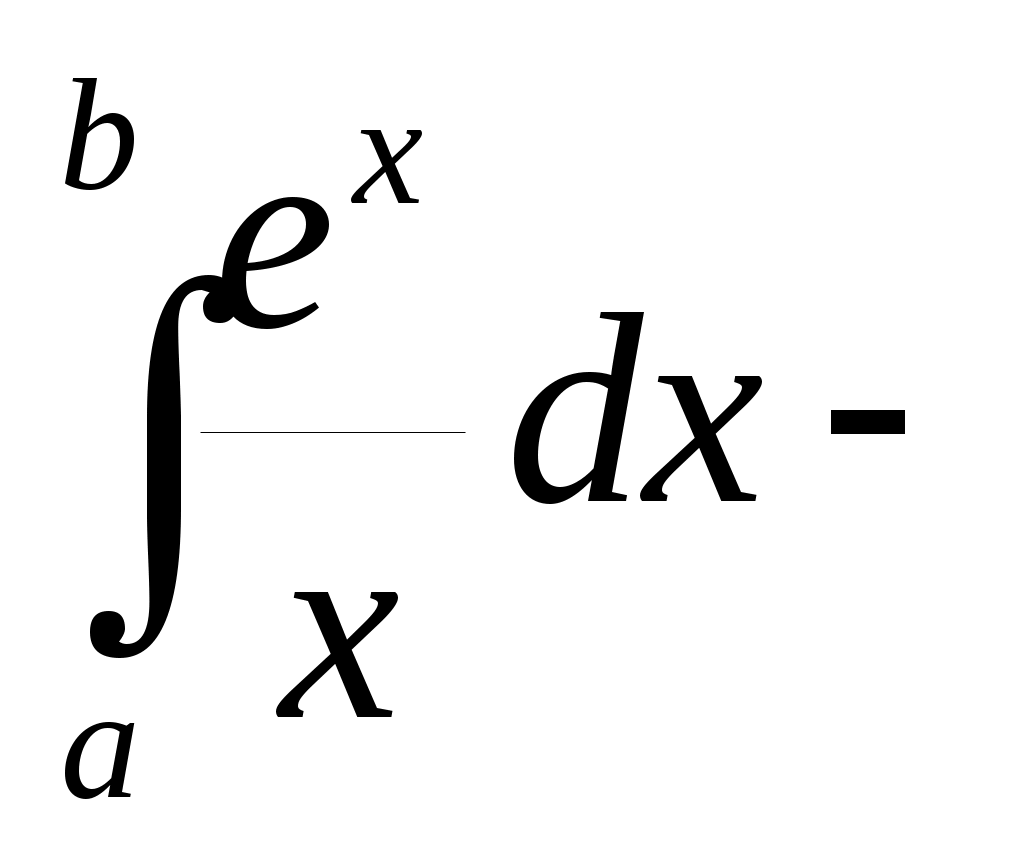
Метод прямоугольников,
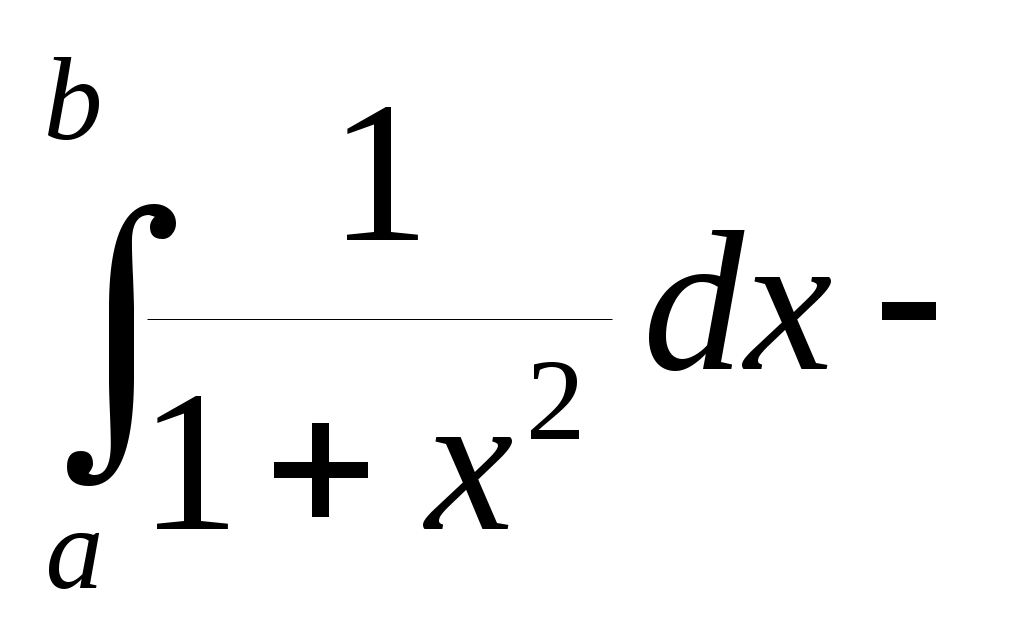
метод трапеций , Симпсона
Решение нелинейных уравнений
Необходимость отыскания корней нелинейных уравнений встречается при расчетах линейных систем автоматического уравнения, собственных колебаний машин и конструкций со многими степенями свободы и т. д. Основная форма записи этих уравнений F(x)=0 .
Имеются две разновидности нелинейных уравнений: алгебраические и трансцендентные.
Алгебраические уравнения n-ой степени A0xn+A1xn-1+…+An=0 имеют n корней, коэффициенты Ai могут быть как действительными, так и комплексными числами.
Трансцендентные уравнения содержат степенные, тригонометрические, экспоненциальные и другие функции от некоторого аргумента x, например, e-x+sinx = 0 . Такие уравнения обычно имеют бесконечное множество корней.
Поиск корней нелинейного уравнения состоит из трех этапов: определение границ существования корней, отделение корней и уточнение корней.
|
|
|
Скачать 0.95 Mb.