VBA-методичка. Практикум по информатике для студентов очной формы обучения Часть ii. Visual Basic for Applications
 Скачать 0.95 Mb. Скачать 0.95 Mb.
|
Разработка приложения “Решение системы линейных уравнений”Взять за основу модуль, созданный в лабораторной работе 3. Модуль должен содержать следующие общие процедуры: MNTab - определение M, N - размерности матрицы, TabCXCY - копирование идентификаторов столбцов и строк в массивы CX, CY, TabA - копирование матрицы с листа Excel в массив A, XAI (I) - вычисление скалярного произведения вектора x на вектор aI (функция) с записью результата в I-ю ячейку первого столбца на листе Excel, Jordan - шаг жорданова исключения (процедура поясняется ниже) – преобразование всей матрицы A с записью новых значений ее элементов в таблицу на листе Excel, обращение к процедуре TabA, перемена местами элементов CX и CY с записью значений и в ячейки Excel, копирование матрицы с листа Excel в массив A. Разместить на листе Excel командную кнопку BTN1 с надписью (свойство Caption) Решение системы уравнений. В событийную процедуру BTN1_Click включить: определение M, N, вывод сообщения и завершение работы, если M не равно N; переопределение размерности массивов CX, CY, A и копирование в них содержимого соответствующих ячеек листа Excel; выполнение шага жорданова исключения N раз (r – номер диагонального элемента матрицы, называемого разрешающим; с ним выполняется шаг жорданова исключения); перед обращением к процедуре Jordan надо проверять, не равен ли нулю элемент матрицы A(r,r) – этот фрагмент программы можно записать так For r = 1 To N If Abs(A(r, r)) < 0.00000001 Then MsgBox "Матрица содержит линейно зависимые строки (столбцы)": Exit Sub End If Jordan r Next r (проверка на нуль в программах выполняется с учетом точности вычислений); вычисление каждого значения Xi (i=1,…,N) путем умножения вектора y на вектор Ai с использованием функции XAI; заметим, что после того, как были выполнены N шагов жордановых исключений, на месте матрицы A находится обратная матрица A-1, а массивы CX и CY поменялись своим содержимым – в массиве CX теперь хранятся известные значения Yj (j=1,…,N), а в массиве CY (и в первом столбце на листе Excel) – идентификаторы X1,…,XN. Эти идентификаторы и надо заменить вычисленными значениями Xi (i=1,…,N). Поясним алгоритм шага жорданова исключения. В разделе 4 упоминалось, что матрицу A (см. рис. 2) можно рассматривать как таблицу коэффициентов, позволяющих связать любой Yi уравнением со значениями X1 ,…, XN : Yi = x ∙ Ai. Глядя на эту таблицу, над столбиками представим себе значения Xj (вектор-строку x), а левее строк – значения Yi (вектор-столбец y). Один шаг жорданова исключения с разрешающим элементом Arr приводит к тому, что Xr и Yr меняются местами, а вся матрица A изменяется так: разрешающий элемент A(r,r)=1/A(r,r) , элементы разрешающего столбца A(i,r)=A(i,r)/A(r,r) , i=1 ,…, N , элементы разрешающей строки A(r,j)= - A(r,j)/A(r,r), j=1 ,…, N , прочие элементы A(i,j) = ( A(i,j) ∙ A(r,r) – A(i,r) ∙ A(r,j) ) / A(r,r) . После того, как будут выполнены N шагов жордановых исключений, вектор y окажется наверху (над матрицей), а вектор x – слева от матрицы. Сама матрица к этому моменту будет обращена – теперь она содержит коэффициенты, позволяющие вычислять значения Xi , если известны значения Yj : X(i)= y ∙ Ai. Приложение надо отладить на примерах. Подготовить примеры совсем не трудно. Представим себе, что N=3, а значения элементов вектора x известны, например: x={1,2,3}. Теперь, задавшись матрицей A, например, A={11,13,13; 21,22,24; 30,32,33}, получим y={76, 137, 193}. Неизвестными будем считать значения X1=1, X2=2, X3=3. Их и найдем. Литература к курсовой работе 1. Зуховицкий С.И., Авдеева Л.И. Линейное и выпуклое программирование. М: Наука, 1967. –460 с. 2. Разработка приложения “Статистический анализ данных”Постановку задачи для этого приложения ограничим упрощенным статистическим анализом: вычислением средних значений признаков, стандартов (средне-квадратических отклонений от генерального среднего), матрицы коэффициентов корреляции и матрицы стандартов коэффициентов корреляции. Поясним эту задачу, обратившись к матрице на рис. 10.5. Теперь матрицу будем рассматривать не как таблицу коэффициентов, связывающих зависимые переменные y={Y1,…,YN} c независимыми переменными x={X1,…,XN} (см. предыдущую работу), а как таблицу объекты-свойства. Соответственно, в первом столбце листа Excel разместим идентификаторы объектов (например, их номера: 1 ,…, M), а в первой строке – идентификаторы свойств (например, X1 ,…, XN). Одна строка матрицы содержит значения свойств одного объекта, а один столбец – значения одного свойства для всех объектов. Таблицы объекты-свойства часто применяются в различных предметных областях. Например, в геологии при поисках и разведке полезных ископаемых отбирают из массива горных пород M проб, а в каждой пробе химическими или физическими методами определяют содержания N компонентов (обычно M>N). По этим анализам судят о массиве горной породы. Аналогично тестируют продукцию металлургического комбината – выборочно отбирают образцы и подвергают их анализам на содержание железа, серы и других элементов. Статистически обработав результаты анализов образцов, судят о качестве целой партии продукции. Здесь важно понять, что в подобных ситуациях практически невозможно проанализировать весь массив горных пород или всю партию продукции - как говорят статистики, всю генеральную совокупность. Поэтому в таблицу объекты-свойства включают результаты анализов (измерений) для выборки из генеральной совокупности. По этой выборке находят средние значения Xjo каждого признака, характеризующие центр рассеяния значений признака и коэффициенты ковариации Sjk, характеризующие меру и форму рассеяния: 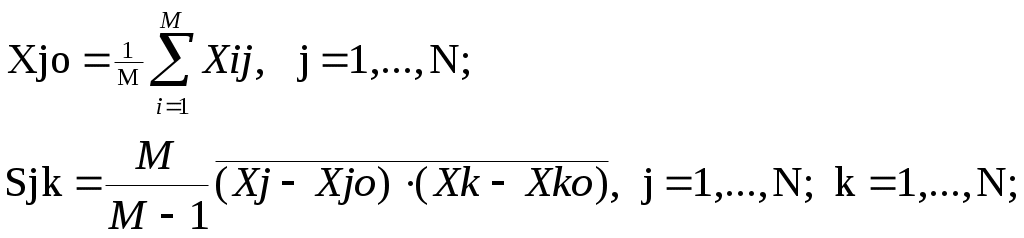 Коэффициент ковариации Sjk вычисляется так: берутся два столбца матрицы с номерами j и k , затем суммируются произведения отклонений i-ых элементов этих столбцов от своих средних, и накопленная сумма делится на M, полученное среднее значение произведения отклонений умножается на поправочный коэффициент M / (M-1). Этот коэффициент компенсирует занижение коэффициентов ковариации, которое произошло, т.к. вместо неизвестных генеральных средних в формуле использованы выборочные средние значения признаков. Рассчитанную матрицу коэффициентов ковариации можно разместить на листе 2 книги Excel – так же, как на листе 1 размещена исходная матрица (см. рис. 10.5), только размерность ковариационной матрицы не M ∙ N , а N ∙ N , и идентификаторами строк и столбцов являются идентификаторы признаков (свойств) объектов. Средние значения надо разместить на листе 1 под соответствующими столбцами исходной матрицы, но пропустив одну строку. На листе 1 надо также разместить командную кнопку BTNSTAT с надписью (свойство Caption) Расчет статистик. В начало событийной процедуры BTNSTAT_Click надо включить определение M, N, копирование в массив CX идентификаторов признаков, а в двумерный массив A – матрицы (см. предыдущую работу и модуль, приведенный в подразделе 10.4 после рис. 10.5). После копирования данных в массивы, запрограммируйте вычисление средних значений признаков и матрицы ковариаций. Диагональные элементы ковариационной матрицы называются дисперсиями. Корни квадратные из дисперсий Sjj называются стандартами sj, или средне-квадратическими отклонениями значений признаков от генеральных средних (от математических ожиданий значений признаков). Стандарты надо вычислить и разместить на листе Excel под средними значениями. Часто между признаками наблюдаются связи: при переходе от объекта к объекту мы видим, что увеличение признака j , как правило, сопровождается увеличением признака k – это положительная корреляция. Если же при увеличении значения Xj значение Xk, как правило, уменьшается, то это корреляция отрицательная. Близость связи между двумя признаками j и k к линейной оценивается коэффициентом парной корреляции: rjk = Sjk / (sj ∙ sk) , j=1,…, N, k=1,…, N. Матрицу коэффициентов корреляции можно разместить на месте ковариационной матрицы, нормируя ее элементы на стандарты. Значения коэффициентов парной корреляции должны принадлежать интервалу [-1, 1 ]. Достоверность, или, как говорят статистики, значимость коэффициентов корреляции зависит от объема выборки. Если в выборку включить малое число проб, а рассеяние значений Xj и Xk велико, то коэффициент корреляции случайно может получиться большим или малым. Чтобы оценить значимость коэффициентов парной корреляции, вычисляют их стандарты: s(rjk) = ( 1- r2jk ) / Матрицу стандартов коэффициентов парной корреляции можно разместить на листе 3 книги Excel. С некоторым приближением о значимости коэффициентов корреляции судят так: если │ rjk │< s(rjk) , то корреляцию нельзя считать значимой. При разработке рассматриваемого приложения наиболее трудным этапом является программирование вычисления коэффициента ковариации. Это вычисление целесообразно локализовать в функции Function SJK ( j As Integer, k As Integer) As Double К этой функции необходимо обратиться N∙N раз : цикл по j от 1 до N, а при каждом j цикл по k от 1 до N. Методы статистического анализа данных полезно знать каждому специалисту. Эта курсовая работа знакомит с началами статистического анализа. Любознательные студенты могут, обратившись к литературе, расширить свои знания в этой области, а при желании – и само разработанное приложение, включив в него, например, вычисление коэффициентов асимметрии и эксцесса для каждого признака, коэффициентов уравнения регрессии, связывающего первый признак с остальными, и т.п. Литература к курсовой работе 2. Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. М.: Наука, 1968. –720 с. Шор Я. Статистистические методы анализа и контроля качества и надежности. М.: Советское радио, 1962. –552 с. Ломтадзе В.В. Программное и информационное обеспечение геофизических исследований. М.: Недра, 1993. –268 с. Разработка приложения “Решение треугольника” Пусть имеется треугольник ABC с углами A,B,C и длинами противолежащих углам сторон LA,LB,LC. Разработать приложение, в котором по заданным параметрам треугольника определяются остальные - не заданные. Если исходные данные заданы так, что задачу решить нельзя, то программа должна выводить сообщение с помощью процедуры MsgBox. Рекомендации. Разместить на листе Excel рисунок треугольника с подписями вершин, поля (TextBox) с именами TBA, TBB, TBC, TBLa, TBLb, TBLc и кнопку с заголовком Вычислить. Слева от текстовых полей поместить подписи A,B,C, LA,LB,LC. Событийная процедура, соответствующая командной кнопке, должна проверять каждый параметр (задан ли он) и вычислять (если не задан) по значениям других параметров. Разработка приложения “Определение площади произвольной фигуры” Пусть многоугольник произвольной формы (полигон) задан координатами вершин X,Y в двух столбцах на листе Excel. На этом же листе разместить командную кнопку и поле (TextBox) с именем TBS для вывода значения площади. Слева от поля TBS поместить надпись Площадь полигона. Вычисление площади целесообразно локализовать в подпрограмме-функции вида Function Spoligon(M As Integer, X() As Single, Y() As Single) As Single Dim i As Integer, x1 As Single, y1 As Single, S As Single { Вычисление S } End Function Функция может содержать следующие блоки: S=0, x1 = X(1), y1 = Y(1), i=2 S = S + (y1 * (X(i) - X(i + 1)) + Y(i) * (X(i + 1) - x1) + Y(i + 1) * (x1 - X(i))) / 2 i=i+1, передача управления блоку 2, если i Spoligon = Abs(S) Разработка приложений “Графические построения в плоскости XOY” Различные графические построения часто необходимы в любой практической деятельности. В литературе по VBA этот вопрос практически не освещен, но в Excel и в Word всегда можно вызвать на экран панель инструментов Рисование и конструировать рисунок, включая в него линии, надписи и другие фигуры, образцы которых (Shapes) представлены на панели инструментов Рисование. Если перед созданием рисунка включить запись макроса (кнопка Записать макрос на панели инструментов Visual Basic), а затем в окне Visual Basic посмотреть его текст и, кроме того, обратиться к встроенной справке, то становится ясно, как программировать векторную графику в VBA. Именно так мы и поступили. Далее приводится начало модуля, содержащего базовые процедуры, с помощью которых можно программировать графические построения на плоскости XOY. ' Глобальные переменные и константы Dim cx As Single, cy As Single ' cx,cy - масштабные коэффициенты: пиксели/сантиметры Dim nx1 As Integer, ny1 As Integer, nx2 As Integer, ny2 As Integer Dim RedClr As Integer, GreenClr As Integer, BlueClr As Integer Dim FntName As String, FntSize As Integer, FntColor As Integer Const nx0 As Integer = 25.5: Const ny0 As Integer = 25.5: ' Инициализация графического окна размером Lx ∙ Ly (в сантиметрах) ' Начало координат в левом верхнем углу окна, ось X направлена вправо, Y- вниз Sub GrIni() SP 0, 0, 0 cx = TextBoxCX.Value: cy = TextBoxCY.Value Lx = TextBoxLX.Value: Ly = TextBoxLY.Value Лист2.Activate: Лист2.Shapes.SelectAll Selection.Delete ' Удаление графических элементов с листа 2 Лист2.Shapes.AddShape(msoShapeRectangle, nx0, ny0, Lx * cx, Ly * cy).Select End Sub ' Пересчет координат из сантиметров чертежа в пиксели (точки) Function GETnx(xcm As Single) As Integer GETnx = nx0 + xcm * cx End Function Function GETny(ycm As Single) As Integer GETny = ny0 + ycm * cy End Function ' Перемещение в точку xcm, ycm (Move Absolute, координаты точки - в см) Sub MA(xcm As Single, ycm As Single) nx1 = GETnx(xcm): ny1 = GETny(ycm) End Sub ' Вычерчивание линии из текущей точки в точку xcm, ycm (Plot Absolute) Sub PA(xcm As Single, ycm As Single) nx2 = GETnx(xcm): ny2 = GETny(ycm) With Лист2.Shapes.AddLine(nx1, ny1, nx2, ny2).Line .ForeColor.RGB = RGB(RedClr, GreenClr, BlueClr) End With nx1 = nx2: ny1 = ny2 End Sub ' Установка цвета линий (Set Pen) Sub SP(Red As Integer, Green As Integer, Blue As Integer) RedClr = Red: GreenClr = Green: BlueClr = Blue End Sub ' Установка шрифта, его размера и цвета (Set Font) ' Цвет: 1-черный, 2-пусто, 3-красный, 4- ярко-зеленый, 5-синий, ' 6-желтый, 7-светло-фиол., 8-голубой, 9-коричн., 10-зеленый, 11-темно-синий Sub SF(Name As String, Size As Integer, Color As Integer) FntName = Name: FntSize = Size: FntColor = Color End Sub ' Надпись (Write String) – указываются размеры текстового окна и сам текст Sub WS(xcm As Single, ycm As Single, Lxcm As Single, Lycm As Single, _ Txt As String) Лист2.Shapes.AddTextbox(msoTextOrientationHorizontal, _ GETnx(xcm), GETny(ycm), Lxcm * cx, Lycm * cy).Select Selection.ShapeRange.Line.Visible = msoFalse Selection.Characters.Text = Txt With Selection.Characters(Start:=1, Length:=Len(Txt)).Font .Name = FntName .Size = FntSize .ColorIndex = FntColor End With End Sub ' Значок (1-восьмиугольник, 2-звездочка, 3-треугольник) Private Sub SignN(xcm As Single, ycm As Single, _ Lxcm As Single, Lycm As Single, NS As Integer) If NS = 1 Then Worksheets(2).Shapes.AddShape(msoShapeOctagon, _ GETnx(xcm), GETny(ycm), Lxcm * cx, Lycm * cy).Select If NS = 2 Then Worksheets(2).Shapes.AddShape(msoShape5pointStar, _ GETnx(xcm), GETny(ycm), Lxcm * cx, Lycm * cy).Select If NS = 3 Then Worksheets(2).Shapes.AddShape _ (msoShapeIsoscelesTriangle, GETnx(xcm), GETny(ycm), Lxcm * cx, Lycm * cy).Select End Sub Private Sub Btn1_Click() ' Пример событийной процедуры GrIni MA 5, 5 PA 10, 5 SP 200, 0, 0 PA 10, 10 SF "Times New Roman Cyr", 9, 11 WS -0.8, -0.2, 0.8, 0.4, "0.0" End Sub Предлагаемые процедуры разработаны нами, чтобы избежать непосредственного использования конструкций VBA, позволяющих размещать на листе книги Excel линии и надписи, поскольку синтаксис этих конструкций довольно сложен. Приведенный в конце модуля пример простейшей событийной процедуры показывает, как используя процедуры GrIni, MA, PA, SP, SF, WS, программировать построение графиков, схем, чертежей и т.п. Набор перечисленных процедур расчитан на то, что на листе 1 книги Excel размещены поля TextBoxLX, TextBoxLY, TextBoxCX, TextBoxCY и командная кнопка Btn1.  Lx 16 Ly 16 27 cx Построить график 29 cy В полях редактирования (TextBox) задаются размеры чертежа в см и масштабные коэффициенты для перехода от см к точкам (пикселям). Коэффициенты cx, cy можно скорректировать после вывода чертежа на принтер. Процедура GrIni должна использоваться первой – она вычерчивает прямоугольное окно размером Lx∙Ly на листе 2 книги Excel. В этом окне затем проводятся дальнейшие построения. Остальные процедуры легко понять по распечатке. Теперь сформулируем варианты курсовой работы. Вариант 1. На листе 1 разместить элементы управления и в двух столбцах - значения X, Y. На листе 2 построить график Y(X). При построении координатных осей найти диапазоны изменения X, Y; оси оцифровать «круглыми» значениями. Вариант 2. Аналогичен варианту 1, но надо строить график X(Y). Вариант 3. Построить разными цветами графики F1(X), F2(X), разместив на листе 1 три ряда (столбца) чисел: X, F1, F2. Оба графика построить в одном и том же масштабе. Вариант 4. Построить многоугольник (полигон) заданный координатами вершин X,Y в двух столбцах на листе Excel. Считать, что ось X направлена вверх (как принято в геодезии). Построить оси координат, оцифровав их "круглыми" значениями, нанести многоугольник, подписать порядковые номера точек. Разработка приложения “Вычисление определенного интеграла” Инженеру часто приходится вычислять значение определенного интеграла численными методами. Это бывает в тех случаях, когда либо не удается выразить интеграл в замкнутой форме, либо она настолько сложна , что проще воспользоваться численным интегрированием. Например, при проверке правильности выбора мощности двигателя по графику переходного процесса по току I(t) требуется в интервале от 0 до конечного времени работы tp вычислить tp интеграл t2(t)dt . Этот интеграл при произвольной кривой тока удобнее всего 0 вычислять численными методами параллельно с поиском решения дифференциальных уравнений, описывающих поведение системы электропривода. В Геометрический смысл определенного интеграла F(x)dx – это площадь А фигуры, ограниченной ординатами А и В, осью абцисс и графиком подинтегральной функции F(x) . Широко известными методами, использующими для приближенного подсчета определенных интегралов их замену конечной суммой, являются методы прямоугольников, трапеций, парабол (Симпсона). Интегрирование по методу прямоугольников Метод прямоугольников основан на непосредственном определении интеграла: n → ∞ где Вычисление определенного интеграла геометрически сводится к вычислению площади криволинейной трапеции, ограниченной Если точку ξi совместить с левым концом отрезка Δxi , то приближенное значение интеграла равно площади фигуры и может быть представлено формулой левых прямоугольников: |
