шпорки готовые логика не всё. Предмет и значение логики. Логика и право
 Скачать 426 Kb.
|
|
15.Объединенная классификация простых категорических суждений по качеству и количеству. в логике существует объединенная классификация суждений по их качеству и количеству. Возможны 4 вида таких суждений: А, I, E, O. А – суждения по количеству (т.е. по объему S) общие, а по качеству (т.е. по характеру связки) утвердительные. «Все рецидивисты – преступники», схема данного суждения – «Все S суть Р». Существуют и общевыделяющие суждения «Только бессмертные живут вечно» - «Все S, и только S, суть Р». I – частные по количеству, утвердительные по качеству. «Некоторые свидетели дают верные показания» - «Некоторые S суть Р». Частновыделяющие – «Некоторые художники, и только они, живописцы», «Некоторые S, и только S, суть Р». E – общие по количеству, отрицательные по качеству. «Ни один вражеский солдат не остался в живых» - «Ни одно S не есть Р». O – частные по количеству, отрицательные по качеству. «Некоторые свидетели не дают верных показаний» - «Некоторые S не суть Р». «Affirmo» (утверждаю), «Nego» (отрицаю)Эта классификация достаточно часто используется в логике; особое значение здесь имеет следующий момент: распределены термины (т.е. субъект и предикат) в них или нет. Распределённым считается термин, мыслимый во всем объеме, нераспределённым – если он мыслится лишь частично, т.е. подразумеваются не все предметы, составляющие объём данного понятия. А: Все S суть Р – S распределен, а Р – нет. Например: «Все курсанты нашего факультета остались живы после эпидемии».   S – распределен, он взят в полном объеме, речь идет обо всех студентах нашего факультетаS P само кванторное слово указывает на распределенность S. Р – нераспределен, т.к. в нем мыслится только часть лиц, оставшихся в живых после эпидемии, а именно, - курсанты нашего факультета. За исключением случаев, когда суждение – общевыделяющее. Например: «Только люди – разумные существа на Земле». В общевыделяющих суждениях субъект и предикат является равнообъемными понятиями (словами синонимами).  S P Здесь распределены не только S, но и Р. I: «Некоторые S суть Р» - S и Р нераспределены. Например: «Некоторые курсанты нашего потока – спортсмены». S – нераспределен т.к. в нем мыслится только часть курсантов потока. Само кванторное слово указывает на нераспределенность S. Объем S лишь частично включается в объем Р. Только некоторые курсанты нашего потока относятся к числу спортсменов. И объем Р лишь частично включается в объем S. Имеются в виду S Р не все спортсмены, а лишь те, которые являются курсантами нашего потока. И  ная картина прослеживается при анализе частновыделяющих суждений. Имеем суждение I «Некоторые S, и только S, суть Р» - «Некоторые геометрические фигуры, и только они, являются треугольниками. Здесь S нераспределен, а Р распределен, ибо в нем мыслятся все треугольники, которые являются геометрическими фигурами.Р S E: «Ни одно S не есть Р», S и Р распределены. Например: «Ни один студент нашей группы не имеет судимости». И S и Р взяты в S Р полном объёме. Объем одного термина полностью исключается из объема другого термина: ни один студент нашей группы не входит в число судимых, и ни один судимый не является студентом нашей группы. Оба термина распределены, в данном случае они несовместимы. O: «Некоторые S не суть Р», S не распределен, Р распределен. Например: Некоторые животные нашего леса – не являются медведями. S не распределен, S Р мыслится лишь часть животных нашего леса, а Р распределен, здесь мыслятся все медведи, ни один из которых не включается в ту часть животных нашего леса, которая мыслится в S. Оказывается, что выделяющими могут быть и суждения О (частноотрицательные) «Некоторые S, и только S, не суть Р» - «Некоторые орденоносцы, и только они, не являются ковалерами ордена Красной Звезды». Субъект нераспределен, предикат распределен.Р S Все это необходимо знать для правильного преобразования суждений и для проверки правильности дедуктивных умозаключений, например, силлогизма. Различают виды суждений и по характеру Р. По характеру Р все суждения делятся на: атрибутивные, реляционные и экзистенциальные. Атрибутивныесуждения раскрывают наличие или отсутствие у предмета мысли тех или иных свойств или признаков. «В. Ульянов-Ленин был сообразительным человеком». Реляционные суждения или суждения об отношениях фиксируют наличие или отсутствие у предмета мысли того или иного отношения к другому предмету. «х R y», x и y – предметы мысли, R – отношение между ними. «Плеханов старше своего друга Мартова»; «Минск севернее Киева», «Москва меньше Мехико». Две разновидности: а) суждения об отношениях между двумя предметами «Москва меньше Мехико». б) суждения об отношениях между тремя и более предметами: «Большая Мурта находится между Енисейском и Абаканом. Итак, суждение с двухместным отношением обычно записывают в виде формулы х R y, где х называют предшествующим членом, а y – последующим членом отношения R. Различают прямое и обратное отношение или конверсию отношений. Отношение, зафиксированное в некотором реляционном суждении, можно изменить таким образом, что предшествующий член станет последующим, и наоборот; «9 меньше 100» - «100 больше 9»; Марк Твен (Сэмьюэл Клеменс) родился в городе Хэннибал» - «Городок Хэннибал – родина Марка Твена» и т.п. Эта операция основана на подборе некоего отношения R1, обратного отношению R. Дело в том, что существует целый ряд пар двухместных предикатов такого рода: «выше – ниже», «старше – младше», «больше – меньше», «муж – жена», «дальше – ближе» и т.д. Суждения, основанные на взаимной конверсии отношений синонимичны, и соответственно, взаимозаменяемы. «Детройт расположен восточнее Портленда» - «Портленд расположен западнее Детройта»; «Казбек ниже Эвереста» - «Эверест выше Казбека».Кроме того существуют симметричные, асимметричные и несимметричные отношения. Симметричные: хRy → yRx, т.е. например, «Петров – родственник Сидорова», «(2+4) = (1+5)», «Пущин – современник Пушкина». Переставить местами x и y, и истинность суждения, как его смысл сохранится. Асимметричные: xRy → не –yRx, т.е. например, «Александр III – отец Николая II» → «Неверно, что Николай II – отец Александра III»; «100 больше 10» → «Неверно, что 10 больше 100». Несимметричные: из суждения хRy не следуют с необходимостью ни структура yRx, ни структура не–yRx. Имеем суждение «Михаил – завистник Виталия», из него нельзя с необходимостью сделать вывод ни о том, что Виталий завидует Михаилу, ни о том, что он ему не завидует. Экзистенциальные суждения или суждения существования (чего-либо) фиксируют наличие или отсутствие самого предмета мысли. Р здесь выражается словами «существует (не существует)», «есть (нет)», «был (не был)» и др. «Государства под названием Техас не существует с 1845 года». «Пост Президент Франции установлен в 19 веке». «Инопланетяне существуют». «Чертей нет на белом свете». Экзистенциальные и реляционные суждения целесообразно рассматривать как частный случай атрибутивных суждений, ибо и экзистенциальное суждение, и реляционное можно выразить в форме атрибутивного. «Солнце существует» означает, что «солнце обладает свойством существовать». Хотя, естественно, последнее суждение является искусственной конструкцией. Суждения с отношением (реляционные суждения). Виды этих суждений таковы: 1. Прямые и обратные суждения. Об отношениях между двумя понятиями можно составить суждение, сделав одно из них субъектом, а другое предикатом, а затем поменяв их местами (ролями). Если при этом смысл суждения не исказится, оба эти суждения являются по отношению друг к другу прямым и обратным. Операция же перемены мест субъекта и предиката в таких суждениях называется конверсией. Пример прямого и обратного суждений: «Сумма действительного и мнимого чисел (S) называется комплексным числом (Р)». В результате конверсии имеем: «Комплексным числом (Р) называется сумма действительных и мнимых чисел (S)». 2. В некоторых реляционных суждениях два понятия можно переводить из субъекта в предикат и из предиката в субъект без ущерба для истинности суждений. Например: «От города А (S) до города В 100 км (Р)» и «От города В (S) до города А 100 км (Р)». Такие суждения называются симметричными. Несимметричными называются суждения, в которых подобная перестановка невозможна. Например: «Эйлер жил раньше Гаусса». Несимметричными называют также суждения, в которых такая перестановка не позволяет сделать какой-либо вывод без получения дополнительной информации. Например: «Я вас очень уважаю». А вы меня? Из того, что я вас уважаю, не следует вывод о том, как вы ко мне относитесь. 3. Транзитивные суждения. Транзитивность — это отношения по принципу: а = b, b = с, а = с. Например: «Иванов — хороший токарь». «У токарей хороший глазомер». «Иванов имеет хороший глазомер». Это суждения транзитивные. 5. Категорические суждения. Слово «категорический» означает «ясный, безусловный, не допускающий двух толкований». Суждение, в котором отрицание или утверждение делается в категорической форме, называется категорическим. Такие суждения наиболее удобны для изучения, потому они и изучены хорошо. Категорическим суждениям присущи две характеристики — качество и количество. «Качеством суждения называется его утвердительная или от- рицательная форма»'. Если мы утверждаем, что признак Р присущ S, это утвердительное суждение: «Папоротники — споровые растения». Если же мы отрицаем это, то суждение отрицательное: «Венгерский язык не относится к индоевропейским языкам». Если объемы S и Р совпадают или S включено в Р, суждения о принадлежности Р к S могут быть только положительными. Если эти объемы несовместимы, суждения могут быть только отрицательными. Если объемы пересекаются или Р включено в S, то суждения эти могут быть как положительными, так и отрицательными, в зависимости от того, в какую часть S мы помещаем тот конкретный предмет, относительно которого строится суждение (в ту часть, которая является для S и Р общей, или в ту, которая входит в S, но не входит в Р). Количество показывает нам, к чему относится утверждение или отрицание, ко всему объему S или только к его части. Выражается это словами «все» или «некоторые» и им равнозначными. Если речь идет об отрицании, то «все» может заменяться словами «ни один», «никакой» и т. п. С точки зрения количества суждения делятся на общие, в которых что-то утверждается или отрицается обо всем объеме S («Все — суета сует»), и частные, в которых что-то утверждается или отрицается о части объема S («Некоторые люди увлекаются дельтапланеризмом»). В частные включаются также и единичные суждения («День 1 января — новогодний праздник»). 16.Распределенность терминов в простых категорических суждениях. В логических операциях с суждениями возникает необходимость' установить, распределены или не распределены его термины — субъект и предикат. Термин считается распределенным, если он взят в полном объеме. Термин считается нераспределенным, если он взят в части объема. Рассмотрим, как распределены термины в суждениях А, Е, I, О. Суждение А (Все S суть Р). «Все студенты нашей группы (S) сдали экзамены (Р)». Субъект этого суждения («студенты нашей группы») распределен, он взят в полном объеме: речь идет обо всех студентах нашей группы. Предикат этого суждения не распределен, так как в нем мыслится только часть лиц, сдавших экзамены, совпадающая со студентами нашей группы. 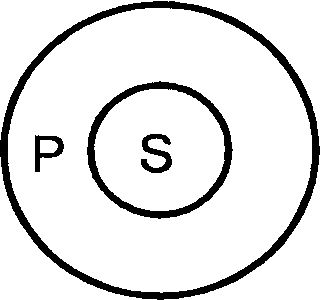 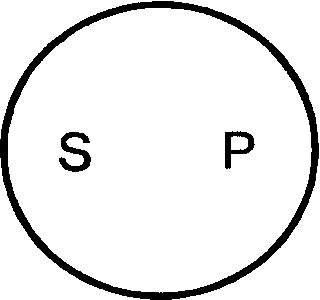 Таким образом, в общеутвердительных суждениях S распределен, а Р не распределен. Однако в общеутвердительных суждениях, субъект и предикат которых имеют одинаковый объем, распределен не только субъект, но и предикат. К таким суждениям относятся общевыделяющие суждения, а также определения, подчиняющиеся правилу соразмерности. Суждение Е (Ни одно S не есть Р). «Ни один студент нашей группы (S) не является неуспевающим (Р)». И субъект, и предикат взяты в полном объеме. Объем одного термина полностью исключается из объема другого: ни один студент нашей группы не входит в число неуспевающих, и ни один неуспевающий не является студентом нашей группы. Следовательно, в общеотрицательных суждениях и S, и Р распределены. 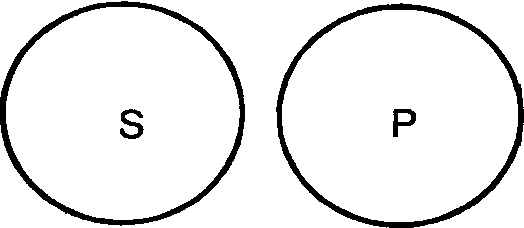 Суждение I (Некоторые S суть Р). «Некоторые студенты нашей группы (S) — отличники (Р)». Субъект этого суждения не распределен, так как в нем мыслится только часть студентов нашей группы, объем субъекта лишь частично включается в объем предиката:только некоторые студенты нашей группы относятся к числу отличников. Но и объем предиката лишь частично включается в объем субъекта: не все, а только некоторые отличники — студенты нашей группы. Следовательно, в частноутвердительном суждении ни S, ни Р не распределены. 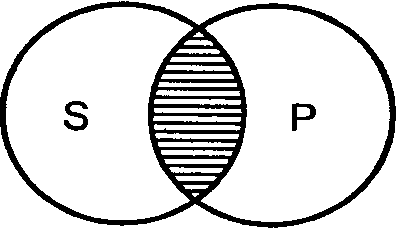 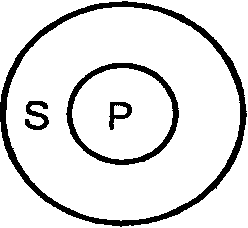 Исключение из этого правила составляют частновыделяющие суждения, предикат которых полностью входит в объем субъекта. Например: «Некоторые родители, и только они (S), являются многодетными (Р)». Здесь понятие «многодетные» полностью входит в объем понятия «родители». Субъект такого суждения не распределен, предикат распределен. Суждение О (некоторые S не суть Р). «Некоторые студенты нашей группы (S) — не отличники (Р)». Субъект этого суждения не распределен (мыслится лишь часть студентов нашей группы), предикат распределен, в нем мыслятся все отличники, ни один из которых не включается в ту часть студентов нашей группы, которая мыслится в субъекте. Следовательно, в частноотрицательном суждении S не распределен, а Р распределен. 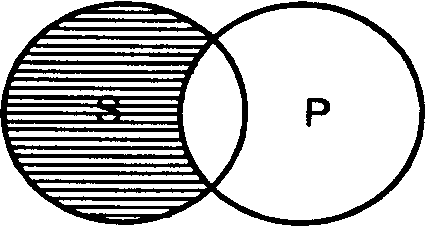 Итак, субъект распределен в общих (А и Е) и не распределен в частных суждениях (I и О). Предикат распределен в отрицательных (Е и О) и не распределен в утвердительных суждениях (А и I). В выделяющих суждениях предикат распределен. 16.Логические отношения между простыми категорическими суждениями. Атрибутивные простые суждения по содержанию делятся на сравнимые и несравнимые. Несравнимые суждения – суждения, имеющие разные S или Р, или то и другое вместе: «Космос безграничен», «Драконовские законы жестоки». Сравнимые суждения обладают одинаковыми S и Р, но могут различаться по качеству и количеству. Они делятся на совместимые и несовместимые. Совместимые суждения содержат одну и туже мысль – полностью или частично. Между ними возникают такие логические отношения: а) эквивалентности, б) подчинения, в) частичной совместимости. а) Эквивалентность (равнозначность) – это отношение между суждениями, у которых S и Р выражены одними и теми же равнозначными понятиями, хотя и разными словами. «Все адвокаты – юристы» - «Все защитники в суде правоведы». Последующие отношения между атрибутивными – A, E, I, O изображаются в виде логического квадрата    А ЕI О б) Подчинение – это отношение между такими суждениями, у которых количество различно, а качество одинаково: A – I, E – O.Закономерности отношения подчинения таковы: - из истинности подчиняющего А или Е, следует, соответственно, истинность подчиненного I или О, но не наоборот. - из ложности подчиненного I или О следует, соответственно, ложность подчиняющего А или Е, но не наоборот. (Если истинно А, «Все адвокаты – юристы, то тем более истинно I»: «Некоторые адвокаты – юристы»). Но если истинно I: «Некоторые свидетели дают верные показания», то отсюда еще не следует, что истинно А: «Все свидетели дают верные показания». В данном случае это ложное суждение. Для других примеров в некоторых случаях А может быть и истинным. в) Частичная совместимость: одинаковое количество, разное качество I - О. Закономерность такова: - оба суждения могут быть одновременно истинными, но не могут быть одновременно ложными. Истинно I: “Некоторые свидетели правдивы», может оказаться истинным и О: «Некоторые свидетели не являются правдивыми». Имеет место и второй вариант. Истинно I: «Некоторые адвокаты – юристы», но это не значит, что истинно О: «Некоторые адвокаты – не являются юристами», в данном случае О является ложным. Несовместимые суждения. Они бывают двух видов. а) Противоположность: А и Е, одинаковое количество, разное качество. Закономерность такова: - оба суждения не могут быть одновременно истинными, но могут быть одновременно ложными. Т.е. закономерность обратная отношению частичной совместимости. (Если истинно А: «Все адвокаты – юристы», то с необходимостью ложно Е: «Ни один адвокат не юрист», но если ложно А: «Все философы материалисты», то отсюда еще не следует с необходимостью истинность Е: «Ни один философ не материалист». В данном случае последнее суждение ложно. б) Противоречие (контрадикторность) – А - О, Е - I. -Противоречащие суждения не могут быть одновременно истинными и одновременно ложными. Если истинно А: «Все адвокаты – юристы», то ложно О, что «Некоторые адвокаты – не юристы». Если ложно А: «Все свидетели правдивы», то истинно О: «Некоторые свидетели не правдивы». таблица истинности (и) и ложности (л), а также неопределенности (н) простых, категорических суждений А, Е, I, О.
|