шпорки готовые логика не всё. Предмет и значение логики. Логика и право

• Название: Предмет и значение логики. Логика и право
• Анкор: шпорки готовые логика не всё.doc
• Дата: 18.09.2017
• Размер: 426 Kb.
• Имя файла: шпорки готовые логика не всё.doc
• Тип: Документы; #8594
• страница: 7 из 8

33.Условно-разделительные (лемматические) умозаключения.

Это такие умозаключения, в которых большая посылка состоит из двух или большего числа условных суждений, а меньшая состоит из разделительного.Здесь мы различаем следующие четыре формы умозаключений:

1. Простой модус ponens, или конструктивный. Он называется ponens потому, что меньшая посылка утвердительная; конструктивным он называется потому, что заключение утвердительное. Его схема:

Если А есть В, то С есть D;

Если Е есть F, то С есть D.

Но или А есть В, или Е есть F.

Следовательно, С есть D.

Пример:Если наука сообщает полезные факты, то она заслуживает внимания. Если изучение науки служит упражнением для умственных способностей, то она также заслуживает внимания. Но каждая наука или сообщает полезные факты, или занятие ею упражняет умственные способности.Следовательно, каждая наука заслуживает внимания.

Заметим, что в этой форме умозаключения в меньшей посылке Утверждаются основания.От этого простого модуса сложный отличается тем, что в нём в условных суждениях нет одного общего основания или общего следствия, как это мы имеем в простом модусе, и самое заключение выражается при помощи разделительного суждения;

2. Сложный модус ponens, или конструктивный. Его схема:

Если А есть B, то С есть D;

И если Е есть F, то G есть Н.

Но или А есть В. или D есть F.

Следовательно, или С есть D, или G есть H.

Пример:Если я брошусь из окна, то я получу ушибы.Если я пойду по лестнице, то я сгорю.Но я должен или броситься из окна, или пойти по лестнице.Следовательно, я или ушибусь, или сгорю.

Заметим, что в этой форме умозаключения в меньшей посылке также утверждается основание.

3. Простой модус tollens, или деструктивный:

Если А есть В, то С есть D:

и если А есть В, то Е есть F.

Но С не есть D и Е не есть F

Следовательно, А не есть В.

Пример:Если бы мы захотели начать войну, то мы должны были бы или сделать заём, или увеличить налоги. Мы не можем сделать ни того, ни другого. Следовательно, мы не можем предпринять войны.

В этой форме силлогизма в меньшей посылке отрицаются бедствия, а потому отрицаются и основания.

4. Сложный модус tollens, или деструктивный.

Если А есть В, то С есть D;

Если Е есть F, то G есть И.

Но С не есть D и G не есть И.

Следовательно, А не есть B и не есть F.

Пример:Лицо, желающее иметь автомобиль, может так рассуждать;

Если бы я был богат, то я автомобиль купил бы.

Если бы я был бесчестен, то я украл бы таковой.

Но я не куплю и не украду.

Следовательно, я не богат и не бесчестен.

Лемматические умозаключения по количеству следствий называются дилеммой, трилеммой и т. д.

Достоверность лемматического умозаключения находится в зависимости от правильности условных суждений в большей посылке и от полноты членов деления в меньшей. Так как эти условия часто не соблюдаются, то лемматическое умозаключение делается•источником ошибок.Источником ошибок является чаще всего неполное перечисление членов деления. Двумя альтернативами иногда нельзя исчерпать всего возможного числа случаев. Весьма часто дилемматическое умозаключение строят таким образом, что из всех возможных альтернатив берут только две альтернативы, вследствие чего и получается ошибка.Пример:Если какой-либо ученик любит учиться, то он не нуждается ни в каком поощрении. Если же он чувствует отвращение к учению, то всякое поощрение окажется бесполезным.Но ученик может или любить учение, или чувствовать к нему отвращение.Следовательно, поощрение или излишне, или бесполезно в деле обучения»

Эта дилемма ложна., потому что «любовь к учению» и «отвращение к учению» не суть единственно возможные альтернативы, так как могут быть" такие ученики, которые не питают любви к учению, но не питают и отвращения к нему; для таких учеников поощрение может быть действительным;

34.Общая характеристика индуктивного умозаключения. Полная индукция.

Индуктивными заключениями называются такие, в которых из единичных или частных суждений выводятся общие суждения.Индукция понимается как метод исследования, целью которого является анализ движения от единичного к общему суждению.

Если посылки исчерпывают весь класс предметов, подлежащих индуктивному обобщению, то индукция называется полной.Если они не исчерпывают всего класса предметов – то индукция считается неполной.Заключением, как по полной, так и по неполной индукции будет общее суждение.

Полная индукция.схема: S1 есть Р,

S2 есть Р,

...

Sп есть Р.

S1, S2, ..., Sп – исчерпывают все предметы класса S.

Следовательно, все S есть Р.

Пример умозаключения по полной индукции:

Сентябрь 1961 года в Красноярске был серым, холодным и дождливым.

Октябрь тоже.

Ноябрь тоже.

Сентябрь, октябрь, ноябрь – осенние месяцы.

Следовательно, осень 1961 года в Красноярске была серой, холодной и дождливой.

Полная индукция - такой вид индуктивного вывода, в котором общий вывод базируется на знании о всех без исключения предметов изучаемого класса, и поэтому заключение здесь - категорическое суждение, причем предикат посылок и заключения, как и вообще во всех индуктивных выводах, один и тот же.

Но в реальном человеческом познании полная индукция занимает все же незначительное место, так как с полным набором случаев человек в силу ограниченности своего существования во времени и пространстве, как правило, не имеет дела, довольствуясь не всеми предметами класса, а лишь частью их. Полная индукция — это умозаключение, в котором на основе принадлежности каждому элементу или каждой части класса определенного признака делают вывод о его принадлежности классу в целом.

Индуктивные умозаключения такого типа применяются лишь в тех случаях, когда имеют дело с закрытыми классами, число элементов в которых является конечным и легко обозримым. Например,число государств в Европе, количество промышленных предприятий в данном регионе, число субъектов федерации в данном государстве и т.п.

Представим, что перед аудиторской комиссией поставлена задача проверить состояние финансовой дисциплины в филиалах конкретного банковского объединения. Известно, что в его состав вхо­дят пять отдельных филиалов. Обычный способ проверки в таких случаях — анализ деятельности каждого из пяти банков. Если окажется, что ни в одном из них не обнаружено финансовых нарушений, то тем самым можно сделать обобщающее заключение: все филиалы банковского объединения соблюдают финансовую дисциплину.

Схема умозаключения полной индукции имеет следующий вид:

Посылки:

1) Si имеет признак Р §2 имеет признак Р

Sn имеет признак Р 2) Si, 82,..., Sn — составляют класс К

Заключение:

Всем предметам класса К присущ признак Р

Выраженная в посылках этого умозаключения информация о каждом элементе или каждой части класса служит показателем полноты исследования и достаточным основанием для логического переноса признака на весь класс. Тем самым вывод в умозаключении полной индукции носит демонстративный характер. Это означает, что при истинности посылок заключение в выводе будет необходимо истинным.

В одних случаях полная индукция дает утвердительные заключения, если в посылках фиксируется наличие определенного признака у каждого элемента или части класса. В других случаях в качестве заключения может выступать отрицательное суждение, если в посылках фиксируется отсутствие определенного признака у всех представителей класса.

Познавательная роль умозаключения полной индукции проявляется в формировании нового знания о классе или роде явлений. Логический перенос признака с отдельных предметов на класс в целом не является простым суммированием. Знание о классе или роде — это обобщение, представляющее собой новую ступень в развитии знания. Так, при выявлении характера кривой, по которой движутся планеты вокруг Солнца, в астрономии первоначально было установлено, что Марс, Венера, Юпитер, Сатурн, Земля обращаются по эллипсообразным орбитам. С открытием новых планет было установлено, что Уран, Нептун, Плутон и Меркурий обращаются по таким же орбитам. В итоге в форме полной индукции было сделано обобщение, что все планеты Солнечной системы обращаются по эллипсообразным орбитам. Это новое знание имеет принципиально иное значение, нежели констатация факта эллипсообразного движения каждой из планет. Во-первых, обобщающий вывод оказывает влияние на развитие понятия «планета Солнечной системы», поскольку в его содержание может быть включен новый признак — обращение вокруг Солнца эллипсообразное. Во-вторых, этот признак может служить основой для выявления других существенных характеристик всего класса явлений, например, для решения вопроса о механизме возникновения планет Солнечной системы.

Демонстративность полной индукции позволяет использовать этот вид умозаключения в доказательном рассуждении. Так, в геометрии теорема о сумме внутренних углов треугольника доказывается отдельно для трех видов треугольников: остроугольных, прямоугольных и тупоугольных. Учитывая, что в каждом из них сумма углов равна 180° и все они составляют конечное множество, строят индуктивное обобщение: во всяком треугольнике сумма его внутренних углов равна 180°.

В судебном исследовании нередко используются доказательные рассуждения в форме полной индукции с отрицательными заключениями. Например, исчерпывающим перечислением разновидностей исключается определенный способ совершения преступления, способ проникновения злоумышленника к месту совершения преступления, тип оружия, которым было нанесено ранение, и т.п.

Применимость полной индукции в рассуждениях определяется практической перечислимостью множества явлений. Если невоз­можно охватить весь класс предметов, то обобщение строится в форме неполной индукции.

35.Структура доказательства.

Доказательство – это аргументация, в которой аргументы являются утверждениями, истинность которых установлена, а формой является демонстративное рассуждение. Итак, различие между аргументацией и доказательством следующее. 1) Аргументация шире доказательства, поскольку здесь применяются как логические, так и внелогические методы и приемы; 2) Аргументируя, мы часто обосновываем не только истинное суждение, но вообще любое суждение использоваться могут при этом любые (сомнительные) суждения в качестве аргументов. Поэтому есть основания считать аргументацию родом, а доказательство и опровержение ее видами.

Видоизменения аргументации с точки зрения ее эпистемических или коммуникативных свойств также могут быть взяты в качестве критериев выделения ее видов. Можно принять во внимание характер аргумента, рассматривая то, что он выражает, можно исходить из специфики демонстрации (формы обоснования). эпистемический подход позволяет выделить в аргументационных процессах аналоги доказательства, опровержения, подтверждения, оспаривания, интеграции. Исходя из коммуникативных свойств, Аристотель выделял три вида «риторических речей»: совещательные, судебные и эпидейктические. По Аристотелю, «дело совещательных – склонять или отклонять, дело судебных – обвинять или оправдывать, дело эпидейктической речи – хвалить или поощрять». Подытоживая приведённую информацию, скажем, что аргументацию в самом общем виде следует разделять на доказательную и недоказательную.

Доказательная аргументация – логическая основа формирования научных убеждений. Задача всякой науки – не только открытие и провозглашение истин, но и их доказательство. Время от времени нужно подвергать проверке устоявшиеся аксиомы и законы. И так в любой сфере деятельности, в том числе и в сфере юриспруденции. В мире существует всеобщая обусловленность предметов и явлений действительности. Ничто не возникает из ничего – все имеет свои основания в других предметах и явлениях. Это и позволяет в мышлении, отражающем действительность, одни мысли основывать на других, обусловливать другими, доказывать их, выстраивать своего рода мыслительную лестницу. Доказательством иногда называют методологическую форму теоретического познания, представляющей собой вывод тезиса из аргументов по определенным правилам того или иного умозаключения. Человек, как известно, существо общественное. Открывая истину, человек хочет поделиться своим открытием с другими. Но для этого он должен убедиться сам в ее истинности, т.е. установить ее необходимую связь с другими истинами, и уже затем убедить в этом других людей. Эта цель и достигается благодаря доказательству. Разве была бы необходимость в доказательстве, если бы все истины носили очевидный характер. Доказательство (в узком смысле) – обоснование истинности тезиса при помощи средств логики и других истинных суждений. Не требуют доказательств: истины факта, получаемые при помощи органов чувств («Дождь закончился»); аксиомы – положения в истинности которых нас убеждает длительная практика человечества.

Многие же истины не столь очевидны и следовательно требуются доказательства. Поэтому-то и существует наука, ибо наука без доказательств невозможна. В доказательстве центр тяжести переносится на то, чтобы установить истинность или ложность того или иного знания, в умозаключении же – на то, чтобы получить новое знание. Правда разграничение, приведенное здесь весьма условно, ибо любое доказательство строится в виде того или иного умозаключения. Доказательству уделяется исключительное внимание в юридической сфере. Существует общая теория права, и частью ее является теория служебных доказательств. Доказывание – стержень судебного процесса. В основу приговора или решения суда кладутся выводы, полученные из анализа явлений, событий, фактов. Приговор или решение должны быть действительно обоснованными, т.е. должны логически вытекать из всего предшествующего разбирательства. Судебная практика имеет великое множество предметов доказательств, это показали еще Демосфен, а затем и Цицерон.

Общая формула доказательства: А_1, А₂, А₃, … А_n → Т. Структура доказательства: тезис; аргументы (доводы, основания); демонстрация (форма или способ доказательства). Тезис – это положение, истинность которого обосновывается посредством данного доказательства. В качестве тезиса могут выступать самые разнообразные суждения, если они не очевидны.

В юридической практике, например, тезис – это факты и обстоятельства подлежащие доказыванию; надо установить: 1) имело ли место событие преступления; 2) виновно ли данное лицо в совершении преступления; 3) степень вины; 4) характер и размеры ущерба; 5) причины и условия совершения преступления.

Большую роль в уголовном расследовании играет доказательство алиби (alibi – в другом месте), нахождение подозреваемого в момент совершения данного преступления в другом месте. Если алиби хотя бы не исключается, то вывод о совершении преступления данным лицом не может быть признан обоснованным. Аргументы – это положения, из которых выводится истинность тезиса. Существуют самые разные виды аргументов: факты, определения, аксиомы. «Юридические факты» – предусмотренные законом обстоятельства, служащие основанием для возникновения или прекращения конкретных правоотношений, также учитываются. Определение раскрывает свойство и признаки предметов и явлений, поэтому, зная одни признаки какого-либо предмета или явления, посредством определения можно вывести и другие свойства и признаки этого предмета или явления. Аксиомы, которые используются в качестве основания доказательств, должны быть системой. Аксиомы не должны противоречить друг другу и не должны зависеть друг от друга. Ранее доказанные положения играют в доказательстве также немалую роль. В некоторых случаях ранее доказанные положения признаются судом. Однако именно в науках они играют решающую роль. На одних ранее доказанных законах выстраиваются другие, как кирпич ставится на кирпич. Так и возводят здание науки в целом, и частных наук, в отдельности. Важно, что один и тот же Тезис можно доказывать при помощи разных аргументов, а один и тот же аргумент нередко используют для доказательства разных тезисов.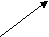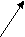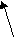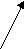

Т Т₁ Т₂

а₁ а₂ а₃ а₄ а₁

По функциональной предназначенности аргументы доказательства классифицируются на основные, исходные и дополнительные. Основными являются аргументы, необходимые и достаточные для исчерпывающего обоснования доказываемого тезиса. Вместе с тем далеко не всегда в процессе интеллектуального взаимодействия основная аргументация полностью приводится в самом начале обсуждения. Иногда это делать нецелесообразно по определенным (часто тактическим соображениям), в большинстве случаев действенным приемом оказывается ограничение начала обсуждения узкими, т.е. исходными аргументами, используя последующие по мере необходимости. Это учитывают, например, при проведении допроса подозреваемого на предварительном следствии.

По происхождению аргументы могут делиться на утверждения о фактах, теоретические источники и ранее доказанные положения. К примеру, в юридическом исследовании утверждения относительно фактов могут иметь форму заключения эксперта по вещественным доказательствам. Все юридические законы и правовые нормы, вовлеченные в рассмотрение обстоятельств дела, представляет собой теоретические источники, общепринимаемые положения, не требующие доказательства. Предварительно проверенные и оцененные в процессуальном порядке свидетельские показания можно рассматривать в качестве ранее доказанных аргументов. Последний элемент доказательства: демонстрация, или форма доказательства. Что бы сформировалось доказательство, нужна последовательная логическая связь, определенное отношение аргументов и тезиса, в этом случае с необходимостью признается истинность или ложность тезиса. Языковыми же средствами доказательства служат выражения «Что и требовалось доказать», «Отсюда следует вывод…» и др.

Виды демонстрации – дедукция, индукция и умозаключение по аналогии. Последнюю хорошо использовать в сочетании с другими способами доказательств. Но когда нет других способов и возможностей обоснования тезиса, то прибегают к аналогии. Что касается тезиса, то не во всех случаях бывает выгодным формулировать его в явном виде. Иногда доказывая, лучше не говорить, что именно доказываешь, а подводить оппонента к своей мысли, чтобы получилось так, будто эта мысль пришла в голову ему самому. Хорошо если оппонент по ходу спора, дискуссии начнет считать эту мысль своей, в этом случае он будет ее придерживаться. (Метод Сократа: Первые вопросы должны быть такими, чтобы оппонент отвечал на них «да» …).Надо сказать, что демонстрация в доказательстве наряду с логическими правилами умозаключения допускает иногда и нелогические способы перехода к обосновываемому тезису – прагматические, психологические, этические, эстетические. На практике процесс доказательства обычно не имеет форму цели чисто логических операций. Здесь интегрируются логические средства, психологические методы, красноречие, которое всегда помогало убедить слушателей.